1 Introduction

Over the past few years, the manganites with the form of Ln1−x A x MnO3 (Ln = trivalent rare earth, A = divalent alkaline earth) have attracted much attention due to their extraordinary magnetic and electronic properties and their promise for the future technological applications [1–3]. A prominent feature of these materials is a insulator–metal transition together with a paramagnetic (PM)–ferromagnetic (FM) transition and a colossal magnetoresistance (CMR) effect, which has been extensively explained in the framework involving a double-exchange model and Jahn–Teller effects [4, 5]. Earlier studies on the critical behaviors around the Curie temperature T C have indicated that critical exponents play important roles in elucidating interaction mechanisms near T C [6]. Critical phenomena in the double exchange (DE) model have been first described within mean-field theory [7]. However, the theoretical calculations based on simplified DE models, reveal that the FM–PM transition in CMR manganites should belong to the Heisenberg universality class [8]. By contrast, the experimental estimates for critical exponents are still controversial including those for short-range Heisenberg interaction [9, 10], the mean-field values [11], and those which cannot be classified into any universality class ever known [12]. Hence, the critical properties of the paramagnetic–ferromagnetic phase transition in manganites pose an important fundamental problem. The aim of this work was to study the effect of Ti-doping La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0 and x=0.05) polycrystalline samples on the structural, magnetic, and the critical parameter.

2 Experimental

In this study, La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (LNPMT) compounds were formed by the standard solid state reaction by mixing 99.994% pure PbCO3, TiO2, MnO2, La2O3, and Nd2O3 powders. The detailed experimental process has been reported elsewhere [13]. The physical properties of every stage were measured. The magnetization properties and the XRD pattern were measured and compared with previous reports to ensure the formation of the same compounds. The structure and phase purity of the prepared samples were checked by X-ray diffraction (XRD), using CuKα 1 radiation at room temperature. The magnetization measurements were carried out by the superconducting interference device (SQUID). For the studies, the isothermal M vs. H is corrected by a standard procedure from low field dc magnetization measurements. In fact, the internal field used for the scaling analysis has been corrected for demagnetization, H=H appl−D a M, where D a is the demagnetization factor obtained from M vs. H measurements in the low-field linear-response regime at a low temperature.

3 Scaling Analysis

Mathematically, the second-order phase transition around the Curie point T C could be described by the critical parameters β, δ and γ corresponding to spontaneous magnetization M spont(T,0), initial magnetic susceptibility χ 0(T), and the critical isotherm M(T C ,H), respectively. They are obtained through asymptotic relations [14]:

(1)
(2)
(3)

where M 0, h 0, and D are the critical amplitudes, and \(\varepsilon= \frac{T - T_{C}}{T_{C}}\) is the reduced temperature.

According to the critical region theory, the magnetic isotherms can be described by the magnetic equation of state

$$M(H,\varepsilon) =|\varepsilon|^{\beta} f_{\pm}\bigl(H/|\varepsilon|^{\beta+\gamma} \bigr) $$
(4)

where f + for T>T C and f − for T<T C , respectively, are regular functions. Equation (4) implies that M/|ε|β as a function H/|ε|β+γ, falls on two universal curves, one for temperatures above T C and the other for temperatures below T C .

4 Results and Discussion

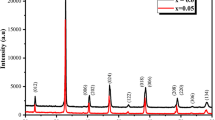
X-ray diffraction (XRD) patterns of all samples were recorded at room temperature and are shown in Fig. 1. The diffraction results indicate that all the samples are in single phase without any impurity and the samples have a rhombohedral lattice structure with space group \(R\overline{3}c\) (Z=6) in which La/Nd/Pb atoms are at 6a(0,0,1/4) positions, Mn/Ti at 6b(0,0,1/2), and O at 18e(x,0,1/4) position. The structure refinement was carried out by the Rietveld analysis of the X-ray powder diffraction data with the FULLPROF software [15]. On the basis of refined crystallographic data, the unit cell and atomic parameters and other fitting parameters of all samples were computed and are given in Table 1. Of fit parameters given by this program contains the weighted pattern R wp, the pattern R p , and the goodness of fit χ 2.

Fig. 1
figure 1

Rietveld plot of XRD data for polycrystalline La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0.05) pellet at 300 K. The points are the observed profile; the solid line is the calculated. Tick marks below the profile indicate the position of allowed Bragg reflections

Full size image
Table 1 Crystallographic data for La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0 and x=0.05) from the Rietveld refinement of X-ray diffraction data
Full size table

The magnetization versus temperature M(T) under an applied field of 500 Oe for the series La0.57Nd0.1Pb00.33Mn1−x Ti x O3 (x=0 and x=0.05) is shown in Fig. 2. Based on these results, paramagnetic-ferromagnetic (PM–FM) transition temperatures (T C ), were determined from the inflexion point of dM/dT versus T (K), as shown in the inset of Fig. 2. Obviously, substitution of Ti on the Mn site causes a reduction in the Curie temperature with increasing the Ti-doping level. We suggest that the T C reduction could be attributed to the distortion of MnO6 octahedron due to the gradual decreasing of the (Mn/Ti)–O–(Mn/Ti) bond angles and increasing of (Mn/Ti)–O; see Table 1. It causes decreasing in the mobility of e g electrons of Mn3+ that become more localized. Therefore, the double exchange interaction is weakened with increasing Ti doping in the samples. The reduction of T C should be related to the dilution of the Mn sublattice, i.e., the reduction of Mn4+ content results into dominance of ferromagnetic super exchange interaction between Mn cations [16, 17].

Fig. 2
figure 2

Temperature dependence of magnetization for La0.57Nd0.1Pb0.33Mn1−x Ti x O3 samples measured at 500 Oe

Full size image

Figure 3 shows the temperature dependence of the inverse magnetic susceptibility χ m deduced from M(T) at 500 Oe for all samples. Such behavior points out that the Griffiths-phase is completely absent in the corresponding data. For a ferromagnet, is well known that in the paramagnetic region, the relation between χ m and the temperature T should follow the Curie–Weiss law:

$$ \chi_{m} = \frac{C}{T - \theta_{P}}$$
(5)

where C is the Curie constant, and θ P is the Weiss temperature. The solid lines in Fig. 3 are the calculated curves deduced from the above Curie–Weiss equation.

Fig. 3
figure 3

Temperature-dependent of the inverse susceptibility, H/M for La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0 and x=0.05). The solid lines are the calculated curves according to Curie–Weiss law

Full size image

The paramagnetic Curie temperature θ P is obtained to the 351.15, and 319.35 K for the samples with x=0 and x=0.05, respectively. The positive value of θ P indicates the ferromagnetic interaction between spins. The experimental effective paramagnetic moments were calculated from \(C = \frac {N_{A}\mu _{B}^{2}}{3k_{B}}\mu_{\mathrm{eff}}^{2} \); with standard notations N A =6.023×1023 mol−1 is the number of Avogadro, μ B =9.274×10−21 emu is the Bohr magneton, and k B =1.38016×10−16 erg K−1 is the Boltzmann constant. The temperature range of fit, \(\theta_{P} \mu_{\mathrm{eff}}^{\mathrm{th}}\), and \(\mu_{\mathrm{eff}}^{\exp}\) are listed in Table 2. Furthermore, the reduction of the paramagnetic Curie temperature θ p with increasing of the Ti-doping level at B-site confirming the weakening of the ferromagnetic double exchange interaction and an increasing contribution of antiferromagnetic super exchange interactions.

Table 2 Transition temperature T C , θ p , \(\mu_{\mathrm{eff}}^{\mathrm{th}}\), and \(\mu_{\mathrm{eff}}^{\exp}\) as a function of x content for La0.57Nd0.1Pb0.33Mn1−x Ti x O3
Full size table

The exact determination of the temperature Curie T C and critical exponents β, δ and γ for LNPMT (x=0 and x=0.05) can be based on magnetization versus the applied field M(H) measured at various temperatures, known as magnetic isotherms. Here β, δ and γ are associated with the spontaneous magnetization M s (H=0), initial magnetic susceptibility χ 0=∂M/∂H/ H=0, and critical isotherm M(T C ,H), respectively [18]. Figure 3 shows the isotherms M versus H measurements were performed around the FM–PM phase transition temperature (T C ) for the series La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0 and x=0.05). The insets show plots of H/M vs. M 2. To determine the type of magnetic phase transition in La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0 and x=0.05) samples, we have analyzed H/M vs. M 2 curves (which were converted from the isothermal M–H data) using Banerjee criterion [19] and the results of which are presented in Fig. 4. According to this criterion, the magnetic transition is a first-order (second-order) if the slope of the plot H/M and M 2 is negative (positive). For all the samples, a second-order phase transition has been confirmed with the positive slope of H/M versus M 2 curve. According to the mean-field theory near T C , M 2 vs. H/M at various temperatures should show a series of parallel lines. The line at T=T C should pass through the origin. However, the curves in the Arrot plots are not linear for samples. This suggests that the mean-field theory is not valid for samples.

Fig. 4
figure 4

Magnetization vs. applied magnetic field H, measured at different temperatures, for La0.57Nd0.1Pb0.33Mn1−x Ti x O3 samples. Insets show Arrott plots H/M vs. M 2, for both compositions

Full size image

Thus, La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0 and x=0.05) has second-order phase transition and to characterize this we have taken recourse to which is commonly known as modified Arrott plot (MAP) [20]. This is given by the following equation of state:

$$( H/M )^{1/\gamma} = a( T - T_{C} )/T + bM^{1/\beta} $$
(6)

where a and b are considered to be constants.

Figures 5(a) and 5(b) show modified Arrott plots M 1/β vs. (H/M)1/γ constructed from the M vs. H plots at different temperatures by using trial critical exponents β and γ similar to those of three-dimensional (3D) Heisenberg magnets. This plot clearly shows the isotherms are a set of parallel straight in high magnetic fields. The line for T=T C passes through the origin on this plot. As trial values, we have chosen β=0.365 and γ=1.336, the critical exponents of the 3D-Heisenberg model. As this plot results in nearly straight lines, a linear extrapolation from fields above 2 kOe to the intercepts with the axes M 1/β and (H/M)1/γ gives the values of spontaneous magnetization M s (T) and inverse susceptibility \(\chi_{0}^{ - 1}(T)\), respectively. These values as functions of temperatures are plotted in Fig. 6. According to (1), slope of the straight line fitting of log[M s (T)] vs. log(ε) gives new value of β. Similarly, straight line fitting of \(\log[\chi_{0}^{ - 1}(T)]\) vs. log(ε) according to (2) gives new value of γ. Table 3 lists the results of the fits for the two compositions. Clearly, the values of critical parameters found for our samples completely agree with those of 3D-Heisenberg theory (see Table 3).

Fig. 5
figure 5

Modified Arrott plots of La0.57Nd0.1Pb0.33Mn1−x Ti x O3 for (a) x=0 and (b) 4x=0.05

Full size image
Fig. 6
figure 6

Spontaneous magnetization M s (left) and the inverse initial susceptibility \(\chi_{0}^{ - 1}\) (right) vs. temperature of La0.57Nd0.1Pb0.33Mn1−x Ti x O3 for (a) x=0 and (b) x=0.05

Full size image
Table 3 Values of the β, γ, and δ as determined from the modified Arrott plots, Kouvel–Fisher plot and the critical isotherm are given for La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0 and x=0.05). The theoretically predicted values of exponents for various universality classes are given for the sake of comparison
Full size table

Alternatively, the critical exponents can be obtained from the Kouvel–Fisher (KF) method as well [22].

(7)
(8)

According to this method, M s (dM s /dT)−1 vs. T and \(\chi_{0}^{ - 1}(d\chi_{0}^{ - 1}/dT)^{ - 1}\) vs. T yield straight lines with slopes 1/β and 1/γ, respectively. When these straight lines are extrapolated to the ordinate equal to zero, the intercepts on T axis just correspond to T C . These plots are shown in Fig. 7 for both compositions x. We have listed the critical exponents obtained from the modified Arrott plots as well as the Kouvel–Fisher method along with T C in Table 3.

Fig. 7
figure 7

Kouvel–Fisher plots of M s (T,0)[dM s (T,0)/dT]−1 and \(\chi_{0}^{ - 1}(T,0)[d\chi_{0}^{ - 1}(T,0)/\allowbreak dT]^{ - 1}\) vs. T for determination of β and γ in La0.57Nd0.1Pb0.33Mn1−x Ti x O3 for (a) x=0 and (b) x=0.05

Full size image

Concerning the value of δ, it can be determined directly from the critical isotherm M (T C ,H).

Figure 8 performs M(H) measured at some temperatures around T C on log–log scale. The fitting of the data near T C the slope 1/δ is determined. The values of δ obtained for two compositions are given in Table 3. The two exponents derived from our static scaling analysis are related by the Widom scaling relation [23]:

$$ \delta= 1 + (\gamma/\beta)$$
(9)

Using this scaling relation and the estimated values of β and γ, we obtain δ values which are close to the estimates for δ from the critical isotherms at T C , for both compositions studied. Thus, the estimates of the critical exponents are consistent. In the critical region, the magnetization and applied magnetic field should obey the universal scaling behavior.

Fig. 8
figure 8

M vs. H on a log–log scale around T=T C . The straight line is the linear fit following (3)

Full size image

In Figs. 9(a) and 9(b), we show plots of M|ε|−β vs. H|ε|−(β+γ) for x=0 and x=0.05, respectively. The two curves represent temperatures below and above T C . The inset shows the same data on a log–log plot. It can be clearly seen that all the points fall on two curves, one for T<T C another one for T>T C . This corroborates that the obtained values of the critical exponents and T C are reliable and in agreement with the scaling hypothesis.

Fig. 9
figure 9

Scaling plots for La0.57Nd0.1Pb0.33Mn1−x Ti x O3 for (a) x=0 and (b) x=0.05. The insets show the plots on a log–log scale

Full size image

The critical exponents obtained here is mostly close to the 3D-Heisenberg ferromagnet. As for the Heisenberg theory, the exchange integral is strongly dependent on the interaction distance. On the other hand, the universality class of the magnetic phase transition depends on the range of the exchange interaction J(r) in homogeneous magnets [24, 25]. The long-range attractive interactions decay as [25]

$$ J(r) \approx1/r^{ - (d + \sigma)}$$
(10)

where d is the spatial dimension, σ>0. For a three-dimensional material (d=3), there holds the relation J(r)≈1/r −(3+σ) with 3/2≤σ≤2. When σ=2, the Heisenberg exponents (β=0.365,γ=1.336, and δ=4.8) are valid for the three-dimensional isotropic ferromagnet, i.e., J(r) decreases faster than r −5. When σ=3/2, the mean-field exponents (β=0.5,γ=1 and δ=3) are valid, which indicates that J(r) decreases slower than r −4.5. All exponents obtained values of the 3D-Heisenberg model, which confirm that J(r) decays slower than r −5 for La0.57Nd0.1Pb0.33Mn1−x Ti x O3 (x=0 and x=0.05).

5 Conclusion

In summary, we have investigated the effect of Ti doping in La0.57Nd0.1Pb0.33MnO3 on the structural, magnetic, and critical parameters. The lattice parameters, unit cell volume, the (Mn/Ti)–O–(Mn/Ti) bond angle, and the (Mn/Ti)–O bond length increase with increasing Ti content. The Curie temperature T C is reduced by Ti doping level. The critical parameters β, γ, and δ estimated from various techniques match reasonably well. The values of the critical exponents are very close to the values for the 3D-Heisenberg ferromagnet with short-range interactions.