Two reliable wavelet methods to Fitzhugh–Nagumo (FN) and fractional FN equations

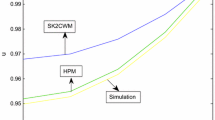
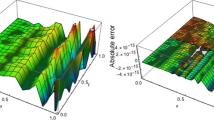
Abstract

Fractional reaction–diffusion equations serve as more relevant models for studying complex patterns in several fields of nonlinear sciences. In this paper, we have developed the wavelet methods to find the approximate solutions for the Fitzhugh–Nagumo (FN) and fractional FN equations. The proposed method techniques provide the solutions in rapid convergence series with computable terms. To the best of our knowledge, until now there is no rigorous wavelet solutions have been reported for the FN and fractional FN equations arising in gene propagation and model. With the help of Laplace operator and Legendre wavelets operational matrices, the FN equation is converted into an algebraic system. Finally, we have given some numerical examples to demonstrate the validity and applicability of the wavelet methods. The power of the manageable method is confirmed. Moreover, the use of the wavelet methods is found to be accurate, efficient, simple, low computation costs and computationally attractive.

Appendix

1.1 Basic idea of Homotopy analysis method (HAM)

In this section the basic ideas of the HAM are presented. Here a description of the method is given to handle the general nonlinear problem.

$$\begin{aligned} Nu_0 \left( t \right) =0, \;t>0 \end{aligned}$$

(7.1)

where N is a nonlinear operator and $u_0 (t)$ is unknown function of the independent variable t.

1.2 Zero-order deformation equation

Let $u_0 (t)$ denote the initial guess of the exact solution of Eq. (7.1), $\hbox {h}\ne 0$ an auxiliary parameter, $H(t)\ne 0$ an auxiliary function and L is an auxiliary linear operator with the property.

$$\begin{aligned} L\left( {f\left( t \right) } \right) =0, \quad f\left( t \right) =0. \end{aligned}$$

(7.2)

The auxiliary parameter h, the auxiliary function $H(t)$, and the auxiliary linear operator $L$ play an important role within the HAM to adjust and control the convergence region of solution series. Liao [26] constructs, using $q\in \left[ {0,1} \right]$ as an embedding parameter, the so-called zero-order deformation equation.

$$\begin{aligned} \left( {1-q} \right) L[(\emptyset \left( {t;q} \right) -u_0 \left( t \right) ]=qhH\left( t \right) N[\left( {\emptyset \left( {t;q} \right) } \right] , \end{aligned}$$

(7.3)

where $\emptyset \left( {t;q} \right)$ is the solution which depends on $\hbox {h},H\left( t \right) ,L, u_0 (t)$ and q. When q = 0, the zero-order deformation Eq. (7.2) becomes

$$\begin{aligned} \emptyset \left( {t;0} \right) =u_0 (t), \end{aligned}$$

(7.4)

and when q = 1, since ${\hbox {h}}\ne 0$ and $H(t)\ne 0$, the zero-order deformation Eq. (7.1) reduces to,

$$\begin{aligned} N\left[ {\emptyset \left( {t;1} \right) } \right] =0, \end{aligned}$$

(7.5)

So, $\emptyset \left( {t;1} \right)$ is exactly the solution of the nonlinear equation. Define the so-called $m$th order deformation derivatives.

$$\begin{aligned} u_m \left( t \right) =\frac{1}{m!}\frac{\partial ^{m}\emptyset \left( {t;q} \right) }{\partial q^{m}} \end{aligned}$$

(7.6)

If the power series Eq. (7.3) of $\emptyset \left( {t;q} \right)$ converges at q = 1, then we gets the following series solution:

$$\begin{aligned} u\left( t \right) =u_0 \left( t \right) +\sum \limits _{m=1}^\infty u_m \left( t \right) . \end{aligned}$$

(7.7)

where the terms $u_m \left( t \right)$ can be determined by the so-called high order deformation described below.

1.3 High-order deformation equation

Define the vector,

$$\begin{aligned} \overrightarrow{{u_{n}}=}\{u_0 \left( t \right) ,u_1 \left( t \right) ,u_2 \left( t \right) \ldots u_n \left( t \right) \end{aligned}$$

(7.8)

Differentiating Eq. (7.3) m times with respect to embedding parameter q, the setting q = 0 and dividing them by $m!$ , we have the so-called $m$th order deformation equation.

$$\begin{aligned} L\left[ {u_m \left( t \right) -\aleph _m u_{m-1} \left( t \right) } \right] =hH\left( t \right) R_m \left( {\overrightarrow{{u_m }},t} \right) , \end{aligned}$$

(7.9)

where

$$\begin{aligned} \aleph _m = \left\{ {{\begin{array}{l} { o,\quad m\le 1} \\ { 1,\quad otherwise} \\ \end{array} }} \right. \end{aligned}$$

(7.10)

and

$$\begin{aligned} R_m \left( {\overrightarrow{{u_m }},t} \right) =\frac{1}{\left( {m-1} \right) !}\frac{\partial ^{m-1}N[\emptyset (t;q)]}{\partial q^{m-1}} \end{aligned}$$

(7.11)

For any given nonlinear operator$N$, the term $R_m \left( {\overrightarrow{{u_m }},t} \right)$ can be easily expressed by Eq. (7.11). Thus, we can gain $u_1 \left( t \right) ,u_2 \left( t \right) \ldots \ldots$. by means of solving the linear high-order deformation with one after the other order in order. The $m^{th}$ –order approximation of u (t) is given by

$$\begin{aligned} u\left( t \right) =\sum _{k=0}^m {u_k \left( t \right) } \end{aligned}$$

(7.12)

ADM, VIM and HPM are special cases of HAM when we set $h=-1$ and $H\left( {r,t} \right) =1$. We will get the same solutions for all the problems by above methods when we set ${\hbox {h}}=-1$ and $H\left( {r,t} \right) =1$. When the base functions are introduced the $H\left( {r,t} \right) =1$ is properly chosen using the rule of solution expression, rule of coefficient of ergodicity and rule of solution existence.