1 Introduction

Individual happiness can be gauged using various methods, for example self-reports of life satisfaction, measures of positive and negative affect or indirect measures, such as the number of antidepressants consumed. A substantial amount of work has been devoted to study how happiness measured in such ways develops over the course of the lifetime. This allows insight into how happiness evolves alongside important life events, such as changes in employment status, getting married, having children, but also ageing in general. Studies in economics often find that happiness decreases from the teenage years to middle age, only to increase afterwards (and then to fall again in very high age). This dip in middle age is referred to as the U-shape of happiness and has been reported for a variety of countries (Bell & Blanchflower, 2020; Blanchflower, 2021; Blanchflower & Graham, 2021; Blanchflower & Oswald, 2008; Blanchflower & Piper, 2021; Gerdtham & Johannesson, 2001; Gwozdz & Sousa-Poza, 2010; Stone et al., 2010). This would indicate that people experience a low point of happiness around the age of 45–50. This dip is usually found to be comparable in magnitude to events such as getting divorced or losing employment (Blanchflower, 2021; Blanchflower & Graham, 2020). Taken together, this literature gives a persuasive reason to focus on this happiness dip as a researcher or policy maker. This is reflected in the attention this literature has received outside of academic research, reflected for example in articles in the Economist (2010) or the leading German weekly newspaper Die Zeit (Novotny, 2021), and many others.

At the same time, the U-shape around middle age has been contested by numerous other studies. Critique includes using the wrong controls (Glenn, 2009; Morgan & O’Connor, 2020), the wrong statistical model (Frijters & Beatton, 2012; Kratz & Brüderl, 2021; Ulloa et al., 2013), looking only at selected countries (Deaton, 2008), neglecting sample attrition in panels caused by higher mortality among the unhappiest respondents (Hudomiet et al., 2021), and not accounting for cohort effects (Ulloa et al., 2013). This critique in turn has produced several replies, indicating that the U-shape exists, even when accounting for these critiques (Blanchflower & Graham, 2020; Blanchflower & Oswald, 2009; Clark, 2019). A further criticism is that a lot of evidence on the U-shape stems from cross-sectional data (Galambos et al., 2020; Ulloa et al., 2013), although some studies confirm the U-shape based on longitudinal data (Cheng et al., 2017; Clark & Oswald, 2006; Van Landeghem, 2012). Looking at cross-sections might produce a U-shape because events can affect disparate age groups differently. Crucially, there seems to be no clear consensus in the literature on which statistical tools should be used to estimate the relationship between age and happiness.

In this paper, we aim to add to this debate by providing an account based on a large European database. We use SHARE (Survey of Health, Age and Retirement in Europe) data, which includes people 50 and upwards. Accordingly, we study if happiness increases after middle age, the right branch of the U-shape. SHARE is a multi-wave panel; hence we add to the literature by providing further evidence for longitudinal data. We use different specifications and control sets based on previous literature to provide a detailed account of the age-happiness relation in old age for 20 European countries. Our results indicate support for a U-shape around middle age in the sense that happiness increases with age after midlife. Congruent with other studies we also find that happiness starts to deteriorate at high age (Blanchflower, 2021; Blanchflower & Graham, 2020; Gwozdz & Sousa-Poza, 2010). These results are generally robust to the specification used, as well as to using different subsets of the sample to account for country, gender, or selection effects due to mortality. Some countries do not or not clearly exhibit a positive relation between age and happiness. However, these results might in part be driven by lack of sufficient observations for the individual countries.

2 Methodology

2.1 Data

We use waves 1 to 7 of the SHARE Release 7.0.0 (Survey of Health, Age and Retirement in Europe) database (Börsch-Supan et al., 2013; Börsch-Supan, 2018a, 2018b, 2018c, 2018d, 2018e, 2018f), except for wave 3. Wave 3 of SHARE (SHARELIFE) focused solely on past life events and does not include our target variables. SHARE is a database intended to be used to study the effects of ageing over the life-course of European citizens aged 50 and older, managed by the Munich Center for the Economics of Aging, Max Planck Institute for Social Law and Social Policy. The cross-national panel database provides extensive data on health and socio-economic status. We merge data over the above-mentioned six waves in order to track respondents over the course of the different interviews. Respondents over the age of 80 were dropped due to small sample size. In total, the merged data set has 139,116 individual observations. Theses waves interviewed the respondents from 2004 to 2017, spanning 13 years and 20 countries. During this time some participants left the study (due to death or other reasons), while others joined (especially because later waves include additional countries).

2.2 Measuring Happiness

Measuring happiness, well-being or life satisfaction is crucial to our research question. How happy, well or satisfied people are with their life can depend on multiple domains, such as employment, relationships, physical and mental health, financial situation or the fulfillment of goals and desires (Easterlin, 1974; Frey & Stutzer, 2002). Accordingly, one can elicit broad measures of happiness (the simplest would be to ask respondents directly “How happy are you with your life?”) or measures that zoom into specific domains. While there have been attempts to provide a unified, targetable index of happiness (such as Bhutan’s Gross National Happiness or the Happy Planet Index), there is no consensus how to best measure happiness. In our study, we utilize three measures to map respondents’ well-being: a simple single-item question regarding life satisfaction, the CASP-12 multi-item quality of life scale; and the EURO-D depressive symptoms scale. In the following, we discuss the three measures in more detail.

Our first measure, life satisfaction, measures a general, subjective feeling about the quality of life. It is extracted by a single-item question in which respondents indicate on a scale from 0 (low satisfaction) to 10 (high satisfaction) how satisfied they are with their life. This scale has acceptable reliability and validity (Beckie & Hayduk, 1997; Pavot & Diener, 1993) and relates meaningfully to various health and psychosocial measures (Kim et al., 2021).

Second, the CASP-12, a quality of life scale, which is designed to capture quality of life in old age (Hyde et al., 2003). Participants indicate for twelve statements whether they apply on a scale from 1 (often) to 4 (never). The twelve questions concern four dimensions of quality of life, control, autonomy, pleasure, and self-realization, resulting in an aggregate index ranging from 12 (low quality of life) to 48 (high quality of life). Hence, the CASP-12 relates more closely to affective measures or to the concept of eudemonia, where happiness follows from activity and control over one’s life (see Aristoteles’ Nicomachean Ethics, e.g. in Ameriks & Clarke, 2000). We normalize it such that it ranges from 0 (low quality of life) to 10 (high quality of life).

Our third measure is the EURO-D depression score (Prince et al. 1999b), which was designed to capture depressive symptoms among older people. It has been demonstrated to provide a valid comparison of depressive symptoms across European countries (Castro-Costa et al., 2008; Prince et al., 1999a). The EURO-D depression score is generated from questions on 12 dimensions: Depression, pessimism, suicidality, guilt, sleep, interest, irritability, appetite, fatigue, concentration, enjoyment, and tearfulness. The answers to these questions result in an aggregate index ranging from 0 (not depressed) to 12 (very depressed). We normalize it such that it ranges from 0 (very depressed) to 10 (not depressed) and call it lack of depressive symptoms, such that higher values of this index are comparable to higher values in the other two measures.

Table 8 in the appendix provides an overview of the specific questions asked for these three measures. In the following sections, we address these three measures collectively as measures of happiness, unless specified otherwise.

2.3 Controls

Different events and choices in a person’s life can influence the experienced level of happiness and life satisfaction (such as marrying, finding a better job, becoming a parent). If one wants to isolate the pure effect of ageing on happiness, one might want to control for such factors. On the other hand, these events are an inherent part of ageing. For example, many people become parents neither early nor very late in life. Controlling for such life events might thus lead to underestimating how happiness changes over the life course. If most of the important life events of a respondent are controlled for in their own variables, the effect of age is bound to become insignificant. As of yet, there appears to be no general agreement which set of controls should be included when analyzing happiness and life satisfaction in the literature.

Easterlin and Schaeffer (1999), Hellevik (2017) and Clark (2019) stressed the importance of controlling for cohort effects. Laaksonen (2018) showed that different controls sets can influence whether one obtains a U-shape (or any other specific form) in the first place. On the other hand, Frijters and Beatton (2012) favor fixed effects models that would exclude time-invariant controls, such as the birth cohort, in order to account for unobserved heterogeneity. Finally, a number of studies (Blanchflower, 2021; Blanchflower & Oswald, 2009) have shown that the U-shape can be obtained even without using any controls at all. More importantly, if and which controls are used should depend on the underlying research question: Specifications with controls can capture the pure effect of ageing, while abstracting from life events. Specifications without controls allow to estimate the overall trajectory of happiness over the life course (Blanchflower & Graham, 2020). A middle ground between those two approaches is to just include exogenous controls, that is only factors that remain constant over time, such as birth cohort or country of origin.

In order to accommodate the above outlined approaches, we conduct our analyses in the following ways: First, without any controls. Second, using a set of completely exogenous controls including gender, birth cohort, country of origin, and whether a respondent participated in all waves of the panel. Third, using a set of controls including the exogenous controls, as well as income, health and marriage/registered partnerships. Fourth, we use a fixed effect specification. One further concern can be the presence of selection effects: If less happy respondents are more likely to die early, they might disproportionally drop out of the panel, leading to a spurious positive correlation between age and happiness. Previous studies have indicated that different measures of happiness correlate positively with life expectation (Guven & Saloumidis, 2014; Kim et al., 2021; Lee & Singh, 2020). That is, older people could be happier, simply because their unhappier contemporaries are likely to die earlier and thus drop out of the pool of respondents. We control for this in three ways: First, we test whether we find evidence for such selection effects. Second, as we find such effects to be present (see Sect. 3.2.2), we control for respondents that participated in all waves as mentioned above. This gives us a primary indication if selection effects might be present. Third, we conduct our main analysis for both, the full sample of all respondents and a subsample of respondents participating in all waves, thus excluding selection effects.

For the analyses including controls, we use the following variables from the SHARE data set as controls: Relationship status (1 if the respondent is married or in a registered partnership, 0 otherwise), gender (1 if female, 0 if male), age (of the respondent at the time of the interview), age squared, self-assessed physical health (measured on a 5-point scale from “poor” to “excellent”), and a dummy variable indicating the country of residence of the respondent to control for cultural differences. Further, we include the level of education according to the international classification of education ISCED-97 and brackets for the average monthly household income, which represent country-specific 25th, 50th, and 75th percentiles of the reported household incomes from previous waves. This allows us to compare the effects of higher incomes across countries more easily. Additionally, we include a dummy variable for the birth cohort (which always covers a decade: 1930–1939, 1940–1949, etc.) and, as mentioned, a dummy variable for respondents that were present in all waves (subsequently called in all waves), to account for selection effects.

2.4 Models and Hypotheses

According to the previous sections, we estimate the following three models to test our research question. The observations of one participant in the different waves form a panel, standard errors are clustered on the level of the individual respondent.

$$M_{i,t} = \beta_{0} + \beta_{1} D^{\prime} + \gamma X^{\prime}_{i,t} + u_{i,t}$$
(1)
$$M_{i,t} = \beta_{0} + \beta_{1} Age_{i,t} + \beta_{2} Age_{i,t}^{2} + \gamma X_{i,t}^{\prime } + u_{i,t}$$
(2)
$$M_{i,t} = \beta_{1} Age_{i,t} + \beta_{2} Age_{i,t}^{2} + \gamma X_{i,t}^{\prime } + \alpha_{i} + u_{i,t}$$
(3)

Equation (1) is a pooled OLS regression using dummies for different age categories, (2) is a pooled OLS regression including terms for age and ages squared. These two models are intended as a very basic test of a possible age-happiness relation, similar to Blanchflower and Oswald (2009). Equation (3) specifies a fixed effects GLS model, which allows to eliminate unobserved heterogeneity between respondents (Frijters & Beatton, 2012).Footnote 1\({M}_{i,t}\) refers to our three happiness measures, life satisfaction, the CASP-12 index, and the EURO-D lack of depressive symptoms index, respectively (for individual \(i=1,\dots ,N\) and wave \(t=1, 2, 4, 5, 6, 7\)). \(D\) is a vector of dummies quantifying age tuples starting from 52 (based on the literature of Blanchflower & Oswald, 2009, pp. 52–53, 54–55, and so on), respondents of younger age than that form the reference category (a total of 9308 observations fall in this category). \(Ag{e}_{i,t}\) and \(Age_{i,t}^{2}\) refer to the age and the squared age of respondent i at time t. \({X}_{i,t}\) is a vector of time-varying (income brackets, education and subjective health) and time-invariant (gender, birth cohort and country of origin)Footnote 2 personal controls (see Sect. 2.3), \({\alpha }_{i}\) is the time-invariant personal effect of respondent i, and \({u}_{i,t}\) is an individual error term. As discussed in Sect. 2.3, models are run without controls, with only the exogenous controls, or with all controls, the latter two control sets being represented by \({X}_{i,t}\).

All three model specifications test the same underlying research question: Does happiness increase after middle age (in line with the right side of the U-shape), after which it stagnates and eventually drops at high age? As our sample includes only respondents of age 50 and upwards, these two factors would imply a hill shaped path for the three happiness measures after middle age. Or put differently, a positive coefficient for age and a negative one for age squared (as happiness tends to fall for high age). In other words, we test:

Hypothesis 1

The coefficients of the dummy variables \(\beta_{1}\) in model (1) are positive for lower ages, then close to zero and finally negative.

Hypothesis 2

The age coefficients \({\beta }_{1}\) are positive and the age-squared coefficients \({\beta }_{2}\) are negative in models (2) and (3) (implying a concave shape, which would indicate that happiness increases after middle age and drops towards the end of life).

Furthermore, we try to strengthen these hypotheses by running a series of robustness checks. First, as mentioned in Sect. 2.3, one important concern studying happiness and old age is the presence of selection effects. In order to see if this concern is well-founded in our data set, we run the following fixed effects logit models:

$$\Pr \left( {Y_{i,t} = 1|x_{i,t} } \right) = F\left( {\beta_{0} + \beta_{1} M_{i,t} + \gamma X_{i,t}^{\prime } + \alpha_{i} + u_{i,t} } \right)$$
(4)

where \(\mathrm{Pr}\left({Y}_{i,t}=1|{x}_{i,t}\right)\) is the probability that respondent i dies between wave t and wave t + 1 (Y = 1), \({M}_{i,t}\) refers again to our three happiness measures, \({X}_{i,t}\) refers to the vector of control variables, \({\alpha }_{i}\) is the time-invariant personal effect of respondent i, and \({u}_{i,t}\) is an individual error term. If more happy people (according to our measures) are indeed less likely to die, we expect \(\beta_{1}\) to be negative. As discussed in Sect. 2.3, we then take this into account for subsequent analyses. Additionally, our set of controls also contains the in all waves dummy variable. This allows us to capture any level effects caused by selection.

Second, we check whether our results differ if we perform some additional robustness checks. We run the regressions interacting the aforementioned in all waves dummy with the age and age squared variables. This provides further insight into the role of selection effects for the shape of the age-happiness relation. We also check if the age-happiness relation differs between male and female respondents, as well as between countries. Research has shown that the happiness of women and men differs (Laaksonen, 2018), and that the U-shape might be specific to some countries (Deaton, 2008). However, these control variables can only capture a level difference, not an overall different happiness-age pattern. Hence, we run our analyses again for men and women, as well as the different countries, separately.

3 Results

3.1 Summary Statistics

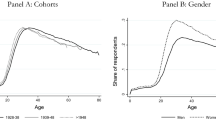
Table 1 provides an overview of key variables in our data set: the number of respondents per wave, percentages of female and married respondents, the average age, and our three variables on happiness and life satisfaction.Footnote 3 The number of respondents increases over the waves, as further countries and more respondents were added. At the same time, other respondents dropped out of the survey due to attrition, noticeable in the drop in wave 7. Figure 1 provides an overview of the number of respondents per country. As visible, the number of respondents can vary considerably relative to the population size of the country. We account for this fact in our inferential analyses by using the sampling weights provided by SHARE.Footnote 4 Figure 2 shows the share of the various birth cohorts over the different waves, indicating that e.g. most respondents in the 1930–1939 birth cohort dropped out of the survey at one point. Figure 3 shows the number of living respondents relative to those that died before the wave was conducted, giving an overview of how the sample evolved over time. Respondents that do not drop out of the survey are interviewed again in subsequent waves, which overall leads to the average age of respondents increasing slightly over the waves.

Table 1 Summary statistics of key variables
Full size table
Fig. 1
figure 1

Number of respondents per country

Full size image
Fig. 2
figure 2

Distribution of birth cohorts in the different waves

Full size image
Fig. 3
figure 3

Number of living and deceased respondents in the different waves

Full size image

Table 1 shows how the different measures for happiness and life satisfaction remained mostly stable on average over the waves. Before estimating the relationship between age and happiness, we can look at the raw answers to the different questions by age. Figure 4 shows the mean reported happiness over age pooled across all waves (see Figs. S1–S6 in the online supplement for graphs for the individual waves). As the figure indicates, happiness seems indeed to increase with age starting from a low point in middle age in the raw data, before dropping strongly at high age.

Fig. 4
figure 4

Raw values of the three happiness measures across all waves

Full size image

3.2 Main Analysis

3.2.1 Age and Happiness

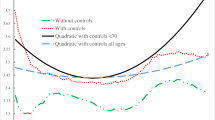
Next, we estimate the relationship between the happiness measures and age. First, we are considering model (1), the pooled OLS model using age dummies. Figure 5 depicts the coefficients of the age dummies plotted against age for all respondents, with the left panel showing results without sampling weights and the right panel with weights. The implied happiness increases for all three measures starting with middle age, but tend to flatten or decrease in old age (the latter is a common finding in other studies, see e.g. Blanchflower & Oswald, 2008 or Deaton, 2008). Including controls makes the increase after middle age even more pronounced, with the strong dip at old age becoming much less noticeable. A majority of the coefficients for the age dummies is highly significant (at p < 0.001, see Tables S1–S6 in the online supplement for the full regressions) and follow the predicted path: Earlier age dummies are positive, while later ones are either negative or positive but smaller and ultimately not significant. An exception to this seems to be life satisfaction, once the full control set is included. As factors such as deteriorating health and changes in marriage status are accounted for, life satisfaction appears to increase over the course of life.

Fig. 5
figure 5

Coefficients and confidence intervals of the age dummies model (1)

Full size image

Importantly, the effect sizes of the dummies (ranging from close to 0 to close to 1 at maximum) are similar to the results of other studies (Blanchflower, 2021; Blanchflower & Graham, 2020; Gwozdz & Sousa-Poza, 2010). To better illustrate the effect of ageing, we can also compare the effect sizes to that of important life events, such as getting divorced, losing a job, or losing a loved one (Blanchflower, 2021; Blanchflower & Graham, 2020). In our study for example, the effect of being married or in a registered partnership contributes between 0.171 and 0.411 to the happiness measures when using the full control set. Overall, these findings indicate a positive correlation between happiness and age with a tendency to flatten or decrease at high age, providing partial evidence in support of hypothesis 1.

Result 1

The coefficients of the dummy variables \(\upbeta_{1}\) in model (1) are positive after middle age. Towards higher age they tend to become closer to zero or negative, depending on the model and control set used. Happiness increases with age but flattens of falls towards high age.

These results are corroborated by the results of both the pooled OLS (2) and the fixed effects model (3) using age and age squared variables instead of dummies. Both models indicate an increase of all three measures over age that slows down, the older the respondents are. Table 2 displays the age and age squared coefficients of the pooled OLS model, again with and without sampling weights (the full regression tables are provided in Tables S7–S12 in the online supplementFootnote 5), Table 3 the ones of the fixed effects model (see Tables S19–S21 in the online supplement for the full regressions).Footnote 6 As we test multiple hypotheses here on the same data set, a concern might be that the obtained significant results are suffering from multiple hypothesis testing. Tables 2 and 3 thus also display the t-statistics for the two models. As these statistics show, our results are highly significant. Furthermore, the results obtained from the fixed effects model are overall remarkably close to the ones from the pooled OLS. This would suggest, at least for our data, that using either model leads to valid results. In addition, Table 4 depicts the turning points implied by our models, i.e., the age where happiness starts to decrease. Generally, the more controls are included, the higher the turning points become. This is as expected, as controlling for changes e.g., in health or family status isolates negative shocks are more likely to occur in higher age. For CASP-12 and EURO-D this results in the turning point moving upwards, with this change never exceeding 10 years. For life satisfaction this effect is more pronounced. In fact, in the OLS models the turning point moves beyond the age range of our sample once all controls are included. Taken together, these results corroborate that the increase in happiness after middle age slows down and might ultimately turn into a decrease later in life. Overall, we thus find evidence for hypothesis 2.

Table 2 Coefficients of the pooled OLS model (2) (using cohort dummies)
Full size table
Table 3 Coefficients of the fixed effects model (3)
Full size table
Table 4 Age turning points of the OLS model (2) (using cohort dummies) and the FE model (3)
Full size table

Result 2

The age coefficients \({\upbeta }_{1}\) are positive and significant and the age-squared coefficients \({\upbeta }_{2}\) are negative and significant in models (2) and (3). We find a concave shape for the age-happiness relation. Our results for CASP-12 and EURO-D indicate that happiness increases after middle age and drops towards the end of life. For life satisfaction, the drop becomes less pronounced as more controls are included.

3.2.2 Selection Effects

One major concern in the interpretation of the age effects shown in the previous sections is the presence of selection effects due to respondents dying depending on their happiness. Running fixed-effects logit regressions of the likelihood to die before a given wave on the different happiness measures (model 4 in Sect. 2.4), we find indeed evidence of a selection effect. The regression coefficients for the three happiness measures are all negative and significant for the CASP-12 and EURO-D lack of depressive symptoms (p < 0.05, p < 0.01 for lack depressive symptoms, see Table 10 in the appendix). The likelihood of dying before a given wave decreases by 0.000126, 0.000189 and 0.000347 percentage points for each point on the scales of life satisfaction, CASP-12, and EURO-D lack of depressive symptoms, respectively. We additionally find that respondents with better physical health status are less likely to die. In the preceding section, the full control set also included the in all waves dummy for respondents that were present in all waves. The coefficients for this dummy are positive (Life satisfaction: 0.0412 [2.38], CASP: 0.104 [5.77], Lack of depressive symptoms: 0.0724 [3.68], t-statistics in square brackets, pooled OLS regression).

However, these coefficients can only account for a level effect between respondents that took part in all waves and those that dropped out of the sample at one point. To test if selection affects the shape of the happiness-age relation, we run our analyses for the subset of respondents that participated in all waves. Note that in the latter subset we also drop respondents that did not die between the waves, but either dropped out due to other reasons, or only joined the panel during the later waves. Past studies highlighted the fact that cross-sectional studies do not follow respondents over the life cycle and might thus have limited explanatory power (Galambos et al., 2020; Hudomiet et al., 2021; Ulloa et al., 2013): Accordingly, this subset represents the most stringent subset of respondents, specifically those for which we can track happiness over all waves.

Figure 6 shows the dummy coefficients of model (1) for the no attrition subset.Footnote 7 Looking at this subset, the obtained relationship between happiness and age emerges again, but loses part of its significance depending on the control set (in terms of the number of significant age dummies (see Tables S22–S27 in the online supplement for the full regression). However, these results might in part be driven by the sharp decrease in observations once controls are used in the already strict no attrition subsample.

Fig. 6
figure 6

Coefficients of the age dummies model (1), no attrition subsample

Full size image

Tables 5 and 6 depict the age and age squared coefficients of the pooled OLS and fixed effects models (see Tables S28–S36 in the online supplement for the full regressions). The estimated coefficients are all highly significant and fit our predictions. Comparing Tables 2 and 3, 4, 5 and 6 shows that the coefficients are comparable in sign and size across the full sample and the no attrition subsample. We take this as further indication that selection effects are in place, but do not account for the observed correlation between happiness and age. Taking the findings of this section together, there is clear evidence that, while selection effects play a role, they seem to matter in the form of a level effect, rather than influencing the shape of the age-happiness relation. Notably, these results differ from the recent study of Hudomiet et al. (2021), which reports a decline in subjective well-being in U.S. data, as soon as attrition due to mortality is accounted for. Overall, our results are comparable, irrespective of whether we use sampling weights, account for attrition, using fixed effects, or using no or only exogenous controls. For the following subsample analysis, we hence use pooled OLS, sampling weights and the full set of controls for simplicity.

Table 5 Coefficients of the pooled OLS model (2) (using cohort dummies), no attrition subsample
Full size table
Table 6 Coefficients of the fixed effects model (3), no attrition subsample
Full size table

As a further robustness check, we run the weighted pooled OLS again, this time interacting the aforementioned in all waves dummy with the age and age squared variables (see Table 11 in the appendix and Table S37 in the online supplement). These interactions effects, as well as the in all waves dummy itself are in most cases insignificant. However, the coefficients for age and age squared still exhibit the same pattern in our main analysis. A notable exception is the CASP-12: Including the interaction effects here renders the in all waves dummy itself significant, but negative. The interaction effects with age and age squared are significant, and are also positive and negative, respectively. In other words, even in this exception, respondents that took part in all waves exhibit the same age-happiness pattern as in the main analysis. If anything, the pattern emerges even stronger here.

3.3 Subsample Analyses

3.3.1 Gender Differences

Looking at men and women separately, the results of the dummy regressions in Fig. 7 already indicate that the age-happiness relation follows a comparable path for both genders (see Tables S38–S39 in the online supplement for the full regressions). Table 7 shows the coefficients and t-statistics for the pooled OLS model (1) (see Tables S40–S41 in the online supplement for the full regressions). In general, the results look similar for both men and women. However, for women, the pattern is less pronounced, falling just short of reaching significance for some of the coefficients in the pooled OLS model, except for the CASP-12. We run the same regression with interaction terms (see Table 12 in the appendix and Table S42 in the online supplement). None of the interaction terms are significant, corroborating that the fundamental pattern is similar for men and women.

Fig. 7
figure 7

Coefficients and confidence intervals of the age dummies model (1) for men and women, all respondents

Full size image
Table 7 Coefficients of the pooled OLS model (2), men and women
Full size table

3.3.2 Country Differences

Next, we turn to the differences between the countries of the SHARE data set. For the dummy regression plots for the 20 individual countries, see Fig. 8 in the appendix (full dummy regressions in Tables S43–S62 in the online supplement). For an overview of all age and age squared coefficients of the pooled OLS how to best measure happiness best model, see Table 13 in the appendix (full dummy regressions in Tables S63–S82 in the online supplement). Evidence from the pooled OLS model here is mixed, with some countries not observing a significant correlation between age and happiness at all (or only for some of the happiness measures used). Still, for all countries and measures for which a significant correlation is observed, the positive trend for happiness with age and the negative with age squared is obtained. Notably, however, the pooled OLS with age coefficients and pooled OLS dummy regressions do not always agree in terms of the significance level. Belgium (panel 2 in Fig. 8) for example exhibits a positive relation between age and happiness for life satisfaction and the CASP-12, while the corresponding coefficients in the pooled OLS regression fail to reach significance.

Of course, conducting the analysis for each country separately with the full control set additionally atomises the data. This is only exacerbated by different countries having differing sample sizes in the data set to begin with. As measures such as the question on life satisfaction appear in many questionnaires, our results could be complemented by studying larger national data sets. Alternatively, future waves of SHARE might include further data to answer the question if the observed insignificances are caused here by a lack of data points or by some countries not exhibiting a positive relation between age and happiness.

4 Discussion

Studies measuring happiness and well-being over the life cycle have found mixed results, and in particular the U-shape of happiness is a controversial finding. Consistent with a U-shape around middle age, we find that happiness increases after the age of 50, irrespective of the specification used. Furthermore, our results indicate that happiness tends to stagnate or even decrease at very high age. When conducting our analysis on country- or gender-specific subsamples, a more varied picture emerges. Where we find significant results in these subsamples, however, it is always consistent with a U-shape. These findings are also robust when accounting for differences due to mortality selection effects. While selection effects are indeed at work, with happier respondents being more likely to be alive at the time the next wave is elicited, CASP-12 is the only measure where the pattern is affected: selection makes the observed pattern more pronounced in this case. The result could potentially stem from the CASP-12 measuring control and agency, which decrease towards the end of one’s life (Oliver et al., 2021; Ribeiro et al., 2020; Rodríguez-Blázquez et al., 2020). This might also help to explain why we find lower turning points for CASP-12 and EURO-D in Table 4 in contrast to life satisfaction, when including additional controls. One reason why life satisfaction might continue to increase in high age is that older people might give up on aspiration and enjoy life more (Blanchflower & Oswald, 2004; Frey & Stutzer, 2010). CASP-12 and EURO-D, on the other hand, measure elements related to control and mental health, which might be more negatively affected by age. Different happiness measures might capture different aspects of life, highlighting the importance of looking at multiple measures at the same time.

Importantly, the observed age-happiness relation is consistently obtained using different approaches that have been used in both research that found and did not find the happiness dip in middle age. Additionally, the happiness-age relationship does not only hold for measures of subjective well-being (life satisfaction), but also for affective/eudemonic (CASP-12) and mental health measures (EURO-D). We are thus confident that our findings are meaningful for a substantial number of European countries.

Naturally, we can make no predictions about the trajectory of the happiness-age relation under the age of 50, as the SHARE data set only provides data for older Europeans. However, as other studies have indicated, there is support for the overall U-shape in various European countries (Blanchflower, 2021). We find that happiness indeed increases after middle age, compared to other studies finding a decrease after middle age (Easterlin, 2006; Mroczek & Spiro, 2005) or an overall decrease (Frijters & Beatton, 2012; Kassenboehmer & Haisken-DeNew, 2012). These differences could reflect regional differences, as Easterlin (2006) and Mroczek and Spiro (2005) use US data. Alternatively, methodological differences might drive these divergences. Kassenboehmer and Haisken-DeNew (2012) utilize respondents leaving the survey panel temporarily, to differentiate between age and years in the survey. Both should still be correlated, however. Frijters and Beatton’s (2012) main result is based on fixed effects regressions, which might ultimately not be reliable enough to deal with the age-period-cohort problem (Heckman & Robb Jr, 1985; Yang & Land, 2008). Mrozcek and Spiro’s (2005) use of a demeaned variable in their specification might similarly be problematic (McIntosh & Schlenker, 2006).

Our results are in line with previous studies indicating an increase of happiness after 50 (Morgan & O’Connor, 2017) or an upward profile for affective measures (Mroczek & Kolarz, 1998). However, similar to other studies, our results also provide evidence that happiness, depending on the measure used, stagnates or even decreases later in life (Blanchflower, 2021; Blanchflower & Graham, 2020; Gwozdz & Sousa-Poza, 2010). Our results support the view that people go through a period of relatively low happiness (relative to happiness at older age) around the midpoint of their life. For policy makers, it is important to further explore why this dip occurs and how it can be alleviated.

Going forward, it is important to highlight that proving or disproving the U-shape of happiness, or as in our case components of it, should not be a goal in itself. While knowing the average path happiness takes over the course of a human life is important, even more so is understanding which life events affect the emerging trajectory (Bjørnskov et al., 2008; Galambos et al., 2020, 2021; Lachman, 2015; Morgan & O’Connor, 2020). Past research has shown the happiness effects of marriage (Grover & Helliwell, 2019), parenthood (Nelson et al., 2013), social networks in general (Becker et al., 2019), income (Easterlin, 1974), social support (Siedlecki et al., 2014), permanent employment (Piper, 2021), the quality of formal institutions (Bjørnskov et al., 2010), giving up on aspirations (Schwandt, 2016), and health (Bussière et al., 2021; Gwozdz & Sousa-Poza, 2010; Oliver et al., 2021). Mapping the evolution of these events over the life course may help to better understand the emergence of the U-shape of happiness.