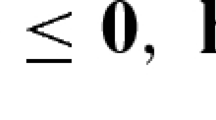Convergence-order analysis of branch-and-bound algorithms for constrained problems

Abstract

The performance of branch-and-bound algorithms for deterministic global optimization is strongly dependent on the ability to construct tight and rapidly convergent schemes of lower bounds. One metric of the efficiency of a branch-and-bound algorithm is the convergence order of its bounding scheme. This article develops a notion of convergence order for lower bounding schemes for constrained problems, and defines the convergence order of convex relaxation-based and Lagrangian dual-based lower bounding schemes. It is shown that full-space convex relaxation-based lower bounding schemes can achieve first-order convergence under mild assumptions. Furthermore, such schemes can achieve second-order convergence at KKT points, at Slater points, and at infeasible points when second-order pointwise convergent schemes of relaxations are used. Lagrangian dual-based full-space lower bounding schemes are shown to have at least as high a convergence order as convex relaxation-based full-space lower bounding schemes. Additionally, it is shown that Lagrangian dual-based full-space lower bounding schemes achieve first-order convergence even when the dual problem is not solved to optimality. The convergence order of some widely-applicable reduced-space lower bounding schemes is also analyzed, and it is shown that such schemes can achieve first-order convergence under suitable assumptions. Furthermore, such schemes can achieve second-order convergence at KKT points, at unconstrained points in the reduced-space, and at infeasible points under suitable assumptions when the problem exhibits a specific separable structure. The importance of constraint propagation techniques in boosting the convergence order of reduced-space lower bounding schemes (and helping mitigate clustering in the process) for problems which do not possess such a structure is demonstrated.

Proofs

1.1 Proof of Proposition 1

Proposition 1

Consider Problem (P) with $m_E = 0$. Suppose f and $g_j, \forall j \in \{1,\ldots ,m_I\}$, are Lipschitz continuous on $X \times Y$. Furthermore, suppose $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in X \times Y$ such that ${\mathbf {g}}({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) < {\mathbf {0}}$ (i.e. $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$ is a Slater point). The dual lower bounding scheme has arbitrarily high convergence order at $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$.

Proof

The arguments below are closely related to the proof of Corollary 2.

Since we wish to prove that the dual lower bounding scheme has arbitrarily high convergence order at the feasible point $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$, it suffices to show that for each $\beta > 0$, there exists $\tau \ge 0, \delta > 0$ such that for every $Z \in {\mathbb {I}}(X \times Y)$ with $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in Z$ and $w(Z) \le \delta$,

$$\begin{aligned} \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) - \underset{\varvec{\mu }\ge {\mathbf {0}}}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min }\left[ f({\mathbf {x}},{\mathbf {y}})+{\varvec{\mu }}^\text{ T }{\mathbf {g}}({\mathbf {x}},{\mathbf {y}})\right] \le \tau {w(Z)}^{\beta }, \end{aligned}$$

and the desired result follows by analogy to Lemma 5 by observing that the dual lower bounding scheme is at least first-order convergent at $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$.

Let $g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) = -\varepsilon _j < 0, \forall j \in \{1,\ldots ,m_I\}$. Since $g_j$ is continuous for each $j \in \{1,\ldots ,m_I\}$, there exists $\delta _j > 0, \forall j \in \{1,\ldots ,m_I\}$, such that ${||}({\mathbf {x}},{\mathbf {y}}) - ({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){||}_{\infty } < \delta _j$ implies ${|}g_j({\mathbf {x}},{\mathbf {y}}) - g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){|} < \frac{\varepsilon _j}{2}$ (see Lemma 2).

Define $\delta := {\mathop {\min }\limits _{j \in \{1,\ldots ,m_I\}}}{\delta _j}$, and note that $\delta > 0$. Consider $Z \in {\mathbb {I}}(X \times Y)$ such that $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}) \in Z$ and $w(Z) \le \delta$. For each $({\mathbf {x}},{\mathbf {y}}) \in Z, j \in \{1,\ldots ,m_I\}$ we have ${|}g_j({\mathbf {x}},{\mathbf {y}}) - g_j({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }}){|} < \frac{\varepsilon _j}{2}$. Therefore, for each $j \in \{1,\ldots ,m_I\}, g_j({\mathbf {x}},{\mathbf {y}})< -\frac{\varepsilon _j}{2} < 0, \,\forall ({\mathbf {x}},{\mathbf {y}}) \in Z$. Consequently,

$$\begin{aligned} \underset{\varvec{\mu }\ge {\mathbf {0}}}{\sup }\,\,\underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } {\left[ f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}})\right] }&\ge \underset{({\mathbf {x}},{\mathbf {y}}) \in Z}{\min } f({\mathbf {x}},{\mathbf {y}}) \\&= \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}{\min } f({\mathbf {x}},{\mathbf {y}}) \end{aligned}$$

since Problem (P) is effectively unconstrained over the small intervals Z around $({\mathbf {x}}^{\text{ S }},{\mathbf {y}}^{\text{ S }})$, which implies $\tau = 0$ and $\delta = \underset{j \in \{1,\ldots ,m_I\}}{\min }{\delta _j}$ satisfy the requirements. $\square$

1.2 Proof of Proposition 2

Proposition 2

Consider Problem (P) with $m_E = 0$. Suppose the functions f and $g_j, j = 1,\ldots ,m_I$, are each of the form (W). Let $(f^{\text{ cv }}_{X(Z) \times Z})_{Z \in {\mathbb {I}}Y}$ denote a continuous scheme of convex relaxations of f in Y with convergence order $\beta ^{\text{ cv }}_f > 0$ and corresponding constant $\tau ^{\text{ cv }}_f, (g^{\text{ cv }}_{j,X(Z) \times Z})_{Z \in {\mathbb {I}}Y}, j = 1,\ldots , m_I$, denote continuous schemes of convex relaxations of $g_1,\ldots ,g_{m_I}$, respectively, in Y with pointwise convergence orders $\gamma ^{\text{ cv }}_{g,1}> 0, \ldots , \gamma ^{\text{ cv }}_{g,m_I} > 0$ and corresponding constants $\tau ^{\text{ cv }}_{g,1}, \ldots , \tau ^{\text{ cv }}_{g,m_I}$.

Suppose ${\mathbf {y}}^{\text{ S }} \in Y$ is an unconstrained point in the reduced-space, and the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ with

$$\begin{aligned}&\displaystyle ({\mathscr {O}}(Z))_{Z \in {\mathbb {I}}Y} := \left( \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)}{\min }f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}})\right) _{Z \in {\mathbb {I}}Y}, \\&\displaystyle ({\mathscr {I}}_{C}(Z))_{Z \in {\mathbb {I}}Y} := \left( \overline{{\mathbf {g}}}^{\text{ cv }}_{X(Z) \times Z}(X(Z) \times Z)\right) _{Z \in {\mathbb {I}}Y} \end{aligned}$$

has convergence of order $\beta \in (0,\beta ^{\text{ cv }}_f]$ at ${\mathbf {y}}^{\text{ S }}$. Then the scheme of lower bounding problems $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ is at least $\beta ^{\text{ cv }}_f$-order convergent at ${\mathbf {y}}^{\text{ S }}$.

Proof

The proof is similar to the proof of Corollary 2.

Since ${\mathbf {y}}^{\text{ S }}$ is an unconstrained point in the reduced-space and $g_j$ is continuous for each $j \in \{1,\ldots ,m_I\}$ by virtue of Assumption 1, $\exists \delta > 0$ such that $\forall {\mathbf {z}}\in Y$ with ${||}{\mathbf {z}}- {\mathbf {y}}^{\text{ S }}{||}_{\infty } \le \delta$ (see Lemma 2), we have ${\mathbf {g}}({\mathbf {x}},{\mathbf {z}}) < {\mathbf {0}}, \forall {\mathbf {x}}\in X$.

Consider $Z \in {\mathbb {I}}Y$ with ${\mathbf {y}}^{\text{ S }} \in Z$ and $w(Z) \le \delta$. We have $\overline{{\mathbf {g}}}(X(Z) \times Z) \subset {\mathbb {R}}^{m_I}_{-}$ and $\overline{{\mathbf {g}}}^{\text {cv}}_{X(Z) \times Z}(X(Z) \times Z) \subset {\mathbb {R}}^{m_I}_{-}$. Consequently,

$$\begin{aligned}&\quad \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}^{\text{ cv }}(Z)} f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \\&= \min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z}f({\mathbf {x}},{\mathbf {y}}) \,\, - \min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z} f^{\text{ cv }}_{X(Z) \times Z}({\mathbf {x}},{\mathbf {y}}) \\&\le \tau ^{\text {cv}}_f w(Z)^{\beta ^{\text {cv}}_f}. \end{aligned}$$

The desired result follows by analogy to Lemma 5 based on the assumption that $({\mathscr {L}}(Z))_{Z \in {\mathbb {I}}Y}$ is at least $\beta$-order convergent at ${\mathbf {y}}^{\text{ S }}$. $\square$

1.3 Proof of Proposition 3

Proposition 3

Consider Problem (P) with $m_E = 0$. Suppose ${\mathbf {y}}^{\text{ S }} \in Y$ is an unconstrained point in the reduced-space. Furthermore, suppose the reduced-space dual lower bounding scheme has convergence of order $\beta > 0$ at ${\mathbf {y}}^{\text{ S }}$. Then the reduced-space dual lower bounding scheme has arbitrarily high convergence order at ${\mathbf {y}}^{\text{ S }}$.

Proof

The proof is closely related to the proof of Proposition 1.

Since ${\mathbf {y}}^{\text{ S }}$ is an unconstrained point in the reduced-space and $g_j$ is continuous for each $j \in \{1,\ldots ,m_I\}$ by virtue of Assumption 1, there exists $\delta > 0$ such that $\forall {\mathbf {z}}\in Y$ satisfying ${||}{\mathbf {z}}- {\mathbf {y}}^{\text{ S }}{||}_{\infty } \le \delta$ (see Lemma 2), we have ${\mathbf {g}}({\mathbf {x}},{\mathbf {z}}) < 0, \forall {\mathbf {x}}\in X$.

Consider $Z \in {\mathbb {I}}Y$ with $w(Z) \le \delta$. Since $\overline{{\mathbf {g}}}(X(Z) \times Z) \subset {\mathbb {R}}^{m_I}_{-}$, Problem (P) can be reformulated as

$$\begin{aligned} \underset{({\mathbf {x}},{\mathbf {y}}) \in {\mathscr {F}}(Z)}{\min } f({\mathbf {x}},{\mathbf {y}}) = \min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z} f({\mathbf {x}},{\mathbf {y}}). \end{aligned}$$

The dual lower bound can be bounded from below as

$$\begin{aligned} \sup _{\varvec{\mu }\ge {\mathbf {0}}}\min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z} \left[ f({\mathbf {x}},{\mathbf {y}}) + {\varvec{\mu }}^\text{ T } {\mathbf {g}}({\mathbf {x}},{\mathbf {y}})\right] \ge \min _{({\mathbf {x}},{\mathbf {y}}) \in X(Z) \times Z} f({\mathbf {x}},{\mathbf {y}}). \end{aligned}$$

The desired result follows by analogy to Lemma 5 and the assumption that the dual lower bounding scheme is at least $\beta$-order convergent at ${\mathbf {y}}^{\text{ S }}$. $\square$

1.4 Proof of arguments in Example 18

Proof

We first show that $x^{\text{ f }}_Z - x^* \ge 0.2\varepsilon + o\left( \varepsilon \right)$.

$$\begin{aligned}&x^{\text{ f }}_Z - x^*\\ {}&\quad = \, \Bigg ( \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40 + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) } - \exp (3 - y^{\text{ U }})}{2} \\&\quad \quad \quad - \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} - \exp (3 - y^*)}{2} \Bigg ) \\&\quad = \, \displaystyle \frac{ \left( \left( \exp (3 - y^{\text{ U }}) \right) ^2 - \left( \exp (3 - y^*) \right) ^2 \right) + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40 + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) } + \displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} \right) } \\&\quad \quad \quad + \displaystyle \frac{\left( \exp (3 - y^*) - \exp (3 - y^{\text{ U }}) \right) }{2} \\&\quad = \, \displaystyle \frac{ \left( \exp (3 - y^{\text{ U }}) + \exp (3 - y^*) + 2 \right) \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ U }}) \right) ^2 + 40 + 2 \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) } + \displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} \right) } \\&\quad \quad \quad + \displaystyle \frac{\left( \exp (3 - y^*) - \exp (3 - y^{\text{ U }}) \right) }{2} \\&\quad \ge \displaystyle \frac{ \left( \exp (3 - y^*) + \exp (3 - y^*) + 2 \right) \left( \exp (3 - y^{\text{ U }}) - \exp (3 - y^*) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^* - 0.1) \right) ^2 + 40 + 2 \left( \exp (3 - y^* - 0.1) - \exp (3 - y^*) \right) } + \displaystyle \sqrt{\left( \exp (3 - y^*) \right) ^2 + 40} \right) } \\&\quad \quad \quad + \displaystyle \frac{\left( \exp (3 - y^*) - \exp (3 - y^{\text{ U }}) \right) }{2} \\&\quad \ge \, 0.025 \left( \exp (3 - y^*) - \exp (3 - y^{\text{ U }}) \right) \\&\quad = \, 0.025 \exp (3 - y^*) \varepsilon + o\left( \varepsilon \right) \\&\quad \ge \, 0.2\varepsilon + o\left( \varepsilon \right) . \end{aligned}$$

Next, we derive an expression for ${\bar{x}}_Z(y) - x^*(y)$.

$$\begin{aligned} {\bar{x}}_Z(y) - x^*(y)&= \, \Bigg ( \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } - \exp (3 - y^{\text{ L }})}{2} \nonumber \\&\quad \quad \quad - \displaystyle \frac{\displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} - \exp (3 - y)}{2} \Bigg ) \nonumber \\&= \, \displaystyle \frac{ \left( \left( \exp (3 - y^{\text{ L }}) \right) ^2 - \left( \exp (3 - y) \right) ^2 \right) + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) } \nonumber \\&\quad \quad \quad + \displaystyle \frac{\left( \exp (3 - y) - \exp (3 - y^{\text{ L }}) \right) }{2} \nonumber \\&= \, \displaystyle \frac{ \left( \exp (3 - y^{\text{ L }}) + \exp (3 - y) + 4x^{\text{ U }}_Z \right) \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) } \nonumber \\&\quad \quad \quad - \displaystyle \frac{\left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2}. \end{aligned}$$

(11)

We next establish the dependence of the different terms in Eq. (11) on $\varepsilon$. We first derive an expression for $\exp (3 - y^{\text{ L }}) + \exp (3 - y) + 4x^{\text{ U }}_Z$.

$$\begin{aligned}&\qquad \! \exp (3 - y^{\text{ L }}) + \exp (3 - y) + 4x^{\text{ U }}_Z \\&= \, \exp (3-y^*+\varepsilon ) + \exp (3-y) + 2\displaystyle \sqrt{\left( \exp (3-y^*-\varepsilon \right) ^2 + 40} - 2\exp (3-y^*-\varepsilon ) \\&= \, \exp (3-y^*) + \exp (3-y) + \varepsilon \exp (3-y^*) + O(\varepsilon ^2) \\&\quad \quad + 2\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 \left[ 1 - 2\varepsilon + O(\varepsilon ^2) \right] + 40}-2\exp (3-y^*)\left[ 1 - \varepsilon + O(\varepsilon ^2) \right] \\&= \, 2\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} + \exp (3-y) - \exp (3-y^*) + 3\exp (3-y^*)\varepsilon \\&\quad \quad - \displaystyle \frac{2\left( \exp (3-y^*) \right) ^2 \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} + O(\varepsilon ^2). \end{aligned}$$

Next, we derive an expression for $4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right)$.

$$\begin{aligned}&4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) \\&\quad = \, \left( 2\displaystyle \sqrt{\left( \exp (3-y^*-\varepsilon \right) ^2 + 40} - 2\exp (3-y^*-\varepsilon ) \right) \left( \exp (3-y^*+\varepsilon ) - \exp (3-y) \right) \\&\quad = \, \left( 2\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - 2\exp (3-y^*) \right) \left( \exp (3-y^*+\varepsilon )- \exp (3-y) \right) + O(\varepsilon ^2) \\&\quad = \, \left( 2\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - 2\exp (3-y^*) \right) \left( \exp (3-y^*) - \exp (3-y) +\exp (3-y^*)\varepsilon \right) \\ {}&\quad \quad \quad + O(\varepsilon ^2). \end{aligned}$$

Finally, we consider $\sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40}$.

$$\begin{aligned}&\, \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} \\&\quad = \, \displaystyle \sqrt{\left( \exp (3-y^*+\varepsilon )\right) ^2 + 40 + 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) } + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} \\&\quad = \, \displaystyle \sqrt{\left( \exp (3-y^*)\right) ^2 + 40} \displaystyle \sqrt{1 + \displaystyle \frac{4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) + 2\left( \exp (3-y^*)\right) ^2 \varepsilon + O(\varepsilon ^2)}{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} \\&\quad = \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} + \displaystyle \frac{\left( \exp (3-y^*)\right) ^2 \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad {+} \displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 {+} 40} {-} \exp (3-y^*) \right) \left( \exp (3-y^*) {-} \exp (3-y) {+} \exp (3-y^*) \varepsilon \right) }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 {+} 40}} {+} O(\varepsilon ^2). \end{aligned}$$

Substituting the above expressions in Eq. (11), we get

$$\begin{aligned}&\qquad {\bar{x}}_Z(y) - x^*(y) \\&= \, \displaystyle \frac{ \alpha \left( \exp (3 - y^{\text{ L }}) - \exp (3 - y) \right) }{2\left( \displaystyle \sqrt{\left( \exp (3 - y^{\text{ L }}) \right) ^2 + 40 {+} 4x^{\text{ U }}_Z \left( \exp (3 - y^{\text{ L }}) {-} \exp (3 - y) \right) } {+} \displaystyle \sqrt{\left( \exp (3 - y) \right) ^2 + 40} \right) }, \end{aligned}$$

with

$$\begin{aligned} \alpha&:= \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40} + \exp (3-y) - \exp (3-y^*) \\&\quad \quad \quad - \displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \exp (3-y^*) \right) \left( \exp (3-y^*) - \exp (3-y) \right) }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad + 3\exp (3-y^*) \varepsilon - \displaystyle \frac{3\left( \exp (3-y^*) \right) ^2 \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad - \displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \exp (3-y^*) \right) \exp (3-y^*) \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} + O(\varepsilon ^2) \\&\quad = \left( \displaystyle \frac{\exp (3-y^*) + \exp (3-y)}{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} + \displaystyle \sqrt{\left( \exp (3-y) \right) ^2 + 40}} - 1 \right) \left( \exp (3-y^*) - \exp (3-y) \right) \\&\quad \quad \quad -\displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \exp (3-y^*) \right) \left( \exp (3-y^*) - \exp (3-y) \right) }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad + 3\exp (3-y^*) \varepsilon - \displaystyle \frac{3\left( \exp (3-y^*) \right) ^2 \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} \\&\quad \quad \quad - \displaystyle \frac{\left( \displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40} - \exp (3-y^*) \right) \exp (3-y^*) \varepsilon }{\displaystyle \sqrt{\left( \exp (3-y^*) \right) ^2 + 40}} + O(\varepsilon ^2) \\&\quad \le {\hat{\tau }} \varepsilon + O(\varepsilon ^2) \end{aligned}$$

for some ${\hat{\tau }} \ge 0$ since $y \in Z = [y^{\text{ L }}, y^{\text{ U }}]$ with $w(Z) = O(\varepsilon )$ and each term in the expression for $\alpha$ is $O(\varepsilon )$. Note that $\alpha \ge 0$ (since $\bar{x}_Z(y) \ge x^*(y), \, \forall y \in Z$). $\square$