Introduction

Surface undulation caused by deformation instabilities has been a subject of intensive studies. When a system composed of a thin film bonded to a thick compliant substrate is subjected to in-plane compression, a variety of surface instability morphologies may develop once certain critical states are reached. Such surface patterns may have numerous practical implications in modern flexible devices, self-assembling fabrication, and biomedical engineering [1,2,3,4]. A specific example is photovoltaics and optoelectronics, where improved light trapping [5,6,7,8] and scattering [9] can be achieved with wrinkled surfaces.

For a linear-elastic thin film and soft substrate structure under in-plane biaxial or uniaxial compression, the commonly reported instability patterns include periodic buckles (sinusoidal waves), dimples, checkerboard, herringbone, labyrinth, etc. [10,11,12,13,14,15,16,17]. Although various elastic wrinkling mode transformations may occur upon further straining (e.g., from checkerboard to labyrinth wrinkles under equi-biaxial loading [11, 18]), the surface does not tend to develop more severe forms of topography such as deep folding. On the contrary, the tendency of wrinkles on an inelastic thin film to evolve into folds is well-known, and the process has often been called “wrinkle-to-fold transition” in the literature [19, 20]. Post-instability bifurcations of surface wrinkles in inelastic materials are material and/or geometry dependent [20, 21]. Wrinkles can transform into various localized patterns such as folds, creases (deep sharp valleys), and ridges (tall sharp peaks). They have been studied for viscoelastic and/or hyperelastic film-substrate systems [22,23,24,25,26,27,28,29], and some of the well-established evolution paths were reported in the form of instability phase diagrams [21, 30, 31]. The rate-dependency of the folding process is also well recognized [19, 32, 33]. Similar phenomena have been observed for thin films floating on an incompressible viscous fluidic substrate [34,35,36,37,38,39], as an apparent mechanical analogy exists between the behaviors of liquid and very compliant (and nearly incompressible) solid substrates.

Some theoretical solutions are available to predict the formation of surface instability patterns (e.g., [11, 24]), however, these approaches are usually based on many simplifications and are limited to linear-elastic wrinkles and to the primary instability mode. Well-established closed-form solutions for post-wrinkling bifurcations are unavailable, so numerical simulations are needed. Common numerical techniques have resorted to a muti-step process: a pre-buckling modal analysis followed by a post buckling analysis based on dummy/fictitious force [40,41,42,43] and/or geometric imperfections [28, 43,44,45,46,47,48] to trigger instability and post-instability modes of deformation. The geometric imperfection approaches are essentially based on incorporating a predefined waveform within the model, thus dictating the shape of the instability modes and controlling subsequent bifurcations (e.g., the location of the folds). Similar arguments can be made regarding the location and magnitude of the fictitious force (in fictitious force-based approaches) as it significantly affects the deformation evolution. Moreover, geometric imperfections are hard to implement when the model geometry is complex and therefore advanced computational tools are needed.

The possibility of post-bifurcation wrinkles turning into folds in a plastically deforming thin film resting on a soft substrate has been addressed in very few studies. For instance, the wrinkle-to-crease/fold transition was modeled by Cao et al. [45], where the film layer was assumed to have a smaller plastic yield strength in a narrow region in the middle of the film, thus a single fold was forced to develop locally. This approach essentially dictated the overall shape of the crease and the possibility of formation of multiple creases with a certain interspacing was suppressed. In another study by Yin et al. [49], elastoplastic instabilities were targeted using a finite element model with only shell elements assigned to the film layer. Wrinkle-to-ridge transition in elastoplastic thin films was also attempted numerically [50], under the plane-strain condition, along with the assumption that the substrate is a neo-Hookean material. The numerical results presented in [45, 49, 50] are highly influenced by the geometric imperfections and the multistep procedures as described earlier.

The present study is devoted to 3D finite element simulations of plasticity-mediated deformation instabilities under in-plane uniaxial compression and equi-biaxial loading conditions. The wrinkling instability and subsequent wrinkle-to-fold bifurcations can be triggered continuously via the incorporation of “embedded imperfections” within the model domain [15, 17, 51]. This approach has been employed to capture 3D elastic wrinkling instabilities in a seamless manner [16, 18, 52, 53] and is now expanded into the case when plastic yielding is allowed in the thin-film material. We demonstrate how plastic deformation can affect the thin-film wrinkle geometry and its transformations to folds or ridges under different loading scenarios. The effects of loading and unloading on the evolution of plastic instability patterns are also studied, along with their influences on the overall load–displacement history.

Theory overview

There are a number of theoretical studies addressing uniaxial and equi-biaxial instabilities for a thin film on top of a compliant substrate. Note that closed-form analytical solutions for elastoplastic deformation instabilities are not available, therefore, we only present theories associated with linear-elastic surface wrinkles up through the first bifurcation mode of deformation.

Consider a single-layer thin film bonded to a semi-infinite compliant substrate subjected to in-plane mechanical loading. When the system is subjected to uniaxial compression beyond a critical point, buckling instability in the form of sinusoidal wrinkles, also known as one-dimensional (1D) instability mode, develops on the entire surface. Assuming that the stress is uniform within the film’s thickness, the critical compressive stress associated with the first instability mode is [16, 18]

$${\sigma }_{{\text{cr}}}=\left[\frac{{E}_{{\text{f}}}}{4\left(1-{\nu }_{{\text{f}}}^{2}\right)}\right]{\left[\frac{3\left(1-{\nu }_{{\text{f}}}^{2}\right){E}_{{\text{s}}}}{\left(1-{\nu }_{{\text{s}}}^{2}\right){E}_{{\text{f}}}}\right]}^{2/3}$$
(1)

The critical wrinkling strain at the onset of instability is then [16, 18, 53]

$${e}_{{\text{cr}}}=\frac{1}{4}{\left[\frac{3\left(1-{{\nu }_{{\text{f}}}}^{2}\right){E}_{{\text{s}}}}{\left(1-{{\nu }_{{\text{s}}}}^{2}\right){E}_{{\text{f}}}}\right]}^\frac{2}{3}$$
(2)

which can be obtained by dividing the critical stress in Eq. (1) by the plane-strain modulus of the thin film, namely \({e}_{{\text{cr}}}={\sigma }_{{\text{cr}}}/\left[{E}_{{\text{f}}}/\left(1-{\nu }_{{\text{f}}}^{2}\right)\right]\). In Eqs. (1, 2) \({E}_{{\text{s}}}\) and \({E}_{{\text{f}}}\) are, respectively, Young’s moduli of the substrate and film, and \({\nu }_{{\text{s}}}\) and \({\nu }_{{\text{f}}}\) are, respectively, Poisson’s ratios of the substrate and the film. Note that Eqs. (1, 2) are only a function of elastic properties of the film and substrate.

Upon reaching the critical state, the wavelength of the wrinkles is analytically expressed as [16, 18]

$${\lambda }_{{\text{cr}}}={\left({\lambda }_{{\text{cr}}}\right)}_{1{\text{D}}}=2\pi {t}_{{\text{f}}}{\left[\frac{\left(1-{\nu }_{{\text{s}}}^{2}\right){E}_{{\text{f}}}}{3\left(1-{\nu }_{{\text{f}}}^{2}\right){E}_{{\text{s}}}}\right]}^{1/3}$$
(3)

where \({t}_{{\text{f}}}\) is the thickness of the thin film. Under equi-biaxial compression, the formation of the square-checkerboard pattern at the first bifurcation point was analytically predicted, and the critical wavelength associated with this deformation mode, \({\left({\lambda }_{{\text{cr}}}\right)}_{{\text{Cb}}}\), was derived as [18, 19]

$${\left({\lambda }_{{\text{cr}}}\right)}_{{\text{Cb}}}=\sqrt{2 }{\left({\lambda }_{{\text{cr}}}\right)}_{1{\text{D}}}=2\sqrt{2}\pi {t}_{{\text{f}}}{\left[\frac{\left(1-{\nu }_{{\text{s}}}^{2}\right){E}_{{\text{f}}}}{3\left(1-{\upsilon }_{{\text{f}}}^{2}\right){E}_{{\text{s}}}}\right]}^{1/3}$$
(4)

In addition, the wave’s amplitude, \(A\), can be written in a general form as

$$A=\Psi {\left(\frac{e}{{e}_{{\text{cr}}}}-1\right)}^{1/2}$$
(5)

where \(e/{e}_{{\text{cr}}}\) is the applied compressive strain normalized by the critical value, and the parameter \(\Psi\) is a function of thickness and Poisson’s ratio of the film layer, with \(\Psi\) = \({t}_{{\text{f}}}\) for the sinusoidal 1D mode and \(\psi = t_{{\text{f}}} \left( {\sqrt {{\raise0.5ex\hbox{$\scriptstyle 8$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {\left[ {\left( {3 - \upsilon_{{\text{f}}} } \right)\left( {1 + \upsilon_{{\text{f}}} } \right)} \right]}$}}} } \right)\) for the square-checkerboard mode [17, 19]. Once the instability point is reached, the amplitude continues to increase as the applied strain increases. The in-plane elastic surface pattern stays in place before any possible subsequent bifurcation point is reached.

Numerical model setup

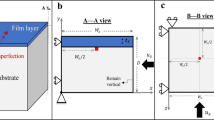
Figure 1a shows the overall geometry of the problem domain, which consists of a thin film above a thick substrate. The rectangular block has a square shape in the x–z plane with the dimensions of \({W}_{x}={W}_{z}=7{\lambda }_{{\text{cr}}}\), Fig. 1c. The overall depth is set as \(D=5{\lambda }_{{\text{cr}}}\) (Fig. 1b), which is sufficiently thick to avoid dependency of the numerical solutions on the model depth [51, 53]. The domain size is deliberately scaled by the critical wavelength of the 1D mode (\({\lambda }_{{\text{cr}}}\) in Eq. (3)) to accommodate both primary elastic modes of deformation instability under uniaxial and equi-biaxial loading (note that \(7{\lambda }_{1{\text{D}}}\cong 5{\lambda }_{{\text{Cb}}}\) based on Eqs. (3, 4)). A constant film thickness of \({t}_{{\text{f}}}=0.1 \mathrm{\mu m}\) is presumed in all the simulations. The model system uses the P3HT:PCBM organic semiconductor thin film bonded to the highly compliant PDMS elastomeric substrate. According to some experimental references of P3HT-based materials [54,55,56,57,58], the mechanical behavior may be considered as isotropic elastic-perfectly plastic (as schematically shown in Fig. 1a, right-hand side), with Young’s modulus \({E}_{{\text{f}}}=7300\) MPa, Poisson’s ratio \({\nu }_{{\text{f}}}=0.35\), and plastic yield strength \({\sigma }_{{\text{y}}}=40\) MPa. The PDMS substrate is taken as isotropic linear-elastic, with Young’s modulus \({E}_{{\text{s}}}=2.97\) MPa [59] and Poisson’s ratio 0.495 (set to be slightly smaller than 0.5 to mimic the nearly incompressible condition but to avoid potential numerical convergence problems). Note that the focus of this study is on the effects of thin-film plasticity, so the constitutive behavior of the substrate is kept as the simple elastic form. This treatment also enables direct comparisons with reliable analytical solutions as presented below.

Figure 1
figure 1

a–c Schematics of the problem domain, boundary conditions, and directions of the applied displacement. The stress–strain response for the thin film material is also schematically shown in (a).

Full size image

The static simulations were performed under displacement control with geometric nonlinearity (large deformation analyses). The displacement increments were small enough to eliminate potential increment size dependencies of the numerical solutions [51]. Twenty-noded continuum brick elements were used throughout. The mesh was sufficiently fine to avoid mesh-dependent solutions. (Part of our comprehensive convergence studies are described in the next section.) The mesh distribution is structured in the film layer (four layers of uniformly distributed elements) and in the substrate the element size gradually increases from the interface to the bottom boundary. The simulations were performed using the commercial finite element software ABAQUS (Versions 2017 and 2022, standard solver, Dassault Systems Simulia Corp., Johnston, RI, USA). All calculations utilized the parallelization approach with the message passing interface (MPI) featuring two computing nodes, 64 Intel Xeon Gold CPUs, in order to efficiently solve the large-scale three-dimensional instability problems well into the post-wrinkling stages.

Figure 1b and c also depicts the boundary conditions used in the simulations. The roller condition was imposed on planes \(x=0\), \(y=0\), and \(z=0\). All the nodes on the boundaries \(x= {W}_{x}\) and \(z= {W}_{z}\) are constrained to remain vertical (parallel to y-axis) during deformation [60]. The film’s surface \(y= D\) is traction-free. A uniform compressive displacement (or strain) is applied either uniaxially in the x-direction (at plane \(x={W}_{x}\)) or equi-biaxially in both the x and z directions (at planes \(x= {W}_{x}\) and \(z= {W}_{z}\)) as discussed with more details in the following section. The model is essentially a representative volume of a large periodic structure as in our earlier studies [18, 53]. Furthermore, as schematically shown in Fig. 1, only one embedded imperfection was employed to help trigger the instability modes, and it was placed exactly in the middle of the x–z plane immediately below the film-substrate interface to ensure the symmetry of the periodic cell. While the imperfection is a regular finite element at the top center of the substrate, it carries the properties of the film material. Perfect bonding is still maintained across the interface. The imperfection is square shaped in the x–z plane, with a constant out-of-plane thickness of 0.5 \({t}_{{\text{f}}}\). Based on the current setup, the numerical solutions are independent of the imperfection size as demonstrated in [16]. The numerically predicted elastic–plastic wrinkling and folding patterns pertain to this unit-cell approach in the vicinity of a single imperfection.

Results and discussion

We start with a brief model verification study to assess the numerical models and mesh convergence. The model is perfectly flat before loading as illustrated in Fig. 2a, and representative images of the numerical solutions associated with the converged mesh size under uniaxial and equi-biaxial loading are also shown. Two analyses were conducted for each loading: one with a linear-elastic film material (no plastic yielding) and the other with an elastoplastic film layer as described in Sect. "Numerical model setup". Based on our comprehensive convergence studies, the mesh density of 25 elements per elastic critical wavelength (\({\lambda }_{{\text{cr}}}\) as defined in Eq. (3)) in the x and z directions, with also other distribution features mentioned in Sect. "Numerical model setup", is sufficient to achieve mesh-insensitive numerical results.

Figure 2
figure 2

a Schematics showing the numerically obtained instability evolution from a flat surface to 1D sinusoidal and square-checkerboard patterns under, respectively, uniaxial and equi-biaxial compression. b–c Amplitude, A, of the highlighted wave normalized by the film’s thickness, \({t}_{{\text{f}}}\), plotted as a function of normalized applied compressive strain (\({e}_{{\text{xx}}}/{e}_{{\text{cr}}}\)), for the cases of b uniaxial and c equi-biaxial loading.

Full size image

According to the current material property definitions, the critical elastic wrinkling stress can be calculated from Eq. (1) as \({\sigma }_{{\text{cr}}}=26.258 {\text{MPa}}\). As a consequence, \({\sigma }_{{\text{cr}}}<{\sigma }_{{\text{y}}}\) so the elastic instability occurs earlier than plastic yielding. The primary (elastic) instability patterns obtained under uniaxial and equi-biaxial compression are shown in Fig. 2a. Note that both the 1D sinusoidal waves and square-checkerboard pattern have the wavelengths fully consistent with the elastic instability theories [11, 16]. Figure 2b and c shows the simulated evolution of wrinkle amplitude as a function of applied compressive strain for the cases of uniaxial loading and equi-biaxial loading, respectively. The amplitude (A) is normalized by the initial film thickness (tf), and the compressive strain (exx) is normalized by the critical strain for elastic instability (ecr). The presentation includes the behaviors of films without and with the built-in plastic yield strength, as well as the theoretical elastic response (from Eq. (5)). Note that the amplitude is obtained by tracking a specific wave near the lower-right corner as highlighted in Fig. 2a. As can be seen, the elastic and elastoplastic numerical results coincide with each other from pre-instability to after the primary (elastic) instability. The response is also in agreement with the elastic analytical solution.

For the case of uniaxial loading (Fig. 2b), the deviation of the elastoplastic response from its elastic counterpart is the onset of plastic instability (the start of the folding process, as discussed below). For the case of equi-biaxial loading (Fig. 2c), the deviation of the elastoplastic response from the elastic theory is also where the plasticity-mediated pattern transformation starts, and in this case, there is a sudden reduction in amplitude. The simulated elastic response displays an early amplitude drop, which is the secondary instability point with an elastic mode change (from checkerboard to other elastic surface patterns as presented in our earlier work [18]). It is worth emphasizing that, using the present embedded imperfection approach, all simulations are “direct” in that the entire deformation history is obtained in only one simulation step (run). Commonly used numerical approaches have resorted to a multistep process, involving a pre-buckling modal analysis followed by a post buckling analysis based on, e.g., geometric imperfections [28, 43,44,45,46,47,48] to trigger instability and post-instability modes of deformation. This traditional methodology essentially builds a predefined waveform into the structure after the first modal analysis, thus dictating the wrinkling pattern and restricting direct predictions of subsequent instability transformations. Using our current simulation technique, neither a multistep procedure nor any other interruption is needed. Results presented in this paper demonstrate its capability in not only triggering elastic instability but capturing subsequent pattern changes influenced by plastic yielding in a robust manner.

Figure 3 shows representative snapshots of surface features during an entire course of uniaxial compression, including the loading and unloading phases. The magnitudes of applied compressive strain corresponding to the images are also indicated. The simulation starts from a stress-free flat surface, turning into sinusoidal waves after reaching primary elastic instability. With plastic yielding occurring upon further straining, the instability pattern gradually transforms into deeper folds with a wider spacing. In the same simulation run, an unloading process was also included. It is evident in Fig. 3 that, during unloading, while the amplitude becomes smaller, the folds remain in place. The overall pattern is retained when the applied strain is reduced to zero, signifying permanent deformation caused by plastic deformation. This outcome is different from the case of pure elastic instability where, upon full unloading, wrinkles completely disappear with the surface becoming flat again [16, 18, 52, 53].

Figure 3
figure 3

Evolution of elastoplastic instability under uniaxial compression, during the loading and unloading phases obtained from the direct numerical simulation.

Full size image

The same type of loading–unloading history under equi-biaxial compression is presented in Fig. 4. During loading, the elastic square-checkerboard pattern forms, but wrinkle-to-fold transition takes place upon plastic yielding of the thin film. The folds manifest themselves as ridges separated by larger distances (each with one tall peak flanked by two valleys). A distinct square shape along the 45° directions thus evolves as equi-biaxial compression progresses. Upon unloading, the square ridges tend to reduce their height but the pattern remains when the biaxial compressive strain is completely removed. This is again the plasticity-induced permanent deformation in the form of surface instability.

Figure 4
figure 4

Evolution of elastoplastic instability under equi-biaxial compression, during the loading and unloading phases obtained from the direct numerical simulation.

Full size image

It is worth mentioning that, in both uniaxial and biaxial loading, once plastic folds emerge on the surface, the overall configuration stays qualitatively unchanged even after significant straining of \({e}_{{\text{xx}}}/{e}_{{\text{cr}}}\cong 4.0\) and beyond. The same surface pattern persists during the entire course of strain relief. Figure 5a and b shows the final patterns at the end of loading (left) and unloading (right), for the cases of uniaxial and equi-biaxial compression, respectively. Side and top views obtained from the simulations are included.

Figure 5
figure 5

Side and top views of the plastic folding patterns at the end of loading (left) and unloading (right) under a uniaxial and b equi-biaxial compression.

Full size image

The macroscopic deformation response extracted from the numerical output is now examined. While the applied strain and overall reaction force are both compressive, they are presented as positive here. The uniaxial and equi-biaxial load-strain responses are shown in Fig. 6a and b, respectively. In each loading mode, results from three different analyses are included for comparison: elastoplastic film (same simulations shown in Figs. 3 and 4), pure elastic film (with no plastic yielding), and a separate analysis of elastoplastic film model without any embedded imperfection. Note the last scenario does not initiate any elastic or plastic instability, and the thin film will remain flat regardless of the extent of the applied deformation. It can be seen that the elastic response follows the regular linear behavior initially, then a sudden change in slope signifies the onset of elastic instabilities (sinusoidal wrinkles in Fig. 6a and square-checkerboard in Fig. 6b). Upon unloading, the load-strain response follows the original path and is fully recoverable.

Figure 6
figure 6

Reaction force in x-direction (Fx) plotted as a function of applied strain (exx) for the simulations under a uniaxial and b equi-biaxial loading.

Full size image

In the case of elastoplastic thin films (with the embedded imperfection to trigger instabilities), the first change in slope is the same as the elastic behavior. Subsequent plastic yielding results in the wrinkle-to-fold transformation, leading to deviations from the second linear portion of the elastic curve with lower overall loads. When unloading commences, the load-strain response does not follow the prior path. Deformation is irrecoverable and, as evidenced in Fig. 6a and b, a compressive strain remains as the load is reduced to zero. This permanent dimensional change is associated with the residual thin-film deformation patterns presented in Figs. 3 and 4.

Also included as a reference in Fig. 6a and b is the elastoplastic case without any imperfection. No instability appears in the simulations, and the change in slope during loading is a consequence of uniform yielding in the thin film. Although the film is assumed to be elastic-perfectly plastic, the overall load shows an increasing trend after yielding because it includes contributions from both the film material and the substrate (which is purely elastic). Upon unloading, the reduction in load follows the initial elastic slope as in all “regular” materials without instability. The significant irrecoverable plastic strain at the end of load removal is apparent.

It is worth pointing out that, in Fig. 6b, a slight discrepancy in the loading and unloading curves in the pure elastic model can be observed. This is caused by artificial viscous damping used in the numerical implementation in the equi-biaxial loading simulations [18]. During the course of equi-biaxial loading, frequent elastic mode transformations take place, and using damping ensures the stability of numerical solutions [18, 50], which leads to a slight history dependency. It should also be noted that artificial damping is only added to the equi-biaxial elastic model; all the other simulations presented in this paper were conducted without the use of damping. The corresponding damping factor(s) were calculated by the finite element program via the automatic stabilization algorithm performed iteratively in each analysis increment. The ratio of the energy dissipated by viscous damping and the total strain energy is the only user-defined parameter in this approach, and it is 5% (software default) in this study to ensure convergence without generating damping-dependent solutions [18, 53].

As described above, the model system used in this study is such that the elastic wrinkling instability emerges before the film yields (\({\sigma }_{{\text{cr}}}<{\sigma }_{y}\)). The focus of this study is thus on how elastic wrinkles may be modified by subsequent plastic yielding of the thin film. For different material systems involving a thin film attached to a compliant substrate, the possibility of \({\sigma }_{y}<{\sigma }_{{\text{cr}}}\) exists, meaning that film yielding will occur before the primary elastic instability. This is a more sophisticated scenario since no theoretical solution is available in the literature for numerical model verification and calibration. How the detailed plastic deformation parameters may affect the initiation and evolution of the instability patterns, along with their interplay with the distribution of preexisting imperfections and possible inelastic behavior of the substrate, present a wide range of possibilities for further explorations.

Conclusions

This paper presents a systematic 3D numerical study on surface instabilities in thin film/compliant substrate systems under in-plane uniaxial and biaxial compression. Attention is devoted to the formation and transformation of wrinkle patterns influenced by plastic yielding of the thin film. The embedded imperfection technique developed earlier for the elastic wrinkling behavior was successfully employed to model plastic instabilities, generating new insights into the less common forms of surface morphologies. Under uniaxial loading, the sinusoidal elastic wrinkles undergo the wrinkle-to-fold transition when yielding starts. The resulting folds are spaced farther apart than the initial wrinkles. With equi-biaxial loading, the initial checkerboard islands turn into continuous tall ridges along the 45° directions forming a square pattern. In both loading modes, the surface patterns were only partially relieved upon complete unloading. This plasticity-induced permanent pattern does not exist in pure elastic systems where the configuration change is fully recoverable. The overall load-strain response can be directly extracted from the simulation output to correlate with the evolving deformation features.