Abstract
The Butler equation is extended to model equilibrium grain boundary (GB) energy and the equilibrium GB composition of a polycrystal, as a function of the following state parameters: bulk composition, temperature, pressure and the five degrees of freedom of the GB. In the simplest case of an ideal solution and equal atomic sizes of the components, the Butler equation reduces back to the well-known McLean equation of GB segregation. When the components repulse each other in the solid solution, grain boundary segregation transition (GBST) appears below the critical temperature of the bulk solid miscibility gap. The GBST line is a new equilibrium line in equilibrium phase diagrams. This new model is demonstrated for copper (Cu) segregation to the GBs in nickel (Ni) and for the phosphorous (P) segregation to the GBs in bcc iron (Fe). The GBST line appears in the Ni-rich (Fe-rich) corner of the Ni–Cu (Fe–P) phase diagram in coordinates of bulk Cu (P) mole fraction vs temperature at fixed pressure. The mole fraction of the solute (Cu or P), corresponding to the GBST line steadily increases with temperature. At a lower solute content (Cu or P), or at a higher temperature compared to the GBST line, the GB is composed mostly of the solvent atoms (Ni or Fe). Contrariwise, at a higher solute content (Cu or P), or at a lower temperature compared to the GBST line, the GB is composed mostly of the solute atoms (Cu or P). These low-segregation and high-segregation states of the GB are transformed into each other via a reversible first-order GBST. This latter process takes place when the GBST line is crossed by changing the bulk composition or the temperature. The results, theoretically estimated, are in agreement with earlier experimental results.









Similar content being viewed by others
References
Straumal AB, Yardley VA, Straumal BB, Rodin AO (2015) Influence of the grain boundary character on the temperature of transition to complete wetting in the Cu-In system. J Mater Sci 50:4762–4771. doi:10.1007/s10853-015-9025-x
Kuzmina M, Ponge D, Raabe D (2015) Grain boundary segregation engineering and austenite reversion turn embrittlement into toughness: example of a 9 wt.% medium Mn steel. Acta Mater 86:182–192. doi:10.1016/j.actamat.2014.12.021
Wharry JP, Was GS (2014) The mechanism of radiation-induced segregation in ferritic martensitic alloys. Acta Mater 65:42–55
Hegedus Z, Gubicza J, Kawasaki M, Chinh NQ, Labar JL, Langdon TG (2013) Stability of the ultrafine-grained microstructure in silver processed by ECAP and HPT. J Mater Sci 48:4637–4645. doi:10.1007/s10853-012-7124-5
Menyhard M (1992) Effect of phosphorus on non-brittle grain boundaries of iron. Scr Metall Mater 26:1695–1700
Lejcek P (2010) Grain boundary segregation in metals, vol 136., Springer Series in Materials ScienceSpringer, Berlin
Gibbs JW (1875–1878) On the equilibrium of heterogeneous substances. Trans Conn Acad Arts Sci 3:108–248 and 343–524
Langmuir I (1918) The adsorption of gases on plate surface of glass, mica and platinum. J Am Chem Soc 40:1361–1403
McLean D (1957) Grain boundaries in metals. Clarendon Press, Oxford
Fowler RH, Guggenheim EA (1939) Statistical thermodynamics. Cambridge University Press, Cambridge
Guttmann M (1975) Equilibrium segregation in ternary solutions: a model for temper embrittlement. Surf Sci 53:213–227
Seah MP, Lea C (1975) Surface segregation and its relation to grain boundary segregation. Philos Mag 31:627–645
Wynblatt P, Ku RC (1977) Surface energy and solute strain energy effects in surface segregation. Surf Sci 65:511–531
Miedema AR (1978) Surface energies of solid metals. Z Metallkunde 69:287–292
Kumar V (1981) Chemical composition at alloy surfaces. Phys Rev B 23:3756
Mezey LZ, Giber J (1985) New, simple rules of interface segregation. Surf Sci 162:514–518
Mukherjee S, Morán-López JL (1987) Theory of surface segregation in transition metal alloys. Surf Sci 188:L742–L748
Luthra KL, Briant CL (1988) Thermodynamics of segregation in alloys. Metall Trans A 19:2091–2098
Sutton AP, Balluffi RF (1995) Interfaces in crystalline materials. Clarendon, Oxford, p 349
Berthier F, Creuze J, Tetot R, Legrand B (2002) Multilayer properties of superficial and intergranular segregation isotherms: a mean-field approach. Phys Rev B 65:195413
Esin VA, Souhar Y (2014) Solvent grain boundary diffusion in binary solid solutions: a new approach to evaluate solute grain boundary segregation. Philos Mag 94:4066–4079
Butler JAV (1932) The thermodynamics of the surfaces of solutions. Proc R Soc A135:348–375
Hoar TP, Melford DA (1957) The surface tension of binary liquid mixtures: lead + tin and lead + indium alloys. Trans Faraday Soc 53:315–326
Monma K, Suto H (1961) Thermodynamics of surface tension. J Jpn Inst Met 25:65–68
Hondros ED (1980) Rule for surface enrichment in solutions. Scr Metall 14:345–348
Speiser R, Poirier DR, Yeum K (1987) Surface tension of binary liquid alloys. Scr Metall 21:687–692
Hajra JP, Lee HK, Frohberg MG (1991) Calculation of the surface tension of liquid binary systems from the data of the pure components and the thermodynamic infinite dilution values. Z Metallkunde 82:603–608
Tanaka T, Hack K, Iida T, Hara S (1996) Application of a thermodynamic database to the evaluation of surface tensions of molten alloys, salt mixtures and oxide mixtures. Z Metallkunde 87:380–389
Gasior W, Moser Z, Pstrus J (2001) Density and surface tension of the Pb-Sn liquid alloys. J Phase Equilib 22:20–25
Liu XJ, Inohana Y, Takaku Y, Ohnuma I, Kainuma R, Ishida K, Moser Z, Gasior W, Pstrus J (2002) Experimental determination and thermodynamic calculation of the phase equilibria and surface tension in the Sn-Ag-In system. J Electron Mater 31:1139–1151
Picha R, Vrestal J, Kroupa A (2004) Prediction of alloy surface tension using a thermodynamic database. Calphad 28:141–146
Lee J, Park J, Tanaka T (2009) Effects of interaction parameters and melting points of pure metals on the phase diagrams of the binary alloy nanoparticle systems: a classical approach based on the regular solution model. Calphad 33:377–381
Brillo J, Plevachuk Y, Egry I (2010) Surface tension of liquid Al-Cu-Ag ternary alloys. J Mater Sci 45:5150–5157. doi:10.1007/s10853-010-4512-6
Garzel G, Janczak-Rusch J, Zabdyr L (2012) Reassessment of the Ag-Cu phase diagram for nanosystems including particle size and shape effect. Calphad 36:52–56
Sopousek J, Vrestal J, Pinkas J, Broz P, Bursik J, Styskalik A, Skoda D, Zobac O, Lee J (2014) Cu–Ni nanoalloy phase diagram—prediction and experiment. Calphad 45:33–39
Kambolov DA, Kashezhev AZ, Kutuev RA, Ponegev MKh, Sozaev VA, Kh Shermetov A (2014) Polytherms of the density and surface tension of a zinc-aluminium-molybdenum-magnesium melt. Bull Russ Acad Sci Phys 78:785–787
Plevachuk Y, Sklyarchuk V, Eckert S, Gerbeth G, Novakovic R (2014) Thermophysical properties of the liquid Ga–In–Sn eutectic alloy. J Chem Eng Data 59:757–763
Costa C, Delsante S, Borzone G, Zivkovic D, Novakovic R (2014) Thermodynamic and surface properties of liquid Co–Cr–Ni alloys. J Chem Thermodyn 69:73–84
Kang YB (2015) Relationship between surface tension and Gibbs energy, and application of constrained Gibbs energy minimization. Calphad 50:23–31
Kaptay G (2015) On the partial surface tension of components of a solution. Langmuir 31:5796–5804
Kaptay G (2012) On the interfacial energy of coherent interfaces. Acta Mater 60:6804–6813
Brillo J, Schmid-Fetzer R (2014) A model for the prediction of liquid–liquid interfacial energies. J Mater Sci 49:3674–3680. doi:10.1007/s10853-014-8074-x
Weltsch Z, Lovas A, Takács J, Cziráki Á, Tóth A, Kaptay G (2013) Measurement and modelling of the wettability of graphite by a silver-tin (Ag-Sn) liquid alloy. Appl Surf Sci 268:52–60
Kaptay G (2005) A method to calculate equilibrium surface phase transition lines in monotectic systems. Calphad 29:56–67 and p. 262
Mekler C, Kaptay G (2008) Calculation of surface tension and surface phase transition line in binary Ga-Tl system. Mater Sci Eng A 495:65–69
Sándor T, Mekler C, Dobránszky J, Kaptay G (2013) An improved theoretical model for A-TIG welding based on surface phase transition and reversed Marangoni flow. Metall Mater Trans 44A:351–361
Vegh A, Mekler C, Kaptay G (2013) A unified theoretical framework to model bulk, surface and interfacial thermodynamic properties of immiscible liquid alloys. Mater Sci Forum 752:10–19
Dillon SJ, Tang M, Carter WC, Harmer MP (2007) Complexion: a new concept for kinetic engineering in materials science. Acta Mater 55:6208–6218
Carter WC, Baram M, Drozdov M, Kaplan WD (2010) Four questions about triple lines. Scr Mater 62:894–898
Straumal BB, Baretzky B, Kogtenkova OA, Straumal AB, Sidorenko AS (2010) Wetting of grain boundaries in Al by the solid Al3Mg2 phase. J Mater Sci 45:2057–2061. doi:10.1007/s10853-009-4014-6
Baram M, Chatain D, Kaplan WD (2011) Nanometer-thick equilibrium films: the interface between thermodynamics and atomistics. Science 332:206–209
Kaptay G (2012) Nano-Calphad: extension of the Calphad method to systems with nano-phases and complexions. J Mater Sci 47:8320–8335. doi:10.1007/s10853-012-6772-9
Kaplan WD, Chatain D, Wynblatt P, Carter WC (2013) A review of wetting versus adsorption, complexions, and related phenomena: the rosetta stone of wetting. J Mater Sci 48:5681–5717. doi:10.1007/s10853-013-7462-y
Frolov T, Olmsted DL, Asta M, Mishin Y (2013) Structural phase transformations in metallic grain boundaries. Nat Comm 4:1899
Cantwell PR, Tang M, Dillon SJ, Luo J, Rohrer GS, Harmer MP (2014) Grain boundary complexions (Overview No. 152). Acta Mater 62:1–48
Frolov T (2014) Effect of interfacial structural phase transformations on the coupled motion of grain boundaries: a molecular dynamics study. Appl Phys Lett 104:211905
Hondros ED, Seah MP (1977) The theory of grain boundary segregation in terms of surface adsorption analogues. Metal Trans A 8A:1363–1371
Guttmann M (1977) Grain boundary segregation, two dimensional compound formation and precipitation. Metal Trans A 8A:1383–1401
Rabkin EI, Shvindlerman LS, Straumal BB (1990) Wetting and premelting phase transitions in 43° (100) tilt grain boundaries in Fe-5 at.% Si. Coll Phys 51:599–603
Rabkin EI, Shvindlerman LS, Straumal BB (1991) Grain boundaries: phase transitions and critical phenomena. Intern J Mod Phys B 5:2989–3028
Bokstein BS, Rodin AO, Smirnov AN (2004) Connection between Fe grain boundary segregation in Al and phase formation in the bulk. Z Metallkde 95:953–955
Wynblatt P, Chatain D (2006) Anisotropy of segregation at grain boundaries and surfaces. Metall Mater Trans 37A:2595–2620
Lejcek P, Hofmann S (2008) Thermodynamics of grain boundary segregation and applications to anisotropy, compensation effect and prediction. Crit Rev Solid State Mater Sci 33:133–163
Straumal BB (2003) Grain boundary phase transitions (in Russian). Nauka, Moscow
Weismüller J (1993) Alloy effects in nanostructures. Nanostruct Mater 3:261–272
Gleiter H (2000) Nanostructured materials: basic concepts and microstructure. Acta Mater 48:1–29
Kirchheim R (2002) Grain coarsening inhibited by solute segregation. Acta Mater 50:413–419
Koch CC (2007) Structural nanocrystalline materials: an overview. J Mater Sci 42:1403–1414. doi:10.1007/s10853-006-0609-3
Pellicer E, Varea A, Sivaraman KM, Pane S, Surinach S, Baro MD, Nogues J, Nelson BJ, Sort J (2011) Grain boundary segregation and interdiffusion effects in the nickel-copper alloys: an effective means to improve the thermal stability of nanocrystalline nickel ACS Appl. Mater Interfaces 3:2265–2274
Chookajorn T, Murdoch HA, Schuh CA (2012) Design of stable nanocrystalline alloys. Science 23:951–954
Saber M, Koch CC, Scattergold RO (2015) Thermodynamic grain size stabilization models: overview. Mater Res Lett 3:65–75
Lewis GN (1907) Outlines of a new system of thermodynamic chemistry. Proc Am Acad Arts Sci 43:259–293
Saunders N, Miodownik AP (1998) CALPHAD, a comprehensive guide. Pergamon, London
Lukas HL, Fries SG, Sundman B (2007) Computational thermodynamics. The Calphad method. Cambridge University Press, Cambridge
Iida T, Guthrie RIL (1993) The physical properties of liquid metals. Clarendon Press, Oxford
Kaptay G (2008) A unified model for the cohesive enthalpy, critical temperature, surface tension and volume thermal expansion coefficient of liquid metals of bcc, fcc and hcp crystals. Mater Sci Eng A 495:19–26 and 501:255
Tyson WR, Miller WA (1977) Surface free energies of solid metals: estimation from liquid surface tension measurements. Surf Sci 62:267–276
Kaptay G (2005) Modeling interfacial energies in metallic systems. Mater Sci Forum 473–474:1–10
Scott GD (1960) Packing of equal spheres. Nature 188:908–909
Topuridze NI, Hantadze DV (1978) On a geometric factor of the excess volume of a solution (in Russian). Zh Fiz Himii LII:81–84
Kaptay G (2014) On the abilities and limitations of the linear, exponential and combined models to describe the temperature dependence of the excess Gibbs energy of solutions. Calphad 44:81–94
Wandelt K, Brundle CR (1981) Evidence for crystal-face specificity in surface segregation of CuNi alloys. Phys Rev Lett 46:1529–1532
Abrikosov IA, Skriver HL (1993) Self-consistent linear-muffin-tin-orbitals coherent-potential technique for bulk and surface calculations: Cu-Ni, Ag-Pd, and Au-Pt random alloys. Phys Rev B 47:16532–16541
Ahmed J, Ramanujachary KV, Lofland SE, Furiato A, Gupta G, Shivaprasad SM, Ganguli AK (2008) Bimetallic Cu–Ni nanoparticles of varying composition (CuNi3, CuNi, Cu3Ni). Colloid Surf A 331:206–212
Kolobov YuR, Grabovetskaya GP, Ivanov MB, Zhilayev AP, Valiev RZ (2001) Grain boundary diffusion characteristics of nanostructured nickel. Scr Mater 44:873–878
Bokstein BS, Bröse HD, Trusov LJ, Khvostantseva TP (1995) Diffusion in nanocrystalline nickel. NanoStruct Mater 6:873–876
Baró MD, Kolobov YuV, Ovidko IA, Schaefer HE, Straumal BB, Valiev RZ, Alexandrov IV, Ivanov M, Reimann K, Reizis AB, Surinas S, Zhilyaev AP (2001) Diffusion and related phenomena in bulk nanostructured materials. Rev Adv Mater Sci 2:1–43
Massalski TB (ed) (1990) Binary alloy phase diagrams, 2nd edn. ASM International, Materials Park
Miettinen J (2003) Thermodynamic description of the Cu-Ni-Sn system at the Cu-Ni side. Calphad 27:309–318
Mezbahul-Islam M, Medraj M (2015) Thermodynamic modeling of Cu-Ni-Y system coupled with key experiments. Mater Chem Phys 153:32–47
Kaptay G (2004) A new equation for the temperature dependence of the excess Gibbs energy of solution phases. Calphad 28:115–124
Kaptay G (2012) On the tendency of solutions to tend toward ideal solutions at high temperatures. Metall Mater Trans A 43:531–543
Hillert M, Jarl M (1978) A model for alloying effects in ferromagnetic metals. Calphad 2:227–238
Dinsdale AT (1991) SGTE data for pure elements. Calphad 15:317–425
Mezey LZ, Giber J (1982) The surface free energies of solid chemical elements: calculation from internal free enthalpies of atomization. Jpn J Appl Phys 21:1569–1571
Pearson WB (1958) A handbook of lattice spacings and structures of metals and alloys. Pergamon Press, London
Kaptay G (2015) Approximated equations for molar volumes of pure solid fcc metals and their liquids from zero Kelvin to above their melting points at standard pressure. J Mater Sci 50:678–687. doi:10.1007/s10853-014-8627-z
Wynblatt P, Liu Y (1992) Two-dimensional phase transitions associated with surface miscibility gaps. J Vac Sci Technol 10:2709–2717
Predel B (1991–1997) Phase equilibria, crystallographic and thermodynamic data of binary alloys, volume 5 of group IV of Landolt-Börnstein Handbook. Springer, Berlin
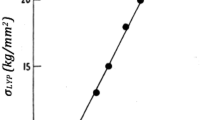
Hondros ED (1965) The influence of phosphorus in dilute solid solution on the absolute surface and grain boundary energies of iron. Proc R Soc 286:479–498
Erhart H, Grabke HJ (1981) Equilibrium segregation of phosphorus at grain boundaries of Fe-P, Fe-C-P, Fe-Cr-P and Fe-Cr-C-P alloys. Metal Sci 15:401–408
Briant CL (1985) Grain boundary segregation of phosphorus in 304L stainless steel. Metal Trans 16A:2061–2062
Menyhard M, McMahon CJ Jr (1989) On the effect of molybdenum in the embrittlement of phosphorus-doped iron. Acta metal 31:2287–2295
Lejcek P (1994) Characterization of grain boundary segregation in an Fe-Si alloy. Anal Chim Acta 297:165–178
Lejcek P (1994) On the thermodynamic description of grain boundary segregation in polycrystals. Mater Sci Eng A 185:109–114
Cowan JR, Evans HE, Jones RB, Bowen P (1998) The grain-boundary segregation of phosphorus and carbon in an Fe–P–C alloy during cooling. Acta Mater 46:6565–6574
Gurovich BA, Kuleshova EA, YaI Shtrombakh, Zabusov OO, Krasikov EA (2000) Intergranular and intragranular phosphorus segregation in Russian pressure vessel steels due to neutron irradiation. J Nucl Mater 279:259–272
Sevc PE, Janovec J, Lejcek P, Zahumensky P, Blach J (2002) Thermodynamics of phosphorus grain boundary segregation in 17Cr12Ni austenitic steel. Scr Mater 46:7–12
Li C, Williams DB (2003) Anisotropy of P grain boundary segregation in a rapidly solidified Fe-0.6 wt% P alloy. Interface Sci 11:461–472
Janovec J, Vyrostkova A, Sevc P, Robinson JS, Svoboda M, Krestankova J, Grabke HJ (2003) Precipitation related anomalies in kinetics of phosphorus grain boundary segregation in low alloy steels. Acta Mater 51:4025–4032
Hurchand H, Kenny SD, Smith R (2005) The interaction of P atoms and radiation defects with grain boundaries in an α-Fe matrix. Nucl Instrum Meth Phys Res 229:92–102
Nishiyama Y, Onizawa K, Suzuki M, Anderegg JW, Nagai Y, Toyama T, Hasegawa M, Kameda J (2008) Effects of neutron-irradiation-induced intergranular phosphorus segregation and hardening on embrittlement in reactor pressure vessel steels. Acta Mater 56:4510–4521
Yuasa M, Mabuchi M (2011) First-principles study on enhanced grain boundary embrittlement of iron by phosphorus segregation. Mater Trans 52:1369–1373
Kim BJ, Kasada R, Kimura A, Tanigawa H (2012) Evaluation of grain boundary embrittlement of phosphorus added F82H steel by SSTT. J Nucl Mater 421:153–159
Wang K, Yang C, Si H (2013) Effect of non-equilibrium grain-boundary segregation of phosphorus on the intermediate-temperature ductility minimum of an Fe–17Cr alloy. Mater Sci Eng A 587:228–232
Gurovich B, Kuleshova E, Zabusov O, Fedotova S, Frolov A, Saltykov M, Maltsev D (2013) Influence of structural parameters on the tendency of VVER-1000 reactor pressure vessel steel to temper embrittlement. J Nucl Mater 435:25–31
Ohtani H, Hanaya N, Hasebe M, Teraoka SI, Abe M (2006) Thermodynamic analysis of the Fe-Ti-P ternary system by incorporating first-principles calculations into the CALPHAD approach. Calphad 30:147–158
Emsley J (1989) The elements. Clarendon Press, Oxford
Touloukian YS, Kirby RK, Taylor RE, Lee TYR (1977) Thermal expansion. IFI/Plenum, New York
Acknowledgements
This work was financed by project OTKA K101781 of the Hungarian Academy of Sciences. The results were achieved within the Center of Applied Materials Science and Nano-Technology at the University of Miskolc and within the TÁMOP-4.2.2.A-11/1/KONV-2012-0019 and TÁMOP-4.2.2.A-11/1/KONV-2012-0027 projects. The work was carried out as part of the TÁMOP-4.2.2.D-15/1/KONV-2015-0017 project in the framework of the New Széchenyi Plan. The realisation of this project is supported by the European Union, and co-financed by the European Social Fund.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Appendices
Appendix A: estimation of model parameters for the binary Cu–Ni system
The integral molar excess Gibbs energy of the solid fcc Cu–Ni solution is written by the following equation [89, 90] (where x is the bulk mole fraction of Ni):
where L 0 (J/mol) and L 1 (J/mol) are the interaction energies between the components in the fcc Cu–Ni solid solution; the exponential term with \( \tau 1 = 3000 \;{\text{K}} \) ensures that the molar excess Gibbs energy of the solution tends to zero at high temperatures [91, 92], while the last term of Eq. (41) is due to magnetic ordering, where \( \beta_{m} \) (dimensionless) is the average magnetic moment per atom, \( \tau \equiv T/T_{\text{mo}} \), with \( T_{\text{mo}} \) (K) the critical temperature of magnetic ordering (the Curie temperature), \( f(\tau ) \) (dimensionless) is the following polynomial [93, 94]:
where p = 0.28 and D = 2.3425 for the fcc solid solution [93, 94]. The interaction energies of the fcc Cu–Ni solution are found in this paper using a method described in Appendix B. From the coordinates of the critical point of solid miscibility, x c = 0.673 and T c = 628 K [88]: L 0 = 10658.7 J/mol, L 1 = −3821.9 J/mol. The magnetic parameters are taken from [89] as
The partial molar excess Gibbs energies of the two components can be found from Eq. (41) using the following general thermodynamic equations [73, 74]:
The partial molar excess Gibbs energies of the components in the GB region are expressed by the same Eqs. (41)–(47), but x (the mole fraction of Ni in the bulk solid solution) should be replaced by x GB (the mole fraction of Ni in the GB region) and Eq. (41) should be multiplied by parameter \( \beta \) = 0.92, valid for fcc solid solutions (see above).
The high-angle GB energies of the two pure components are estimated using Eq. (33) and the data of [75, 76, 95] as
The molar volumes of the pure fcc metals Cu and Ni are quite close to each other; moreover, the lattice constant of the Cu–Ni solid solution changes linearly as a function of the mole fraction of Cu [96], and so the partial molar volumes will be taken equal to the molar volumes of the pure elements. That is why the simplified Eq. (37) applies: \( \omega_{i} \cong \omega_{i}^{o} \). The molar GB areas are calculated using Eq. (34) with f ≅ 1.24, valid for GBs of fcc crystals (see above). The molar volumes of pure components are taken from [97]. The final equations are as follows:
Appendix B: a method to find the parameters of Eq. (41) from the critical parameters of the miscibility gap
Let us consider a binary A–B solid or liquid solution with a miscibility gap, with the known measured coordinates of its maximum critical point: T c, K (=the absolute temperature of the critical point) and x c (=the mole fraction of component B in the critical point). Suppose by definition that the standard Gibbs energies of pure components equal zero. Then, the integral molar Gibbs energy of the solution in the two-parameter approximation of the Redlich–Kister polynomial is written as [91, 92]
where x (dimensionless) is the mole fraction of component B, L 0 (J/mol) and L 1 (J/mol) are the two interaction energies of the Redlich–Kister polynomial, valid at zero Kelvin; the exponential term is responsible for their temperature dependence, with \( \tau \) ≅ 3000 K [91, 92]. The condition of the critical point of the miscibility gap is that the second and third derivatives of Eq. (52) at T = T c and at x = x c will equal zero:
where L 0,Tc (J/mol) and L 1,Tc (J/mol) are the two interaction energies of the Redlich–Kister polynomial, valid at the critical temperature. The two parameters of Eqs. (53a) and (53b) can be expressed from these two equations as
If x c = 0.5, then L 1,Tc = 0 from Eq. (54a) and \( L_{{o,T{\text{c}}}} = 2RT_{\text{c}} \) from Eq. (54b), which is a well-known equation for the regular solution model. It should be mentioned that \( L_{o,Tc} \) has a positive solution only, if \( 0.211 < x_{c} < 0.789 \). As \( L_{o,Tc} \) should have a positive value for the thermodynamic properties to be consistent with the miscibility gap, Eqs. (54a) and (54b) can be used only within the interval of \( 0.3 < x_{c} < 0.7 \). If x c is out of this interval, then a more complex form of the Redlich–Kister polynomial Eq. (52) should be used.
The connection between the values of the interaction energies between zero Kelvin and the critical temperature is given using Eqs. (55a) and (55b) as
The method developed here can be applied to the Cu–Ni fcc solid solution, as x c = 0.673 [88], i.e. it is within the requested interval of \( 0.3 < x_{\text{c}} < 0.7 \). Substituting the data of x c = 0.673 and T c = 628 K [88] into Eqs. (54a), (54b), (55a) and (55b), the following results are obtained: L 0 = 10648 J/mol, L 1 = −3832 J/mol (at fixed \( \tau \) = 3000 K).
The heat of mixing of the alloy as a function of composition and temperature can be obtained from the above equations as [91]:
In Fig. 10, the experimental heat of mixing values measured at T = 1350 K [99] are compared with the results calculated by Eq. (56) and the parameters: L 0 = 10648 J/mol, L 1 = − 3832 J/mol, \( \tau \) = 3000 K, T = 1350 K. As the agreement is reasonably good, model Eq. (52) and the above model parameters describe both the thermodynamic properties and the phase diagram features reasonably well in the Cu–Ni system.
Appendix C: estimation of model parameters for the binary Fe–P bcc solution
Although the Fe–P system is very complex, only the bcc solid solution and the Fe3P stoichiometric compound will be considered here. As explained above (see “A second example of calculations: the Fe-P system” section), the A–B model system in this case will be A = Fe and B = Fe3P. That is why we need a relationship between the mole fraction of P in the real system and the mole fraction of Fe3P in the model system. In one mole of the Fe–P real solid solution, the number of moles of P atoms are x P (=the mole fraction of P in the binary Fe–P system). It is supposed here that the Gibbs energy change of the Fe3P complex formation from the elements Fe and P is so strong that more than 99 % of the P atoms within the bcc matrix are actually in the form of Fe3P complexes. Thus, the number of these molecules also equals x P (as each of these molecules contains one P atom). Then, the number of the remaining (free) Fe-atoms will be \( 1 - 4x_{\text{P}} \), as each Fe3P molecule contains four atoms. Therefore, the mole fraction of component B (Fe3P) in the model alloy is written as
The value of x P = 0.25 corresponds to the stoichiometry of the Fe3P compound. If this value is substituted into Eq. (57), \( x_{{{\text{Fe}}_{ 3} {\text{P}}}} = 1 \) is obtained, confirming that Eq. (57) obeys the reasonable boundary condition.
According to the phase diagram, the solid bcc Fe–P solution is in equilibrium with the stoichiometric compound Fe3P below 1321 K [88], with an eutectic point between these two phases at 1232 K. In the present calculation, the liquid Fe–P phase will be thermodynamically “suppressed” (neglected), and thus the bcc/Fe3P equilibrium will be extrapolated to the temperature of our interest, 1723 K. The thermodynamic properties of the phases in question are taken from [117] (all Gibbs energy values in J/mol-atom, temperature in K, \( x \equiv x_{\text{P}} \)):
with the following simplifying conditions:
Let me mention that below 1043 K Eqs. (59) and (63) also contain magnetic terms, but they are ignored here as our calculations are performed at 1723 K. The condition of formal thermodynamic equilibrium between the Fe–P solid solution and the stoichiometric compound Fe3P is
where \( x_{\text{P}}^{\text{sat}} \) is the saturation mole fraction of P in the bcc Fe–P solid solution, keeping equilibrium with phase Fe3P. If Eqs. (58)–(63) are substituted into Eq. (64), the resulting equation can be solved for \( x_{\text{P}}^{\text{sat}} \) at any given T. At T = 1321 K (the eutectic temperature) the result is \( x_{\text{P}}^{\text{sat}} = 0.0477 \). This corresponds to 2.7 w % of P, which is in good agreement with the measured value of 2.8 w % P [88]. This agreement validates the method described by Eqs. (58)–(64). For our temperature of interest T = 1723 K: \( x_{\text{P}}^{\text{sat}} = 0.0875 \). Substituting this value into Eq. (57): \( x_{{{\text{Fe}}_{ 3} {\text{P}}}}^{\text{sat}} = 0.1186 \).
Now, let us suppose that the Fe–Fe3P model system is described by the regular solution model. Then, the interaction energy within the framework of the regular solution model is written as
Substituting T = 1723 K and \( x_{{{\text{Fe}}_{ 3} {\text{P}}}}^{\text{sat}} = 0.1186 \) into Eq. (65), the value of the interaction energy in the model system Fe–Fe3P is found as \( {\Omega } = 37669 \) J/mol. One can see that this value is positive, i.e. the Fe and the Fe3P components repulse each other, and so they form a miscibility gap with the following critical temperature:
Substituting \( {\Omega } = 37699 \) J/mol into Eq. (66), \( T_{\text{c}} = 2265 \) K is found. Multiplying this value by \( \beta = 0.92 \), \( T_{\text{GBST,max}} = 2084 \) K is obtained from Eq. (39). As our T = 1723 K is below this maximum temperature, the formation of GBST is expected in the Fe–Fe3P model system at T = 1723 K. Therefore, the value of \( {\Omega } = 37669 \) J/mol will be used together with Eqs. (38a)–(38d) for modelling the excess Gibbs energies in the Fe–Fe3P model system.
The molar volume of bcc Fe crystal at 298 K is [118]: \( V_{{{\text{Fe,bcc,}}298\;{\text{K}}}}^{\text{o}} = 7.09\; \times \;10^{ - 6} \) m3/mol. Between T = 298 and 1723 K the bcc Fe crystal exhibits a linear expansion of about 2.4 % [119]. Then, the molar volume of bcc Fe at 1723 K: \( V_{{{\text{Fe,bcc,}}1723\;{\text{K}}}}^{o} = 7.61\; \times \;10^{ - 6} \) m3/mol. Substituting this value and \( f = 1.24 \) into Eq. (34): \( \omega_{{{\text{Fe,bcc,}}1723{\text{K}}}}^{\text{o}} = 4.05\; \times \;10^{4} \) m2/mol.
The molar volume of Fe3P crystal at 298 K is [96]: \( V_{{{\text{Fe}}_{ 3} {\text{P,298K}}}}^{\text{o}} = 2.87\; \times \;10^{ - 5} \) m3/mol. Its linear expansion is not known. Let us suppose that it is half that of the bcc Fe crystal, as compounds usually expand less than elements. Then: \( V_{{{\text{Fe}}_{ 3} {\text{P,1723}}}}^{\text{o}} = 2.97\; \times \;10^{ - 5} \) m3/mol. Substituting this value and \( f = 1.24 \) into Eq. (34): \( \omega_{{{\text{Fe}}_{ 3} {\text{P,1723}}\;{\text{K}}}}^{\text{o}} = 1.00\; \times \;10^{5} \) m2/mol.
The T dependence of the surface tension of pure liquid iron is written approximately as \( \sigma_{\text{Fe,l/g}}^{\text{o}} \cong 2.76 - 4.5\; \times \;10^{ - 4} \;T \) (J/m2) [75, 76]. Substituting this equation into Eq. (33), the interfacial high-angle GB energy of pure bcc iron is estimated as
Substituting T = 1723 K into Eq. (67): \( \sigma_{{{\text{Fe,bcc,1723}}\;{\text{K}}}}^{\text{o}} \cong 0.761 \) J/m2. The final task is to estimate the GB energy of a pure Fe3P compound. Due to the lack of a suitable theoretical equation, only the following relationship can be written: \( \omega_{{{\text{Fe}}_{ 3} {\text{P,1723}}\;{\text{K}}}}^{\text{o}} \cdot \sigma_{{{\text{Fe}}_{ 3} {\text{P,1723}}\;{\text{K}}}}^{\text{o}} \ll \omega_{{{\text{Fe,bcc,1723}}\;{\text{K}}}}^{\text{o}} \cdot \sigma_{{{\text{Fe,bcc,1723}}\;{\text{K}}}}^{\text{o}} \). Substituting the above values into this condition: \( \sigma_{\text{Fe3P,1723K}}^{\text{o}} \ll 0.308 \) J/m2. A more precise value is found semi-empirically in “A second example of calculations: the Fe-P system” section.
Rights and permissions
About this article
Cite this article
Kaptay, G. Modelling equilibrium grain boundary segregation, grain boundary energy and grain boundary segregation transition by the extended Butler equation. J Mater Sci 51, 1738–1755 (2016). https://doi.org/10.1007/s10853-015-9533-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-015-9533-8