Abstract
A 0.4C–2Si–1Cr–1Mo steel bar with an ultrafine-elongated grain (UFEG) structures was produced by multi-pass warm caliber rolling. The test sample was machined from the rolled bar with 0°, 45°, and 90° rotation along the rolling direction, and a static three-point bending test was conducted at ambient temperature. The toughness anisotropy on the steel with UFEG structures were studied, including the crack propagation on the basis of the microstructural features. The strength and toughness decreased with an increase in the rotation angle along the rolling direction. The toughness decreased drastically, compared to the strength. The notch orientation dependence on toughness is due to differences in the spatial distribution of weak sites such as {100} cleavage planes and boundaries of elongated grains. For the toughness design in ultrafine-grained materials, it is essential to understand the spatial distribution of these weak sites as well as the grain size.
Similar content being viewed by others

Introduction
Achieving strength and toughness in materials, that is, high strength in combination with resistance to fracture, is one of an eternal issue in the field of structural metallic materials. Since strengthening of materials reduces toughness [1–3], the idea for improving strength–toughness balance is always sought. It is reported that the refinement of crystal grains is an effective method for developing strength and toughness in metallic materials without the addition of alloying elements. However, compared with microstructure evolution through severe plastic deformation (SPD) and strengthening by grain refinement, there have been few studies on their toughness. The study of toughness is far more important in the development of ultrafine-grained (UFG) materials for structural and other applications.
Although a reduction in the grain size leads to higher strength on the basis of the Hall–Petch relation, it does not always lead to the improvement of toughness. In recent grain refinement studies, Hohenwarter et al. [4] showed that the ductile-to-brittle transition temperature, DBTT, was higher for submicrocrystalline grain sizes than for microcrystalline microstructures through a compact tension test for UFG armco iron processed by high-pressure torsion (HPT) and subsequent heat treatments. Furthermore, they showed that the fracture toughness depends strongly on crack orientations machined from the HPT disk. Toker et al. [5] indicated the significant effect of anisotropy on the impact toughness of UFG niobium–zirconium alloys processed by equal-channel angular extrusion. We [3, 6, 7] developed stronger, tougher steel, i.e., fail-safe steel, by a microstructural design based on heterogeneity that was lacking in the traditional concept. In fail-safe steel, the strengthening is attributed to ultrafine-elongated grains with nanometer-sized carbides, and the toughening is attributed to extrinsic fracture mechanisms of the crack-arrester type [3, 8–10], in which the propagation of a main crack associated with the heterogeneous microstructure with a strong α-fiber (RD∥〈101〉) texture is arrested. Namely, the property of toughness is sensitive to not only the size of crystal grains but also their orientation and shape because the fracture behavior is different by these microstructural parameters [2–7, 10, 11]. The fail-safe steel might also have an orientation dependence on the toughness because the microstructure consists of elongated grains and the spatial distribution of the {100} plane, which is a cleavage plane in bcc iron, changes. It is of interest to systematically study the effect of crack orientations on the toughness of fail-safe steel with ultrafine-elongated grain (UFEG) structures.
In the present study, a 0.4C–2Si–1Cr–1Mo steel bar with a UFEG structure was produced by multi-pass warm caliber rolling (WCR). The test sample was machined from the rolled bar with 0°, 45°, and 90° rotation along the rolling direction, and a static three-point bending test was conducted at ambient temperature. The effect of the initial notch orientation on toughness was studied, including the crack propagation on the basis of the microstructural features in the rolled bars. The anisotropic properties in the fail-safe steel were thus clarified.
Experimental
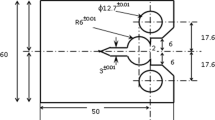
A low-alloy steel with a chemical composition of 0.39 C, 2.01 Si, 1.02 Cr, 1.0 Mo, 0.21 Mn, <0.001 P, <0.001 S, 0.004 Al, 0.0022 N, 0.001 O, and the balance Fe (all in mass%) was used in this study. A 100 kg ingot was prepared by vacuum induction melting and casting, homogenized at 1473 K, and then hot rolled to a 40-mm thickness plate. A block, 40-mm2 and 120-mm long, was cut out of the plate, solution treated at 1473 K for 3600 s to reduce undissolved carbide particles and then hot rolled into a bar of about 31-mm square, followed by water quenching to obtain the martensitic structure. The quenched bar was soaked at 773 K for 1 h, immediately subjected to a caliber rolling simulator [12] of the square/square type without any lubricant, and then air-cooled. Note that the sample was held for 0.3 ks in a furnace after three passes during the rolling and passed through twice for the final groove to control the cross-sectional shape of the bar. Eventually, a 14.3 × 14.3 × 930 mm3 rolled bar was produced. Hereafter, this sample is designated as the TF sample. To obtain quenched and tempered samples with the same tensile strength for comparison, a normalized bar was solution treated at 1223 K for 0.5 h, followed by oil quenching. Next, the bar was tempered at 773 K for 1 h and then water cooled. Hereafter, this sample is designated as the QT sample. The principal axes of the rolled bar in this study are defined as shown in Fig. 1a. The axis corresponding to the rolling direction is defined as the RD; that corresponding to the direction of the main working force at the final pass is ND; and that which is normal to the RD is defined as TD1 and TD2.
The appearance of specimens after the three-point bending test was observed through a digital camera, and fracture surfaces on the specimens were observed through a scanning electron microscope (SEM) operated at 15 kV. The microstructures in the central parts of the cross sections in the rolled bars were observed by the electron back-scattered diffraction (EBSD) method in an SEM equipped with a field emission gun.
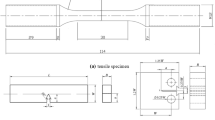
To clarify the notch orientation effect on the toughness, specimens used in a three-point bending test were taken from the rolled bar with 0°, 45°, and 90° rotation along the RD, and then both ends of the samples were bonded to a low-carbon steel, SM490, through electronic beam welding (EBW). Rectangular bars of 10 × 10 × 55 mm3 were machined for all specimens, and then a notch with a depth of a 0 = 5 mm and a root radius of ρ = 0.13 mm was introduced by electro-discharge machining with fine wire 0.1 mm in diameter. A notch tip in all test specimens was positioned at the center of the RD plane. The relation between the RD and the loading direction (LD) in each test sample is illustrated in Fig. 1b. The crack orientation in the TF(0°) sample is normal to the RD that in the TF(45°) sample has an angle of ~45° to the RD, and that in the TF(90°) sample is parallel to the RD. The shape and dimensions of three-point bending test and OM image near the notch root of the test specimen are illustrated in Fig. 2. The three-point bending test with a support distance of 40 mm at a cross-head speed of 0.05 mm min−1 was conducted at ambient temperature. The load–displacement response was recorded at a time step of 0.05 s. Nonlinear fracture mechanics methods based on ASTM Standard E1820-01 [13] were used to evaluate the fracture toughness. The apparent fracture energy, J, was calculated by the following formula:
where A pl is the area under the load P–displacement u curve, B is the specimen thickness, b is the ligament length (W−a 0), and u F denotes the displacement at which the test was terminated. All the values presented represent an average of two or three measurements.
Small plate samples with parallel length of 4 mm, a width of 3 mm, and a thickness of 1 mm were also machined from the bars with 0°, 45°, and 90° rotation along the RD and used for tensile testing at ambient temperature at a cross-head speed of 0.11 mm/min to investigate the strength anisotropy of the TF sample. Details of the configuration of small samples were given earlier [14].
Results and discussion
The static mechanical properties, including fracture toughness, J, are summarized in Table 1. In the TF(0°) sample, the tensile properties of the small plate specimens were similar to the results [3] of the JIS 14A specimens with a round cross section of 6 mm and a gage length of 30 mm. As expected, the TF samples exhibited an anisotropic tensile behavior due to the unique hierarchical anisotropic nanostructures, in contrast to the QT sample with an isotropic microstructure [14]. The yield strength, σys, decreased with an increase in the rotation angle along the RD. The σys of the TF(90°) sample was about 16 % lower than that of the TF(0°) sample. Similarly, the J also decreased with the rotation angle along the RD, but these J decreased drastically, compared to the strength. Although the J of the TF(45°) sample was somewhat higher than that of the QT sample, the TF(90°) sample exhibited the lowest toughness of 44 kJ/m2 among the present four samples despite the lowest tensile strength of 1.67 GPa, and the toughness was about 99 % lower than that of the TF(0°) sample which caused delamination by crack branching.
Figure 3a presents the bending load P–displacement u curves for the TF(45°) and TF(90°) samples and, for comparison, the curves [3] for the TF(0°) and the QT samples. Figure 3b–d show the appearances of the TF samples after the test, and Fig. 3e the SEM micrograph of fracture surface in the TF(90°) sample. The TF(90°) sample catastrophically fractured with a peak loading, P max, of 6.9 kN, such as the QT sample with P max = 12.3 kN. It thus showed typical brittle fracture behavior, and the cracks propagated directly across the center part of the test bar (Fig. 3d). On the other hand, in the TF(45°) sample, the first load drop occurred at loading, which was smaller than the P max of the QT sample and larger than the P max of the TF(90°) sample, and then a couple of load drops appeared. Eventually, the sample fractured into two pieces. The fracture path that was composed of cracks with an angle of ~ 45° to the LD (crack∠45°LD) and parallel to the LD (crack∥LD) was observable, as shown in Fig. 3c. Namely, the TF(45°) sample did not show a typical catastrophic fracture as the TF(90°) and QT samples did.
Figure 4 shows the image-quality map obtained by the EBSD analysis on the cross section of the plane along the RD for the TF sample and the inverse pole figures for the RD and TD2. Here, the {100} 〈110〉 texture and {110} 〈110〉 texture that cause delamination by crack branching in the TF(0°) sample [6, 10, 15] are highlighted in EBSD map, and the LD for each sample is illustrated. The insets in Fig. 4 show that the {100} 〈110〉 texture has a cleavage plane parallel to the RD and the {110} 〈110〉 texture has a cleavage plane with an angle of ±45º to the RD. The fraction of {100} 〈110〉 texture and {110} 〈110〉 texture was 20 and 34 %, respectively, under a tolerance angle of 15°. Although the fraction of the {100} 〈110〉 texture is smaller than that of the {110} 〈110〉 texture, grain boundaries parallel to a cleavage plane of the elongated {100} 〈110〉 grains are existent. A smaller grain microstructure provides a higher density of grain boundaries. In the TF sample, the transverse size of the elongated ferrite grains was 310 nm [3]. Hence, a crack related to a brittle fracture may preferentially propagate at these weak sites that are aligned in the RD.
The coherence length on the {100} cleavage plane parallel to the RD in the {100} 〈110〉 grains is longer than that in the {110} 〈110〉 grains because of the elongated grains. A brittle fracture occurs when the effective yield stress in the process zone at the notch tip exceeds the cleavage fracture stress (transgranular brittle fracture stress) or the grain-boundary fracture stress (intergranular brittle fracture stress). These fracture stresses increase with a reduction in the average grain size, and this grain-size dependence is higher than the grain-size dependence of a yield stress [16]. According to the Griffith equation, the brittle fracture stress, σF, related to these weak sites is a function of the cohesive energy of fracture, γ (in this case, the cohesive energy along the cleavage plane and the grain-boundary cohesive energy), and the crack size (in this case, it is replaced by the effective grain size, d eff) [16–18]. These have a relation of \( \sigma_{\text{F}} \propto \gamma^{{\left( { 1/ 2} \right)}} \times d_{\text{eff}}^{( - 1/ 2)} \); i.e., σF becomes larger with decreasing d eff. For the TF sample with the UFEG structure, the brittle fracture stresses in each direction illustrated in Fig. 5b–d are expressed by a relation of σF⊥RD ≪ σF∠45°RD < σF∥RD. If the Tresca yield criterion is assumed in the process zone within the plastically yielding region of the notch tip, the triaxial tension stress in the plane strain condition is represented by the following:
As a result, the yield stress of the notched specimen is greater than the uniaxial yield stress, σys, shown in Table 1. The maximum value of each stress component found at the elastic–plastic interface in the process zone is expressed by σ xx(max) ≈ 1.6σys, σ yy(max) ≈ 2.6σys, and σ zz(max) ≈ 2.1σys [17, 19] although these exact values have to be calculated through numerical simulations because the stresses depend on the geometry of the notch tip, ligament length, specimen thickness, and anisotropic properties. In addition, the stresses in the process zone have the distribution shown in Fig. 5a [20]. Here, the axis parallel to the LD is defined as x and the one normal to the LD is y. In general, a crack propagates parallel to the LD because the tensile stress, σ yy , vertical to the LD occurs by a bending load. In the TF(0°) sample shown in Fig. 3b, the crack did not propagate parallel to the LD because a cleavage plane was almost nonexistent along the LD under the structures with α-fiber texture. A delaminating crack related to a brittle fracture induced by σ xx > σF⊥RD occurred before a ductile fracture (Fig. 5b). This phenomenon appeared as the first drop P 1 and a subsequent load increase (Fig. 3a). Namely, the boundaries of elongated grains lying normal to the initial crack orientation and the {100} cleavage planes constituted a barrier against crack propagation along the LD. Eventually, its J increased remarkably due to this crack branching. In contrast, in the TF(90°) sample, the tensile direction of the stress, σ yy , induced by a bending load corresponds to the direction of the lowest brittle fracture stress, σF⊥RD (Fig. 5d); therefore, the fracture was dominated by crack path parallel to the LD, as shown in Fig. 3d. At this time, in the fracture surface, microscopically, not only a cleavage plane related to {110} 〈110〉 grains but also a fracture plane (fine dimple) associated with a plastic deformation was observable, together with crack∥LD. This fracture surface characterized by a quasi-cleavage shown in Fig. 3e was very similar to the delaminating structure observed in the TF(0°) sample [3, 14, 15]. Eventually, the peak-bending load exhibited the lowest value and the J decreased remarkably because a barrier lying normal to crack propagation is nonexistent. In the TF(45°) sample, the cleavage plane of the {110} 〈110〉 grains is existent along the LD, as shown in Fig. 5c. However, the crack first propagated along an angle of ±45° to the LD due to σF⊥RD ≪ σF∠45°RD and \( \sqrt {\sigma_{xx}^{2} + \sigma_{yy}^{2} } > \sigma_{yy} > \sigma_{xx} \). Subsequently, a zigzag fracture path composed of crack∥LD and crack∠45°LD, macroscopically, appeared, as shown in Fig. 3c. That is, weak planes related to {100} 〈110〉 grains and the boundaries of elongated grains as well as a cleavage plane parallel to LD related to {110} 〈110〉 grains were induced during the bending test. Hence, the P–u curves did not show typical brittle fracture behavior, and the J was larger than that of the TF(90°) sample due to the deflection of the crack path.
Conclusions
In conclusion, the present results demonstrated anisotropic properties in a 0.4C–2Si–1Cr–1Mo steel with ultrafine-elongated grain structure. The strength and the toughness decreased with an increase in rotation angle along the rolling direction, especially, the toughness decreased remarkably compared to the strength. The notch orientation dependence on toughness is due to differences in the spatial distribution of weak sites, such as {100} cleavage planes and boundaries of elongated grains. For the toughness design of fail-safe steel, it is essential to understand the spatial distribution of these weak sites as well as the grain size.
References
Lu K (2010) Science 328:319
Launey ME, Ritchie RO (2009) Adv Mater 21:2103
Inoue T, Kimura Y, Ochiai S (2012) Sci Technol Adv Mater 13:035005
Hohenwarter A, Kammerhofer C, Pippan R (2010) J Mater Sci 45(17):4805. doi:10.1007/s10853-010-4635-9
Toker SM, Rubitschek F, Niendorf T, Canadinc C, Maier HJ (2012) Scripta Mater 66:435
Kimura Y, Inoue T, Yin F, Tsuzaki K (2008) Science 320(5879):1057
Nie Y, Kimura Y, Inoue T, Yin F, Akiyama E, Tsuzaki K (2012) Metall Mater Trans 43A:1670
Embury JD, Petch NJ, Wraith AE, Wright ES (1967) Trans Metall Soc AIME 239:114
She J, Inoue K, Ueno K (2000) J. Mater Sci Lett 19:45
Bourell DL (1983) Metall Trans A 14:2487
Rao KTV, Ritchie RO (1989) Mater Sci Technol 5:882
Inoue T, Yin F, Kimura Y (2007) Mater Sci Eng 66A:114
ASTM E1820-01 (2005) Standard test method for measurement of fracture toughness. ASTM International, West Conshohocken, pp 1036–1081
Kimura Y, Inoue T, Yin F, Tsuzaki K (2010) ISIJ Int 50:152
Inoue T, Yin F, Kimura Y, Tsuzaki K, Ochiai S (2010) Metall Mater Trans 40A:341
Gilbert A, Hahn GT, Reid CN, Wilcox BA (1964) Acta Mater 12:754
Ma H (1998) Int J Fract 89:143
Kameda J, Nishiyama Y (2011) Mater Sci Eng 528A:3705
Matsuda S, Kawashima Y, Sekiguchi S, Okamoto M (1982) Tetsu-to-Hagane 68:435 (in Japanese)
Dieter GE (1988) Mechanical metallurgy SI metric edition. McGraw-Hill Book Co, Singapore, pp 265–268
Acknowledgement
We thank S. Kuroda, Y. Taniuchi, and K. Nakazato for materials processing, T. Kanno and G. Aragane for sample preparation of three-point bending test including welding, Ms. E. Motoki for her experimental assistance in the microstructural observations, and Ms. Y. Yano for her illustration used in this paper. This study was partly supported by the grants from the JFE 21st Century Foundation, and KAKENHI B (No. 23360312). These grants are gratefully appreciated.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Inoue, T., Kimura, Y. Effect of initial notch orientation on fracture toughness in fail-safe steel. J Mater Sci 48, 4766–4772 (2013). https://doi.org/10.1007/s10853-012-6874-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-012-6874-4