Assigning physical significance to the diffuse interface between terraces in phase-field modeling of steps on crystal surfaces: modeling step–step interaction

Abstract

We apply a modified phase-field modeling approach to the analysis of steps on a crystalline surface. Specifically, we are interested in capturing phenomena associated with the interaction between steps. To this end, we assign a physical significance to the form of the interfacial region between terraces (i.e. steps), inherent in the phase field approach, by tuning the multi-well potential to produce long-range interaction energies varying as 1/l², where l is half the distance between steps. Resultant repulsive interactions between adjacent steps of the same sign are shown to affect step-flow kinetics in a manner consistent with curvature-driven interfacial relaxation. This phenomenon is further demonstrated to cause dislocation-driven (spiral) crystal growth kinetics to deviate, for large supersaturation and Burgers vector values, from the classical quadratic growth law. Attractive interactions between adjacent steps of opposite sign, also resulting from the finite interfacial width, are briefly explored particularly with respect to their possible impact on two-dimensional nucleation.

Appendices

Appendix 1: derivation of step–step interaction parameters

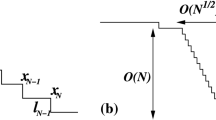
In this appendix we provide details of the analytical treatment leading to the derivation of Eqs. 17–23. We first start with the derivation of the case of repulsing steps in a step train, consistent with Fig. 1a and described by the stationary 1-D solution of Eq. 7 in the spatial interval [−l, l] with boundary conditions given by Eq. 14. Our goal is to demonstrate how our choice of g(ϕ), given by Eq. 13, leads to the desired power law dependence of step–step interaction energy on the distance between steps. Moreover, we wish to find the relation between the parameters of the interaction law and those appearing in Eqs. 7 (τ, ξ, W, λ) and 13 (α).

The stationary 1-D version of Eq. 7, with the assumption of relatively low supersaturation values (λσ ≪ W and λσ ≪ ξ²) is given by:

$$ \xi^2\frac{{\hbox{d}}^2\phi}{{\hbox{d}}x^2} - Wg^{\prime}(\phi)=0.$$

(30)

This equation can be re-written and integrated according to:

$$ \xi^2\int\frac{{\hbox{d}}\phi}{{\hbox{d}}x}d\left(\frac{{\hbox{d}}\phi}{{\hbox{d}}x}\right)= W\int {\hbox{d}}g(\phi),$$

(31)

which, while remembering that g(ϕ(l)) = 0, yields:

$$ \frac{\xi^2}{2}\left(\frac{{\hbox{d}}\phi}{{\hbox{d}}x}\right)^2 = Wg(\phi)+\frac{\xi^2}{2}G_r,$$

(32)

where $G_r\equiv\left(\frac{{\hbox{d}}\phi}{{\hbox{d}}x}|_{x=l}\right)^2.$

Taking the square root of both sides of Eq. 32, while remembering that in this case $\frac{{\hbox{d}}\phi}{{\hbox{d}}x}<0,$ rearranging the results and integrating between x = 0 (ϕ = 1/2) and x = l (ϕ = 0) yields:

$$ \begin{aligned} l =\,& \xi \int\limits_{0}^{1/2} \frac{{\hbox{d}}\phi}{\sqrt{2Wg(\phi)+\xi^2G_r}}\\ =\,& \xi \int\limits_{0}^{\infty} \frac{{\hbox{d}}\phi}{\sqrt{2W{\tilde{g}}(\phi)+\xi^2G_r}}- \xi \int\limits_{1/2}^{\infty} \frac{{\hbox{d}}\phi}{\sqrt{2W{\tilde{g}}(\phi)+\xi^2G_r}},\end{aligned}$$

(33)

where ${\tilde{g}}(\phi)\equiv \phi^{\alpha}.$ Assuming a relatively large distance between steps ($G_r \ll 2W/(2^{\alpha}\xi^2)$) we now obtain:

$$ \begin{aligned} l =\,&\xi \int\limits_{0}^{\infty} \frac{{\hbox{d}}\phi}{\sqrt{2W\phi^{\alpha}+\xi^2G_r}}- \xi \int\limits_{1/2}^{\infty}\frac{{\hbox{d}}\phi}{\sqrt{2W\phi^{\alpha}}}\\ =\,&\frac{q_r}{\sqrt{G_r}}\left(\frac{\xi^2G_r}{2W} \right)^{1/\alpha}-\frac{2^{\frac{\alpha-1}{2}}}{\alpha-2}\frac{\xi}{\sqrt{W}},\end{aligned} $$

(34)

where q_r is defined in Eq. 20.

The step energy is now calculated using the equation:

$$ \gamma_{\rm st} = \int\limits_{-l}^l \left[\frac{\xi^2}{2} \left(\frac{{\hbox{d}}\phi}{{\hbox{d}}x}\right)^2 + W g(\phi)\right] {\hbox{d}}x.$$

(35)

This equation is next re-written, with the help of Eq. 32 while remembering that $\frac{{\hbox{d}}\phi}{{\hbox{d}}x}<0,$ to yield:

$$ \begin{aligned} \gamma_{\rm st} =& \int\limits_{-l}^l \left[\xi^2 \left(\frac{{\hbox{d}}\phi}{{\hbox{d}}x}\right)^2 - \frac{\xi^2}{2}G_r\right] {\hbox{d}}x\\ =& \xi\int\limits_{l}^{-l} \sqrt{2Wg(\phi)+\xi^2G_r}\frac{{\hbox{d}}\phi}{{\hbox{d}}x}{\hbox{d}}x - \xi^2 G_r l\\ =& \xi\int\limits_{0}^1\sqrt{2Wg(\phi)+\xi^2G_r}{\hbox{d}}\phi - \xi^2 G_r l.\end{aligned}$$

(36)

We next compare the first term of this result with Eq. 33, while accounting for symmetry with respect to ϕ = 0.5 and remembering our assumption of a relatively large distance between steps. It can be seen this term is proportional to the integral of Eq. 33 with respect to G_r. With this information, together with Eq. 34, we can see that:

$$ \begin{aligned} \gamma_{\rm st} =& 2\xi\int\limits_{0}^{1/2} \sqrt{2Wg(\phi)+\xi^2G_r}{\hbox{d}}\phi - \xi^2 G_r l\\=& \xi^2\int\limits_{0}^{G_r} l(G^*_r){\text{d}}G^*_r - \xi^2 G_r l+\gamma_{{\rm st}_0}\\ =& \xi^2\int\limits_{0}^{G_r} \frac{q_r}{\sqrt{G^*_r}}\left(\frac{\xi^2G^*_r}{2W} \right)^{1/\alpha}{\hbox{d}}G^*_r- \frac{2^{\frac{\alpha-1}{2}}}{\alpha-2}\frac{\xi^3} {\sqrt{W}}G_r\\ &- \xi^2 G_r l+\gamma_{{\rm st}_0},\end{aligned} $$

(37)

where $\gamma_{{\rm st}_0}$ is the constant of integration (with respect to G_r) which corresponds to the value of the step energy in the limit of l→∞ (G_r→0) in which case step–step interactions disappear. Equation 37 is further simplified (with the aid of Eq. 34 to yield:

$$ \begin{aligned} \gamma_{\rm st}=& \frac{2\alpha}{2+\alpha}\xi^2G_r\left(l+\frac{2^{\frac{\alpha-1}{2}}} {\alpha-2}\frac{\xi}{\sqrt{W}}\right)-\frac{2^{\frac{\alpha-1} {2}}} {\alpha-2}\frac{\xi^3}{\sqrt{W}}G_r\\ &- \xi^2 G_r l+\gamma_{{\rm st}_0}.\end{aligned} $$

(38)

Remembering (see Eq. 16) that $\gamma_{\rm int} = \gamma_{\rm st} - \gamma_{{\rm st}_0}$ and inserting the dependence of G_r on l (extracted from Eq. 34) into Eq. 38 yields the following expression for the step–step interaction energy:

$$ \begin{aligned} \gamma_{\rm int} =& \left(\frac{\alpha-2} {\alpha+2}\right)\xi^2\left(l+\frac{2^{\frac{\alpha-1}{2}}} {\alpha-2}\frac{\xi}{\sqrt{W}}\right)G_r\\ =& \left(\frac{\alpha-2}{\alpha+2}\right)\left[\frac{2W}{(\xi q_r)^{\alpha}}\right]^{\frac{2}{2-\alpha}}\left(l+\frac{2^{\frac{\alpha-1}{2}}} {\alpha-2}\frac{\xi}{\sqrt{W}}\right)^{\frac{2+\alpha}{2-\alpha}}\\ =& b_r\left(l+\frac{2^{\frac{\alpha-1}{2}}} {\alpha-2}\frac{\xi}{\sqrt{W}}\right)^{\frac{2+\alpha}{2-\alpha}},\end{aligned} $$

(39)

where b_r is given by Eq. 18. Remembering the above assumption of relatively large distance between steps $(G_r \ll 2W/(2^{\alpha}\xi^2)),$ we can see that for $l\gg\frac{2^{\frac{\alpha-1}{2}}}{\alpha-2}\frac{\xi} {\sqrt{W}}$ we obtain, from Eq. 39, the power law given by Eq. 17.

We next return to Eq. 33 and consider now the case of short distances between steps $(G_r \gg 2W/(2^{\alpha}\xi^2)).$ With this assumption it is easy to show that

$$ l=(4G_r)^{-1/2},$$

(40)

and following Eq. 36 one can show (with the above short step–step distance assumption) that:

$$ \gamma_{\rm st} = \xi^2\left(\sqrt{G_r}-G_rl\right),$$

(41)

and, after inserting G_r(l) from Eq. 40 into Eq. 41 we obtain:

$$ \gamma_{\rm st} = \xi^2\left[1/(2l)-l/(4l^2)\right]=0.25\xi^2/l.$$

(42)

Now $G_r \gg 2W/(2^{\alpha}\xi^2) \geq 2Wg(\phi)/\xi^2$ (for all values of ϕ), and as a result $\xi^2\sqrt{G_r} \gg \xi\sqrt{2Wg(\phi)}$ (for all values of ϕ). Therefore, $\int_0^{1/2}\xi^2\sqrt{G_r}{\hbox{d}}\phi\gg\int_0^{1/2}\xi\sqrt{2Wg(\phi)}{\hbox{d}}\phi$ and, due to symmetry with respect to ϕ = 0.5, $\xi^2\sqrt{G_r}\gg\left(\sqrt{2}\int_0^{1}\sqrt{g(\phi)}{\hbox{d}}\phi\right)\xi\sqrt{W}.$ Comparing with Eqs. 10 and 11, we see that we have obtained $\xi^2\sqrt{G_r}\gg\gamma_{{\rm st}_0}.$ Using G_r(l) from Eq. 40 we further understand that ξ²/(2l) ≫ $\gamma_{{\rm st}_0}$ and, with the aid of Eq. 42, it is reasonable to conclude that γ_st ≫ $\gamma_{{\rm st}_0}$ which means that the step energy is dominated by step–step interactions and Eq. 42 is equivalent to Eq. 23.

Finally, we address the case of attracting steps, consistent with Fig. 1b and described by the stationary 1-D solution of Eq. 7 in the spatial interval [ − l,l] with boundary conditions given by Eq. 15. Our starting point is Eq. 30 which, when remembering $\frac{{\hbox{d}}\phi}{{\hbox{d}}x}|_{x=l}=0$ yields:

$$ \frac{\xi^2}{2}\left(\frac{{\hbox{d}}\phi}{{\hbox{d}}x}\right)^2 = Wg(\phi)-WG_a,$$

(43)

where G_a≡g(ϕ(x))|_x=l. Following the same approach used in the derivation of Eqs. 33 and 34 we next isolate l under the assumption that $G_a\ll\frac{1}{2^{\alpha}}$ while understanding that $\frac{{\hbox{d}}\phi}{{\hbox{d}}x}<0,$ x = 0 corresponds to ϕ = 1/2 and x = l corresponds to ϕ(l) = G ^1/α _a . The result is given by:

$$ \begin{aligned} l =&\xi \int\limits_{G_a^{1/\alpha}}^{1/2} \frac{{\hbox{d}}\phi}{\sqrt{2W(\phi^{\alpha}-G_a)}}\\ =& \xi\int\limits_{G_a^{1/\alpha}}^{\infty} \frac{{\hbox{d}}\phi}{\sqrt{2W(\phi^{\alpha}-G_a)}}- \xi \int\limits_{1/2}^{\infty}\frac{{\hbox{d}}\phi}{\sqrt{2W\phi^{\alpha}}}\\ =&\frac{\xi q_a}{\sqrt{2W}}G_a^{\frac{2-\alpha}{2\alpha}}- \frac{2^{\frac{\alpha-1} {2}}} {\alpha-2}\frac{\xi}{\sqrt{W}},\\ \end{aligned} $$

(44)

where q_a is defined in Eq. 21.

We next start with the definition of the step energy given by Eq. 35 and following the same logic as in the case of step–step repulsion, with the aid of Eq. 43, we can show that:

$$ \begin{aligned} \gamma_{\rm st} =& \int\limits_{-l}^l \left[\xi^2 \left(\frac{{\hbox{d}}\phi}{{\hbox{d}}x}\right)^2 + WG_a\right] {\hbox{d}}x\\ =& \xi\int\limits_{l}^{-l} \sqrt{2W \left[g(\phi)-G_a \right]}\frac{{\hbox{d}}\phi}{{\hbox{d}}x}{\hbox{d}}x + 2WG_al\\ =& 2\xi\int\limits_{G_a^{1/\alpha}}^{1/2} \sqrt{2W\left[g(\phi)-G_a\right]}{{\hbox{d}}\phi}+ 2WG_al,\end{aligned} $$

(45)

which is further simplified to become:

$$ \begin{aligned} \gamma_{\rm st} =& -2W\int\limits_{0}^{G_a} l(G^*_a){\hbox{d}}G^*_a +2W G_a l+\gamma_{{\rm st}_0}\\ =& -2W\int\limits_{0}^{G_a} \frac{\xi q_a}{\sqrt{2W}}{G^*_a}^{\frac{2-\alpha} {2\alpha}}{\hbox{d}}G^*_a+ \frac{2^{\frac{\alpha+1} {2}}}{\alpha-2}{\xi}{\sqrt{W}}G_a\\ &+ 2WG_al+\gamma_{{\rm st}_0}\\ =&-\frac{2\alpha}{2+\alpha}\xi q_a\sqrt{2W}G_a^{\frac{2+\alpha} {2\alpha}}+ \frac{2^{\frac{\alpha+1}{2}}}{\alpha-2}{\xi}{\sqrt{W}}G_a \\ &+ 2WG_al+\gamma_{{\rm st}_0}.\end{aligned} $$

(46)

Inserting G_a(l) from Eq. 44 and recalling Eq. 16, we obtain the interaction energy:

$$ \begin{aligned} \gamma_{\rm int} =& \left(\frac{2-\alpha}{\alpha+2}\right)\left[\frac{2W}{(\xi q_a)^{\alpha}}\right]^{\frac{2}{2-\alpha}}\left(l+\frac{2^{\frac{\alpha-1}{2}}} {\alpha-2}\frac{\xi}{\sqrt{W}}\right)^{\frac{2+\alpha}{2-\alpha}}\\ =& b_a\left(l+\frac{2^{\frac{\alpha-1}{2}}} {\alpha-2}\frac{\xi}{\sqrt{W}}\right)^{\frac{2+\alpha}{2-\alpha}},\end{aligned}$$

(47)

where b_a is given by Eq. 19. Here, as in the case of repulsion, the assumption of large step–step distances $(G_a\ll\frac{1}{2^{\alpha}}, l\gg\frac{2^{\frac{\alpha-1}{2}}} {\alpha-2}\frac{\xi}{\sqrt{W}})$ renders Eq. 47 equivalent to the power law given by Eq. 17.

Appendix 2: testing alternative forms of g(ϕ) and p(ϕ)

In the text we discuss the replacement of Eq. 13, for ψ_c < ψ(ϕ) < 1 − ψ_c, by a simple constant valued interpolating function yielding g(ϕ) given by Eq. 26. In addition to varying the value of ψ_c (mentioned in the text), we tested the sensitivity of the model to this interpolating function using a more general alternative to Eq. 26 given by:

$$ g(\phi)=\left\{\begin{array}{llllll} \psi(\phi)^{6}, &\qquad \psi(\phi) \le \psi_c \\ \Sigma_{i=0}^{m}c_i\psi(\phi)^i\left[1-\psi(\phi)\right]^i, & \psi_c < \psi(\phi) < 1-\psi_c \\ \left[1-\psi(\phi)\right]^{6},&\,\qquad\psi(\phi) \ge 1-\psi_c\end{array}\right.,$$

(48)

with c_i determined by enforcing continuity in g(ϕ) and its derivatives (up to order m) at ψ_c and 1 − ψ_c. For a given level of supersaturation, and physical parameter values, results with m = 0 (in which case Eq. 48 is equivalent to Eq. 26) were found to be virtually the same as those achieved with m = 3.

Results presented in Figs. 3 and 4 were reproduced using three alternative forms for p(ϕ), all of which are monotonically increasing functions which return the value of the phase-field parameter on terraces (p(n) = n) and guarantee the existence of stable minima in f(ϕ) (given by Eqs. 4 and 13) at integer values of ϕ for any value of σ. In the first case, Eq. 24 (with α = 6) was modified using a linear interpolation in the region ψ_c < ψ(ϕ) < 1 − ψ_c, yielding:

$$ p(\phi)=\left\{ \begin{array}{llllll}0.5\left[\frac{\psi(\phi)} {0.5}\right]^{7}+n(\phi), &\qquad \psi(\phi) \le \psi_c\\ 0.5\left(\frac{\psi_c} {0.5}\right)^{7}+\,n(\phi)+\,\frac{\left[\psi(\phi)-\psi_c\right]} {2\left(1-2\psi_c\right)}& \\ \times \left[2-\left(\frac{1-\psi_c} {0.5}\right)^{7}-\,\left(\frac{\psi_c} {0.5}\right)^{7}\right], & \psi_c <\psi(\phi) < 1-\psi_c\\ 1-0.5\left[\frac{1-\psi(\phi)} {0.5}\right]^{7}+\,n(\phi),&\,\qquad \psi(\phi) \ge 1-\psi_c \end{array}\\ \right..$$

(49)

The second case, given by:

$$ p(\phi)=\left\{\begin{array}{llllll} 0.25\left[\frac{\psi(\phi)} {0.5}\right]^{7}+\,n(\phi), &\qquad \psi(\phi) \le \psi_c \\ 0.25\left(\frac{\psi_c}{0.5}\right)^{7}+n(\phi)+\, \frac{\left[\psi(\phi)-\psi_c\right]} {4\left(1-2\psi_c\right)}&\\ \times \left[4-\left(\frac{1-\psi_c}{0.5}\right)^{7}-\,\left(\frac{\psi_c}{0.5}\right)^{7}\right], & \psi_c <\psi(\phi) < 1-\psi_c\\ 1-0.25\left[\frac{1-\psi(\phi)}{0.5}\right]^{7}+\,n(\phi),&\,\qquad \psi(\phi) \ge 1-\psi_c \end{array}\right., $$

(50)

is similar in form to Eq. 49 except for the fact that the power law terms are pre-multiplied by a factor of 0.25 rather than by a factor of 0.5. Note that in Eq. 24 the factor of 0.5 is necessary for continuity at ϕ = 0.5 (where p(0.5) = 0.5). Notice also that the specific forms of the linear part of p(ϕ) in Eqs. 49 and 50 (in the region ψ_c < ψ(ϕ)  < 1 − ψ_c) guarantees continuity of this function for all values of ϕ (where here too p(0.5) = 0.5).

The last alternative form of p(ϕ) is given by

$$ p(\phi)=\left\{\begin{array}{ll}0.5\left[\frac{\psi(\phi)} {0.5}\right]^{8}+\,n(\phi), & \psi(\phi)<1/2\\ 1-0.5\left[\frac{1-\psi(\phi)}{0.5}\right]^{8}+\,n(\phi),& \psi(\phi) \ge 1/2 \end{array}\\ \right.,$$

(51)

where in this case the exponent of the power law was increased. Repeating calculations for the cases involving a non-zero value of supersaturation (presented in Figs. 3 and 4), using all three alternative forms of p(ϕ) (Eqs. 49–51 with ψ_c = 0.35), yielded results virtually the same as those obtained using Eq. 24.