Skip to main content
SpringerLink
Log in

Statistical Model and ML-EM Algorithm for Emission Tomography with Known Movement

  • Published:
Journal of Mathematical Imaging and Vision Aims and scope Submit manuscript

Abstract

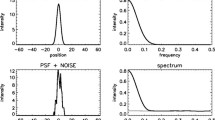
In positron emission tomography, movement leads to blurry reconstructions when not accounted for. Whether known a priori or estimated jointly to reconstruction, motion models are increasingly defined in continuum rather that in discrete, for example by means of diffeomorphisms. The present work provides both a statistical and functional analytic framework suitable for handling such models. It is based on time-space Poisson point processes as well as regarding images as measures, and allows to compute the maximum likelihood problem for line-of-response data with a known movement model. Solving the resulting optimisation problem, we derive an maximum likelihood expectation maximisation (ML-EM)-type algorithm which recovers the classical ML-EM algorithm as a particular case for a static phantom. The algorithm is proved to be monotone and convergent in the low-noise regime. Simulations confirm that it correctly removes the blur that would have occurred if movement were neglected.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Abadi, M., et al.: TensorFlow: Large-scale machine learning on heterogeneous systems. Software available from https://www.tensorflow.org/ (2015)

  2. Adler, J., Kohr, H., Öktem, O.: ODL-A Python Framework for Rapid Prototyping in Inverse Problems. Royal Institute of Technology, Stockholm (2017)

    Google Scholar 

  3. Blume, M., Martinez-Moller, A., Keil, A., Navab, N., Rafecas, M.: Joint reconstruction of image and motion in gated positron emission tomography. IEEE Trans. Med. Imaging 29(11), 1892–1906 (2010)

    Article  Google Scholar 

  4. Brezis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, Berlin (2010)

    Book  Google Scholar 

  5. Burger, M., Dirks, H., Schönlieb, C.-B.: A variational model for joint motion estimation and image reconstruction. SIAM J. Imaging Sci. 11(1), 94–128 (2018)

    Article  MathSciNet  Google Scholar 

  6. Chan, C., Onofrey, J., Jian, Y., Germino, M., Papademetris, X., Carson, R.E., Liu, C.: Non-rigid event-by-event continuous respiratory motion compensated list-mode reconstruction for PET. IEEE Trans. Med. Imaging 37(2), 504–515 (2018)

    Article  Google Scholar 

  7. Dalca, A.V., Guttag, J., Sabuncu, M.R.: Anatomical priors in convolutional networks for unsupervised biomedical segmentation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 9290–9299 (2018)

  8. Dawood, M., Jiang, X., Schäfers, K.P. (eds): Correction techniques in emission tomography. In: Series in Medical Physics and Biomedical Engineering. CRC Press (2008)

  9. Georgiou, T.T.: Solution of the general moment problem via a one-parameter imbedding. IEEE Trans. Autom. Control 50(6), 811–826 (2005)

    Article  MathSciNet  Google Scholar 

  10. Gigengack, F., Jiang, X., Dawood, M., Schäfers, K.P.: Motion Correction in Thoracic Positron Emission Tomography. Springer, Berlin (2015)

    Book  Google Scholar 

  11. Hinkle, J., Szegedi, M., Wang, B., Salter, B., Joshi, S.: 4D CT image reconstruction with diffeomorphic motion model. Med. Image Anal. 16(6), 1307–1316 (2012)

    Article  Google Scholar 

  12. Jacobson, M., Fessler, J.: Joint estimation of image and deformation parameters in motion-corrected PET. In: 2003 IEEE Nuclear Science Symposium. Conference Record (IEEE Cat. No.03CH37515) (-nil), p. nil

  13. Jacobson, M.W., Fessler, J.A.: Joint estimation of respiratory motion and activity in 4D PET using CT side information. In: 3rd IEEE International Symposium on Biomedical Imaging: Nano to Macro. Arlington, VA, April 6–9, pp. 275—278 (2006)

  14. Last, G., Penrose, M.: Lectures on the Poisson Process, vol. 7. Cambridge University Press, Cambridge (2017)

    Book  Google Scholar 

  15. Li, T., Zhang, M., Qi, W., Asma, E., Qi, J.: Motion correction of respiratory-gated PET image using deep learning based image registration framework. In: 15th International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine, vol. 11072, International Society for Optics and Photonics, p. 110720Q (2019)

  16. Mair, B., Rao, M., Anderson, J.: Positron emission tomography, Borel measures and weak convergence. Inverse Prob. 12(6), 965 (1996)

    Article  MathSciNet  Google Scholar 

  17. Öktem, O., Pouchol, C., Verdier, O.: Spatiotemporal PET reconstruction using ML-EM with learned diffeomorphic deformation. In: International Workshop on Machine Learning for Medical Image Reconstruction, pp. 151–162. Springer (2019)

  18. Posner, E.: Random coding strategies for minimum entropy. IEEE Trans. Inf. Theory 21(4), 388–391 (1975)

    Article  MathSciNet  Google Scholar 

  19. Pouchol, C., Verdier, O.: The ML-EM algorithm in continuum: sparse measure solutions. Inverse Prob. 36, 3 (2020)

    Article  MathSciNet  Google Scholar 

  20. Qiao, F., Pan, T., Clark, J.W., Mawlawi, O.R.: A motion-incorporated reconstruction method for gated PET studies. Phys. Med. Biol. 51(15), 3769–3783 (2006)

    Article  Google Scholar 

  21. Rahmim, A., Tang, J., Zaidi, H.: Four-dimensional image reconstruction strategies in cardiac-gated and respiratory-gated PET imaging. PET Clin. 8(1), 51–67 (2013)

    Article  Google Scholar 

  22. Reader, A.J., Verhaeghe, J.: 4D image reconstruction for emission tomography. Phys. Med. Biol. 59(22), R371–R418 (2014)

    Article  Google Scholar 

  23. Rudin, W.: Functional Analysis, International Series in Pure and Applied Mathematics, 2nd edn. McGraw-Hill Inc, New York (1991)

    Google Scholar 

  24. Shepp, L.A., Vardi, Y.: Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imaging 1(2), 113–122 (1982)

    Article  Google Scholar 

  25. Vardi, Y., Shepp, L., Kaufman, L.: A statistical model for positron emission tomography. J. Am. Stat. Assoc. 80(389), 8–20 (1985)

    Article  MathSciNet  Google Scholar 

  26. Younes, L.: Shapes and Diffeomorphisms, vol. 171 of Applied Mathematical Sciences. Springer, Berlin (2010)

Download references

Author information

Authors and Affiliations

  1. MAP5 Laboratory, FP2M, CNRS FR 2036, Université de Paris, 75006, Paris, France

    Camille Pouchol

  2. Department of Computing, Electrical Engineering and Mathematical Sciences, Western Norway University of Applied Sciences, Bergen, Norway

    Olivier Verdier

Authors
  1. Camille Pouchol
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Olivier Verdier
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Camille Pouchol.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pouchol, C., Verdier, O. Statistical Model and ML-EM Algorithm for Emission Tomography with Known Movement. J Math Imaging Vis 63, 650–663 (2021). https://doi.org/10.1007/s10851-021-01021-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10851-021-01021-7

Keywords

Search

Navigation