Abstract
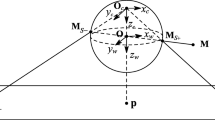
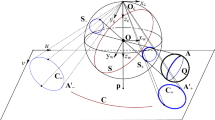
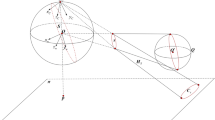
Omnidirectional vision sensors capture a wide field of view than can benefit many robotic applications. One type of omnidirectional vision sensor is the paracatadioptric. A paracatadioptric sensor combines a parabolic mirror and a camera inducing an orthographic projection. This combination provides a wide field of view while maintaining the single center of projection which is a desirable property of these sensors. Furthermore, lines are projected as circles on the paracatadioptric image plane. In contrast with traditional perspective cameras the image formation process of paracatadioptric sensors is no longer linear. However in this paper we present a model which is able to linearize it. This linearization is based on the fact that the paracatadioptric projection can be represented by a sphere inversion, that belongs to the conformal group \(\mathcal{R}^{n}\) which is isomorphic to the Lorentz group in \(\mathcal{R}^{n+1}\). Thus a nonlinear conformal transformation can be represented with an equivalent linear Lorenz transformation, which can be represented as a versor in the CGA. Therefore the present model can be applied algebraically not only to points, but also to point-pairs, lines, circles in the same way to all them and in a linear form. The benefits of the proposed method will be reflected on the development of complex applications that use paracatadioptric sensors.
Similar content being viewed by others
References
Baker, S., Nayar, S.: A theory of catadioptric image formation. In: Proc. Int. Conf. on Computer Vision, vol. IV, pp. 35–42 (1998)
Bayro-Corrochano, E.: Robot Perception and Action Using Conformal Geometric Algebra. Springer, Heidelberg (2005)
Bayro-Corrochano, E., López-Franco, C.: Omnidirectional vision: Unified model using conformal geometry. In: Proc. Eur. Conf. on Computer Vision, pp. 318–343 (2004)
Bayro-Corrochano, E., Reyes-Lozano, L., Zamora-Esquivel, J.: Conformal geometric algebra for robotic vision. J. Math. Imaging Vis. 24 (2006)
Benosman, R., Kang, S.B.: Panoramic Vision. Springer, Berlin (2000)
de Wit, E.C., Siciliano, B., Bastian, G.: Theory of Robot Control. Springer, Berlin (1997)
Dorst, L., Fontijne, D., Mann, S.: Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry. Morgan Kaufman, Heidelberg (2007)
Espiau, B., Chaumette, F., Rives, P.: A new approach to visual servoing in robotics. IEEE Trans. Robot. Autom. 8(3), 313–326 (1992)
Geyer, C., Daniilidis, K.: A unifying theory for central panoramic systems and practical implications. In: Proc. Eur. Conf. on Computer Vision, pp. 445–461 (2000)
Geyer, C., Daniilidis, K.: Paracatadioptric camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 24, 687–695 (2002)
Hestenes, D., Sobczyk, G.: Clifford Algebra to Ceometric Calculus. Reidel, Dordrecht (1984)
Hestenes, D., Li, H., Rockwood, A.: New algebraic tools for classical geometry. In: Sommer, G. (ed.) Geometric Computing with Clifford Algebra, vol. 24, pp. 3–26. Springer, Berlin (2001)
Li, H., Hestenes, D.: Generalized homogeneous coordinates for computational geometry. In: Sommer, G. (ed.) Geometric Computing with Clifford Algebra, vol. 24, pp. 27–60. Springer, Berlin (2001)
Malis, E., Chaumette, F., Boudet, S.: 2 1/2 d visual servoing. IEEE Trans. Robot. Autom. 15, 238–250 (1999)
Perwass, C.: Geometric Algebra with Applications in Engineering. Springer, Heidelberg (2009)
Svoboda, T., Pajdla, T., Hlavac, V.: Epipolar geometry for panoramic cameras. In: Proc. 5th European Conference on Computer Vision, pp. 218–231 (1998)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
López-Franco, C., Arana-Daniel, N. A Geometric Algebra Model for the Image Formation Process of Paracatadioptric Cameras. J Math Imaging Vis 43, 214–226 (2012). https://doi.org/10.1007/s10851-011-0305-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-011-0305-z