Abstract
In this paper, we propose and axiomatically characterize residual contractions, a new kind of contraction operators for belief bases. We establish that the class of partial meet contractions is a strict subclass of the class of residual contractions. We identify an extra condition that may be added to the definition of residual contractions, which is such that the class of residual contractions that satisfy it coincides with the class of partial meet contractions. We investigate the interrelations in the sense of (strict) inclusion among the class of residual contractions and other classes of well known contraction operators for belief bases.

Similar content being viewed by others
Notes
For a deep study of safe contraction functions see Rott and Hansson (2014).
In Fermé et al. (2008) these operators were designated by basic related-AGM base contractions.
We should note here also that, in Hansson (2017, p.38), the following alternative definition for partial meet contraction (equivalent to Definition 4) was proposed:
- 1.
If \(\not \vdash \alpha \), then \(A\div _{\gamma } \alpha =\bigcap \gamma ( {A}{ \perp } { \alpha })\) and
- 2.
If \(\vdash \alpha \), then \(A\div _{\gamma } \alpha =A\),
where \(\gamma \) is a function such that \(\gamma ( {A}{ \perp } { \alpha }) \subseteq {A}{ \perp } { \alpha }\), and if \( {A}{ \perp } { \alpha } \ne \emptyset \) then \(\gamma ( {A}{ \perp } { \alpha }) \ne \emptyset \).
This alternative definition is similar to the above definition of residual contraction, in the sense that for certain sentences (namely, for tautologies) the outcome of the contraction is defined explicitly (by A) without making use of the selection function \(\gamma \).
- 1.
We are thankful to the reviewer who pointed out this interesting similarity.
This proof uses Observation 8 whose proof is presented immediately after this lemma. However, this is not an issue because the result that is proven here is not used in the proof of that observation.
References
Alchourrón, C., Gärdenfors, P., & Makinson, D. (1985). On the logic of theory change: Partial meet contraction and revision functions. Journal of Symbolic Logic, 50, 510–530.
Alchourrón, C., & Makinson, D. (1981). Hierarchies of regulations and their logic. In R. Hilpinen (Ed.), New studies in deontic logic: Norms, actions, and the foundations of ethics (pp. 125–148). Berlin: Springer.
Alchourrón, C., & Makinson, D. (1985). On the logic of theory change: Safe contraction. Studia Logica, 44, 405–422.
Fermé, E., Garapa, M., & Reis, M. D. L. (2017). On ensconcement and contraction. Journal of Logic and Computation, 27(7), 2011–2042. https://doi.org/10.1093/logcom/exx008.
Fermé, E., & Hansson, S. O. (2011). AGM 25 years: Twenty-five years of research in belief change. Journal of Philosophical Logic, 40, 295–331.
Fermé, E., Krevneris, M., & Reis, M. (2008). An axiomatic characterization of ensconcement-based contraction. Journal of Logic and Computation, 18(5), 739–753.
Fuhrmann, A., & Hansson, S. O. (1994). A survey of multiple contraction. Journal of Logic, Language and Information, 3, 39–74.
Garapa, M. (2017). Advances on belief base dynamics. Ph.D. thesis, Universidade da Madeira.
Gärdenfors, P. (1988). Knowledge in flux: Modeling the dynamics of epistemic states. Cambridge: The MIT Press.
Gärdenfors, P., Makinson, D. (1988). Revisions of knowledge systems using epistemic entrenchment. In: M.Y. Vardi (ed.) Proceedings of the Second Conference on Theoretical Aspects of Reasoning About Knowledge, pp. 83–95. Morgan Kaufmann, Los Altos.
Grove, A. (1988). Two modellings for theory change. Journal of Philosophical Logic, 17, 157–170.
Hansson, S. O. (1989). New operators for theory change. Theoria, 55, 114–132.
Hansson, S. O. (1991a). Belief base dynamics. Ph.D. thesis, Uppsala University.
Hansson, S. O. (1991b). Belief contraction without recovery. Studia Logica, 50, 251–260.
Hansson, S. O. (1992). A dyadic representation of belief. In P. Gärdenfors (Ed.), Belief revision (pp. 89–121)., no. 29 in Cambridge tracts in theoretical computer science Cambridge: Cambridge University Press.
Hansson, S. O. (1993). Reversing the Levi identity. Journal of Philosophycal Logic, 22, 637–669.
Hansson, S. O. (1994). Kernel contraction. Journal of Symbolic Logic, 59, 845–859.
Hansson, S. O. (1999). A textbook of belief dynamics. Dordrecht: Theory Change and Database Updating. Applied Logic Series. Kluwer Academic Publishers.
Hansson, S. O. (2017). Descriptor revision., Trends in logic Berlin: Springer. https://doi.org/10.1007/978-3-319-53061-1.
Levi, I. (1991). The fixation of belief and its undoing: changing beliefs through inquiry. Cambridge: Cambridge University Press.
Rott, H. (2000). Two dogmas of belief revision. Journal of Philosophy, 97(9), 503–522.
Rott, H., & Hansson, S. (2014). Safe contraction revisited. In S. O. Hansson (Ed.), David Makinson on classical methods for non-classical problems, outstanding contributions to logic (Vol. 3, pp. 35–70). Dordrecht: Springer.
Williams, M. A. (1994). On the logic of theory base change. In C. MacNish (Ed.), Logics in artificial intelligence., no. 835 in Lecture Notes Series in Computer Science Berlin: Springer.
Acknowledgements
We wish to thank Rineke Verbrugge (the Associated Editor handling this paper), and the two reviewers of JoLLI for their valuable comments on a previous version, which have contributed to a significant improvement. This work was partially supported by FCT - Fundação para a Ciência e a Tecnologia through Projects UID/MAT/04674/2019 (CIMA) and PTDC/CCI-COM/30990/2017.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs
Appendix: Proofs
Lemma 1
(Hansson 1999) If \(A\subseteq B\subseteq Cn(A)\), then \(Cn(A)=Cn(B)\).
Lemma 2
(Hansson 1981, Observation 2.2) Let A be a set of sentences and \(\alpha \) a sentence. Then, \(A\perp \alpha =\emptyset \) if and only if \(\vdash \alpha \) (provided that the consequence operation Cn is compact).
Lemma 3
(Hansson 1999, Observation 1.39) Let A be a set of sentences and \(\alpha \) and \(\beta \) be sentences. Then the two following conditions are equivalent:
- 1.
\(A\perp \alpha = A\perp \beta \);
- 2.
For all subsets D of A: \(D \vdash \alpha \) if and only if \(D \vdash \beta \).
Lemma 4
Let A be a belief base. \(A\perp \alpha =\emptyset \) if and only if  .
.
Proof
(Right to left) Follows trivially by Observation 8.Footnote 6
(Left to right) Let \(A\perp \alpha =\emptyset \). Hence, by Lemma 2, \(\vdash \alpha \), from which it follows that  . \(\square \)
. \(\square \)
Proof
(Proof of Observation 8) Let \(X\in A\perp \alpha \). Hence \(X\subseteq A\) and \(X\not \vdash \alpha \). Let \(X'\subseteq A\) be such that \(Cn(X)\subset Cn(X')\). We intend to prove that \(X' \vdash \alpha \). From \(Cn(X)\subset Cn(X')\) it follows that there exists \(\delta \in X' {\setminus } X\). Let \(Y=Cn(X')\cap A\). It holds that \(X\subset X\cup \{\delta \}\subseteq Y\subseteq A\). Thus \(X\subset Y\subseteq A\). Therefore \(Y\vdash \alpha \) (since \(X\in A\perp \alpha \)). It holds that \(Y\subseteq Cn(X')\). Hence \(X'\vdash \alpha \). \(\square \)
Proof
(Proof of Observation 9) Let  . Hence \(Y\subseteq A\) and \(Y\not \vdash \alpha \). By the upper bound property it follows that there exists X such that \(Y\subseteq X\in A\perp \alpha \). From \(Y\subseteq X\) it follows, by monotony of Cn, that \(Cn(Y)\subseteq Cn(X)\). It holds that \(X\not \vdash \alpha \) and \(X\subseteq A\) (since \(X\in A\perp \alpha \)). Hence \(Cn(Y)\subset Cn(X)\) does not hold since
. Hence \(Y\subseteq A\) and \(Y\not \vdash \alpha \). By the upper bound property it follows that there exists X such that \(Y\subseteq X\in A\perp \alpha \). From \(Y\subseteq X\) it follows, by monotony of Cn, that \(Cn(Y)\subseteq Cn(X)\). It holds that \(X\not \vdash \alpha \) and \(X\subseteq A\) (since \(X\in A\perp \alpha \)). Hence \(Cn(Y)\subset Cn(X)\) does not hold since  . Therefore \(Cn(Y)=Cn(X)\). \(\square \)
. Therefore \(Cn(Y)=Cn(X)\). \(\square \)
Proof
(Proof of Observation 10) Let \(X\in A\perp \alpha \) and \(Y\subseteq X\) be such that \(Cn(X)=Cn(Y)\). From \(X\in A\perp \alpha \) it holds that \(X\not \vdash \alpha \) and \(X\subseteq A\). Hence \(Y\not \vdash \alpha \) and \(Y\subseteq A\). It remains to show that Y satisfies condition (3) of Definition 10. Let \(Z\subseteq A\) be such that \(Cn(Y)\subset Cn(Z)\). Hence \(Cn(X)\subset Cn(Z)\). Therefore there exists \(\delta \in Z{\setminus } X\). Let \(W=Cn(Z)\cap A\). Hence \(X\subset W\). Therefore \(W\vdash \alpha \) (since \(X\in A\perp \alpha \)). Thus \(Cn(Z)\vdash \alpha \). Thus, by iteration of Cn, \(Z\vdash \alpha \). \(\square \)
Proof
(Proof of Observation 11) (2) implies (1): Let  . It follows immediately from Definition 10 and (2) that
. It follows immediately from Definition 10 and (2) that  .
.
(1) implies (2): Suppose that (2) does not hold. Assume, without loss of generality, that there is some subset X of A such that \(X\not \vdash \alpha \) and \(X \vdash \beta \). By the residuum upper bound property it follows that there is some set \(X'\) such that  . On the other hand, from \(X\subseteq X'\) it follows that \(X'\vdash \beta \). Hence
. On the other hand, from \(X\subseteq X'\) it follows that \(X'\vdash \beta \). Hence  . This contradicts (1). \(\square \)
. This contradicts (1). \(\square \)
Proof
(Proof of Observation 12) Let  and Y be such that \(X\subseteq Y\subseteq Cn(X) \cap A\). Hence \(Y\subseteq A\) and \(X\subseteq Y\subseteq Cn(X)\). It follows from Lemma 1, that \(Cn(X)=Cn(Y)\). Therefore, \( Y \not \vdash \alpha \) and for any subset Z of A if \(Cn(Y)\subset Cn(Z)\), then \(Z\vdash \alpha \). Therefore
and Y be such that \(X\subseteq Y\subseteq Cn(X) \cap A\). Hence \(Y\subseteq A\) and \(X\subseteq Y\subseteq Cn(X)\). It follows from Lemma 1, that \(Cn(X)=Cn(Y)\). Therefore, \( Y \not \vdash \alpha \) and for any subset Z of A if \(Cn(Y)\subset Cn(Z)\), then \(Z\vdash \alpha \). Therefore  . \(\square \)
. \(\square \)
Proof
(Proof of Theorem 1) (Construction to postulates)
Let A be a belief base and \(\div \) be a residual contraction operator on A. Hence there is a selection function \(\gamma \) for A such that for all sentences \(\alpha \):
- 1.
if \(A\vdash \alpha \), then
 and
and - 2.
if \(A\not \vdash \alpha \), then \(A\div \alpha =A\).
We will show that \(\div \) satisfies success, inclusion, uniformity, vacuity, failure and weak relevance.
Success Let \(\not \vdash \alpha \). Hence, according to Lemmas 2 and 4,  . Therefore, by definition of a selection function,
. Therefore, by definition of a selection function,  is a non-empty subset of
is a non-empty subset of  . If \(A\not \vdash \alpha \), then \(A\div \alpha =A\), therefore \(A\div \alpha \not \vdash \alpha \). If \(A\vdash \alpha \), then
. If \(A\not \vdash \alpha \), then \(A\div \alpha =A\), therefore \(A\div \alpha \not \vdash \alpha \). If \(A\vdash \alpha \), then  , therefore \(A\div \alpha \not \vdash \alpha \) (since it holds, for any element X of
, therefore \(A\div \alpha \not \vdash \alpha \) (since it holds, for any element X of  , that \(X\not \vdash \alpha \)).
, that \(X\not \vdash \alpha \)).
Inclusion Let \(\alpha \in \mathcal {L}\). It follows trivially by the definition of \(\div \), if \(A\not \vdash \alpha \). Assume now that \(A\vdash \alpha \). We will consider two cases:
Case 1\(\vdash \alpha \). Hence, according to Lemmas 2 and 4,  . Therefore,
. Therefore,  . Hence \(A\div \alpha =A\).
. Hence \(A\div \alpha =A\).
Case 2\(\not \vdash \alpha \). Hence, according to Lemmas 2 and 4,  . Thus
. Thus  is a non-empty subset of
is a non-empty subset of  . Any element of
. Any element of  is a subset of A, hence any element of
is a subset of A, hence any element of  is also a subset of A. Therefore,
is also a subset of A. Therefore,  .
.
Uniformity Let \(\alpha , \beta \) be two sentences such that it holds for all subsets \(A'\) of A that \(\alpha \in Cn(A')\) if and only if \(\beta \in Cn(A')\). It follows from Observation 11 that  . Thus,
. Thus,  . We will consider two cases:
. We will consider two cases:
Case 1\(A\not \vdash \alpha \). Hence, by hypothesis, \(A\not \vdash \beta \). Therefore, \(A\div \alpha =A=A\div \beta \).
Case 2\(A\vdash \alpha \). Hence, by hypothesis, \(A \vdash \beta \). Therefore,  .
.
Vacuity Follows trivially by the definition of \(\div \).
Failure Let \(\vdash \alpha \). Hence, according to Lemmas 2 and 4,  . Therefore
. Therefore  . Thus
. Thus  .
.
Weak Relevance Let \(\beta \) be such that \( \beta \in A{\setminus } A\div \alpha \). Therefore, \(A\div \alpha \not = A\). Hence it holds that \(A\vdash \alpha \) and consequently that  . It also holds that
. It also holds that  . From \(\beta \not \in A\div \alpha \), it follows that there exists
. From \(\beta \not \in A\div \alpha \), it follows that there exists  such that \(\beta \not \in X\). Therefore \(A\div \alpha \subseteq X\). On the other hand, \(X\subseteq A\) (since
such that \(\beta \not \in X\). Therefore \(A\div \alpha \subseteq X\). On the other hand, \(X\subseteq A\) (since  ) and, since \(\beta \not \in X\), it follows that \(X\subseteq A{\setminus } \{\beta \}\). Furthermore, from
) and, since \(\beta \not \in X\), it follows that \(X\subseteq A{\setminus } \{\beta \}\). Furthermore, from  it follows that \(X\not \vdash \alpha \) and for any subset Y of A such that \(Cn(X)\subset Cn(Y)\) it holds that \(Y\vdash \alpha \).
it follows that \(X\not \vdash \alpha \) and for any subset Y of A such that \(Cn(X)\subset Cn(Y)\) it holds that \(Y\vdash \alpha \).
(Postulates to construction)
Let \(\div \) be an operator on A that satisfies success, inclusion, uniformity, vacuity, failure and weak relevance. Let \(\gamma \) be such that:
- (i)
\(\gamma (\emptyset )=\{A\}\);
- (ii)
If
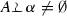 , then
, then 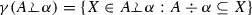 .
.
We need to show that: (1) \(\gamma \) is a (well-defined) function; (2) \(\gamma \) is a selection function; (3) for all \(\alpha \)
(3.1) if \(A\vdash \alpha \), then  and
and
(3.2) if \(A\not \vdash \alpha \), then \(A\div \alpha =A\).
(1) We must prove that for all \(\alpha , \beta \) if  then
then  .
.
Suppose that  . It follows trivially if
. It follows trivially if  . Assume now that
. Assume now that  . By Observation 11 it follows that for all subsets B of A: \(B\vdash \alpha \) if and only if \(B\vdash \beta \). Hence, uniformity yields that \(A\div \alpha =A\div \beta \). Hence, by definition of \(\gamma \), it holds that
. By Observation 11 it follows that for all subsets B of A: \(B\vdash \alpha \) if and only if \(B\vdash \beta \). Hence, uniformity yields that \(A\div \alpha =A\div \beta \). Hence, by definition of \(\gamma \), it holds that  .
.
(2) By definition \(\gamma (\emptyset )=\{A\}\). Hence, in order to prove that \(\gamma \) is a selection function it is sufficient to show that if  , then
, then  . That
. That  follows trivially by the definition of \(\gamma \). It remains to prove that
follows trivially by the definition of \(\gamma \). It remains to prove that  . Since
. Since  it must be the case that \(\not \vdash \alpha \). Thus by success, \(A\div \alpha \not \vdash \alpha \). It follows by inclusion that \(A\div \alpha \subseteq A\). By the residuum upper bound property there is some X such that
it must be the case that \(\not \vdash \alpha \). Thus by success, \(A\div \alpha \not \vdash \alpha \). It follows by inclusion that \(A\div \alpha \subseteq A\). By the residuum upper bound property there is some X such that  . Therefore, according to the definition of
. Therefore, according to the definition of  . Thus
. Thus  .
.
(3) Let \(\alpha \) be an arbitrary sentence. We will prove that (3.1) and (3.2) hold.
(3.1) \(A \vdash \alpha \). We will consider two cases:
Case 1\(\vdash \alpha \). Thus  . By definition of \(\gamma \) it follows that
. By definition of \(\gamma \) it follows that  . Hence
. Hence  . On the other hand, by failure\(A\div \alpha =A\). Therefore
. On the other hand, by failure\(A\div \alpha =A\). Therefore  .
.
Case 2\(\not \vdash \alpha \). Thus  . Therefore, as shown in (2),
. Therefore, as shown in (2),  . It follows from the definition of \(\gamma \) that \(A\div \alpha \) is a subset of every element of
. It follows from the definition of \(\gamma \) that \(A\div \alpha \) is a subset of every element of  . Thus
. Thus  . It remains to show that
. It remains to show that  . Let \(\beta \not \in A\div \alpha \). We will show that
. Let \(\beta \not \in A\div \alpha \). We will show that  . This is obvious if \(\beta \not \in A\). Assume now that \(\beta \in A\). Hence \(\beta \in A{\setminus } A\div \alpha \). It follows by weak relevance that there exists \(X\subseteq A{\setminus } \{\beta \}\) such that \(A\div \alpha \subseteq X\) and \(X\not \vdash \alpha \) but for all \(Y\subseteq A\) such that \(Cn(X)\subset Cn(Y)\) it holds that \(Y\vdash \alpha \). Hence
. This is obvious if \(\beta \not \in A\). Assume now that \(\beta \in A\). Hence \(\beta \in A{\setminus } A\div \alpha \). It follows by weak relevance that there exists \(X\subseteq A{\setminus } \{\beta \}\) such that \(A\div \alpha \subseteq X\) and \(X\not \vdash \alpha \) but for all \(Y\subseteq A\) such that \(Cn(X)\subset Cn(Y)\) it holds that \(Y\vdash \alpha \). Hence  . Therefore, by definition of \(\gamma \), it holds that
. Therefore, by definition of \(\gamma \), it holds that  . From \(\beta \not \in X\) it follows that
. From \(\beta \not \in X\) it follows that  .
.
(3.2) \(A\not \vdash \alpha \). Then by vacuity and inclusion it follows that \(A\div \alpha =A\). \(\square \)
Proof
(Proof of Observation 13) Let A be a belief base and \(\div \) an operator on A that satisfies relevance. Let \(\beta \in A{\setminus } A\div \alpha \). By relevance there exists X such that \(A\div \alpha \subseteq X\subseteq A\), \(X\not \vdash \alpha \) but \(X\cup \{\beta \}\vdash \alpha \). By the upper bound property there exists \(X\subseteq X'\) such that \(X'\in A\perp \alpha \). It must hold that \(\beta \not \in X'\) (otherwise it would follow that \(X'\vdash \alpha \)). On the other hand, by Observation 8,  . Therefore \(X'\subseteq A{\setminus } \{\beta \}\), \(A\div \alpha \subseteq X'\), \(X'\not \vdash \alpha \) and for any \(Y\subseteq A\) such that \(Cn(X')\subset Cn(Y)\) it holds that \(Y\vdash \alpha \). \(\square \)
. Therefore \(X'\subseteq A{\setminus } \{\beta \}\), \(A\div \alpha \subseteq X'\), \(X'\not \vdash \alpha \) and for any \(Y\subseteq A\) such that \(Cn(X')\subset Cn(Y)\) it holds that \(Y\vdash \alpha \). \(\square \)
Proof
(Proof of Observation 14) Let \(X\in A\perp \alpha \). By Observation 8 it follows that  . Assume now, by reductio ad absurdum, that there exists some
. Assume now, by reductio ad absurdum, that there exists some  such that \(X\subset Y\). From
such that \(X\subset Y\). From  it follows that \(Y\subseteq A\) and \(Y\not \vdash \alpha \). Hence, from \(Y\not \vdash \alpha \) and \(X\subset Y\subseteq A\), it follows (by condition (3) of Definition 2) that \(X\not \in A\perp \alpha \). Contradiction. Hence
it follows that \(Y\subseteq A\) and \(Y\not \vdash \alpha \). Hence, from \(Y\not \vdash \alpha \) and \(X\subset Y\subseteq A\), it follows (by condition (3) of Definition 2) that \(X\not \in A\perp \alpha \). Contradiction. Hence  .
.
Let  . Hence
. Hence  and there exists no \(Y'\) in
and there exists no \(Y'\) in  such that \(X'\subset Y'\). It follows from
such that \(X'\subset Y'\). It follows from  that \(X'\subseteq A\) and \(X'\not \vdash \alpha \). Let \(Z\subseteq A\) be such that \(X'\subset Z\). From \(X'\in \Gamma \) it follows that
that \(X'\subseteq A\) and \(X'\not \vdash \alpha \). Let \(Z\subseteq A\) be such that \(X'\subset Z\). From \(X'\in \Gamma \) it follows that  . Assume by reductio ad absurdum that \(Z\not \vdash \alpha \). Hence, by condition (3) of Definition 10, there exists \(Z'\subseteq A\) such that \(Cn(Z)\subset Cn(Z')\) and \(Z'\not \vdash \alpha \). From \(X'\subset Z\) it follows that \(Cn(X')\subseteq Cn(Z)\subset Cn(Z')\) and \(Z'\not \vdash \alpha \). Hence
. Assume by reductio ad absurdum that \(Z\not \vdash \alpha \). Hence, by condition (3) of Definition 10, there exists \(Z'\subseteq A\) such that \(Cn(Z)\subset Cn(Z')\) and \(Z'\not \vdash \alpha \). From \(X'\subset Z\) it follows that \(Cn(X')\subseteq Cn(Z)\subset Cn(Z')\) and \(Z'\not \vdash \alpha \). Hence  . Contradiction. Therefore \(Z\vdash \alpha \), and we can conclude that \(X'\in A\perp \alpha \). Therefore
. Contradiction. Therefore \(Z\vdash \alpha \), and we can conclude that \(X'\in A\perp \alpha \). Therefore  . \(\square \)
. \(\square \)
Proof
(Proof of Theorem 2) Let A be a belief base. We start by showing that every maximal residual contraction on A is a partial meet contraction on A.
Let  be a maximal selection function and let \(\div _{\gamma _{m}}\) be the maximal residual contraction based on \(\gamma _{m}\). Now let \(\gamma :\{A\perp \epsilon : \epsilon \in \mathcal {L}\}\longrightarrow \mathcal {P}(\mathcal {P}(A))\) be such that (for all \(\alpha \in \mathcal {L}\)):
be a maximal selection function and let \(\div _{\gamma _{m}}\) be the maximal residual contraction based on \(\gamma _{m}\). Now let \(\gamma :\{A\perp \epsilon : \epsilon \in \mathcal {L}\}\longrightarrow \mathcal {P}(\mathcal {P}(A))\) be such that (for all \(\alpha \in \mathcal {L}\)):

We will show that: (1) \(\gamma \) is a (well-defined) function; (2) \(\gamma \) is a selection function; (3) For all \(\alpha \), \(A\div _{\gamma _m}\alpha =A-_{\gamma }\alpha \), where \(-_{\gamma }\) is the partial meet contraction based on \(\gamma \).
(1) Let \(A\perp \alpha =A\perp \beta \). Combining Lemma 3 and Observation 11 we can conclude that  . Hence it follows from the definition of \(\gamma _m\) and from the fact that \(\gamma _m\) is a function, that \(\gamma (A\perp \alpha )=\gamma (A\perp \beta )\).
. Hence it follows from the definition of \(\gamma _m\) and from the fact that \(\gamma _m\) is a function, that \(\gamma (A\perp \alpha )=\gamma (A\perp \beta )\).
(2) Since if \(\vdash \alpha \), then  , it follows from the definition of \(\gamma \) that \(\gamma (\emptyset )=\gamma _{m}(\emptyset )=\{A\}\) (since \(\gamma _m\) is a selection function). It remains to show that if \(A\perp \alpha \not =\emptyset \), then \(\emptyset \not =\gamma (A\perp \alpha )\subseteq A\perp \alpha \). Assume that \(A\perp \alpha \not =\emptyset \), then
, it follows from the definition of \(\gamma \) that \(\gamma (\emptyset )=\gamma _{m}(\emptyset )=\{A\}\) (since \(\gamma _m\) is a selection function). It remains to show that if \(A\perp \alpha \not =\emptyset \), then \(\emptyset \not =\gamma (A\perp \alpha )\subseteq A\perp \alpha \). Assume that \(A\perp \alpha \not =\emptyset \), then  and, according to Lemma 4,
and, according to Lemma 4,  . Since \(\gamma _m\) is a selection function, it holds that
. Since \(\gamma _m\) is a selection function, it holds that  . Furthermore, since \(\gamma _m\) is maximal, if
. Furthermore, since \(\gamma _m\) is maximal, if  then there is no
then there is no  such that \(X\subset Y\). Therefore it follows by Observation 14 that
such that \(X\subset Y\). Therefore it follows by Observation 14 that  . Therefore \(\emptyset \not =\gamma (A\perp \alpha )\subseteq A\perp \alpha \).
. Therefore \(\emptyset \not =\gamma (A\perp \alpha )\subseteq A\perp \alpha \).
(3) If \(A\not \vdash \alpha \), then \(A\div _{\gamma _{m}}\alpha =A=A-_\gamma \alpha \). Now assume that \(A\vdash \alpha \). Then  .
.
Now we show that every partial meet contraction on A is a maximal residual contraction on A.
Let \(\gamma :\{A\perp \epsilon : \epsilon \in \mathcal {L}\}\longrightarrow \mathcal {P}(\mathcal {P}(A))\) be a selection function and let \(\div _{\gamma }\) be the partial meet contraction based on \(\gamma \). Now let  be such that (for all \(\alpha \in \mathcal {L}\)):
be such that (for all \(\alpha \in \mathcal {L}\)):

We will show that: (1) \(\gamma _m\) is a (well-defined) function; (2) \(\gamma _m\) is a maximal selection function; (3) For all \(\alpha \), \(A\div _{\gamma }\alpha =A-_{\gamma _m}\alpha \), where \(-_{\gamma _m}\) is the maximal residual contraction based on \(\gamma _m\).
(1) Let  . Combining Lemma 3 and Observation 11 we can conclude that \(A\perp \alpha =A\perp \beta \). Hence it follows from the definition of \(\gamma _m\) and from the fact that \(\gamma \) is a function, that
. Combining Lemma 3 and Observation 11 we can conclude that \(A\perp \alpha =A\perp \beta \). Hence it follows from the definition of \(\gamma _m\) and from the fact that \(\gamma \) is a function, that  .
.
(2) Since if \(\vdash \alpha \), then  , it follows, from the definition of \(\gamma _m\), that \(\gamma (\emptyset )=\gamma _{m}(\emptyset )=\{A\}\) (since \(\gamma \) is a selection function). It remains to show that if
, it follows, from the definition of \(\gamma _m\), that \(\gamma (\emptyset )=\gamma _{m}(\emptyset )=\{A\}\) (since \(\gamma \) is a selection function). It remains to show that if  , then:
, then:
(a)  ;
;
(b) If  , then there is no
, then there is no  such that \(X\subset Y\).
such that \(X\subset Y\).
Assume that  . Then, according to Lemma 4, \(A\perp \alpha \not =\emptyset \). Therefore, since \(\gamma \) is a selection function, it holds that \(\emptyset \not =\gamma (A\perp \alpha )\subseteq A\perp \alpha \). By Observation 8
. Then, according to Lemma 4, \(A\perp \alpha \not =\emptyset \). Therefore, since \(\gamma \) is a selection function, it holds that \(\emptyset \not =\gamma (A\perp \alpha )\subseteq A\perp \alpha \). By Observation 8 . Hence, since
. Hence, since  , we can conclude that (a) holds.
, we can conclude that (a) holds.
Next we prove (b). Let  . Since
. Since  it holds that \(X\in A\perp \alpha \). Therefore, it follows from Observation 14 that there is no
it holds that \(X\in A\perp \alpha \). Therefore, it follows from Observation 14 that there is no  such that \(X\subset Y\). Thus (b) holds.
such that \(X\subset Y\). Thus (b) holds.
(3) If \(A\not \vdash \alpha \), then \(A\div _{\gamma } \alpha =A=A-_{\gamma _{m}} \alpha \). Now assume that \(A\vdash \alpha \). Then  . \(\square \)
. \(\square \)
Rights and permissions
About this article
Cite this article
Garapa, M., Reis, M.D.L. Residual Contraction. J of Log Lang and Inf 29, 255–274 (2020). https://doi.org/10.1007/s10849-019-09296-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-019-09296-1




 and
and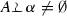 , then
, then 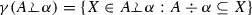 .
.