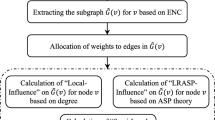
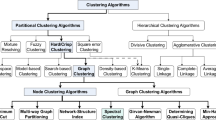
Abstract
We propose a graph model for mutual information based clustering problem. This problem was originally formulated as a constrained optimization problem with respect to the conditional probability distribution of clusters. Based on the stationary distribution induced from the problem setting, we propose a function which measures the relevance among data objects under the problem setting. This function is utilized to capture the relation among data objects, and the entire objects are represented as an edge-weighted graph where pairs of objects are connected with edges with their relevance. We show that, in hard assignment, the clustering problem can be approximated as a combinatorial problem over the proposed graph model when data is uniformly distributed. By representing the data objects as a graph based on our graph model, various graph based algorithms can be utilized to solve the clustering problem over the graph. The proposed approach is evaluated on the text clustering problem over 20 Newsgroup and TREC datasets. The results are encouraging and indicate the effectiveness of our approach.









Similar content being viewed by others
Notes
Probabilistic assignment of data object into several clusters is called soft assignment.
Minimizing − I(T;Y) is equivalent to maximizing I(T;Y).
Note that D KL [p(y|x) || p(y|t)] is not symmetric.
Each vertex has at least one edge with positive weight. For disconnected graphs, each component can be dealt with separately.
\(\sum_{x_j}\) ranges over \({\boldsymbol{X}}\) and corresponds to ∑ j .
\( I(X;Y) - I(T;Y) = \sum_{x,y} p(x,y) \log \frac{p(y|x)}{p(y)} - \sum_{y,t} p(y,t) \log \frac{p(y|t)}{p(y)} = \sum_{x,y,t} p(x,y,t) \left(\log \frac{p(y|x)}{p(y|t)} +\right.\)\( \left.\log \frac{p(y|t)}{p(y)}\right) - \sum_{x,y,t} p(x,y,t) \log \frac{p(y|t)}{p(y)} = \sum_{x} \sum_{t} p(x)p(t|x) \sum_{y} p(y|x) \log \frac{p(y|x)}{p(y|t)} = \sum_{x} \sum_{t} p(x)p(t|x)\)D KL [p(y|x) || p(y|t)]
\(\bar S\) is the complement of S. We follow the convention to utilize the symbol S to denote the subset in a partition.
S and \(\bar S\) corresponds to clusters.
Any hard assignment deviates from (6).
Although it is possible to deal with asymmetric matrix, we focus on symmetric one in this paper.
l corresponds to the number of dimension of the embedded subspace.
A dataset for new3 contains 2,200 data items. One run of iIB took more than 3 h, and we could not evaluate 100 runs for each value of β.
References
Agrawal, R., Gehrke, J., Gunopulos, D., & Raghavan P. (1998). Automatic subspace clustering of high dimensional data for data mining applications. In Proceedings of 1998 ACM-SIGMOD (pp. 94–105).
Akaike, H. (1973). Information theory and an extention of the maximum likelihood principle. In B. N. Petrov, & F. E. Csaki (Eds.), 2nd international symposium on information theory (pp. 267–281).
Bekkerman, R., Sahami, M., & Learned-Miller, E. (2006). Combinatorial Markov random fields. In Proceedings of the 17th European conference on machine learning (ECML-06) (pp. 30–41).
Belkin, M., & Niyogi, P. (2002). Laplacian eigenmaps for dimensionality reduction and data representation. Neural Computation, 15, 1373–1396.
Chung, F. (1997). Spectral graph theory. American Mathematical Society.
Cover, T., & Thomas, J. (2006). Elements of information theory. Wiley.
Dempster, A., Laird, N., & Rubin, D. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, 39(2), 1–38.
Dhillon, J., Mallela, S., & Modha, D. (2003). Information-theoretic co-clustering. In KDD 2003 (pp. 89–98).
Dhillon, J., & Modha, D. (2001). Concept decompositions for large sparse text data using clustering. Machine Learning, 42, 143–175.
Diestel, R. (2006). Graph theory. Springer.
Elghazel, H., Kheddouci, H., Deslandres, V., & Dussauchoy, A. (2008). A graph b-coloring framework for data clustering. Journal of Mathematical Modelling and Algorithms, 7(4), 389–423.
Elghazel, H., Yoshida, T., Deslandres, V., Hacid, M., & Dussauchoy, A. (2007). A new greedy algorithm for improving b-coloring clustering. In Proc. of the 6th workshop on graph-based representations (pp. 228–239).
Ester, M., Kriegel, H.-P., Sander, J., & Xu, X. (1996). A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of KDD-96 (pp. 226–231).
Frey, B. J. (1998). Graphical models for machine learning and digital communication. MIT Press.
Ghosh, J. (2003). Scalable clustering (pp. 341–364). Lawrence Erlbaum Associates.
Guénoche, A., Hansen, P., & Jaumard, B. (1991). Efficient algorithms for divisive hierarchical clustering with the diameter criterion. Journal of Classification, 8, 5–30.
Guha, S., Rastogi, R., & Shim, K. (1998). Cure: An efficient clustering algorithm for large databases. In Proceedings of the ACM SIGMOD conference (pp. 73–84).
Hacid, H., & Yoshida, T. (2010). Neighborhood graphs for indexing and retrieving multidimensional data. Journal of Intelligent Information Systems, 34, 93–11.
Halkidi, M., Batistakis, Y., & Vazirgiannis, M. (2002). Clustering validity checking methods: Part II. ACM SIGMOD Record, 31(3), 19–27.
Hansen, P., & Delattre, M. (1978). Complete-link cluster analysis by graph coloring. Journal of the American Statistical Association, 73, 397–403.
Hartigan, J., & Wong, M. (1979). Algorithm AS136: A k-means clustering algorithm. Journal of Applied Statistics, 28, 100–108.
Hartuv, E., & Shamir, R. (2000). A clustering algorithm based on graph connectivity. Information Processing Letters, 76, 175–181.
Irving, W., & Manlov, D. F. (1999). The b-chromatic number of a graph. Discrete Applied Mathematics, 91, 127–141.
Jain, A., Murty, M., & Flynn, T. (1999). Data clustering: A review. ACM Computing Surveys, 31, 264–323.
Li, T., Ma, S., & Ogihara, M. (2004). Entropy-based criterion in categorical clustering. In Proceedings of the 21st ICML (ICML-04) (pp. 536–543).
Maulik, U., & Bandyopadhyay, S. (2002). Performance evaluation of some clustering algorithms and validity indices. IEEE Transactions On Pattern Analysis and Machine Intelligence, 24(12), 1650–1654.
Muhlenbach, F., & Lallich, S. (2009). A new clustering algorithm based on regions of influence with self-detection of the best number of clusters. In Proc. of 2009 IEEE international conference on data mining (ICDM’09) (pp. 884–889).
Ng, R., & Han, J. (2002). Clarans: a method for clustering objects for spatial data mining. IEEE Transactions on Knowledge and Data Engineering, 14(5), 1003–1016.
Ogino, H., & Yoshida, T. (2010). Toward improving re-coloring based clustering with graph b-coloring. In Proceedings of PRICAI-2010 (pp. 206–218).
Pereira, F., Tishby, N., & Lee, L. (1993). Distributional clustering of English words. In Proc. of the 30th annual meeting of the Association for Computational Linguistics (pp. 183–190).
Quinlan, J. R. (1986). Induction of decision trees. Machine Learning, 1, 81–106.
Quinlan, J. R. (1993). C4.5: Programs For machine learning. Morgan Kaufmann.
Rissanen, J. (1978). Modeling by shortest data description methods in instance-based learning and data mining. Automatica, 14, 465–471.
Ristad, E. (1995). A natural law of succession. Technical Report CS-TR-495-95, Princeton University.
Roweis, S., & Saul, L. (2000). Nonlinear dimensionality reduction by locally linear embedding. Science, 290(22), 2323–2326.
Slonim, N. (2002). The information bottleneck: Theory and applications. PhD thesis, Hebrew University.
Slonim, N., Friedman, N., & Tishby, N. (2002). Unsupervised document classification using sequential information maximization. In SIGIR-02 (pp. 129–136).
Slonim, N., & Tishby, N. (2000). Agglomerative information bottleneck. In Advances in neural information processing systems (NIPS) (Vol.12, pp. 617–623).
Stoer, M., & Wagner, F. (1997). A simple min-cut algorithm. Journal of ACM, 44(4), 585–591.
Strehl, A., & Ghosh, J. (2002). Cluster ensembles—A knowledge reuse framework for combining multiple partitions. Journal of Machine Learning Research, 3(3), 583–617.
Tenenbaum, J., de Silva, J., & Langford, J. (2000). A global geometric framework for nonlinear dimensionality reduction. Science, 290(22), 2319–2323.
Tishby, N., Pereira, F., & Bialek, W. (1999). The information bottleneck method. In Proc. of the 37th allerton conference on communication and computation (pp. 368–377).
Toussaint, G. T. (2005). Geometric proximity graphs for improving nearest neighbor methods in instance-based learning and data mining. International Journal of Computational Geometry Applications, 15(2), 101–150.
Urquhart, R. (1982). Graph theoretical clustering based on limited neighbourhood sets. Pattern Recognition, 15(3), 173–187.
von Luxburg, U. (2007). A tutorial on spectral clustering. Statistics and Computing, 17(4), 395–416.
Zahn, C. T. (1971). Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Transactions on Computers, 20, 68–86.
Acknowledgements
We express sincere gratitude to the reviewers for their careful reading of the manuscript and for providing valuable suggestions to improve the paper. This work is partially supported by the grant-in-aid for scientific research (No. 20500123) funded by MEXT, Japan.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yoshida, T. A graph model for mutual information based clustering. J Intell Inf Syst 37, 187–216 (2011). https://doi.org/10.1007/s10844-010-0132-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10844-010-0132-5