A knowledge based freight management decision support system incorporating economies of scale: multimodal minimum cost flow optimization approach

Abstract

This study developed a framework incorporating economies of scale into the multimodal minimum cost flow problem. To properly account for the economies of scale observed in practice, we explicitly modelled economies of scale on quantity, distance and vehicle size in a given multimodal freight network. The proposed multimodal minimum cost flow problem formulation has concave equations due to economies of scale for quantity, non-linear equations due to economies of scale for both quantity and distance, and non-continuous equations due to the economies of scale for vehicle size. A genetic algorithm was applied to find acceptable route, mode, and vehicle size choices for the multimodal minimum cost flow problem. We demonstrated how the economies of scale influenced system (mode), route choices, and total cost under various demand/service capacity scenarios. Our results will lead into more realistic assessments of intermodal system by explicitly considering the three types of economies of scale.

Appendices

Appendix 1: Rationale to use GA

In this Appendix, the complexity of the proposed problem and the reason to use GA are demonstrated with a simple example. Assume r = 9 feasible routes (based on Fig. 2) from node 1 to node 3 via origin hub 5 and destination hub 6. Also, consider four types of cost functions: (1) simple constant cost functions (based on Eq. 1), (2) constant hub-discount cost functions (based on Eq. 2), (3) demand-dependent hub discount cost functions (based on Eq. 3), and (4) the proposed demand-dependent cost function with multiple sized vehicle options (based on Eq. 4 or, specifically, Eq. 6). The type of problem needed to estimate the number of cases to assign might be ∑ _r X ^r ₁₃ (a certain quantity) to 9 slots (where 0 ≤ r ≤ 9, X ^r _ij is a non-negative integer).

• When ∑ _r X ^r ₁₃  = 1, the four cases obviously have nine different costs for the nine options for assignment: ₉C₁. The feasible assignments are

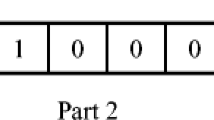
  • [1,0,0,0,0,0,0,0,0], [0,1,0,0,0,0,0,0,0], …[0,0,0,0,0,0,0,1,0], [0,0,0,0,0,0,0,0,1].

• When ∑ _r X ^r ₁₃  = 2, the four cases have 45 different costs for the nine options for assignment: 1 × ₉C₁ + 1 × ₉C₂. The feasible assignments are

  • [2,0,0,0,0,0,0,0,0], [0,2,0,0,0,0,0,0,0], …[0,0,0,0,0,0,0,2,0], [0,0,0,0,0,0,0,0,2] when one option (|r| = 1) is exclusively chosen, or

  • [1,1,0,0,0,0,0,0,0], [1,0,1,0,0,0,0,0,0], …[0,0,0,0,0,0,1,0,1], [0,0,0,0,0,0,0,1,1] when two options (|r| = 2) are chosen.

In the first (1) and second (2) cost functions, the total cost for all the other cases (i.e., ∑ _r X ^r ₁₃  = X, where X is a positive integer greater than 1) can be estimated through simple a arithmetic calculation once ∑ _r X ^r ₁₃  = 1 is separately estimated and saved. For example, the total cost for [1–8] can be easily estimated by multiplying 1,2,…,9 by [1,0,0,0,0,0,0,0,0], [0,1,0,0,0,0,0,0,0], …, [0,0,0,0,0,0,0,0,1], respectively. No further complexity is required. In the third (3) and fourth (4) cost functions, the total cost for ∑ _r X ^r ₁₃  = X should be independently estimated. In general, as one unit of demand increases, the total costs for all r should be estimated.

• When ∑ _r X ^r ₁₃  = 3, the four cases have nine different costs for the 9 options for assignment: 1 × ₉C₁ + 2 × ₉C₁ + 1 × ₉C₁. The feasible assignments are

  • [3,0,0,0,0,0,0,0,0], [0,3,0,0,0,0,0,0,0], …[0,0,0,0,0,0,0,3,0], [0,0,0,0,0,0,0,0,3] when one option (|r| = 1) is exclusively chosen, or

  • [2,1,0,0,0,0,0,0,0], [2,0,1,0,0,0,0,0,0], …[0,0,0,0,0,0,1,0,2], [0,0,0,0,0,0,0,1,2] when two options (|r| = 2) are chosen, or

  • [1,1,1,0,0,0,0,0,0], [1,1,0,1,0,0,0,0,0], …[0,0,0,0,0,1,0,1,1], [0,0,0,0,0,0,1,1,1] when three options (|r| = 3) are chosen.

In general, the number of the routing cases for one OD pair is β ₁ × ₉C₁ + β ₂ × ₉C ^···₂  + β ₉ ×₉C₉, where β _i is the sequence number in Pascal triangles (i = 1, 2,…, 9). Using this formula, the number of cases between any two nodes is $\sum\limits_{i = 1}^{9} {{}_{{\sum\limits_{r = 1}^{9} {X_{ij}^{r} } }}C_{i - 1} \times {}_{9}C_{i} }$. The number of cases are crucially dependent on $\sum\limits_{r = 1}^{9} {X_{ij}^{r} }$. For example, when $\sum\limits_{r = 1}^{9} {X_{ij}^{r} }$ = 10, 10², and 10³, the number of cases for a possible route combination are 7.6⁴, 3.8¹¹, and 2.6¹⁹, respectively. In addition, if we take the batch strategy into account, the number of cases is increased to $\left( {\sum\limits_{i = 1}^{9} {{}_{{\sum\limits_{r = 1}^{9} {X_{ij}^{r} } }}C_{i - 1} \times {}_{9}C_{i} } } \right) \times \left( {2^{N} - 1} \right)^{K}$, where N is the type of vehicle and K is the number of freight modes (see the algorithm for finding the minimum unit cost in the previous section). Furthermore, some inflows from the other nodes to hubs (e.g., X ^r ₂₄ for any r) possibly change $\varPsi_{hohd}^{{k_{2} }} (\sum\limits_{(i,j) \in A} {X_{ij}^{{k_{2} }} } ,d_{HoHd}^{{k_{2} }} ,S^{kv} ) \times d_{HoHd}^{{k_{2} }}$ (Eq. 6). For example, if 1 TEU shifts from r = 3 to r = 7 for X₁₃, it not only causes changes in the minimum unit costs ($\varPhi_{13}^{r}$) of the two shifted r for r = 3 and r = 7 but also changes in the minimum unit costs for all the other multimodal options (r). Therefore, the number of different cases in the function type (4) that are proposed in this study is $\left( {\sum\limits_{i = 1}^{9} {{}_{{\sum\limits_{r = 1}^{9} {X_{ij}^{r} } }}C_{i - 1} \times {}_{9}C_{i} } } \right) \times \left( {2^{N} - 1} \right)^{K} \times OD$, where OD is the number of OD pairs in a given network. Compared to function type (3), there are obviously fewer feasible assignments than for function type (4) due to non-road drayage. If we ignore non-road drayage, |r| is reduced from 9 to 3—that is, the number of cases related to non-road drayage is 6 (i.e., r = 3, 4, 5, 7, 8, and 9). In addition, if the batch strategy is not considered in cases with function type (3), the number of cases can be defined as $\left( {\sum\limits_{i = 1}^{3} {{}_{{\sum\limits_{r = 1}^{3} {X_{ij}^{r} } }}C_{i - 1} \times {}_{3}C_{i} } } \right) \times OD$, which is significantly less than the proposed function. Unless a meta-heuristic method such as GA is used, the proposed problem might not be solvable within a reasonable amount of time.

Appendix 2: GA-based heuristic algorithm

• Step 1: Initialize the parameters for given data such as generation number, population size, length of chromosome (which is equivalent to the number of decision variables in real-coded GA), OD demand matrix ($D_{ij}^{{}}$), OD distance matrix $d_{ij}^{k}$ for all (i,j) pairs and all modes in the cost function ($\varPsi_{ij}^{k} (X_{ij}^{k} ,d_{ij}^{k} ,S^{kv} )$), the lower bound (i.e., Constraint 4), and constant penalty (p).

• Step 2: Generate the initial population ($\tilde{X}_{ij}^{r}$) with two vectors: $\bar{X}_{ij}^{r}$ and $\hat{X}_{ij}^{r}$

  • Step 2.1: $\bar{X}_{ij}^{r}$ is a vector including N random real numbers, where N is the number of decision variables on arc (i,j), 0$\le$ $\bar{X}_{ij}^{r}$ $\le$ 1. Note: N is determined by the number of |r| and OD pairs (for example, N = 36 if |r| = 9 as in Fig. 2 and |OD| = 4 as in Table 2).

  • Step 2.2: $\hat{X}_{ij}^{r}$ is a vector including N random binary numbers, $\hat{X}_{ij}^{r}$ $\in$ [0, 1]. 1 is assigned as a component of $\hat{X}_{ij}^{r}$ if a random number is greater than 0.5; otherwise, 0 is assigned.

  • Step 2.3: The initial population ($\tilde{X}_{ij}^{r}$) is a vector placing $\bar{X}_{ij}^{r}$ and $\hat{X}_{ij}^{r}$ in the same raw in order.

    Note: the number of raw of $\tilde{X}_{ij}^{r}$ is 2N.

  • Step 2.4: Generate the matrix $\tilde{X}_{ij}^{r}$ until it reaches the maximum population size.

    Note: the matrix size of $\tilde{X}_{ij}^{r}$ should be 2N multiplied by the maximum population size. It is assumed that the number of decision variables should be even.

• Step 3: Update the initial population satisfying equality constraints (i.e., Constraint 1) for each arc (i,j) and generate the new population ($X_{ij}^{r}$).

• $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{X}_{ij}^{r}$ is the element-wise vector multiplication for the real number side ($\bar{X}_{ij}^{r}$) and the binary number side ($\hat{X}_{ij}^{r}$) of the initial population ($\tilde{X}_{ij}^{r}$).

• $X_{ij}^{r}$ = ($\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{X}_{ij}^{r} \times D_{ij}^{{}}$ /$\sum\limits_{r} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{X}_{ij}^{r} }$), where $\sum\limits_{r} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{X}_{ij}^{r} }$ is the sum of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{X}_{ij}^{r}$ for all r on (i,j) and $D_{ij}^{{}}$ is a given demand between i and j (TEU).

• Note: a raw vector of $X_{ij}^{r}$ is a candidate solution for (i,j) satisfying equality constraints and the size is N.

• Step 4: Calculate the objective function (i.e., Eq. 5) for the population ($X_{ij}^{r}$) with g = 1 where g is generation number;

• Save the objective function value for the gth population (Obj(g)).

• Step 5: Check for inequality constraints (Constraints 3 and 4);

• for each arc (i,j)

• If $\sum\limits_{{r_{k} }} {\sum\limits_{(i,j) \in A} {x_{ij}^{{r_{k} }} } } \le u_{{}}^{k}$ and $\sum\limits_{{r_{k} }} {\sum\limits_{(i,j) \in A} {x_{ij}^{{r_{k} }} } } \le Hub_{{}}^{k}$

• Obj(g) = Obj(g)

• Otherwise,

• Obj(g) = Obj(g) + Penalty (p)

• Step 6: Estimate the fitness function.

• Step 7: Increase the generation number (g = g + 1) and Run Reproduce, Crossover, Mutation, and Elitism for $X_{ij}^{r}$.

• Step 8: Return to Step 3 if g is less than the maximum number of generations.

Steps 2 and 3 are not normally included in prototypes of the GA procedure. These two steps are designed to generate the initial population and simultaneously ensure the equality constraint. These steps would be removed if another technique to handle equality constraints could be developed. In addition, Step 7 is not fully described here. For the details of Step 7, see two pioneer studies by Holland [9].