Malas notches

Abstract

This paper shows that the sufficient statistic approach to the welfare properties of income (and other) taxes does not easily extend to tax systems with notches, because with notches, changes in bunching induced by changes in tax rates have a first-order effect on tax revenues. In an income tax setting, we show that the marginal excess burden (MEB) of a change in the top rate of tax is given by the Feldstein (Rev Econ Stat 81(4):674–680, 1999) formula for the MEB of a proportional tax, plus a correction term. This formula applies even if there is tax evasion. These correction terms cannot be calculated just from knowledge of the elasticity of taxable income, and quantitatively, they can be large. An application to VAT is discussed; with a calibration to UK data, the MEB of the VAT is roughly three times what it would be if VAT was simply a proportional tax.

1 Introduction

In a recent survey, Chetty (2009a) argues that an important new development in public economics is the so-called sufficient statistic approach, which “derives formulas for the welfare consequences of policies that are functions of high-level elasticities rather than deep primitives” (Chetty 2009a, p. 451). In turn, this means that to assess the welfare properties of these policies, only these elasticities, rather than fully structural models, need to be estimated.¹

The sufficient statistic approach originated in a seminal paper by Feldstein (1999), who showed that the marginal excess burden (MEB) of a proportional income tax only depends on the behavioral responses to the tax via a sufficient statistic, the elasticity of taxable income (ETI). The ETI summarizes the response of a given household to changes in the tax rate, although these changes can be at several margins (hours, effort, etc.) Feldstein’s paper has given rise to a large literature devoted to obtaining empirical estimates of the ETI (Gruber and Saez 2002; Saez et al. 2012; Kleven and Schultz 2014; Weber 2014).

Subsequently, Saez (2001) and Saez et al. (2012) showed that the Feldstein formula for the MEB could be extended to the top rate of tax in a progressive piecewise-linear income tax system, and they also established formulae for the revenue and welfare-maximizing rate of tax. These formulae also have the sufficient statistic feature; specifically, they depend only on the ETI, a statistic of the income distribution, which is constant if the top tail of the income distribution is Pareto,² and possibly a welfare weight.

In this paper, we ask the question as to whether these sufficient statistic properties of key formulae also extend to tax systems with notches. Generally, a tax notch occurs when there is a discontinuous change in the tax liability as the tax base varies (Slemrod 2013; Kleven 2016).

In practice, we do see notches in several major kinds of taxes, and these are being increasingly studied in the empirical literature. For example, in Pakistan, there are notches of up to 5% in the personal income tax (Kleven and Waseem 2013), and in Ireland, an emergency income levy after the financial crisis had a notch of up to 4% (Hargaden 2015).³ There are small notches in the federal income tax in the USA, and larger notches induced by income-dependent entitlement to tax credits (Slemrod 2013). In Germany, there is a large notch in income tax generated by the Mini-Job program (Tazhitdinova 2018).⁴

Notches also exist in other major taxes. For example, notches are, or were until recently, present in housing transactions taxes in the UK and the USA (Best and Kleven 2013; Kopczuk and Munroe 2015). They also arise in the corporate income tax in Costa Rica (Bachas and Soto 2015). Slemrod (2013) notes that there are many examples of commodity tax notches, where a marginal change in some characteristic can change the product classification so as to produce a discrete change in the tax liability.⁵ Finally, as argued by Liu and Lockwood (2015), a VAT threshold can be thought of as a tax notch; a firm’s VAT liability changes discontinuously when its sales go over the registration threshold. Indeed, given the importance and near-ubiquity of VAT, this is probably the most important example of a tax notch.

We first study notches in the income tax setting of Saez (2010) and others, where households differ in ability or taste so that the disutility of generating taxable income varies across households. For simplicity, we assume a two-bracket tax, i.e., a tax with a lower rate below a threshold, and a higher rate above. In this setting, our first contribution is to derive an exact formula for the marginal excess burden (MEB) of the higher rate of tax. This formula is similar to Feldstein (1999)’s formula for the MEB of a proportional income tax, but includes a correction factor that captures the effect of the bunching response to an increase in the top rate tax on tax revenue.

The bunching response measures the change in the number of households bunching at the threshold to avoid paying the top rate of tax and is a property of the distribution of households. In what follows, to make it clear that this is a property of the distribution, we will henceforth call it the aggregate bunching response. It is thus distinct from the change in taxable income of a particular household induced by a change in the tax rate. The latter is measured by the elasticity of taxable income, and in what follows, we will call the second kind of response the individual response, as it pertains to a particular individual or household.⁶

Our main point is that with a notch, unlike the case of a kink, the aggregate bunching response affects tax revenue because with a notch, the tax schedule is discontinuous at the threshold. Specifically, an increase in the top rate of tax increases bunching just below the notch, which—due to the notch—lowers tax revenue, and thus raises the MEB. Moreover, this correction factor to the Feldstein formula, denoted C, cannot be expressed as a simple function of the usual sufficient statistics, i.e., the ETI and the Pareto parameter of the upper tail of the income distribution. It does depend on these variables, but it also depends on the lower rate of tax, the position of the notch, and a counterfactual, i.e., the earnings that the individual at the top of the interval (the top buncher) would choose if faced with the higher rate of tax. So, the sufficient statistic approach seems to break down with tax notches.

However, all is not lost. We show how the counterfactual earnings of the top buncher can be computed theoretically, using the indifference condition that the top buncher is indifferent between bunching and being above the notch. Alternatively, in any empirical study of bunching, it can be computed empirically, using the estimate of excess mass at the notch (the parameter B in Kleven and Waseem 2013). Thus, this paper is the first to show how bunching estimates at notches can be used to make welfare calculations.

Of course, if the correction factor turns out to be small, the Feldstein formula still provides a good approximation to the MEB. Our third contribution is to investigate whether this is the case. Calibrations show that the percentage error from using the Feldstein formula for the MEB can be very large. At baseline values, the marginal excess burden is underestimated by a factor of six. So, the conclusion is that at least in the income tax setting, the sufficient statistic approach is not practical.

We then turn to apply our approach to the VAT, which is the most empirically important example of a tax notch. We present a simple model of small traders who differ in productivity, and are subject to VAT at rate t above a threshold level of sales. We show that this model is formally equivalent to our income tax model, in the sense that registered firms above the threshold face an effective rate of VAT $t_{R}$ on value-added, and non-registered firms below the threshold face a lower but positive effective rate $t_{N}$.⁷

We then show that the MEB of an increase in the statutory rate of VAT is given by the Feldstein formula for a proportional tax plus a correction factor as in the income tax case. However, the details of the correction factor are more complex, because an increase in the statutory rate t increases both the effective rates $t_{R},t_{N}$. A calibration of the model shows that the proportional tax formula for the MEB of the VAT underestimates the true MEB by a factor of up to three.

Finally, it should be noted that in this paper, we take all parameters of the tax system, including the notch, as given, and only vary the top rate of tax. A broader question, to be addressed in future work, is whether a notch can ever be part of an optimal tax system.⁸

The remainder of the paper is arranged as follows. After the literature review in Sects. 2 and 3, we set up the model. Section 4 has the main analytical results for the income tax, Sect. 4.3 has an extension to tax evasion, and Sect. 5 the simulations. Section 6 deals with the extension to the VAT, and Sect. 7 concludes.

2 Related literature

This paper speaks to a number of related literatures. First, it is already known that due to externalities of one kind or another, the sufficient statistic approach has its limitations. Saez et al. (2012) give the examples of deductibility from income tax of charitable giving and mortgage interest payments for residential housing. In these cases, an increase in the marginal rate of tax will boost charity income and home ownership, respectively, which may be valuable objectives in themselves. Saez et al. (2012) call these classical externalities.⁹

Fiscal externalities, where the actions of the household generate additional revenue for the government and thus benefit other households, can also cause the sufficient statistic approach to fail, or at least require adjustment, but in these cases a simple change to the formula is sometimes possible. The analysis of income tax evasion of Chetty (2009b) is a case in point.¹⁰ As Gillitzer and Slemrod (2016) show, in this case the standard formula for the marginal efficiency cost of funds can be adjusted in the same way it must be adjusted for any fiscal externality, i.e., whenever a change in tax rates induces taxpayers to shift income to another tax. Our results are rather different to these cases of both classical and fiscal externalities. In our setting, there is no fiscal or other externality—rather, the sufficient statistic approach fails because the aggregate bunching response has a first-order effect on tax revenue. Indeed, in Sect. 4.3, we show our main qualitative results continue to apply in the presence of evasion, which makes the point that our argument is distinct from an externality one.

A second related literature is on VAT. Here, there are two distinct sets of related papers. First, there is a growing literature on the effect of VAT thresholds on firm behavior. Theoretical contributions include Keen and Mintz (2004), Kanbur and Keen (2014), and Liu and Lockwood (2015), and empirical studies include Liu and Lockwood (2015) and Harju et al. (2016). The theoretical work of Kanbur, Keen, and Mintz focuses on the optimal threshold of the VAT, holding the rate of tax fixed, and is thus complementary to this paper, which characterizes the MEB of an increase in the rate, holding the threshold fixed. In fact, we effectively ask the question of whether it is legitimate to ignore the threshold altogether when calculating the MEB of the VAT.

Therefore, our paper relates to a literature on the marginal excess burden of indirect taxes, including VAT (e.g., Ballard et al. 1985; Rutherford and Paltsev 1999). In these papers, when the marginal excess burden of VAT is calculated, it is always assumed that the VAT is a proportional tax, i.e., the VAT threshold is ignored. This paper shows that this simplifying assumption yields seriously biased estimates.

A third related literature is that on the MEB and welfare-maximizing taxes with kinks in the tax schedule. Here, we make a small contribution as a by-product of our main focus, which is on notches. In the case of kinks, it is generally understood that the marginal excess burden of the top rate of income tax, and the welfare-maximizing top rate depends via simple formulae, only on the elasticity of the ETI, and the Pareto statistic of the income distribution. However, there seems to be some confusion about the conditions required for this result. Saez et al. (2012) suggest that what is required is that assumption that “behavioral responses take place only along the intensive margin,” or more precisely that the aggregate bunching response of an increase in the top rate of tax is of second order relative to the extensive-margin response.¹¹ This assumption is very strong, as even with a kink, there is always a bunching response. Our Proposition 1 shows that this assumption is not necessary, because no matter what the size of the bunching response, the response has no effect on tax revenue, to first order, as the tax schedule is continuous. All that is required is that the distribution of taxpayer types is continuous, a standard assumption.

3 The model and preliminary results

3.1 Setup

We follow Saez (2010) in our setup. There are individual taxpayers indexed by a skill or taste parameter $n\in [{\underline{n}},{\overline{n}}]$, assumed continuously distributed in the population with distribution H(n) and density h(n). A type n individual has preferences over consumption c and taxable income z of the form

$$\begin{aligned} u(c,z;n)=c-\psi (z;n) \end{aligned}$$

(1)

where $\psi (z;n)$ is the disutility of earning income z. So, as utility is linear in c, we are assuming away income effects. We also assume:

A1. $\psi _{z}> 0,\psi _{zz}>0,\ \psi _{n},\psi _{nz}<0$.

A1 says that the cost of generating taxable income is strictly increasing and strictly concave in z. It also allows us to interpret a higher n as a higher skill level (i.e., higher wage), or a lower taste for leisure. In particular, the higher n, the lower the total and marginal disutility of generating a given amount of taxable income. Assumption A1 is satisfied, for example, by the iso-elastic specification of Saez (2010):

$$\begin{aligned} \psi (z;n)=\frac{n}{1+\frac{1}{e}}\left( \frac{z}{n}\right) ^{1+\frac{1}{e} } \end{aligned}$$

(2)

The budget constraint is $c=z-T(z)$, where $T(\cdot )$ is the tax function. So, a household’s utility over z is $u(z;n)=z-T(z)-\psi (z;n)$.

Finally, for future reference, define the optimal taxable income at tax rate t for a type n taxpayer to be;

$$\begin{aligned} z(1-t,n)\equiv \arg \max _{z \ge 0}\{(1-t)z-\psi (z;n)\} \end{aligned}$$

Generally, Assumption A1 does not imply that $z(1-t,n)>0$, so we allow for corner solutions with zero earnings, i.e., where the household does not work. However, in the iso-elastic case (2), there will always be an interior solution, as the marginal cost of z goes to zero with z. Note from A1 that if there is an interior solution $z(1-t,n)>0$, then $z_{1-t},z_{n}>0$, where subscripts denote derivatives. So, $z_{1-t}$ is the response of taxable income to the net-of-tax rate. Following the terminology introduced in the introduction, we call this the individual response to the tax.

3.2 Kinks and notches

For simplicity, we focus on a two-bracket tax, although our arguments apply straightforwardly to the case of the highest tax in a piecewise-linear tax system with any number of brackets. We will assume that the tax system is progressive; that is, the tax rate on incomes in the higher income bracket is strictly greater than the tax on incomes in the lower income bracket.

So, with a two-bracket tax, for a kink, the tax function is

$$\begin{aligned} T_{K}(z)=\left\{ \begin{array}{cc} t_{L}z, &{}\quad z\le z_{0}\\ t_{L}z_{0}+t_{H}(z-z_{0}), &{}\quad z>z_{0} \end{array}\right. \end{aligned}$$

(3)

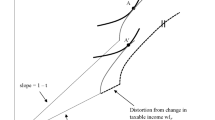
for $z_{0}>0,~t_{H}>t_{L}\ge 0$. That is, all income below the kink point $z_{0}$ is taxed at the lower rate $t_{L}$, and all income in excess of the kink is taxed at the higher rate. For a notch, the tax function is

$$\begin{aligned} T_{N}(z)=\left\{ \begin{array}{cc} t_{L}z, &{}\quad z\le z_{0}\\ t_{H}z, &{}\quad z>z_{0} \end{array}\right. \end{aligned}$$

(4)

with $t_{H}>t_{L}\ge 0$. That is, when taxable income is below $z_{0}$, a tax at rate $t_{L}$ is paid on all income, but when z is above $z_{0}$, a tax at rate $t_{H}$ is paid on all income.

Note here that we are studying what Kleven and Waseem (2013) call a proportional tax notch. The more general case is where there is also a pure notch, where a lump-sum tax or subsidy is also paid when earnings exceed $z_{0}$. We choose to focus on the proportional notch partly for simplicity, and partly because most of the empirical cases of notches discussed in the introduction are of this type.

3.3 Bunching

With either a kink or a notch, all types in an interval $n\in [n_{L},n_{H}]$ will bunch at taxable income $z_{0}$. In both cases, the lowest type who bunches is the one who is just willing to earn taxable income $z_{0}$ at the lower tax rate. So, $n_{L}$ is defined by the condition

$$\begin{aligned} z(1-t_{L},n_{L})=z_{0} \end{aligned}$$

(5)

With a kink, the highest type who bunches, $n_{H}$, is defined by the condition that the optimal choice of taxable income at tax $t_{H}$ is just $z_{0}$, i.e.,

$$\begin{aligned} z(1-t_{H};n_{H})=z_{0} \end{aligned}$$

(6)

With a notch, $n_{H}$ is defined by the condition that the $n_{H}$ type must be indifferent between staying at the notch and paying tax $t_{L}$, and choosing z optimally, and paying $t_{H}$ on all income. To write this indifference condition, we first define the indirect utility function

$$\begin{aligned} v(1-t;n)\equiv \max _{z \ge 0}\left\{ (1-t)z-\psi (z;n)\right\} \end{aligned}$$

Then, the condition defining $n_{H}$ can be written:

$$\begin{aligned} (1-t_{L})z_{0}-\psi (z_{0};n_{H})=v(1-t_{H};n_{H}) \end{aligned}$$

(7)

The left-hand side of (7) is utility when taxable income is constrained to be at the notch value $z_{0}$. Note that this indifference condition implies $z(1-t_{H},n_{H})>z_{0}$, because if $z(1-t_{H},n_{H} )<z_{0}$, the $n_{H}$-type could choose z optimally and stay below the notch.

3.4 The aggregate bunching response

Here, we study the effect of a change in $t_{H}$ on the mass of individuals who bunch, i.e., on the size of the interval $[n_{L},n_{H}]$. Note first from (5) that $n_{L}$ is unaffected by $t_{H}$ for both a kink and a notch. Next, in the kink case, we can calculate from (6) that

$$\begin{aligned} \frac{\partial n_{H}}{\partial t_{H}}=\frac{z_{1-t_{H}}}{z_{n}}>0 \end{aligned}$$

(8)

So, we have an aggregate bunching response to an increase in $t_{H}$, i.e., an increase in the tax rate above the kink makes going above the kink less attractive, and so more people bunch below the kink.

In the notch case, note that $v_{t}=-z$, where $v_{t}$ is the derivative of v with respect to t. Then, using this fact and the implicit function rule, we can calculate from (7) that

$$\begin{aligned} \frac{\partial n_{H}}{\partial t_{H}}=\frac{z(1-t_{H},n_{H})}{\psi _{n} (z_{0};n_{H})-\psi _{n}(z(1-t_{H},n_{H});n_{H})} \end{aligned}$$

(9)

Also, as $\psi _{nz}(z;n)<0$ and $z(1-t_{H},n_{H})>z_{0}$, we see that the denominator of (9) is positive, and consequently from (9):

$$\begin{aligned} \frac{\partial n_{H}}{\partial t_{H}}>0 \end{aligned}$$

(10)

So, again we see that there is an aggregate bunching response to a change in $t_{H}$; an increase in the tax rate above the notch makes going above the notch less attractive, and so more people bunch at the notch.

4 Main results

4.1 The effect of the aggregate bunching response on tax revenue

Here, we establish a key result that the effects of the aggregate bunching response on tax revenue with a kink and a notch are qualitatively different, being zero and negative respectively. With a kink, revenue can be written

$$\begin{aligned} R&= t_{L}\int _{{\underline{n}}}^{n_{L}}z(1-t_{L};n)h(n)dn+t_{L}(1-H(n_{L}))z_{0} \\&\quad +\,t_{H}\int _{n_{H}}^{{\overline{n}} }(z(1-t_{H};n)-z_{0})h(n)dn \end{aligned}$$

(11)

Note from the second and third terms in (11) that all households with $n\ge n_{L}$ pay tax at the lower rate on the first $z_{0}$ of earnings, and tax at the higher rate $t_{H}$ on the remainder.

So, in the kink case, the aggregate bunching effect on tax revenue, i.e., the effect of a change in $t_{H}$ on R via a change in $n_{H}$ is from (6) and (11):

$$\begin{aligned} \frac{\partial R}{\partial n_{H}}=-t_{H}(z(1-t_{H};n_{H})-z_{0})h(n_{H})=0 \end{aligned}$$

(12)

So, overall, with a kink, the effect of the aggregate bunching response on tax revenue is zero. This is simply due to the fact that a kinked tax schedule is continuous in z.

With a notch, revenue is

$$\begin{aligned} R&= t_{L}\int _{{\underline{n}}}^{n_{L}}z(1-t_{L};n)h(n)dn+t_{L}(H(n_{H})-H(n_{L}))z_{0} \\&\quad +\,t_{H}\int _{n_{H}}^{{\overline{n}} }z(1-t_{H};n)h(n)dn \end{aligned}$$

(13)

Comparing this to (11), we see a key difference. Because the higher rate applies to all income for those earning above $z_{0}$, the threshold $z_{0}$ no longer enters into the tax base for $t_{H}$, and so the size of the term on $z_{0}$ in the tax base for the lower rate of tax falls from $1-H(n_{L})$ to $H(n_{H})-H(n_{L})$, reflecting the fact that now only individuals below $n_{H}$ pay any tax at the lower rate.

Note from (13) that;

$$\begin{aligned} \frac{\partial R}{\partial n_{H}}=(t_{L}z_{0}-t_{H}z(1-t_{H};n_{H}))h(n_{H})<0 \end{aligned}$$

(14)

This is strictly negative as $t_{H}>t_{L}$, $z(1-t_{H};n_{H})>z_{0}$. So, in contrast to the kink case, the aggregate bunching effect on tax revenue R from an increase in $t_{H}$ is negative, as $\frac{\partial n_{H}}{\partial t_{H}}>0$ from (10). This is because a small increase in $n_{H}$ has two effects on revenue that are both negative. First, there is a discontinuity in the tax base; the earnings of these who now locate at the notch fall discontinuously from $z(1-t_{H};n_{H})$ to $z_{0}$. Second, there is a discontinuity in the tax rate applying to that base; all these earnings are taxed at a lower rate, $t_{L}$ rather than $t_{H}$.

So, we conclude:

Proposition 1

The effect of the bunching response on tax revenue is zero for a kink, but strictly negative for a notch.

This result is the key one that drives the rest of the paper. Proposition 1 also helps to clarify some confusion in the literature. As already noted, Saez et al. (2012) argue that for sufficient statistic formulae to apply in the kink case, what is required is that assumption that “behavioral responses take place only along the intensive margin,” or more precisely that the aggregate bunching response of an increase in the top rate of tax is of second order relative to the individual response. Proposition 1 shows that this assumption is not required, because no matter how large is $\frac{\partial n_{H}}{\partial t_{H}}$, $\frac{\partial R}{\partial n_{H}}=0$ in the kink case.

4.2 The marginal excess burden

Here, we derive a formula for the marginal excess burden (MEB) of $t_{H}$ when there is a notch and show that it can be written as the MEB of a proportional tax plus a correction factor. To define the MEB, note that due to quasi-linearity, the natural measure of welfare is the integral of indirect utilities, say W, plus revenue R, which is assumed to be redistributed as a lump-sum back to households when calculating the MEB. So,

$$\begin{aligned} \hbox{MEB}=-\frac{\mathrm{d}(W+R)/\mathrm{d}t_{H}}{\mathrm{d}R/\mathrm{d}t_{H}} \end{aligned}$$

(15)

The minus sign ensures that the marginal excess burden is measured as a positive number.

Generally, whether there is a kink or a notch, a simple envelope argument tells us that a change $\mathrm{d}t_{H}$ only has a direct effect on W; all indirect effects, via individual or aggregate bunching responses are zero, as households are optimizing. In turn, due to the assumption of a quasi-linear utility function, this direct effect is simply the total increase in tax paid at the higher rate, i.e., $\mathrm{d}t_{H}$ times the base of the higher rate of tax. That is, mathematically:

$$\begin{aligned} \frac{\mathrm{d}W}{\mathrm{d}t_{H}}=-\int _{n_{H}}^{{\overline{n}}}z(1-t_{H};n)h(n)\mathrm{d}n=-B_{H} \end{aligned}$$

(16)

where $B_{H}$ is the base of the higher rate of tax. Plugging (16) back into the MEB formula (15), dividing through by $B_{H}$, and rearranging, we get

$$\begin{aligned} \hbox{MEB}=\frac{1-E/F}{E/F},\quad E=\frac{t_{H}}{R}\frac{\mathrm{d}R}{\mathrm{d}t_{H}},\quad F=\frac{t_{H}B_{H}}{R} \end{aligned}$$

(17)

So, we see that we can always write the MEB in terms of an observable, F, the share of revenue raised by the top rate of tax, and E, the aggregate elasticity of revenue with respect to the top rate of tax. The problem with this characterization of the MEB is twofold.

First, it is not easy to credibly estimate E, as one must typically rely on cross-country data, and in that case, exogenous variation in the tax t is hard to find. For example, if the UK raised its top rate of tax $t_{H}$ from 40 to 50%—as actually happened in 2010—and revenue R rose by 5%, we cannot infer that the elasticity is 0.5 as other things are not equal. Moreover, the only plausible control group would be other similar countries, which are small in number, have their own changes in taxes, and so on.

Second, and more fundamentally, E will depend on both individual household responses to the top rate of tax $t_{H}$, and the distribution of income, and we wish to know how both these factors determine E. For the case of a kink, such a formula has been provided by Saez (2001) and is given in (23) below. It is the main objective of this paper to develop a similar formula for the case of a notch and explore its implications.

The first step in this exercise is to calculate the overall effect of an increase in $t_{H}$ on tax revenue R via the different channels. From (13), we have:

$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t_{H}}=B_{H}+ \begin{array}[c]{cc} \underbrace{t_{H}\left. \frac{\partial B_{H}}{\partial t_{H}}\right| _{n_{H}\text { const}}}+ &{} \underbrace{ \frac{\partial R}{\partial n_{H}} \frac{\partial n_{H}}{\partial t_{H}}}\\ \text { individual} &{} \text { aggregate bunching} \end{array} \end{aligned}$$

(18)

As before, $B_{H}$ is the base in which the higher rate of tax is levied.

So, (18) is composed of three terms, the mechanical effect $B_{H}$, and two behavioral effects on tax revenue, the individual and aggregate bunching effects. The individual effect on tax revenue is standard; it describes how the tax base changes because of changes in earnings, conditional on the taxpayer staying in the same tax bracket.

So, plugging (16), (18) back into the MEB formula (15), dividing through by $B_{H}$, multiplying by $1-t_{H}$, and noting that holding $n_{H}$ constant, $\frac{\partial B_{H}}{\partial (1-t_{H})}=-\frac{\partial B_{H} }{\partial t_{H}}$, we can establish the following result.

Proposition 2

With a tax notch, the marginal excess burden of the top rate of income tax is

$$\begin{aligned} \hbox{MEB}=\frac{t_{H}{\bar{e}}+C}{1-t_{H}(1+{\bar{e}})-C},\ C=-\frac{1-t_{H}}{B_{H}}\frac{\partial R}{\partial n_{H}}\frac{\partial n_{H}}{\partial t_{H}} \end{aligned}$$

(19)

where

$$\begin{aligned} {\bar{e}}=\left. \frac{1-t_{H}}{B_{H}}\frac{\partial B_{H}}{\partial (1-t_{H} )}\right| _{n_{H}\,\mathrm{const}}=\frac{1-t_{H}}{B_{H}}\int _{n_{H} }^{{\overline{n}}}\frac{\partial z(1-t_{H};n)}{\partial (1-t_{H})} h(n)\mathrm{d}n \end{aligned}$$

(20)

Here, ${\bar{e}}$ is the elasticity of the tax base $B_{H}$ with respect to the net-of-tax rate $1-t_{H}$, holding $n_{H}$ constant, and so is just the average ETI. Also, C is a correction factor, which captures the effect of a changing $n_{H}$, the aggregate bunching response, on the MEB, via its effect on revenue.

Note that (19) is the formula for the marginal excess burden of a proportional income tax, as shown by Feldstein (1999), plus a correction factor C. This is intuitive; all households above $n_{H}$ are paying tax at rate $t_{H}$ on all their income, so for these households, $t_{H}$ is indeed a proportional tax. So, as already remarked, the correction factor C just captures the effect of a changing $n_{H}$, the aggregate bunching response, on the MEB, via its effect on revenue.

As a next step, we would like to be able to investigate in more detail to what extent the correction factor C is quantitatively important. To do this, we make two standard assumptions. The first is that the disutility of income is iso-elastic, i.e., as in (2). In that case, all individuals have the same ETI, namely e, and so ${\bar{e}}=e$, a constant independent of $n_{H}$. The second is that the distribution of n is Pareto above $n_{H}$. We can then prove:¹²

Proposition 3

Assume iso-elastic utility (2), and that the distribution ofnis Pareto, with shape and scale parameters$a,{\underline{n}}$. Then, the MEB with a notch is

$$\begin{aligned} \hbox{MEB}=\frac{t_{H}e+C}{1-t_{H}(1+e)-C}, \end{aligned}$$

(21)

where

$$\begin{aligned} C=\frac{(t_{H}-t_{L}z_{0}/{\tilde{z}}_{H})(a-1)(1+e)}{1-\left( \frac{z_{0}}{{\tilde{z}}_{H}}\right) ^{(1+e)/e}}>0. \end{aligned}$$

(22)

Moreover, in (22), ${\tilde{z}}_{H}=n_{H}(1-t_{H})^{e}$ and $n_{H}$is defined by (7).

This result enables us to compare precisely how the MEB compares to the MEB in a kinked tax system. As shown for example, by Saez (2001), under our assumptions, the latter is

$$\begin{aligned} \hbox{MEB}_{K}=\frac{t_{H}ea}{1-t_{H}(1+ea)} \end{aligned}$$

(23)

Clearly, $\hbox{MEB}_{K}$ depends only on simple sufficient statistics; other than the tax rate $t_{H}$, it depends only on e, the individual elasticity of taxable income, and a, the shape parameter of the income distribution.

By contrast, from (22), it is clear that C is a more complex object. It depends not only on sufficient statistics e, a, and the top rate of tax, $t_{H}$, but also on other parameters of the tax system $t_{L},z_{0}$, and on ${\tilde{z}}_H$, which is the unconstrained earnings of the type $n_{H}$, given that they face the higher rate of tax.

So, there are two ways of solving for C. One is simply to compute C using formulae (22), (7), choosing calibrated values for $e,a,z_{0}$, and that is what we do in this paper. Alternatively, as shown by Kleven and Waseem (2013), in any empirical study of a notch, the earnings $n_{H}(1-t_{L})^e$ can be estimated. Specifically, $n_{H}(1-t_{L})^e$ is simply $z^{*}+\Delta z^{*}$ in the notation of their paper, where $z^{*}$ is the earnings notch and as explained there, $\Delta z^{*}/z^{*}$ can be estimated from excess bunching at the notch. Given this, ${\tilde{z}}_{H}$ can be recovered simply by multiplying $z^{*}+\Delta z^{*}$ by $(1-t_{H})^e/(1-t_{L})^e$, using the empirical estimate of e.

4.3 Tax evasion

Before turning to simulations with a calibrated version of our model, we consider how our results extend to the case where the taxpayer can evade, or shelter, some of her income at a resource cost. In this section, we briefly sketch the argument; the details are given in the Online Appendix.

We generalize our framework using Chetty (2009b). We now interpret z as reported income, and we denote by s income that is sheltered from the government. A type n individual now has preferences

$$\begin{aligned} u(c,s;n)=c-g(s)-\psi (z+s;n) \end{aligned}$$

(24)

Note two changes from (1). First, there is a cost of sheltering income from the tax authorities, captured by g; we assume that $g^{\prime },g^{\prime \prime }>0$. As Chetty (2009b) says, this could reflect the loss in profits from transacting in cash instead of electronic payments or the cost of choosing a distorted consumption bundle to avoid taxes. Second, the disutility of income depends on the sum of reported and sheltered income, i.e., $z+s$.

The budget constraint is

$$\begin{aligned} c=z+s-T(z)-a(s), \end{aligned}$$

(25)

whereas in Chetty (2009b), a(s) is the expected cost to the household of audit, which is assumed to be increasing and weakly convex in s. This captures any fines paid if s is detected by the tax authorities, times the probability of detection.¹³ Note that the tax paid depends only on reported income. The household maximizes (24) with respect to z, s subject to (25), giving rise to choice of reported income $z(1-t)$.

Then, the behavior of the household faced with a kink or a notch is qualitatively the same as before. That is, under either type of tax schedule, households in the bunching interval $[n_{L},n_{H}]$ keep z just at the threshold. In the case of a kink, $n_{L}$, $n_{H}$ are characterized by (5), (6) as before. In the case of a notch, (7) is modified to allow for the endogenous choice of sheltered income s. Given this, it is still the case that the effect on revenue R of a change in $n_{H}$ is zero in the kink case and negative in the notch case, as this simply follows from the (dis-)continuity of R in the kink (notch) case. So, Proposition 1 continues to hold.

Moreover, as shown in the Online Appendix, in the special case where there is no audit cost of evasion, i.e., $a \equiv 0$, Proposition 2 continues to hold. In the more realistic case where there is an audit cost, the MEB is equal to the MEB of a proportional tax plus two correction factors, one for the notch C as before, and one offsetting negative term capturing the fact that the audit cost is a transfer and thus lowers the MEB of the tax. As the first is positive and the second is negative, they have offsetting effects on the MEB.

5 Simulations

We have seen that the MEB of an increase in $t_{H}$ is given by the corresponding formula for a proportional tax $t_{H}$ plus a correction factor, C. Moreover, the MEB formula for a proportional tax is very simple, depending only on the intensive-margin elasticity e, and thus can easily be calculated.

So, a key question is whether we can get a good approximation to MEB by setting $C=0$, i.e., treating $t_{H}$ as a proportional tax. In this section, we investigate whether the MEB, calculated assuming that $t_{H}$ is a proportional tax, is a good approximation to the true MEB.

To do this, we need to calibrate the model. In particular, we require values for $e,a,t_{H},t_{L}$, and $z_{0}$. Our baseline parameter values are chosen as follows. Following Piketty and Saez (2013), we set $a=1.5$, and following Saez et al. (2012) and Kleven and Schultz (2014), we set $e=0.25$. Regarding the tax rates, we first set $t_{L}=0.2$, which is broadly in line with the average income and payroll tax paid by US households.¹⁴ It is also the basic rate of income tax in the UK. For the notch, we use the fact that notches in personal income tax, where they exist, are small. For example, Kleven and Waseem (2013) show that in the Pakistani income tax, the notch ranges between 2 and 5 percentage points. So, we will take our baseline notch $t_{H}-t_{L}=\Delta t=0.03$.

To choose ${\underline{n}},z_{0}$ we assume that only the top 20% of the population pay a higher rate of income tax, roughly the proportion in the UK. Define $n_{0}$ to be the skill level corresponding to taxable income just at the notch, i.e., $n_{0}(1-t_{L})^{e}=z_{0}$. This requires that 80% of the population have skills below $n_{0}$, i.e., $H\left( n_{0}\right) =1-\left( \frac{{\underline{n}}}{n_{0}}\right) ^{\alpha }=0.8$, or $\frac{{\underline{n}} }{n_{0}}=(0.2)^{1/1.5}=0.342$. Given that only the ratio $\frac{{\underline{n}} }{n_{0}}$ is determined, we set ${\underline{n}}=1$, so $n_{0}=2.924$. But then $z_{0}=2.924(0.8)^{0.25}=2.168$.

Finally, from (22), we need a value for $n_{H}$. Under the assumption (2), the indifference condition (7) reduces to

$$\begin{aligned} e(n_{H})^{-1/e}\left( z_{0}\right) ^{1+\frac{1}{e}}+n_{H}(1-t_{H} )^{1+e}-(1-t_{L})z_{0}(1+e)=0 \end{aligned}$$

(26)

Equation (26) has two roots, and we take the larger root to ensure that $n_{H}(1-t_{L})^{e}>z_{0}$. Finally, parameter values are chosen so that the denominator in (21) is positive, which is equivalent to $\mathrm{d}R/\mathrm{d}t_{H}>0$, i.e., that the tax rate is on the left side of the Laffer curve. This requires simply that the notch is greater than 0.0015.¹⁵

Figures 1 and 2 show both the true MEB, as given by (21), and the approximation, treating $t_{H}$ as a proportional tax, i.e., setting $C=0$ in (21). The former is denoted by MEB in the figures, and the latter by $\hbox{MEB}_{A}$.

Fig. 1

MEB as e varies

Fig. 2

MEB as a varies

The error in using $\hbox{MEB}_{A}$ at the baseline values can be read off from Fig. 1, setting $e=0.25$. It can be seen that true MEB is about 0.6, whereas the approximation is about 0.1. So, the error in using the proportional formula is about a factor of six. Figure 1 also shows that MEB is increasing in e, at a faster rate than $\hbox{MEB}_{A},$ so when $e=0.4$ for example, the error in using $\hbox{MEB}_{A}$ is almost an order of magnitude.

Figure 2 shows that MEB is also increasing in a, the Pareto parameter which measures (inversely) the size of the tail of the income distribution. As $\hbox{MEB}_{A}$ is independent of a, this means that the error in using $\hbox{MEB}_{A}$ is increasing in a.

6 An application to VAT

As remarked in the introduction, perhaps the most important example of a tax notch is the value-added tax. In this section, we present a simple model of the value-added tax, which is mathematically equivalent to the model developed above. We then calibrate the model using UK data from Liu and Lockwood (2015), to estimate the MEB from the VAT, taking into account bunching at the threshold.

6.1 The setup

Here, we briefly outline the setup of the model. A detailed exposition is in the Appendix. We consider a single industry with a fixed, large number of small traders producing a homogeneous good. Each small trader combines his own labor input with an intermediate input to produce output via a fixed-coefficients technology. An implication of this technology is that value-added is proportional to output. As in the income tax model, individual traders are indexed by a skill parameter and have a disutility of supplying labor of the same iso-elastic form as in (2).

Traders sell to final consumers, who have perfectly elastic demand for the good. This is analogous to the assumption made in the taxable income literature that the wage is fixed, i.e., labor demand is perfectly elastic at a fixed wage. The traders face a VAT system. If the trader is registered, he must charge VAT on sales at rate t, but can claim back VAT paid on the input. The trader must register for VAT if the value of sales exceeds the threshold but can register voluntarily even if this is not the case.

6.2 Trader payoffs, effective VAT rates, and bunching

Let n measure the skill of the trader. It is shown in the Appendix that the payoff of trader n can be written as a function of value-added z and the VAT system as follows;

$$\begin{aligned} u(z;n)=z-T(z)-\frac{n}{1+\frac{1}{e}}\left( \frac{z}{n}\right) ^{1+\frac{1}{e}} \end{aligned}$$

(27)

Here, T(z) is the amount of VAT paid by the trader. Moreover, T(z) can be written in terms of effective VAT rates:

$$\begin{aligned} T(z)=\left\{ \begin{array}{cc} t_{N}z, &{}\quad z\le z_{0}\\ t_{R}z, &{}\quad z>z_{0} \end{array}\right. ,\quad t_{R}=\frac{t}{(1+t)(1-\gamma )},\quad t_{N}=\frac{\gamma t}{1-\gamma }. \end{aligned}$$

(28)

Here, $t_{N},t_{R}$ are the effective VAT rates faced by non-registered and registered traders, respectively, on the value-added they generate. These depend on the statutory rate of VAT, t, the VAT threshold $z_{0}$, expressed as a level of value-added, above which the firm will register, and $\gamma$ which measures the intensity of the intermediate input in production.¹⁶

The idea is the following. First, if any intermediate input is used, i.e., $\gamma >0$, the trader is effectively taxed at rate $t_{N}$ even if his turnover is below the threshold and he does not register, because his input is subject to VAT. This effective rate is increasing in $\gamma$ and t. Second, if the trader’s value-added is above the threshold, he pays a rate $t_{R}$, which is also increasing in $\gamma$ and t. Finally, to rule out voluntary registration, we will assume that registration incurs a higher effective tax rate, i.e., $t_{R}>t_{N}$ which requires $1>(1+t)\gamma$.

Then, (27), (28) describe a utility function and a tax schedule as function of value-added z that are mathematically equivalent to the income tax model although, obviously, the economic interpretation of z is different. From this equivalence, we can infer the following. Faced with the tax schedule (28), all traders in the interval $n\in [n_{L},n_{R}]$ will bunch at the VAT threshold $z_{0}$. Moreover, $n_{L}=z_{0}/(1-t_{N})^{e}$, and $n_{R}$ solves (7) with $t_{H},t_{L}$ replaced by $t_{R},t_{N}$.

6.3 The marginal excess burden of the VAT

Here, we use the mathematical equivalence of the VAT and income tax models to move swiftly to a formula for the MEB of the VAT. First, let $z(1-t;n)=(1-t)^{e}n$ be the value-added chosen by an unconstrained firm facing tax t. Then, it is shown in A.2 that the revenue from the VAT is as in (13), with $t_{H},t_{L}$ replaced by $t_{R},t_{N}$. Then, the revenue from the VAT can be written compactly as

$$\begin{aligned} R=t_{N}B_{N}+t_{R}B_{R} \end{aligned}$$

(29)

In (29), the bases on which $t_{N}, t_{R}$ are levied are the value-added of non-registered and registered traders, respectively, i.e.,

$$\begin{aligned} B_{N}&= \int _{{\underline{n}}}^{n_{N}}(1-t_{N})^{e}nh(n)dn+z_{0}(H(n_{R} )-H(n_{N})), \\ B_{R}&= \int _{n_{R}}^{{\overline{n}}}(1-t_{R})^{e}nh(n)dn \end{aligned}$$

(30)

Now note that a change in the statutory rate t of VAT will change both effective tax rates $t_{N},t_{R}$ unless $\gamma =0$, i.e., no intermediate inputs are used. This is of course, analogous to a reform that changes both $t_{H}$ and $t_{L}$ in the income tax model. So, for the VAT, the formula for the MEB becomes somewhat more complex. To present the formula for the MEB in this case, we need a few more definitions. First, from (30), the intensive-margin elasticities of $B_{R},B_{N}$ with respect to the net-of-tax rate are

$$\begin{aligned} \frac{1-t_{R}}{B_{R}}\left. \frac{\partial B_{R}}{\partial t_{R}}\right| _{n_{R}\text { const}}=e,\ \frac{1-t_{N}}{B_{N}}\left. \frac{\partial B_{N} }{\partial (1-t_{N})}\right| _{n_{N}~\text {const}}=e\phi , \end{aligned}$$

(31)

where

$$\begin{aligned} \phi =\frac{\int _{{\underline{n}}}^{n_{N}}z(1-t_{N};n)h(n)\mathrm{d}n}{B_{N} }<1 \end{aligned}$$

(32)

The term $\phi$ captures a new effect of bunching; with bunching, a mass $H(n_{R})-H(n_{N})$ of the non-registered firms that are bunching are unresponsive to a change in the rate of VAT, which lowers the aggregate intensive-margin elasticity of the tax base $B_{N}$ with respect to $t_{N}$.¹⁷

Moreover, recall that an increase in t causes both $t_{N}$ and $t_{R}$ to increase, so

$$\begin{aligned} \theta =\frac{\frac{B_{R}}{1-t_{R}}\frac{\partial t_{R}}{\partial t}}{\frac{B_{R}}{1-t_{R}}\frac{\partial t_{R}}{\partial t}+\frac{B_{N}}{1-t_{N} }\frac{\partial t_{N}}{\partial t}} \end{aligned}$$

(33)

measures the importance of a change in $t_{R}$ on tax revenue relative to a change in $t_{N}$. Armed with these new definitions, we can state our result, which is proved in the Appendix.

Proposition 4

Assume that the distribution of sales is Pareto, with shape and scale parameters$a,{\underline{n}}$. Then, the MEB of the VAT is

$$\begin{aligned} \hbox{MEB}=\frac{\tau \varepsilon +C}{1-\tau (1+\varepsilon )-C} \end{aligned}$$

(34)

where

$$\begin{aligned} \tau =(1-\theta )t_{N}+\theta t_{R},\quad \varepsilon =\frac{(1-\theta )t_{N} \phi +\theta t_{R}}{(1-\theta )t_{N}+\theta t_{R}}e \end{aligned}$$

(35)

and finally the correction factor is

$$\begin{aligned} C=-\frac{\frac{\partial R}{\partial n_{R}}\left( \frac{\partial n_{R} }{\partial t_{N}}\frac{\partial t_{N}}{\partial t}+\frac{\partial n_{R} }{\partial t_{R}}\frac{\partial t_{R}}{\partial t}\right) }{\frac{B_{R} }{1-t_{R}}\frac{\partial t_{R}}{\partial t}+\frac{B_{N}}{1-t_{N}} \frac{\partial t_{N}}{\partial t}} \end{aligned}$$

(36)

So, we note now that bunching impacts the calculation of the MEB in two ways. First, as before, there is a correction factor C in (34). The correction factor is more complex than in the income tax case. The reason for the additional complexity is clear from (36); an increase in t now increases both $t_{R},t_{N}$ and in turn, both of these effective taxes affect $n_{R}$, the top of the bunching interval, and thus revenue. An explicit formula for C in terms of parameters can be derived as in (22) above; this is done in the Online Appendix.

In addition, there is a second, new effect of bunching in (35). Bunching dampens the intensive-margin response to a change in t, because at a fixed $n_{N},n_{R}$, firms in this interval will not adjust their sales in response to a change in t. This is captured by the term $\phi$ which lowers the intensive-margin response from e to $\varepsilon$.

An interesting special case is where the small traders do not use any intermediate input, so. i.e., $\gamma =0$. Then from (28), $t_{N}=0$, $t_{R}=\frac{t}{1+t}$, so (34) simplifies to

$$\begin{aligned} \hbox{MEB}=\frac{\frac{t}{1+t}e+C}{1-\frac{t}{1+t}(1+e)-C} \end{aligned}$$

(37)

It can be checked that in this case, C is given by the explicit formula (22), replacing $t_{H},t_{L}$ by $t_{R},0$, respectively.

6.4 Simulations

Here, we calibrate the VAT model and plot the true MEB in (34) and an approximation to the MEB as parameters vary.¹⁸ The approximation is the one treating VAT as a proportional tax, i.e., setting $C=0$ in (37), which gives

$$\begin{aligned} \hbox{MEB}_{A}=\frac{\frac{t}{1+t}e}{1-\frac{t}{1+t}(1+e)} \end{aligned}$$

The parameters are calibrated as follows. In the UK, the statutory rate of VAT is 20%, so $t=0.2.$ Liu and Lockwood (2015) calculate that for the universe of firms in the UK that file a corporate tax return, $\gamma =0.45$. This gives $t_{N}=0.16$, $t_{R}=0.30$.

Next, define $n_{0}$ to be the productivity level corresponding to turnover just at the threshold, i.e., $n_{0}(1-t_{N})^{e}=z_{0}$. From Liu and Lockwood (2015), 62.5% of firms are below the threshold. So, $\frac{{\underline{n}} }{n_{0}}$ must satisfy $H\left( n_{0}\right) =1-\left( \frac{\underline{n}}{n_{0}}\right) ^{1.2}=0.625$, or $\frac{{\underline{n}}}{n_{0} }=(0.375)^{1/1.2}=0.442$. Given that only the ratio $\frac{{\underline{n}} }{n_{0}}$ is determined, we set ${\underline{n}}=1$, so $n_{0}=2.26$. But then $z_{0}=2.53(0.84)^{0.25}=2.164$.

Finally, we need a value for a. A prior question is whether the “upper tail” of the distribution of firm sales y is well described by a Pareto distribution. In the case of personal incomes, a Pareto distribution of the upper tail is widely accepted, but less is known about firms. In the USA, there is evidence that the size distribution of firms as measured by sales is Pareto (Luttmer 2007), and Luttmer estimates a value for the USA of $a=1.06$. In the Online Appendix, we provide evidence that this is also the case for the UK, using firm sales from administrative data on corporate tax returns. We show that for firms above the VAT threshold, the estimate a is about 1.2. So, this is the figure we will use in the simulations.

Our results are given in Figs. 3 and 4. Here, we see that the true MEB is about three times higher than the approximation. Also, the true MEB is increasing in both e and a. This difference is much smaller than in the income tax case, which is due partly to the lower value of a in the VAT case. Indeed, we can see in Fig. 4 that the accuracy of the approximation $\hbox{MEB}_{A}$ falls rapidly as a rises, because MEB is increasing in a whereas $\hbox{MEB}_{A}$ is independent of a.

Fig. 3

MEB of VAT as e varies, $\gamma =0.45$

Fig. 4

MEB of VAT as a varies, $\gamma =0.45$

7 Conclusions

This paper shows that the sufficient statistic approach to the welfare properties of income (and other) taxes does not easily extend to tax systems with notches, because with notches, changes in aggregate bunching induced by changes in tax rates have a first-order effect on tax revenues. In an income tax setting, we showed that the MEB of a change in the top rate of tax is given by the Feldstein (1999) formula for the MEB of a proportional tax, plus a correction term. This formula also applies when the model is extended to allow for tax evasion. These correction terms can be computed empirically, using an estimate of excess mass at the notch. Quantitatively, these correction terms can be very large.

An application to VAT was also discussed. A simple model of small traders who differ in productivity and are subject to VAT at rate t above a threshold level of sales was shown to be formally equivalent to the income tax model. We showed that the MEB of an increase in the statutory rate of VAT is given by the Feldstein formula for a proportional tax plus a correction factor as in the income tax case. With a calibration to UK data, the MEB of the VAT is roughly three times what it would be if VAT was simply a proportional tax.

Appendix

1.1 Proofs of Propositions

Proof of Proposition 3

Under the assumptions made in this Proposition, ${\bar{e}}=e$. So, the MEB formula (21) follows from (19). It remains to derive formula (22) for C. From (9), noting that

$$\begin{aligned} \psi _{n}=-\frac{1}{1+e}\left( \frac{z}{n}\right) ^{1+1/e}. \end{aligned}$$

(38)

and $z(1-t;n)=(1-t)^{e}n$, we have

$$\begin{aligned} \frac{\partial n_{H}}{\partial t_{H}}=\frac{(1-t_{H})^{e}n_{H}(1+e)}{(1-t_{H})^{1+e}-\left( \frac{z_{0}}{n_{H}}\right) ^{1+1/e}} \end{aligned}$$

(39)

Next, from (14) and (16), using the fact that $z(1-t;n)=(1-t)^{e} n$, we have

$$\begin{aligned} \frac{1}{B_{H}}\frac{\partial R}{\partial n_{H}} =\frac{(t_{L}z_{0}-t_{H}(1-t_{H})^{e}n_{H})h(n_{H})}{(1-t_{H})^{e} \int _{n_{H}}^{{\overline{n}}}nh(n)dn} \end{aligned}$$

(40)

So, plugging (39), (40) into the formula for C in (19), we have:

$$\begin{aligned} C =\frac{(1-t_{H})(t_{H}(1-t_{H})^{e}n_{H}-t_{L}z_{0})}{(1-t_{H} )^{e}E[n\left| n\ge n_{H}\right. ]}\frac{h(n_{H})}{\left( 1-H(n_{H})\right) }\frac{n_{H}(1+e)}{(1-t_{H})^{1+e}-\left( \frac{z_{0} }{n_{H}}\right) ^{1+1/e}} \end{aligned}$$

where we have used $\int _{n_{H}}^{{\overline{n}} }nh(n)dn=E[n\left| n\ge n_{H}\right. ]\left( 1-H(n_{H})\right)$ in (41).

Now, given that n follows a Pareto distribution with shape and scale parameters $a,{\underline{n}}$, we also know that

$$\begin{aligned} E[n\left| n\ge n_{H}\right. ]=\frac{an_{H}}{a-1},\quad \frac{h(n)}{1-H(n)}=\frac{a}{n} \end{aligned}$$

(41)

Plugging (41) into (41), we get:

$$\begin{aligned} C=\frac{(1-t_{H})(t_{H}(1-t_{H})^{e}-t_{L}z_{0}/n_{H})(a-1)(1+e)}{ (1-t_{H})^{1+e}-\left( \frac{z_{0}}{n_{H}}\right) ^{1+1/e} } \end{aligned}$$

(42)

Then, using the definition ${\tilde{z}}_{H}=n_{H}(1-t_{H})^e$ to eliminate $n_{H}$ in (42), and rearranging, we get (22) as required. $\square$

Proof of Proposition 4

Let $B_{N},B_{R}$ be the bases of the effective taxes $t_{N},t_{R}$ defined in (30). Then from (29), (30) and remembering that a change in the statutory rate of VAT t changes $t_{N},t_{R}$ via (28), we have:

$$\begin{aligned} \frac{\mathrm{d}W}{\mathrm{d}t}= & {} -\left( \frac{\partial t_{N}}{\partial t}B_{N}+\frac{\partial t_{R}}{\partial t}B_{R}\right) \end{aligned}$$

(43)

$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}= & {} \frac{\partial t_{N}}{\partial t}\left( B_{N}+t_{N}\left. \frac{\partial B_{N}}{\partial t_{N}}\right| _{n_{R}\text { const}}\right) +\frac{\partial t_{R}}{\partial t}\left( B_{R}+t_{R}\left. \frac{\partial B_{R}}{\partial t_{R}}\right| _{n_{R}\text { const}}\right) -C^{\prime } \end{aligned}$$

(44)

where

$$\begin{aligned} C^{\prime }=-\frac{\partial R}{\partial n_{R}}\left( \frac{\partial t_{N} }{\partial t}\frac{\partial n_{R}}{\partial t_{N}}+\frac{\partial t_{R} }{\partial t}\frac{\partial n_{R}}{\partial t_{R}}\right) \end{aligned}$$

(45)

So, plugging (43), (44) into (15), we have, after rearrangement

$$\begin{aligned} \hbox{MEB}&=-\frac{\mathrm{d}(W+R)/\mathrm{d}t}{\mathrm{d}R/\mathrm{d}t} \\&=\frac{\frac{B_{N}}{1-t_{N}}\frac{\partial t_{N}}{\partial t}t_{N}\left( \frac{1-t_{N}}{B_{N}}\left. \frac{\partial B_{N}}{\partial (1-t_{N} )}\right| _{n_{R}\text { const}}\right) +\frac{B_{R}}{1-t_{R}} \frac{\partial t_{R}}{\partial t}t_{R}\left( \frac{1-t_{R}}{B_{R}}\left. \frac{\partial B_{R}}{\partial (1-t_{R})}\right| _{n_{R}\text { const} }\right) +C^{\prime }}{\frac{B_{N}}{1-t_{N}}\frac{\partial t_{N}}{\partial t}\left( 1-t_{N}-t_{N}\frac{1-t_{N}}{B_{N}}\left. \frac{\partial B_{N} }{\partial t_{N}}\right| _{n_{R}\text { const}}\right) +\frac{B_{R} }{1-t_{R}}\frac{\partial t_{R}}{\partial t}\left( 1-t_{R}-t_{R}\frac{1-t_{R} }{B_{R}}\left. \frac{\partial B_{R}}{\partial t_{R}}\right| _{n_{R}\text { const}}\right) -C^{\prime }} \\&=\frac{\frac{B_{N}}{1-t_{N}}\frac{\partial t_{N}}{\partial t}e\phi +\frac{B_{R}}{1-t_{R}}\frac{\partial t_{R}}{\partial t}t_{R}e+C^{\prime } }{\frac{B_{N}}{1-t_{N}}\frac{\partial t_{N}}{\partial t}(1-t_{N} (1+e\phi ))+\frac{B_{R}}{1-t_{R}}\frac{\partial t_{R}}{\partial t} (1-t_{R}(1+e))-C^{\prime }} \end{aligned}$$

(46)

where in the last line, we have used (31). So, dividing top and bottom of (46) by $\frac{B_{R}}{1-t_{R}}\frac{\partial t_{R}}{\partial t}+\frac{B_{N}}{1-t_{N}}\frac{\partial t_{N}}{\partial t}$ and using the definition of $\theta$ from (33), and the definition of C from (36), we get

$$\begin{aligned} \hbox{MEB}=\frac{(1-\theta )t_{N}e\phi +\theta t_{R}e+C}{1-(1-\theta )t_{N} (1+e\phi )-\theta t_{R}(1+e)-C} \end{aligned}$$

(47)

Finally, using the definitions of $\tau =(1-\theta )t_{N}+\theta t_{R}$, $\varepsilon =\frac{(1-\theta )t_{N}\phi +\theta t_{R}}{(1-\theta )t_{N}+\theta t_{R}}e$, (47) can be rearranged to (35), as required. $\square$

1.2 The VAT model

Model setup Consider a single industry with a fixed, large number of small traders producing a homogeneous good. Each small trader combines his own labor input l with an intermediate input x to produce output y via a fixed-coefficients technology

$$\begin{aligned} y=\min \left\{ l,\frac{x}{\gamma }\right\} , \end{aligned}$$

(48)

where $\gamma$ measures the input requirement per unit of output. In particular, for all traders, to produce one unit of output requires $\gamma$ units of input.

Individual traders are indexed by a skill or taste parameter $m\in [{\underline{m}},{\overline{m}}]$, assumed continuously distributed in the population with distribution $H(m(1-\gamma ))$ and density $h(m(1-\gamma ))$. A trader of type m has an overall payoff of

$$\begin{aligned} u(l;m)=\pi -\psi (l;m),\ \psi (l;m)=\frac{Am}{1+\frac{1}{e}}\left( \frac{l}{m}\right) ^{1+\frac{1}{e}} \end{aligned}$$

(49)

where $\pi$ is profit and $\psi (l;m)$ is the disutility of labor. So, traders are differentiated by disutility of labor.

For simplicity, it is assumed that traders only sell to final consumers, who have perfectly elastic demand for the good at price $p=1$. This is analogous to the assumption made in the taxable income literature that the wage is fixed, i.e., labor demand is perfectly elastic at a fixed wage. Finally, the intermediate input is produced only from labor supplied by non-trader households via a fixed-coefficients technology where one unit of labor is needed to produce one unit of the intermediate input. So, the tax-exclusive price of the output is w, the wage, which we also assume to be 1. This implies that the tax-exclusive value of sales is just y.

The traders and the producer of the intermediate input face a VAT system. It is assumed that the producer is VAT registered. If the trader is registered, he must charge VAT on sales y at rate t, but can claim back any VAT paid on inputs. The trader must register for VAT if the value of sales y exceeds the threshold $y_{0}$, but can register voluntarily even if $y<y_{0}$.

We can now compute trader profit as follows. When not registered, the price of the input is $1+t$. So, the profit for the non-registered trader is

$$\begin{aligned} \pi _{N}=(1-\gamma (1+t))y. \end{aligned}$$

(50)

where $\gamma$ is the cost of inputs relative to revenue per unit sold. For the registered trader, we reason as follows. This trader must charge VAT on his output. None of the output VAT can be passed on to the buyer, as he has perfectly elastic demand. So, revenue per unit sold is $p/(1+t)$. But, if the trader is registered, he can claim back VAT on the input use x, so the price of the input is $\gamma$. So, overall, the profit for the registered trader is

$$\begin{aligned} \pi _{R}=\left( \frac{1}{1+t}-\gamma \right) y. \end{aligned}$$

(51)

Trader payoffs and effective tax rates Trader utility is profit minus the disutility of labor. So, combining (38), (50), (51) and defining $n \equiv m(1-\gamma ),\ l=y,$ we get:

$$\begin{aligned} u_{N}&=(1-\gamma (1+t))y-\frac{A}{1-\gamma }\frac{n}{1+\frac{1}{e}}\left( \frac{y(1-\gamma )}{n}\right) ^{1+\frac{1}{e}}\\ u_{R}&=\left( \frac{1}{1+t}-\gamma \right) y-\frac{A}{1-\gamma }\frac{n}{1+\frac{1}{e}}\left( \frac{y(1-\gamma )}{n}\right) ^{1+\frac{1}{e} } \end{aligned}$$

(52)

Now, using $z=y(1-\gamma )$ in (52), and setting $A=1-\gamma$, we get

$$\begin{aligned} u_{N}&=\frac{1-\gamma (1+t)}{1-\gamma }z-\frac{n}{1+\frac{1}{e}}\left( \frac{z}{n}\right) ^{1+\frac{1}{e}} \\ u_{R}&=\left( \frac{1}{(1+t)(1-\gamma )}-\frac{\gamma }{1-\gamma }\right) z-\frac{n}{1+\frac{1}{e}}\left( \frac{z}{n}\right) ^{1+\frac{1}{e}} \end{aligned}$$

(53)

Finally, we note from (28) that

$$\begin{aligned} 1-t_{N}=\frac{1-\gamma (1+t)}{1-\gamma },\quad 1-t_{R}=\frac{1}{(1+t)(1-\gamma )}-\frac{\gamma }{1-\gamma } \end{aligned}$$

(54)

Then, combining (53), (54), we get (27), (28) as required.

Tax revenue Now we derive (29) in the text. Let y(n) be the sales of an n-type trader. Note that as m has distribution function $H(m(1-\gamma ))$, n has distribution function H(n). Then, revenue from the from the VAT is

$$\begin{aligned} R=\frac{t}{1+t}\int _{n_{R}}^{{\overline{n}}}y(n)h(n)\mathrm{d}n+t\int _{{\underline{n}} }^{n_{R}}\gamma y(n)h(n)\mathrm{d}n \end{aligned}$$

(55)

The first term is revenue from VAT levied on the value of sales of registered firms, because the sale price is $1/(1+t)$, and the second term is revenue from inputs sold by the intermediate input producer to firms that do not register for VAT. Using $z(n)=y(n)(1-\gamma )$, we can write this as

$$\begin{aligned} R=\frac{t}{(1+t)(1-\gamma )}\int _{n_{R}}^{{\overline{n}}}z(n)h(n)\mathrm{d}n+\frac{t\gamma }{1-\gamma }\int _{{\underline{n}}}^{n_{R}}z(n)h(n)\mathrm{d}n \end{aligned}$$

(56)

Finally, replacing z(n) by $z(1-t_{N};n),z_{0}$, or $z(1-t_{R};n)$ where appropriate, and using (54) for the definitions of $t_{N}, t_{R}$, we get (29) as required.