A collateral tax sanction: When does it mimic a welfare-improving tag?

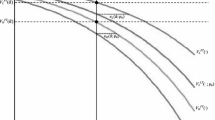
Abstract

The suspension of a driver’s license or the revocation of a passport or a professional license are used by the tax authorities as sanctions for failure to comply with tax obligations and are referred to as collateral tax sanctions. In this paper, I propose a new rationale for why it may be beneficial to use collateral tax sanctions for the purpose of tax enforcement. By affecting consumption and providing enforcement targeted to a group, collateral tax sanctions may allow the government to impose punishment correlated with an individual’s earning potential. Such punishment also makes the effective tax rates correlated with an individuals’ earning potential and therefore leads to a more effective redistribution of income. I show that the use of collateral tax sanctions could increase the CES social welfare function when the skill distribution of the targeted group first-order stochastically dominates the skill distribution of the other group and the social welfare function is sufficiently concave.

Appendices

Appendix

A Proofs

Proof of Proposition 1

The FOCs the determines the optimal evasion levels $E_{1}(I,t)$ and $E_{2}(I,t)$ are $t=\frac{\partial D_{1}(I,E_{1}^{*})}{\partial E}$ and $t=\frac{\partial D_{2}(I,E_{2}^{*})}{\partial E}$. Because $D_{i}(I,E)$ for $i=1,2$ strictly convex and $\frac{\partial D_{2}(I,E)}{\partial E}>\frac{\partial D_{1}(I,E)}{\partial E}$, these FOCs imply that $E_{1}^{*}>E_{2}^{*}$. Hence, $\eta _{2}-\eta _{1}=\frac{1}{I}(E_{1}^{*}-E_{2}^{*})>0$ and $\theta _{2}-\theta _{1}=\frac{1}{I}(E_{1}^{*}-E_{2}^{*})-\frac{1}{tI}(D_{1}(E_{1}^{*})-D_{2}(E_{2}^{*}))=\frac{1}{tI}[t(E_{1}^{*}-E_{2}^{*})-(D_{1}(E_{1}^{*})-D_{1}(E_{2}^{*})+D_{1}(E_{2}^{*})-D_{2}(E_{2}^{*}))]>$ $\frac{1}{tI}[t(E_{1}^{*}-E_{2}^{*})-\frac{\partial D_{1}(E_{1}^{*})}{\partial E}(E_{1}^{*}-E_{2}^{*})+(D_{2}(E_{2}^{*})-D_{1}(E_{2}^{*}))=\frac{1}{tI}[(D_{2}(E_{2}^{*})-D_{1}(E_{2}^{*})]>0$, where $D_{1}(E_{1}^{*})-D_{1}(E_{2}^{*})<\frac{\partial D_{1}(E_{1}^{*})}{\partial E}(E_{1}^{*}-E_{2}^{*})$ because $D_{1}(\cdot )$ is strictly convex in E, and $(D_{2}(E_{2}^{*})-D_{1}(E_{2}^{*})>0$ because $D_{i}(I,0)=0$ $i=1,2$, and $\frac{\partial D_{2}(I,E)}{\partial E}>\frac{\partial D_{1}(I,E)}{\partial E}$. $\square$

Proof of Lemma 1

Note first that from Eq. (9) it follows that utility function u(w) is strictly increasing on $[\underline{w},\overline{w}]$ because “information rent” is positive. That is, $\underset{w}{min}u(w)=u(\underline{w})$.

• (i) When $\rho$ converges to zero, the result is straightforward. Indeed,

  $$\begin{aligned} \underset{\rho =0}{lim}\beta (w)=\underset{\rho =0}{lim}\frac{u(w)^{-\rho }}{\int u(w)^{-\rho }f(w)\mathrm{d}w}=\frac{u(w)^{0}}{\int u(w)^{0}f(w)\mathrm{d}w}=\frac{1}{\int f(w)\mathrm{d}w}=1. \end{aligned}$$

• (ii) Consider $\rho$ converges to $\infty$. Define function $\gamma (w)=\frac{u(\underline{w})}{u(w)}$. Because $u(\underline{w})$ is strictly increasing on $[\underline{w},\overline{w}]$, function $\gamma (w)$ is strictly decreasing on $[\underline{w},\overline{w}]$ and $\gamma (\underline{w})=1$.

Consider $w=\underline{w}$. Then,

$$\begin{aligned} \underset{\rho =\infty }{lim}\beta (\underline{w})=\underset{\rho =\infty }{lim}\frac{\gamma (\underline{w})^{\rho }}{\int \gamma (s)^{\rho }f(s)\mathrm{d}s}=\underset{\rho =\infty }{lim}\frac{1}{\int \gamma (s)^{\rho }f(s)\mathrm{d}s}=\frac{1}{0}=\infty . \end{aligned}$$

Let me show that $\underset{\rho =\infty }{lim}\int \gamma (s)^{\rho }f(s)\mathrm{d}s=0$. By the definition of the limit, we need to show that $\forall \varepsilon >0$ $\exists \rho _{0}$ such that $\forall \rho \ge \rho _{0}$ $\int _{\underline{w}}^{\overline{w}}\gamma (s)^{\rho }f(s)\mathrm{d}s\le \varepsilon$. Indeed, define $f_{H}=\underset{w\in [\underline{w},\overline{w}]}{max}f(w)$. By the assumptions, $f_{H}$ is positive and bounded. For any given $\varepsilon >0$, define $\rho _{0}$ such that $\gamma (\underline{w}+\frac{\varepsilon }{2f_{H}})^{\rho _{0}}\le \frac{\varepsilon }{2}$. Such $\rho _{0}$ exists because $0<\gamma (\underline{w}+\frac{\varepsilon }{2f_{H}})<1$. Then, for $\forall \rho \ge \rho _{0}$ $\int _{\underline{w}}^{\overline{w}}\gamma (s)^{\rho }f(s)\mathrm{d}s=\int _{\underline{w}}^{\underline{w}+\frac{\varepsilon }{2f_{H}}}\gamma (s)^{\rho }f(s)\mathrm{d}s+\int _{\underline{w}+\frac{\varepsilon }{2f_{H}}}^{\overline{w}}\gamma (s)^{\rho }f(s)\mathrm{d}s\le \gamma (\underline{w})^{\rho }f_{H}\frac{\varepsilon }{2f_{H}}+\gamma (\underline{w}+\frac{\varepsilon }{2f_{H}})^{\rho }\int _{\underline{w}}^{\overline{w}}f(s)\mathrm{d}s=\frac{\varepsilon }{2}+\frac{\varepsilon }{2}=\varepsilon$.

Consider $w>\underline{w}$. Then, $\underset{\rho =\infty }{lim}\beta (w)=\underset{\rho =\infty }{lim}\frac{\gamma (w)^{\rho }}{\int \gamma (s)^{\rho }f(s)\mathrm{d}s}=\underset{\rho =\infty }{lim}\frac{1}{\int (\gamma (s)/\gamma (w))^{\rho }f(s)\mathrm{d}s}=\frac{1}{\infty }=0$. Let me now show that $\underset{\rho =\infty }{lim}\int _{\underline{w}}^{\overline{w}}(\gamma (s)/\gamma (w))^{\rho }f(s)\mathrm{d}s=\infty$. Indeed, $\underset{\rho =\infty }{lim}\int _{\underline{w}}^{\overline{w}}(\gamma (s)/\gamma (w))^{\rho }f(s)\mathrm{d}s=\underset{\rho =\infty }{lim}\int _{\underline{w}}^{w}(\gamma (s)/\gamma (w))^{\rho }f(s)\mathrm{d}s+\underset{\rho =\infty }{lim}\int _{w}^{\overline{w}}(\gamma (s)/\gamma (w))^{\rho }f(s)\mathrm{d}s=\infty +0=\infty$, where the second limit $\underset{\rho =\infty }{lim}\int _{w}^{\overline{w}}(\gamma (s)/\gamma (w))^{\rho }f(s)\mathrm{d}s$ converges to zero because for $s>w$ $\gamma (s)/\gamma (w)<1$ and the same consideration as in the previous case are applied. On the other hand, the first limit $\underset{\rho =\infty }{lim}\int _{\underline{w}}^{w}(\gamma (s)/\gamma (w))^{\rho }f(s)\mathrm{d}s$ converges to $\infty$ because for $\underline{w}\le s<w$ $\gamma (s)/\gamma (w)>1$. Let me show this formally by relying on the definition of the limit. Define $f_{L}=\underset{w\in [\underline{w},\overline{w}]}{min}f(w)$. By the assumptions, $f_{L}$ exists and is positive. For any given $\varepsilon >0$, define $\rho _{0}$ such that $(\gamma (\frac{\underline{w}+w}{2})/\gamma (w))^{\rho _{0}}f_{L}\frac{w-\underline{w}}{2}>\varepsilon$. Then, for $\forall \rho \ge \rho _{0}$ $\int _{\underline{w}}^{w}(\gamma (s)/\gamma (w))^{\rho }f(s)\mathrm{d}s>(\gamma ((w+\underline{w})/2)/\gamma (w))^{\rho }\int _{\underline{w}}^{(w+\underline{w})/2}f(s)\mathrm{d}s+\int _{(w+\underline{w})/2}^{w}f(s)\mathrm{d}s\ge (\gamma ((w+\underline{w})/2)/\gamma (w))^{\rho }f_{L}\frac{w-\underline{w}}{2}+f_{L}\frac{w-\underline{w}}{2}>\varepsilon$. $\square$

Proof of Lemma 2

The derivative of the social welfare function w.r.t. $\theta _{0}$ is

$$\begin{aligned} \begin{array}{l} \frac{\partial \mathrm{SWF}}{\partial \theta _{0}}=\left( \frac{\partial \mathrm{SWF}}{\partial t_{0}}-\frac{\partial \mathrm{SWF}}{\partial \eta _{0}}\frac{\eta _{0}}{t_{0}}\right) \frac{\eta _{0}}{\theta _{0}}+\frac{\partial \mathrm{SWF}}{\partial \eta _{0}}\frac{\partial \eta _{0}}{\partial \theta _{0}}=\frac{\partial \mathrm{SWF}}{\partial \eta _{0}}\left( \frac{\partial \eta _{0}}{\partial \theta _{0}}-\frac{\eta _{0}}{\theta _{0}}\right) \\ \quad =\int u_{1}(w)^{1-\rho }t\hat{I}f(w)\mathrm{d}w\left( \frac{\partial \eta _{0}}{\partial \theta _{0}}-\frac{\eta _{0}}{\theta _{0}}\right) , \end{array} \end{aligned}$$

where $\hat{I}=\int I(w)f(w)\mathrm{d}w$ is the average income. Thus, $\frac{\partial \mathrm{SWF}}{\partial \theta _{0}}$ is greater, equal or less than zero if $\frac{\partial \eta _{0}}{\partial \theta _{0}}$ is greater, equal or less than $\frac{\eta _{0}}{\theta _{0}}$. $\square$

Proof of Lemma 3

• (i) First, because distribution $F_{2}(w)$ first-order stochastically dominates distribution $F_{2}(w)$ and function $w^{1+\epsilon }$ is strictly increasing, it follows that $\hat{W}_{2}>\hat{W}_{1}$. Hence, $\widetilde{W}_{1}/\hat{W}_{1}-\widetilde{W}_{2}/\hat{W}_{2}>0$. Second, define $\rho _{0}=1+\frac{G_{0}}{\alpha _{0}\underline{w}_{1}}$, where $G_{0}=\eta _{0}t_{0}\left( \frac{1-\theta _{0}t_{0}}{1+1/\epsilon }\right) ^{\epsilon }\sum _{i=1,2}\int w^{1+\epsilon }\frac{f_{i}(w)}{2}\mathrm{d}w-R$ and $\alpha _{0}=\frac{1}{\epsilon }\left( \frac{1-\theta _{0}t_{0}}{1+1/\epsilon }\right) ^{1+\epsilon }$ then $\left. \beta _{i}(w)\right| _{\theta _{2}=\theta _{0}}=\frac{(\alpha _{0}w^{1+\epsilon }+G_{0})^{-\rho }}{\zeta }$, where $\zeta =\sum _{i=1,2}\int u_{i}(w)^{1-\rho }\frac{f_{i}(w)}{2}\mathrm{d}w$. Let me now show that if $\rho \ge \rho _{0}$ then $\beta (w)w^{1+\epsilon }$ is strictly decreasing function. Indeed, $\frac{\partial (\beta (w)w^{1+\epsilon })}{\partial w}=\frac{\partial }{\partial w}(\frac{\zeta w^{1+\epsilon }}{(\alpha _{0}w^{1+\epsilon }+G_{0})^{\rho }})=\frac{\zeta (1+\epsilon )w^{\epsilon }}{(\alpha _{0}w^{1+\epsilon }+G_{0})^{\rho +1}}(G_{0}-(\rho -1)\alpha _{0}w^{1+\epsilon })<0$ for $\rho \ge \rho _{0}$. Because distribution $F_{2}(w)$ first-order stochastically dominates distribution $F_{2}(w)$ and $\beta (w)w^{1+\epsilon }$ is strictly decreasing function, it follows that $-\widetilde{W}_{1}<-\widetilde{W}_{2}$ and $\hat{W}_{2}>\hat{W}_{1}$. Hence, $\widetilde{W}_{1}/\hat{W}_{1}>\widetilde{W}_{2}/\hat{W}_{1}>\widetilde{W}_{2}/\hat{W}_{2}$.

• (ii) According to Lemma 1, $\underset{\rho =\infty }{lim}\beta _{1}(w)={\left\{ \begin{array}{ll} \infty , &{} if\,w=\underline{w}_{1}\\ 0, &{} if\,w>\underline{w}_{1} \end{array}\right. }$ and $\underset{\rho =\infty }{lim}\beta _{2}(w)=0$ for $w\in [\underline{w}_{2},\overline{w}_{2}]$ because $\underline{w}_{1}=min\{\underline{w}_{1},\underline{w}_{2}\}$. Hence, $\widetilde{W}_{2}=0$ and $\widetilde{W}_{1}>0$. Therefore, $\widetilde{W}_{1}/\hat{W}_{1}-\widetilde{W}_{2}/\hat{W}_{2}>0$.$\square$

Proof of Lemma 4

• (i) According to (8), the FOCs are $1-\theta _{i}t=\frac{1}{\underline{w}_{i}}\varphi ^{'}(\frac{I_{i}(\underline{w}_{i})}{\underline{w}_{i}})$, for $i=1,2$. Because $\varphi$ is strictly convex and $(1-\theta _{2})\underline{w}_{2}>(1-\theta _{1})\underline{w}_{1}$, these FOCs imply $L_{2}(\underline{w}_{2})>L_{1}(\underline{w}_{1})$. Then, $u_{2}(\underline{w}_{2})-u_{1}(\underline{w}_{1})=I_{2}(\underline{w}_{2})(1-\theta _{2}t)-I_{1}(\underline{w}_{1})(1-\theta _{1}t)-[\varphi (L_{2}(\underline{w}_{2}))-\varphi (L_{1}(\underline{w}_{1}))]>$ $I_{2}(\underline{w}_{2})(1-\theta _{2}t)-I_{1}(\underline{w}_{1})(1-\theta _{1}t)-(1-\theta _{2}t)\underline{w}_{2}(\frac{I_{2}(\underline{w}_{2})}{\underline{w}_{2}}-\frac{I_{1}(\underline{w}_{1})}{\underline{w}_{1}})=((1-\theta _{2}t)\underline{w}_{2}-(1-\theta _{1})\underline{w}_{1})\frac{I_{1}(\underline{w}_{1})}{\underline{w}_{1}}>0$, where I have used that $\varphi (L_{2}(\underline{w}_{2}))-\varphi (L_{1}(\underline{w}_{1}))<\varphi ^{'}(L_{2}(\underline{w}_{2}))\left( L_{2}(\underline{w}_{2})-L_{1}(\underline{w}_{1})\right)$.

• (ii) If $(1-\theta _{2})\underline{w}_{2}>(1-\theta _{1})\underline{w}_{1}$, then according to part i) of this lemma $\underline{u}_{1}<\underline{u}_{2}$. Hence, according to Lemma 1, $\underset{\rho =\infty }{lim}\beta _{1}(w)={\left\{ \begin{array}{ll} \infty , &{} if\,w=\underline{w}_{1}\\ 0, &{} if\,w>\underline{w}_{1} \end{array}\right. }$ and $\underset{\rho =\infty }{lim}\beta _{2}(w)=0$ for $w\in [\underline{w}_{2},\overline{w}_{2}]$. Therefore, formula (22) reduces to (27). $\square$

Proof of Proposition 3

Note that formula (27) for $t_{0}$ when $\theta _{1}=\theta _{2}=\theta _{0}$ reduces to

$$\begin{aligned} \theta _{0}t_{0}=\frac{\eta _{o}(\hat{W}_{1}+\hat{W}_{2})-\theta _{o}\underline{W}_{1}}{(1+\epsilon )\eta _{o}(\hat{W}_{1}+\hat{W}_{2})-\theta _{o}\underline{W}_{1}}, \end{aligned}$$

(A.1)

where I used that $\int _{\underline{w}}^{\overline{w}}w^{1+\epsilon }f(w)\mathrm{d}w=\int _{\underline{w}}^{\overline{w}}w^{1+\epsilon }\frac{f_{1}(w)}{2}\mathrm{d}w+\int _{\underline{w}}^{\overline{w}}w^{1+\epsilon }\frac{f_{2}(w)}{2}\mathrm{d}w$.

To determine the sign of the change in the tax rate as a result of an increase in the effective tax factor, differentiate (27) w.r.t. $\theta _{2}$ and estimate the derivative $\frac{\partial t}{\partial \theta _{2}}$ at $\theta _{2}=\theta _{0}$ to get

$$\begin{aligned} \begin{array}{l} \left. \frac{\partial t}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}=\frac{t_{0}\hat{W}_{2}}{\theta _{0}(\hat{W}_{1}+\hat{W}_{2})}\left[ \frac{-(\frac{\eta _{0}}{\theta _{0}}(\hat{W}_{1}+\hat{W}_{2})-2\underline{W}_{1})-\theta _{0}t_{0}(1+\epsilon )\underline{W}_{1}}{(\frac{v_{0}}{\theta _{0}}(\hat{W}_{1}+\hat{W}_{2})-\underline{W}_{1})}\right] \\ \qquad \,\qquad \qquad -\frac{t_{0}\hat{W}_{2}}{\eta _{0}(\hat{W}_{1}+\hat{W}_{2})}\frac{(1-\theta _{0}t_{0})\theta _{0}\underline{W}_{1}}{(\eta _{0}(\hat{W}_{1}+\hat{W}_{2})-\theta _{0}\underline{W}_{1})}\left( \frac{\eta _{0}}{\theta _{0}}-\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}\right) , \end{array} \end{aligned}$$

(A.2)

where the last term in the above equation is negative because $\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}-\frac{\eta _{0}}{\theta _{0}}<0$.

For $\left. \frac{\partial t}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}$ to be negative, it is sufficient to have $\frac{\eta _{0}}{\theta _{0}}(\hat{W}_{1}+\hat{W}_{2})-2\underline{W}_{1}>0$.¹³ This implies that the average skill level should be sufficiently higher than the lowest skill level. If so, the optimal tax rate decreases with an increase in the effective tax factor, implying that tax revenue collected from taxpayers in group 1 decreases. The effective tax rate in group 2, however, increases, because $\left. \frac{\partial \theta _{2}t}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}=\frac{t_{0}}{\hat{W}_{1}+\hat{W}_{2}}\left( \hat{W}_{1}+\frac{\epsilon \theta _{0}t_{0}\hat{W}_{2}\underline{W}_{1}^{2}}{(\frac{\eta _{0}}{\theta _{0}}(\hat{W}_{1}+\hat{W}_{2})-\underline{W}_{1})^{2}}\right) -\frac{t_{0}\hat{W}_{2}}{(\hat{W}_{1}+\hat{W}_{2})}\frac{\epsilon \theta _{0}t_{0}\hat{W}\underline{W}_{1}}{(\frac{\eta _{0}}{\theta _{0}}(\hat{W}_{1}+\hat{W}_{2})-\underline{W}_{1})^{2}}\left( \frac{\eta _{0}}{\theta _{0}}-\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}\right)>\frac{t_{0}\hat{W}_{1}}{\hat{W}_{1}+\hat{W}_{2}}>0$ assuming that $\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}>\frac{\eta _{0}}{\theta _{0}}-\frac{min\{\underline{W}_{1},\underline{W}_{2}\}}{\hat{W}_{1}+\hat{W}_{2}}$.¹⁴ When the effective tax factor in group 2 increases, the lump-sum transfer also increases, because $\left. \frac{\partial G}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}=(1+\frac{1}{\epsilon })^{-\epsilon }(1-\theta _{0}t)^{\epsilon }(1-\epsilon \frac{\theta _{0}t_{0}}{1-\theta _{0}t_{0}})\frac{\epsilon \eta _{0}\theta _{0}\hat{W}_{2}\underline{W}_{1}^{2}}{(\eta _{0}(1+\epsilon )(\hat{W}_{1}+\hat{W}_{2})-\theta _{0}\underline{W}_{1})^{2}}>0$ presuming $\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}=\frac{_{0}}{\theta _{0}}$. This means that the increase in the taxes paid by taxpayers in group 2 outweighs the decrease in the taxes paid by taxpayers in group 1.

The expression for $\underline{u}_{i}(w)$ and for $u_{i}(w)$ for $i=1,2$ are now

$$\begin{aligned} \underline{u}_{i}= & {} \left( 1+\frac{1}{\epsilon }\right) ^{-\epsilon }\left( \eta _{1}t(1-\theta _{1}t)^{\epsilon }\hat{W}_{1}+\eta _{2}t(1-\theta _{2}t)^{\epsilon }\hat{W}_{2}\right. \nonumber \\&\qquad \qquad \qquad \qquad \left. +\frac{1}{1+\epsilon }(1-\theta _{i}t)^{1+\epsilon }\underline{w}_{i}^{1+\epsilon }\right) -R, \end{aligned}$$

(A.3)

$$\begin{aligned} u_{i}= & {} \underline{u}_{i}+\left( 1+\frac{1}{\epsilon }\right) ^{-\epsilon }\frac{1}{1+\epsilon }(1-\theta _{i}t)^{1+\epsilon }\left( w^{1+\epsilon }-\underline{w}_{i}^{1+\epsilon }\right) . \end{aligned}$$

(A.4)

By differentiating the above utilities w.r.t. $\theta _{2}$, we can determine how an increase in the effective tax factor in group 2 affects the utilities of individuals in each group. In doing this, remember that now $\frac{\partial \underline{u}_{1}}{\partial t}=0$, because t is chosen to maximize $\underline{u}_{1}$. The derivatives of the utilities w.r.t. $\theta _{2}$ are

$$\begin{aligned} \left. \frac{\partial \underline{u}_{1}}{\partial \theta _{2}}\right| _{\theta _{2}= \theta _{0}}= & {} \left( 1+\frac{1}{\epsilon }\right) ^{-\epsilon }t_{0}(1-\theta _{0}t_{0})^{\epsilon }\left[ \frac{\hat{W}_{2}\underline{W}_{1}}{\hat{W}_{1}+\hat{W}_{2}}-\hat{W}_{2}\left( \frac{\eta _{0}}{\theta _{0}}-\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}\right) \right] >0, \nonumber \\\end{aligned}$$

(A.5)

$$\begin{aligned} \left. \frac{\partial u_{1}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}= & {} \left. \frac{\partial \underline{u}_{1}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}+ \left( 1+\frac{1}{\epsilon }\right) ^{-\epsilon }(1-\theta _{0}t_{0})^{\epsilon }\theta _{0}\left( -\left. \frac{\partial t}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}\right) \nonumber \\&\quad \left( w^{1+\epsilon }-\underline{w}_{1}^{1+\epsilon }\right) >0, \end{aligned}$$

(A.6)

$$\begin{aligned} \left. \frac{\partial \underline{u}_{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}= & {} \left( 1+\frac{1}{\epsilon }\right) ^{-\epsilon }\frac{t_{0}(1-\theta _{0}t_{0})^{\epsilon }}{\hat{W}_{1}+\hat{W}_{2}}\left[ -\hat{W}_{1}\underline{W}_{2}\right. \nonumber \\&\left. -\frac{(1-\theta _{0}t_{0})\hat{W}_{2}\underline{W}_{1}^{2}(\underline{W}_{2}-\underline{W}_{1})}{\frac{\eta _{0}}{\theta _{0}}(\hat{W}_{1}+\hat{W}_{2})(\frac{\eta _{0}}{\theta _{0}}(\hat{W}_{1}+\hat{W}_{2})-\underline{W}_{1})}\right] \nonumber \\&-\left( 1+\frac{1}{\epsilon }\right) ^{-\epsilon }t_{0}(1-\theta _{0}t_{0})^{\epsilon }\hat{W}_{2}\left( \frac{\eta _{0}}{\theta _{0}}-\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}\right) <0, \end{aligned}$$

(A.7)

$$\begin{aligned} \left. \frac{\partial u_{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}= & {} \left. \frac{\partial \underline{u}_{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}+\left( 1+\frac{1}{\epsilon }\right) ^{-\epsilon }(1-\theta _{0}t_{0})^{\epsilon }\left( -\left. \frac{\partial \theta _{2}t}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}\right) \nonumber \\&\quad \left( w^{1+\epsilon }-\underline{w}_{2}^{1+\epsilon }\right) <0, \end{aligned}$$

(A.8)

where the estimate of the sign of $\left. \frac{\partial \underline{u}_{1}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}$ presuming that $\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}$ is not too small, specifically, that $\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}>\frac{\eta _{0}}{\theta _{0}}-\frac{min\{\underline{W}_{1},\underline{W}_{2}\}}{\hat{W}_{1}+\hat{W}_{2}}$.

These derivatives imply that everyone in group 2 receives a loss in their welfare and everyone in group 1 receives a gain in their welfare as a result of an increase in the effective tax factor in group 2. Because the Rawlsian social welfare function in this case is equal to $\underline{u}_{1}$, social welfare increases. $\square$

B Relaxation of the assumptions

I now relax the assumption that the gross effective tax factor and the net effective tax factor do not depend on the tax rate, that is, I now presume that $\theta (t)$ and $\eta (t)$. To separate the influence of the tax rate on $\theta$ and $\eta$ from the influence of the collateral tax sanction, I denote the collateral tax sanction by s. I assume that when the collateral tax sanction is imposed ($s>0$), we have $\frac{\partial \theta _{2}}{\partial s}>0$ ($\frac{\partial \eta _{2}}{\partial s}>0$) and $\frac{\partial \theta _{1}}{\partial s}=0$ ($\frac{\partial \eta _{1}}{\partial s}=0$).

First, note that the FOC describing the solution of the individual problem does not change, that is, $(1-\theta _{i}(t)t)=\frac{1}{w}\varphi ^{'}(\frac{I_{i}(w)}{w})$. However, the derivative of income w.r.t. the tax rate is now $\frac{\partial I_{i}}{\partial t}=-\frac{\theta _{i}+t\frac{\partial \theta _{i}}{\partial t}}{1-\theta _{i}t}\epsilon (w)I_{i}(w)$.

Second, under the assumption that the labor supply elasticity exhibits a constant wage elasticity ($\varphi (L)=L^{1+1/\epsilon }$, $\epsilon >0$), the FOC characterizing the optimal tax rate is now

$$\begin{aligned}&\frac{\left( \theta _{1}+t\frac{\partial \theta _{1}}{\partial t}\right) t}{1-\theta _{1}t}\epsilon \eta _{1}\left( \frac{1-\theta _{1}t}{1+1/\epsilon }\right) ^{\epsilon }\hat{W}_{1}+\frac{\left( \theta _{2}+t\frac{\partial \theta _{2}}{\partial t}\right) t}{1-\theta _{2}t}\epsilon \eta _{2}\left( \frac{1-\theta _{2}t}{1+1/\epsilon }\right) ^{\epsilon }\hat{W}_{2}\nonumber \\&\quad =\left( \frac{1-\theta _{1}t}{1+1/\epsilon }\right) ^{\epsilon }\left( \left( \eta _{1}+t\frac{\partial \eta _{1}}{\partial t}\right) \hat{W}_{1}-\left( \theta _{1}+t\frac{\partial \theta _{1}}{\partial t}\right) \widetilde{W}_{1}\right) \nonumber \\&\quad +\left( \frac{1-\theta _{2}t}{1+1/\epsilon }\right) ^{\epsilon }\left( \left( \eta _{2}+t\frac{\partial \eta _{2}}{\partial t}\right) \hat{W}_{2}-\left( \theta _{2}+t\frac{\partial \theta _{2}}{\partial t}\right) \widetilde{W}_{2}\right) , \end{aligned}$$

(A.9)

and Eq. (23) determining $t_{0}$ is now

$$\begin{aligned} \frac{\left( \theta _{0}+t\frac{\partial \theta _{0}}{\partial t}\right) t_{0}}{1-\theta _{0}t_{0}}=\frac{\left( \eta _{0}+t\frac{\partial \eta _{0}}{\partial t}\right) \hat{W}-\left( \theta _{0}+t\frac{\partial \theta _{0}}{\partial t}\right) \widetilde{W}}{\epsilon \eta _{0}\hat{W}}, \end{aligned}$$

(A.10)

where $\hat{W}_{i}=\int w^{1+\epsilon }\frac{f_{i}(w)}{2}\mathrm{d}w$, $\widetilde{W}_{i}=\int \beta _{i}(w)w^{1+\epsilon }\frac{f_{i}(w)}{2}\mathrm{d}w$, $\hat{W}=\int w^{1+\epsilon }f(w)\mathrm{d}w=\hat{W}_{1}+\hat{W}_{2}$, and $\widetilde{W}=\int \beta (w)w^{1+\epsilon }f(w)\mathrm{d}w=\widetilde{W}_{1}+\widetilde{W}_{2}$.

Finally, the derivative of (24) w.r.t. s can be expressed as:

$$\begin{aligned} \left. \frac{\partial \mathrm{SWF}}{\partial s}\right| _{\theta _{2}=\theta _{0}}= & {} \frac{\partial \theta _{2}}{\partial s}t\left( \frac{1-\theta _{0}t}{1+1/\epsilon }\right) \hat{W}_{2} \left[ \left. \left( \frac{\widetilde{W}}{\hat{W}}-\frac{\widetilde{W}_{2}}{\hat{W}_{2}}\right) \right| _{\theta _{2}=\theta _{0}}\right. \nonumber \\&\left. +\left( \left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}-\frac{\eta _{0}+t\frac{\partial \eta _{0}}{\partial t}}{\theta _{0}++t\frac{\partial \theta _{0}}{\partial t}}\right) \right] . \end{aligned}$$

(A.11)

This equation is analogous to Eq. (25) and leads to the following condition for the collateral tax sanction to be socially beneficial:

$$\begin{aligned} \left. \left( \frac{\widetilde{W}}{\hat{W}}-\frac{\widetilde{W}_{2}}{\hat{W}_{2}}\right) \right| _{\theta _{2}=\theta _{0}}>\frac{\eta _{0}+t\frac{\partial \eta _{0}}{\partial t}}{\theta _{0}++t\frac{\partial \theta _{0}}{\partial t}}-\left. \frac{\partial \eta _{2}}{\partial \theta _{2}}\right| _{\theta _{2}=\theta _{0}}. \end{aligned}$$

(A.12)

Thus, the use of the collateral tax sanction could improve social welfare when the social welfare function is sufficiently concave and the skill distribution in group 2 first-order stochastically dominates the skill distribution in group 1.