Three-dimensional Quantum Slit Diffraction and Diffraction in Time

Abstract

We derive a self-consistent formula for the quantum propagator of the quantum diffraction by a reflecting (or non-absorbing) screen with an arbitrary aperture, in the transmission region. To achieve this, we use the Green function approach (Brukner and Zeilinger, Phys. Rev. A. 56(5), 3804–3824 1997) that we extend to mixed boundary conditions (including Dirichlet and Neumann) on the shutter’s screen and to any initial wave functions, such as Gaussian wave packets. To illustrate our results, we apply this method to the famous rectangular slit diffraction problem. It allows us to take into account the effect of the quantum nature of the motion perpendicular to the screen where the diffraction-in-time phenomenon appears in this direction. Then we derive corrections to the standard semi-classical formula and the diffraction pattern. We also point out situations in which this might be observable. In particular, we discuss the diffraction in space and time in the presence of gravity.

Appendices

Appendix 1: The Truncation Approximation for the Quantum-Multi-Slit Diffraction Problem

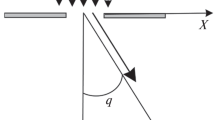
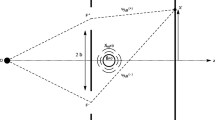
We recall [14] that the single “gate” slit propagator, centered on the x-axis of size 2a on the z-axis and 2b on the y-axis is given by the following formula [14]:

$$\begin{array}{@{}rcl@{}} &&K_{\text{Trunc}}^{(a,b)}(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1},t_{c})=\\ &&{\kern15pt} \frac{e^{i\frac{m(x-x_{0})^{2}}{2\hbar t}}}{(2i\pi\hbar t/m)^{1/2}} {\int}_{-a}^{a}dz_{1} {\int}_{-b}^{b}dy_{1} \frac{e^{i\frac{m[(y-y_{1})^{2}+(z-z_{1})^{2}]}{2\hbar(t-t_{c})}}}{2i\pi\hbar(t-t_{c})/m} \frac{e^{i\frac{m[(y_{1}-y_{0})^{2}+(z_{1}-z_{0})^{2}]}{2\hbar t_{c}}}}{2i\pi\hbar t_{c}/m}\ , \end{array} $$

(70)

where t _c =|x ₁−x ₀|t/|x−x ₀|. We note that this formula is valid only if the distances on the x-axis are very large compared to the distance on the screen and to the sizes of the slit, i.e. for |x−x ₁|,|x ₁−x ₀|≫a,b,|y|,|z|. The formula (70) can be interpreted as follows: The propagator is the sum over the paths x(τ) of the particle going from the source (x(0)=x ₀,z(0)=z ₀,y(0)=y ₀) to the screen (x(t)=x,z(t)=z,y(t)=y), given that it goes through the slit x(t _c )=x ₁, z(t _c )=z ₁∈[−a,a], y(t _c )=y ₁∈[−b,b] at the time t _c defined just above. Notice that we can find an explicit formula for the propagator (70) in terms of the Fresnel function [12], [14]:

$$ K_{\text{Trunc}}^{(a,b)}(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1},t_{c})= \frac{e^{im\frac{|\mathrm{r}-\mathrm{r}_{0}|^{2}}{2\hbar t}}}{(2i\pi\hbar t/m)^{3/2}} F_{t,t_{c}}(z,a)F_{t,t_{c}}(y,b) $$

(71)

where:

$$ F_{t,t_{c}}(z,a)\equiv \left(C[\alpha_{t,t_{c}}(z,a)]+C[\alpha_{t,t_{c}}(z,-a)]+iS[\alpha_{t,t_{c}}(z,a)]+iS[\alpha_{t,t_{c}}(z,-a)]\right) $$

(72)

and where the Fresnel functions are defined as follows [32]: $C[u]={{\int }_{0}^{u}}dw\ \cos {(\frac {\pi w^{2}}{2})}$, and $S[u]={{\int }_{0}^{u}}dw\ \sin {(\frac {\pi w^{2}}{2})}$. Since we have seen that $\lambda \approx 2\pi \hbar /mv_{x}$ with v _x =|x−x ₀|/t and t _c ≈|x ₁−x ₀|/v _x =|x ₁−x ₀|t/|x−x ₀|, the function $\alpha _{t,t_{c}}(z,a)$ in (72) can be written as follows :

$$ \alpha_{t,t_{c}}(z,a)\equiv \sqrt{\gamma N_{F}}\left(1-\frac{z}{a\gamma}\right)\ , $$

(73)

where γ=|x−x ₀|/|x ₁−x ₀| and where the Fresnel number is defined as N _F ≡2a ²/(λ L), where L=|x−x ₁|.

For a narrow Gaussian wave packet (i.e., in the limit σ→0), the intensity on the screen is proportional to the modulus square of the propagator, and is given by[14]:

$$ I_{\text{Trunc}}^{(a,b)}(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1},t_{c})| =I_{0}\left(\frac{m}{2\pi\hbar t}\right)^{3}|F_{t,t_{c}}(z,a)|^{2}|F_{t,t_{c}}(y,b)|^{2} $$

(74)

In [14] three distinct regimes were considered depending on the value of the Fresnel number:

• (i) If N _F ≪1: we have the Fraunhofer regime, which means that the distances are sufficiently large to get a usual interference pattern [33] where the distance between two consecutive minima of intensity are about λ L/(2a) in the z-direction and λ L/(2b) in the y-direction.

• (ii) If N _F ≫1: we are in the so-called Fresnel regime where the interference pattern has a similar shape as the gate but with a different scale: a(γ−1) in the z-direction and b(γ−1) in the y-direction. More specifically, the intensity is very small if z>a(γ−1) and y>b(γ−1) and oscillate very fast around a constant if z<a(γ−1) and y<b(γ−1).

• (iii) If N _F ∼1: the intermediate regime is a transition between both regimes for which there is a spreading around the center of the intensity and similar to the Fraunhofer regime for large distances (on the screen).

The formula for the multi-slit problem is given by the sum over the single-slit propagator for each slit (centered in (A _j ,B _j ), j=1,..,N) and then to get the interference pattern on the screen, we have to compute the square modulus of the N-slit propagator.

Appendix 2: Derivation of the Point-Source Propagator

By (17), the point-source propagator is given by

$$\begin{array}{@{}rcl@{}} K(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1})&\equiv& {{\int}_{0}^{t}} d\tau\left[\frac{-x_{0}}{\tau}\eta_{1}+\frac{x}{t-\tau}\eta_{2}\right]G_{0}(\mathrm{r}-\mathrm{r}_{1},t-\tau)G_{0}(\mathrm{r}_{1}-\mathrm{r}_{0},\tau) \end{array} $$

(75)

$$\begin{array}{@{}rcl@{}} =\eta_{2}K^{(D)}(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1}) +\eta_{1}K^{(N)}(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1}) \end{array} $$

(76)

where we have introduced the Dirichlet part:

$$\begin{array}{@{}rcl@{}} K^{(D)}(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1}) ={{\int}_{0}^{t}} d\tau\left[\frac{x}{t-\tau}\right]G_{0}(\mathrm{r}-\mathrm{r}_{1},t-\tau)G_{0}(\mathrm{r}_{1}-\mathrm{r}_{0},\tau) \end{array} $$

(77)

and the Neumann part:

$$\begin{array}{@{}rcl@{}} K^{(N)}(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1}) ={{\int}_{0}^{t}} d\tau\left[\frac{-x_{0}}{\tau}\right]G_{0}(\mathrm{r}-\mathrm{r}_{1},t-\tau)G_{0}(\mathrm{r}_{1}-\mathrm{r}_{0},\tau) \end{array} $$

(78)

We will use the Laplace transform defined by

$$\begin{array}{@{}rcl@{}} LT\left[f(\tau);\tau,s\right]={\int}_{0}^{+\infty}d\tau\ e^{-s\tau}f(\tau) \end{array} $$

and the inverse Laplace transform

$$\begin{array}{@{}rcl@{}} LT^{-1}\left[F(s);s,\tau\right]={\int}_{c-i\infty}^{c+i\infty}\frac{ds}{2i\pi}\ e^{\tau s}F(s), \end{array} $$

where c is a real-valued constant chosen such that the integral remains finite. We have the following Laplace transforms (see equations (28) P.147 §4.5 and (5) P.246 §5.6 in [34]):

$$\begin{array}{@{}rcl@{}} LT\left[\left(\frac{m}{2i\pi\hbar t}\right)^{3/2}e^{i\frac{m|\mathrm{r}|^{2}}{2\hbar t}};t,s\right]= \frac{e^{i|\mathrm{r}|\sqrt{2mis/\hbar}}}{2i\pi\hbar|\mathrm{r}|/m} \end{array} $$

(79)

$$\begin{array}{@{}rcl@{}} LT\left[\frac{1}{t}\left(\frac{m}{2i\pi\hbar t}\right)^{3/2}e^{i\frac{m|\mathrm{r}|^{2}}{2\hbar t}};t,s\right]= \frac{e^{i|\mathrm{r}|\sqrt{2mis/\hbar}}}{2i\pi|\mathrm{r}|^{2}}\left(-\sqrt{2mis/\hbar}+\frac{i}{|\mathrm{r}|}\right) \end{array} $$

(80)

So by (78) and (79) we get

$$\begin{array}{@{}rcl@{}} &&K^{(N)}(\mathrm{r},t;\mathrm{r}_{0},0|\mathrm{r}_{1})\\ &=&\frac{-m x_{0}}{\hbar}\times LT^{-1} \left[\frac{e^{i|\mathrm{r}-\mathrm{r}_{1}|\sqrt{2m i s/\hbar}}}{2i\pi|\mathrm{r}-\mathrm{r}_{1}|} \frac{e^{i|\mathrm{r}_{1}-\mathrm{r}_{0}|\sqrt{2m i s/\hbar}}}{2i\pi|\mathrm{r}_{1}-\mathrm{r}_{0}|^{2}} \left(-\sqrt{2mis/\hbar}+\frac{i}{|\mathrm{r}_{1}-\mathrm{r}_{0}|}\right);s,t\right] \end{array} $$

(81)

then using the inversion formulas (79), we get (18) where the amplitude is given by (21) and the phase by (19).

Similary for the Dirichlet boundary condition, by the symmetries t ₁⇔t−t ₁ and u ₁⇔u ₂ in (81), we get that the amplitude is given by (22) and that the phase does not change and is given by (19).