Abstract
Absolute spectral radiometry is currently the only established primary thermometric method for the temperature range above 1300 K. Up to now, the ongoing improvements of high-temperature fixed points and their formal implementation into an improved temperature scale with the mise en pratique for the definition of the kelvin, rely solely on single-wavelength absolute radiometry traceable to the cryogenic radiometer. Two alternative primary thermometric methods, yielding comparable or possibly even smaller uncertainties, have been proposed in the literature. They use ratios of irradiances to determine the thermodynamic temperature traceable to blackbody radiation and synchrotron radiation. At PTB, a project has been established in cooperation with VNIIOFI to use, for the first time, all three methods simultaneously for the determination of the phase transition temperatures of high-temperature fixed points. For this, a dedicated four-wavelengths ratio filter radiometer was developed. With all three thermometric methods performed independently and in parallel, we aim to compare the potential and practical limitations of all three methods, disclose possibly undetected systematic effects of each method and thereby confirm or improve the previous measurements traceable to the cryogenic radiometer. This will give further and independent confidence in the thermodynamic temperature determination of the high-temperature fixed point’s phase transitions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Absolute spectral radiometry is at present the only reliable primary thermometric method for the temperature range above 1300 K [1]. The currently ongoing improvements to the high-temperature range of the ITS-90, i.e., the development of novel high-temperature fixed points (HTFP) and their formal implementation into an improved temperature scale with the mise en pratique for the definition of the kelvin, rely solely on thermodynamic temperature measurements based on single-wavelength absolute radiometry traceable to the cryogenic radiometer (CR) [2]. The wording “single-wavelength” for a narrow band filter radiometer is used to distinguish from “double-wavelength method”. The filter radiometers are calibrated at a sufficient number of wavelength points over their whole bandpass.
Two alternative primary thermometric methods, yielding comparable or even smaller uncertainties in thermodynamic temperature measurement, have been proposed in the literature [3, 4] but have so far not been applied to the measurement of the phase transition temperatures of HTFPs. These methods use ratios of irradiances to determine the thermodynamic temperature of HTFPs traceable to blackbody radiation (BB) and synchrotron radiation (SR).
Alternative I is the “double-wavelength method” [3]. With this method, the spectral irradiances of two BBs of different temperatures are measured with two filter radiometers (FR) of different central wavelengths. The FRs are calibrated only for their relative spectral responsivity. Based on these four measurements, the thermodynamic temperatures of the two BBs are calculated according to Planck’s law. An error function of ratios must be minimized.
Alternative II is the “blackbody-versus-synchrotron method” [4]. With this method, the spectral irradiance at the electron storage ring of PTB, the Metrology Light Source (MLS) [5], will be measured and calculated according to Schwinger’s theory. Two FRs of different central wavelengths which are calibrated only for their relative spectral responsivity are used. With the same two FRs, a BB with a large-area HTFP is measured and the thermodynamic temperature is calculated according to Planck’s law. The thermodynamic temperature is determined by fitting the ratios of measured and calculated irradiance ratios from SR and BB.
We are going to use all three methods—absolute radiometry (traceable to CR) and both alternative methods (traceable to BB and SR)—simultaneously for the temperature measurement of HTFPs. For this, a four-wavelengths ratio filter radiometer (FRFR) was developed, as a dedicated instrument for absolute thermodynamic temperature measurement. With the FRFR, four filter radiometers with their center wavelengths in the VIS and NIR spectral range are combined into a single instrument with one common aperture. With these three independent methods performed in parallel on HTFPs, we aim to compare the potential and practical limitations of all three methods, disclose possibly undetected systematic effects of each method and thereby confirm or improve the previous measurements traceable to the CR. This will give further and independent confidence in the thermodynamic temperature determination of the HTFP phase transitions.
2 Radiometric Methods for Thermodynamic Temperature Measurement
In the following, we give a short summary of the three radiometric methods we intend to apply with the FRFR for the thermodynamic temperature measurement of HTFPs phase transition temperatures.
2.1 Single-Wavelength Absolute Radiometry
The established method for primary high-temperature measurements is single-wavelength absolute radiometry. It is based on the measurement of the thermodynamic temperature of a BB with a single FR of known absolute spectral responsivity. An FR, typically, consists of a precision aperture, a narrow bandwidth interference filter and a photodiode. These components are enclosed in a temperature-stabilized housing. Figure 1 shows the typical setup for absolute radiometry measurements in the irradiance mode. An additional temperature-stabilized precision aperture is placed in front of the BB to define its radiating area. Both apertures are circular with known radii \(r_{1}\) and \(r_{2}\) and aligned in parallel and coaxial with a known distance d between them.
The spectral responsivity of the FR is traceable to the CR via a trap detector [1, 6, 7]. The photocurrent measured by the FR is given by the integral:
The geometric factor G is defined as:
The symbol \(\varepsilon \) ( \(\lambda \)) represents the effective emissivity of the blackbody cavity, and \(s_{E}(\lambda )\) is the spectral irradiance responsivity. The spectral radiance \(L_{{\lambda }}\) is determined according to Planck’s law:
Where h is Planck’s constant, \(k_{B}\) is Boltzmann’s constant, n is the index of refraction of the medium, \(c_{0}\) is the speed of light in vacuum, and T is the temperature inside the BB. The thermodynamic temperature T is determined by iterative numerical integration of Eq. 1.
Single-wavelength absolute radiometry has been successfully and extensively used over the last two decades to measure the temperature of the phase transitions of HTFPs. Recent results on Re-C cells are for example given in [2].
In Fig. 2 the typical uncertainty components of single-wavelength absolute radiometry are presented. The major source of uncertainty for spectral irradiance measurement is the size of the aperture in front of the BB.
The following ratio methods avoid uncertainties that originate from geometrical quantities.
2.2 Two-Wavelengths Ratio Radiometry
The first presented alternative, the “double-wavelength method”, goes back to Wulfson [3]. It is solely based on blackbody radiation according to Planck’s law. Two FRs with known relative spectral irradiance responsivity ŝ \(_{E,{\lambda }}\) measure two temperatures [8, 9]. Relative spectral irradiance responsivities ŝ \(_{E,{\lambda } }\)can be determined with lower uncertainties than absolute spectral irradiance responsivities \(s_{E,{\lambda }}\). The scaling factors a and b between them need not to be known.
Both thermodynamic temperatures \(T_{1}\) and \(T_{2}\) can be found by minimizing an error function \(E_{12}\) of measured ratios of photocurrents and of calculated ratios.
In the calculated ratios, the scale factors and the geometric factor cancel out:
As BBs, we are going to use HTFPs operated in a variable temperature high-temperature blackbody (HTBB). The reason for this is that HTFPs show highly reproducible phase transition temperatures and are very stable.
The second alternative is the “blackbody-versus-synchrotron method”. It has been proposed by Sapritsky and published together with Madden et al [4]. Two FRs with known relative spectral irradiance responsivity \({\hat{s}}_{E,{\lambda }}\), measure SR of known spectral irradiance \(E_{{\lambda }}\). The transmission of the window \(\tau \) is an important issue. The transmission is measured by comparing signals with/without the window in a wavelength range from 400 nm to 1800 nm with Si and InGaAs detectors. The spectral comparator facility we used for this is a combination of a prism monochromator and a grating monochromator. It is a well-established method at PTB.
Also in this ratio method, the scaling factors and the geometric factor cancel out. This equation can be solved using numerical techniques to obtain the temperature of the BB.
With this ratio method, we are going to use the MLS [10] of the PTB, which is operated as a primary source standard. The MLS is equipped with a dedicated white light beamline. This beamline provides calculable SR according to Schwinger’s theory [11]. The electron energy can be set to values from 105 MeV to 630 MeV. The electron beam current can be varied from 1 pA to 200 mA.
In an electron storage ring accelerated electrons with relativistic velocities in bending magnets emit radiation in tangential directions. The most important ring parameters are the electron energy \(E_{e,}\) electron current \(I_{e}\), magnetic induction B, vertical emission angle \(\psi \) and effective vertical source size \(\Sigma _{y}\).
The spectrum of emitted radiation is very broad and reaches from the vacuum ultraviolet (VUV) to the near-infrared (NIR) spectral range. Figure 3 shows the spectral irradiance \(E_{{\lambda }}\) of the MLS in the VIS and NIR spectral range in comparison to a BB at 3000 K for the geometrical parameters used in the experiments, respectively. Depending on the wavelength, the spectral irradiances \(E_{{\lambda }}\) of the MLS and of the BB differ from each other. The larger the wavelength, the wider the difference of both irradiances. However, the levels of ratios of spectral irradiances at the MLS and the levels of ratios at the BB are comparable for the given geometry and used FR wavelengths. The center wavelengths of the four FRs of the FRFR are plotted in Fig. 3.
Spectral irradiance of the electron storage ring MLS and of a BB as functions of wavelength \(\lambda \). The circular aperture stop used in each case has a diameter of 3 mm. MLS: electron energy \(E_e = 630\) MeV, electron current \(I_e\) = 100 mA, magnetic induction \(B = 3.8\) T, distance between tangent point and aperture of FR \(d = 22\) m. BB: temperature \(T = 3000\) K, circular aperture of diameter 20 mm and a distance between apertures of \(d = 1\) m
The angular distribution of the spectral irradiance is homogeneous in the horizontal direction. It has a narrow angular distribution in the vertical direction, which is wavelength dependent. Because of this, the mean value of the spectral irradiance \(E_{{\lambda },SR}\) within the angular acceptance must be considered in Eq. 9. Furthermore, SR shows a linear polarization of the radiation in the orbital plane of the electrons and an elliptical polarization above and below the orbital plane. Because of that the FRs have to be measured in two orientations which are perpendicular to each other.
3 The Four-Wavelengths Ratio Filter Radiometer (FRFR)
All three primary standards—cryogenic radiometer, blackbody and electron storage ring—are available at PTB. Figure 4 shows the flow diagram of calibration chain. For absolute method, the cryogenic radiometer is used as a primary standard—for ratio methods as a grey detector. In Fig. 5, we give a schematic view of how we will apply these primary standards with the above-described three primary thermometric methods to determine the phase transition temperature of HTFPs.
To apply the three primary standards with the three methods simultaneously, we have designed and built a dedicated instrument, the FRFR. Figure 3 shows the center wavelengths of the four FRs in the VIS and NIR wavelength region which are the central part of the FRFR. Some characteristics of the four FRs are given in Table 1. A schematic drawing and a photography of the FRFR are given in Fig. 6a, b.
The FRFR consists of four FRs with one common aperture and one common amplifier. The four FRs are linearly movable behind the aperture by a computer-controlled translation stage with a repeatability of ± 2.5 \(\mu \)m. The aperture and the four FRs are temperature stabilized. The instrument is a portable system, which can travel between the different primary standards without losing its calibration.
Using one common aperture is a key point of the FRFR. Figures 7 and 8 show the high-precision knife-edge aperture as a drawing and a microscopic picture of its edge. It is made of a tungsten carbide/cobalt composite material.
Figure 9 is a schematic diagram of the planned measurement scheme with the FRFR at the MLS. The white light beamline of the MLS has a stray light aperture and ends with a window of fused silica. The window has been tilted to minimize interreflections between the window and the aperture and/or the interference filters of the FRFR. The distance from the source point of the storage ring to the FRFR aperture is approx. 22 m.
The HTFPs are operated in a variable temperature HTBB. The distance between the radiation aperture of the HTBB and the FRFR aperture is approx. 1 m.
4 Preliminary Results
4.1 SR Measurements
At the white light beamline of the MLS, first test measurements were performed with two of the four previously mentioned FRs at wavelengths 650 nm and 1550 nm. As the FRFR was still under construction when these measurements were carried out, the two FRs were applied as single individual FRs not included in the FRFR. Figure 10 shows a single FR with its axis for translation and rotation. The FR and the tilted window are in a light-tight box. The aim was to determine the best orientation of the FRs with best reduction in interreflections. Also analyzed were stability of photocurrent and the possibility of stray light reduction.
Figure 11a shows that a horizontal scan (X axis in Fig. 10) gives a homogeneous detector signal with the FR in the SR. It differs slightly with different heights over the orbital plane of the storage ring. Figure 11b shows that the vertical scan (Y axis in Fig. 10) behaves as predicted in Schwinger’s theory, with a minimum of signal in the orbital plane.
The tilted window strongly reduced the interreflections. Figure 12a, b shows the results of rotational scans around X and Y axis of the FR. However, there are still some interreflections. This is especially the case when the tilted window and the FRs are aligned in parallel. Therefore, this rotation angle around X axis must be avoided.
In addition, we measured the SR signal in two orientations of the FR: 0\({^{\circ }}\) and 90\({^{\circ }}\) (rotation around the Z axis in Fig. 10) to study the polarization effects. Finally, we investigated the stability of the photocurrent. Figure 13 shows that the relative stability of the photocurrent is within a 2.5\(\times \)10\(^{-4}\) region at typical photocurrents of a few nA.
We also investigated stray light and diffraction. Stray light is caused by diffuse reflections on the inner wall of the beamline. It can be reduced by contracting the four knife-edges thus reducing the size of the stray light aperture. Figure 14a shows as a result the constrained spot on the front of the FR.
Yet similarly, diffraction due to the knife-edges of the stray light aperture appears like Figs. 14b and 15 show at top and bottom as well as left and right edges of the spot. They are wavelength dependent and affect the signal more at longer wavelengths.
A trade-off between stray light reduction and diffraction has to be found. In addition, we can detect influence of installed diagnostic instruments.
First results are very promising in terms of stability and reproducibility. Nevertheless, the most crucial part will be the mitigation of interreflections as well as stray light and diffraction contributions.
4.2 HTFP Development
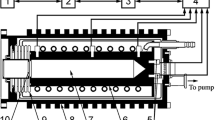
VNIIOFI developed and characterized large-aperture HTFP cells of Re-C and WC-C [12]. Figure 16 shows the large-aperture cell with diameter of 14 mm and a length of 60 mm as well as the small-aperture HTFP with diameter of 3 mm and a length of 44 mm. The furnace for the large cell is a HTBB of type BB3500MP with a pyrolytic graphite cavity with a diameter of 57 mm [13]. The large aperture of the cell allows measurements in irradiance mode.
We compared phase transitions of the large-aperture and small-aperture HTFPs with the setup of Fig. 17. A temperature difference of about 0.5 K was detected [13]. The difference can be caused by lower effective emissivity or/and by “temperature drop” effect due to higher radiation loses of the large cell. After further experiments, the reasons will be better understood and then the corrections will be applied. Development of the large-area cell will be continued to reduce the temperature difference with the small one as much as possible.
5 Summary and Outlook
Three primary thermometric methods applying all three primary radiometric standards—cryogenic radiometer, blackbody radiator and electron storage ring—are discussed for the determination of the phase transition temperatures of HTFPs. A dedicated instrument, the FRFR, has been developed to apply all three methods with one instrument at the primary standards of PTB.
Single-wavelength absolute radiometry shows very good results and is well established. However, so far all primary measurements on HTFPs have been solely performed by this method. Additionally, it has a large geometric uncertainty contribution.
Two alternatives have been proposed to overcome this by using ratios of irradiances. With these methods, the geometry cancels out. They are traceable to blackbody radiation only or to blackbody radiation and synchrotron radiation. These alternatives are possible because of newly developed large-aperture HTFPs. They allow irradiance mode measurements. Thereby, uncertainty contributions are reduced by the absence of optical systems between source and detector.
A dedicated instrument—the FRFR—has been designed and constructed. It is going to use all three methods simultaneously and will apply all three primary radiometric standards. It consists of four filter radiometers with one common aperture.
First measurements for the determination of the alignment, temperature stability and stray light reduction were carried out with single filter radiometers at the synchrotron radiation source of PTB—the Metrology Light Source. VNIIOFI developed and characterized large-aperture HTFPs of Re-C and WC-C.
We aim to compare the potential and practical limitations of all three methods in the near future.
References
J. Hartmann, J. Hollandt, P. Meindl, R.D. Taubert, L. Werner, MAPAN J. Metrol. Soc. India 25, 3–10 (2010)
E.R. Woolliams et al., Philos. Trans. R. Soc. A 374, 20150044 (2016)
K.S. Wulfson, J. Exp. Theor. Phys. 21, 507–509 (1951). [in Russian]
R.P. Madden, T.R. O’Brian, A.C. Parr, R.D. Saunders, V. Sapritsky, Metrologia 32, 425–429 (1995/96)
R. Klein, R.D. Taubert, R. Thornagel, J. Hollandt, G. Ulm, Metrologia 46, 359–366 (2009)
N. Fox, Metrologia 32, 535–543 (1995/96)
R.D. Taubert, R. Friedrich, J. Hartmann, J. Hollandt, Metrologia 40, 35–38 (2003)
E.R. Woolliams, R. Winkler, S.G.R. Salim, P.M. Harris, I.M. Smith, Int. J. Thermophys. 30, 144–154 (2009)
P. Saunders, Int. J. Thermophys. 35, 417–437 (2014)
R. Klein, B. Brandt, R. Fliegauf, A. Hoehl, R. Müller, R. Thornagel, G. Ulm, Metrologia 46, S266–S271 (2009)
J. Schwinger, Phys. Rev. 75, 1912–1925 (1949)
B. Khlevnoy, I. Grigoryeva, V. Sapritsky, K. Anhalt , M. Wähmer, TEMPMEKO 2016, in 13th International Symposium on Temperature and Thermal Measurements in Industry and Science, Zakopane/Poland
S.A. Ogarev, B.B. Khlevnoy, M.L. Samoylov, V.I. Shapoval , V.I. Sapritsky, in Proceedings of TEMPMEKO 2004, ed. by L.G. Bermanec, T. Stasic, T. Veliki, Covtat-Dubrovnik (2004), pp. 569–574
Acknowledgements
This work partly funded by the EMPIR project “Implementing the new kelvin 2”. The EMPIR is jointly funded by the EMPIR participating countries within EURAMET and the European Union.
Author information
Authors and Affiliations
Corresponding author
Additional information
Selected Papers of the 13th International Symposium on Temperature, Humidity, Moisture and Thermal Measurements in Industry and Science.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wähmer, M., Anhalt, K., Hollandt, J. et al. Thermodynamic Temperature of High-Temperature Fixed Points Traceable to Blackbody Radiation and Synchrotron Radiation. Int J Thermophys 38, 144 (2017). https://doi.org/10.1007/s10765-017-2273-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10765-017-2273-z