Skip to main content
SpringerLink
Log in

Analysis of the High Frequency Field Expressions at the Caustic Region of a Spherical Reflector Placed in Chiral Medium

  • Published:
Journal of Infrared, Millimeter, and Terahertz Waves Aims and scope Submit manuscript

Abstract

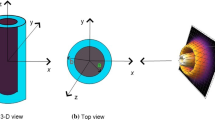
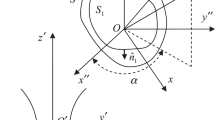
High frequency field expressions are derived around the caustic region of a spherical reflector placed in a homogenous, isotropic and reciprocal chiral medium. Firstly Geometrical Optics (GO) field expressions are derived for the spherical reflector placed in chiral medium. As the GO approximation fails at the vicinity of the caustic therefore, Maslov’s method has been used to find the field expressions which are also valid around the caustic region. Present work is an extension of previous work from two dimensional to three dimensional reflector. Some numerical results including line plots around the focal region of spherical reflector placed in chiral medium are obtained using the derived expressions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. G. A. Dechamps, “Ray techniques in electromagnetics,” Proceedings of the IEEE 60, 1022–1035 (1972).

    Article  Google Scholar 

  2. C. H. Chapman and R. Drummond, “Body wave seismograms in inhomogeneous media using Maslov asymptotic theory,” Bulletin of the Seismological Society of America 72, 277–317 (1982).

    Google Scholar 

  3. V. P. Maslov and V. E. Nazaikinski, Asymptotic of Operator and Pseudo-differential Equations (Consultants Bureau, N.Y., 1988).

  4. R. W. Ziolkowski and G. A. Deschamps, “Asymptotic evaluation of high frequency field near a caustic: An introduction to Maslov’s method,” Radio Science 19, 1001–1025 (1984).

    Article  Google Scholar 

  5. T. Rahim, M. J. Mughal, Q. A. Naqvi, and M. Faryad, “Field around the focal region of a paraboloidal reflector placed in isotropic chiral medium,” Progress in Electromagnetics Research B, PIER B 15, 57–76 (2009).

    Article  Google Scholar 

  6. T. Rahim, M. J. Mughal, Q. A. Naqvi, and M. Faryad, “Paraboloidal reflector in chiral medium supporting simultaneously positive phase velocity and negative phase velocity,” Progress in Electromagnetics Research, PIER 92, 223–234 (2009).

    Article  Google Scholar 

  7. T. Rahim, M. J. Mughal, Q. A. Naqvi, and M. Faryad, “Focal region field of a paraboloidal reflector coated with isotropic chiral medium,” Progress in Electromagnetics Research, PIER (2009).

  8. K. Hongo and Y. Ji, “Study of the field around the focal region of spherical reflector antenna by Maslov’s method,” IEEE Transactions on Antennas and Propagation 36, 592–598 (1988).

    Article  Google Scholar 

  9. M. Faryad and Q. A. Naqvi, “High frequency expression for the field in the caustic region of cylindrical reflector placed in chiral medium,” Progress in Electromagnetics Research, PIER 76, 153-182 (2007).

    Article  Google Scholar 

  10. C. A. Balanis, Advanced Engineering Electomagnetics (John Wiley and Sons, 1989).

  11. A. Lakhtakia, Beltrami Fields in Chiral Media (Contemporary Chemical Physics, World Scientific Series, 1994).

  12. A. Lakhtakia, V. K. Varadan, and V. V. Varadan, editors, Time Harmonic Electromagnetic Fields in Chiral Media (Springer, Berlin, 1989).

    Google Scholar 

  13. D. L. Jaggard, A. R. Mickelson, and C. H. Papas, “On electromagnetic waves in chiral media,” Applied Physics 18, 211216 (1978).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Electronic Engineering, GIK Institute of Engineering Sciences and Technology, Topi, Swabi, 23640, N.W.F.P., Pakistan

    Tariq Rahim & M. J. Mughal

Authors
  1. Tariq Rahim
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. J. Mughal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tariq Rahim.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rahim, T., Mughal, M.J. Analysis of the High Frequency Field Expressions at the Caustic Region of a Spherical Reflector Placed in Chiral Medium. J Infrared Milli Terahz Waves 31, 380–390 (2010). https://doi.org/10.1007/s10762-009-9587-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10762-009-9587-2

Keywords

Search

Navigation