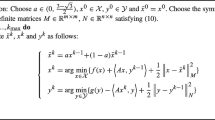Implementation of a maximum clique search procedure on CUDA

Abstract

We present a novel implementation of a Motzkin–Straus-based iterative clique-finding algorithm for GPUs. The well-known iterative approach is enhanced by an annealing variant, where better convergence is obtained by introducing an additional parameter that eliminates certain local maxima, and by an attenuation variant, where the search is repeated several times and known cliques are attenuated by reducing the edge weights. The proposed solution belongs to a global optimization class of methods. It is particularly well suited to large and/or dense graphs, and outperforms other popular clique-finding methods. Therefore, it could be useful in many practical applications related to graph representations of the structures and/or dynamics of complex systems. The proposed algorithm was chosen on the basis of its portability to GPUs. Our implementation includes optimizations aimed at maximizing utilization of GPU cores by delaying some auxiliary computations and performing them simultaneously with the main matrix-vector multiplication. It achieves an average speedup of up to $20\,\times$ over the CPU version, depending on the graph size and density. CUDA-MS is available under the GPL license.

1 Introduction

Formalisms introduced by graph theory are used in various contexts in many fields of research. Graphs are capable of describing various relationships between data items. Thus, specific computational problems can be related to well-researched generic ones. The maximum clique problem is a well-known problem in graph theory. It has been included in Karp’s list of 21 NP-complete problems (Karp 1972).

A graph is an ordered pair $G=\langle V, E \rangle$, where V is a set of nodes and $E \subset V \times V$ is a set of edges. We say that two nodes $n_1, n_2 \in V$ are connected if a corresponding pair is a member of E ($(n_1, n_2) \in E$). A graph may be directed or undirected, depending on whether the pairs in E are ordered or unordered. In this article, we will consider only undirected graphs. A complete graph (clique) is a graph in which all nodes are connected. Any non-trivial graph contains several cliques (every two connected nodes form a clique). Some cliques are maximal with respect to inclusions. The identification of such cliques is called maximal clique enumeration. A simplified version of this problem is to identify the clique of maximal size in a given graph, which is known as the maximum clique problem. Both problems are NP-complete.

Several algorithms, both exact and heuristic, are available for solving the above-mentioned problems. Recent developments using exact algorithms are based on the well-known branch-and-bound scheme, with various approaches following different vertex-coloring strategies (Wu and Hao 2015). The MCQ algorithm (Tomita and Seki 2003) and its refinements, namely MCR (Tomita and Kameda 2007) and MCS (Tomita et al. 2013), use greedy vertex coloring of a subgraph induced by the candidate vertex set for both branching and calculating bounds on the maximum clique size. MCR benefits from a more effective initial sorting of vertices, whereas MCS introduces a novel recoloring procedure. An additional contribution was made by Konc and Janežič, who found that it is not necessary to sort vertices that would not be added to the current clique. This new approximate coloring algorithm and a refined vertex reordering routine were included in MaxCliqueDyn (Konc and Janežič 2007) and its parallel implementation, namely MaxCliquePara (MCP) (Depolli et al. 2013). BB-maxClique (San Segundo et al. 2011) improves upon MCQ and MaxCliqueDyn by exploiting the ability of the CPU to effectively parallelize operations on bit vectors whose size is the same as the CPU word size. FastMaxClique (FMC) (Pattabiraman et al. 2013) and its successor, namely parallel maximum clique (PMC) (Rossi et al. 2013), begin by finding a large clique using a fast heuristic procedure. This solution is later used to impose tight bounds, and it results in aggressive pruning in several consecutive steps in order to provide an exact solution. It has been reported that the heuristic procedure alone is frequently able to find the optimal solution.

Exhaustive exact search is computationally difficult. Therefore, several heuristics have been developed to solve this problem. Reactive local search (Battiti and Protasi 2001) is often considered as a reference method for local search algorithms. Starting with an empty clique, it adds vertices by preferring those with the highest number of adjacent vertices connected to all the vertices that are already in the clique. If further additions are impossible, a vertex is dropped and put into a tabu list. DLS (Pullan and Hoos 2006) and CLS (Pullan et al. 2011) improve upon RLS by introducing randomness when no more vertices can be added to a current clique. In the plateau search phase, vertices are either swapped with those that are not in the clique or dropped on the basis of custom randomized procedures. In contrast to the above-mentioned local search strategies, QUALEX-MS (Busygin 2006) applies a deterministic greedy heuristic that adds vertices in an order depending on their weights derived from the new generalization of the theorem presented by Motzkin and Straus (1965). Ant-Clique (Solnon and Fenet 2006) is a metaheuristic that employs an ant colony optimization to find the best solution. Each ant starts with a random initial vertex and builds a clique by iteratively adding vertices with the highest pheromone factor. Pheromone trails are updated after each ant has constructed a clique. Yet another class of heuristics is represented by EAG (Zhang et al. 2005), a hybrid evolutionary method that uses a guided mutation operator to generate the best results on the basis of parent solutions and a probability model maintained by estimation of distribution algorithms (EDAs).

In this article, we present CUDA-MS, a solution based on the Motzkin–Straus theorem (Motzkin and Straus 1965), which relates the maximum clique problem to the problem of finding the maximum of a certain quadratic form. This heuristic has been shown to be effective in several studies (Bomze et al. 2002; Bomze and Rendl 1998; Pardalos and Xue 1994; Pavan and Pelillo 2003; Pelillo 1999). However, an efficient parallel implementation for graphics processing units (GPUs) has not been demonstrated so far (Cruz et al. 2013).

2 Methods

The adjacency matrix of a graph $G=\langle V,E \rangle$ is an $N \times N$ (where $N=\Vert V\Vert$) matrix whose elements correspond to the connectedness of the edges of the respective nodes. Let $A_G \in {0,1}^{N\times N}$ be the adjacency matrix of G. Assuming that $v_i \in V$ is the ith node of a graph, its elements are given by

$$\begin{aligned} a_{ij}= {\left\{ \begin{array}{ll} 1 &{} \text {if } (v_i, v_j) \in E \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

Let $f_G$ be a quadratic form:

$$\begin{aligned} f_G(x)=x A x^T \end{aligned}$$

Let S be an $N-1$-dimensional unit simplex:

$$\begin{aligned} S=\left\{ x \in R^N : \Vert x\Vert =1 \wedge \forall _{i=1}^N x_i>0 \right\} \end{aligned}$$

where $\Vert x\Vert$ denotes the 1-norm of x:

$$\begin{aligned} \Vert x\Vert =\Vert x\Vert _1=\sum _{i=1}^{N} x_i \end{aligned}$$

We say that $x \in S$ is a characteristic vector of a set $S \subset V$ when $x_i=1/|S|$ if $v_i \in S$ and $x_i=0$ otherwise.

In their study, Motzkin and Straus (1965) presented the relationship between the global maximum of $f_G$ on S and the size of the maximum clique in G.

Theorem 1

(Motzkin–Straus) If $r=\max _{x \in S} f_G(x)$, then G has a maximum clique of size $k=1/(1-r)$. This maximum can be achieved by a characteristic vector of a maximum clique.

This theorem has been developed further to yield the following corollaries.

Corollary 1

If a characteristic vector of a set C is a local maximizer of $f_G$, then C is the maximal clique in G Pelillo (1999).

Corollary 2

Let $A_{G, \alpha }$ be the adjacency matrix of G modified to contain $\alpha$ on the main diagonal:

$$\begin{aligned} A_{G, \alpha } = A_G + \alpha I \end{aligned}$$

where I is an identity matrix. If $x^*$ is a global (or local) maximizer of $f_G=x A_{G,\frac{1}{2}} x^T$ and $r=f_G(x^*)$, then G contains a maximum (maximal)¹ clique of size $k = 1/2(1-r)$ and $x^*$ is its characteristic vector (Bomze and Rendl 1998).

2.1 Replicator equations

Solving a quadratic optimization problem is NP-hard for matrices that are not positive definite (Sahni 1974). However, a simple iterative procedure derived from replicator equations used in evolutionary dynamics may be adopted. It has been shown that a sequence $f_G(x^{(n)})$, where $x^{(n)}$ is defined as

$$\begin{aligned} x^{(n+1)}_i=\frac{x^{(n)}_i \left( A_G \left( x^{(n)}\right) ^T \right) _i}{x^{(n)} A_G \left( x^{(n)}\right) ^T} \end{aligned}$$

(1)

is strictly increasing [$\left( \cdot \right) _i$ denotes the ith element of a vector] (Pelillo 1999). Furthermore, all its elements belong to S. Therefore, iteration starting at any point in S converges to a local maximum of $f_G$, thereby yielding a maximal clique. Next, we demonstrate that in most cases, these local maxima are not far from the global ones.

This method may be applied to $A_G$ as well as $A_{G, 1/2}$. In both cases, $x_n$ converges to a local maximizer of the respective quadratic form. However, in the second case, $x^*$ is guaranteed to be a characteristic vector of a corresponding clique.

It has been observed (Bomze et al. 2002) that for negative values of $\alpha$, the local maxima of $f_G$ may become unstable stationary points of $f_{G,\alpha }$. If C is a clique, the lower bound of $\alpha$ is given by $\gamma _C = \max _{i \notin C} d_C(i)-|C|+1$, where $d_C(i)=\left| \left\{ j \in C: (i,j) \in E \right\} \right|$ is the degree of i with respect to C (i.e., the number of vertices to which i is connected in C). However, $f_{G,\alpha }$ may have other local maxima that do not correspond to any clique.

2.2 Clique-finding heuristics based on replicator equations

It has been established that the local maxima of $f_G$ and $f_{G,\alpha }$ may correspond to maximal cliques (while the global maximum may be related to the maximum clique). The series $x_n$ defined above in (1) may be used straightforwardly to iteratively converge to some local maximum. However, there is no guarantee that the obtained result will give a maximum clique. Three strategies that may converge to different maxima can be applied:

• 1. Iteration of $f_G$: This may converge to a vector $x^*$ that is not a characteristic vector. Nevertheless, $f_G(x^*)$ can be used to obtain the lower bound for the maximum clique size, and it can be shown that the non-zero elements of $x^*$ represent a subgraph with a clique of this size. The eventual cleaning of $x^*$ and extraction of a clique is usually a much simpler problem, and in most cases it can be solved reasonably well by a trivial greedy algorithm. This method was presented in Bomze and Rendl (1998).

• 2. Iteration of $f_{G,1/2}$: In this case, iteration always converges to a characteristic vector. Therefore, no post-processing of the result is required. However, there is no information that would allow for the result to be improved. This scheme was first introduced by Bomze and Rendl (1998).

• 3. Iteration of $f_{G, \alpha }$ for some negative values of $\alpha$: As stated above, the negative values of $\alpha$ make the suboptimal local maxima disappear while simultaneously introducing spurious solutions. This problem may be overcome by the so-called annealing scheme, in which iteration starts with a small value of $\alpha$ that is gradually increased until it reaches $\frac{1}{2}$ and x converges to a characteristic vector. The result is expected to be better than that of the second approach described above. This method was proposed by Bomze et al. (2002).

2.3 Annealing scheme

In principle, it is possible to eliminate a given local maximum corresponding to clique S by choosing $\alpha$ having a smaller value than $\gamma _S$. However, to eliminate all suboptimal maxima, we would have to compute this value for all cliques except the maximum one, which is more complex than computing the maximum clique itself. Therefore, the starting value of $\alpha$ has to be approximated in some other manner.

It has been shown (Bomze et al. 2002) that in random graphs under the Erdős–Rényi model, $\gamma _m = 1 - (1-q)m - \sqrt{(1-q)am} \delta ^{-\frac{1}{2(n-m)}}$ is a lower bound² for $\gamma _S$ with probability $1-\delta$ ($P(\gamma _S \le \gamma _m) \le \delta$), where $m=|S|$. The expected size of the maximum clique can be estimated by using the result given by Matula (1976), who showed that the size of the maximum clique in a random graph of size n and density q for $n\rightarrow \infty$ equals either ${\left\lfloor M(n,q) \right\rfloor }$ or ${\left\lceil M(n,q) \right\rceil }$ with probability tending to 1, where

$$\begin{aligned} M(n,q)=2 \log _\frac{1}{q}n - 2 \log _\frac{1}{q}\log _\frac{1}{q}n + 2 \log _\frac{1}{q}{\frac{e}{2}} + 1 \end{aligned}$$

If M(n, q) is negative, we use the Bollobás estimation of a chromatic number (Bollobás 1988):

$$\begin{aligned} \chi (n, q) \simeq \frac{n}{2 \log (nq)} \log \left( \frac{1}{1-p} \right) \end{aligned}$$

as $np \rightarrow \infty$.

The eventual error in this estimation is overcome by gradually increasing $\alpha$. Thus, the local maxima are gradually enabled, and once the iteration approaches a feasible solution, it is expected to remain close to it and converge to a proper characteristic vector when $\alpha$ reaches $\frac{1}{2}$.

2.4 Attenuation scheme

The annealing method fails when a unique maximal clique competes with a number of smaller ones having a large intersection. Such an ensemble might prove to be a stronger attractor and cause iteration to converge to a spurious solution corresponding to the superposition of all these cliques. Such solutions cannot be eliminated using the annealing approach. In this section, we propose a method to eliminate an interfering solution with a minimal change in the graph.

A particular local maximum x can be removed by adjusting the edge weights between the nodes belonging to its support. It has been observed that edge-weighted graphs and their adjacency matrices exhibit behavior similar to that of unweighted ones (Pavan and Pelillo 2003). However, in this more general case, characteristic vectors corresponding to local maxima may have non-equal values proportional to weights attributed to the respective graph nodes. A set of vertices having a characteristic vector that represents a strict local maximum of $f_G$ is said to be dominant. A dominant set can also be defined by the weights of its members. Specifically, if $S \subseteq V$ is a non-empty set of vertices and $i \in S$, the weight of i with respect to S is defined as

$$\begin{aligned} w_S(i) = {\left\{ \begin{array}{ll} 1 &{} \text {if }|S|=1 \\ \sum \nolimits _{j \in S_i} \phi _{S_i} (j,i) w_{S_i} (j) &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

where $S_i = S {\setminus } \{i\}$ and

$$\begin{aligned} \phi _S(i,j)=a_{ij} - \frac{1}{|S|} \sum _{j \in S} a_{ij} \end{aligned}$$

Moreover, the total weight of S is defined as

$$\begin{aligned} W(S) = \sum _{i \in S} w_s(i) \end{aligned}$$

A set S is said to be dominant if it satisfies the following conditions:

• 1. $w_S(i) > 0$, for all $i \in S$,

• 2. $W(T) > 0$, for any non-empty $T \subseteq S$,

• 3. $w_{S \cup \{i\}}(i) < 0$ for all $i \notin S$.

The first two conditions do not depend on any edge outside the subgraph induced by S, or on uniform scaling of all the edges within a subgraph. The third condition can be transformed [using a lemma presented in Pavan and Pelillo (2003)] into

$$\begin{aligned} \sum _{j \in S} (a_{ij} - a_{hj}) w_S(j) < 0 \end{aligned}$$

for all $i \notin S$ and any $h \in S$. The elements $a_{ij}$ and $a_{hj}$ are the weights of edges outside and inside a subgraph induced by S, respectively. To ensure that a set S is not dominant, we have to apply a scaling factor $\omega$ to the edges inside a clique, which would make the following inequality false for at least one $i \notin S$:

$$\begin{aligned} \sum _{j \in S} (a_{ij} - \omega a_{hj}) w_S(j) < 0 \end{aligned}$$

(2)

This inequality is in fact independent of the choice of h. If S is a dominant set, its characteristic vector $x_S$ is given by

$$\begin{aligned} x_S(i)={\left\{ \begin{array}{ll} \frac{w_S(i)}{W(S)} &{} \text {if }i \in S \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

Therefore, if $x_S$ is a stationary point of $f_G$, then for all $i \in S$,

$$\begin{aligned} \sum _{j \in S} a_{hj} x_S(j) = x_S A x_S^T \end{aligned}$$

The smallest scaling factor for which S remains dominant ($\omega _S$) can be estimated as

$$\begin{aligned} \omega _S = \max _{i \notin S} \frac{(A x_S^T)_i}{x_S A x_S^T} \end{aligned}$$

After finding a local maximum and its support ($x_S$, S), our attenuation algorithm computes a scaling factor ($\omega _S$) and adjusts the adjacency matrix. This step is performed a preset number of times. All the local maxima discovered in the subsequent steps are then refined on the unweighted matrix to ensure that they converge to actual maximal cliques. To accelerate the algorithm, we choose $\omega _S$ such that it falsifies (2) for at least half of the nodes outside S.

2.5 Implementation on GPU

Although matrix-vector multiplication on GPUs is a well-researched problem, efficient implementation of the described iterative procedure is not straightforward. In this section, we describe our choice of the multiplication method, a method for scheduling auxiliary computations such that they do not interfere with the main task and cause less efficient use of available GPU cores (reduced processor load), and an optimization method for minimizing memory usage.

2.5.1 Matrix-vector multiplication

When performing programming tasks on massively parallel architectures, two performance measures must be taken into account. Time efficiency denotes the computation time as a function of the problem size and number of processors. In theoretical models, it is frequently assumed that the number of processors is unlimited; thus, the time efficiency is useful for assessing the efficiency of the algorithm, albeit in unrealistic settings. On the other hand, work efficiency reflects the total time consumed by all the processors used for computation. Therefore, whenever an instance of a problem is small, a time-efficient algorithm should be used. If the number of available processors (CUDA cores in our case) is small compared to the instance size, then a work-efficient algorithm is more beneficial.

The design of CUDA processors requires programmers to implement self-contained functions (kernels) that are launched in a specified number of instances. Furthermore, single threads in a kernel run are grouped into warps, blocks, and a grid. The number of threads in a block, the number of blocks in a grid, and their dimensional structures are given by the programmer. The warp size is hardware-dependent and equals 16. The threads in a warp are executed synchronously; they should have uniform memory accesses and as little divergence on conditional statements as possible. Taking these factors into consideration, we implemented two multiplication algorithms and tested their efficiency for matrices of different sizes.

In the case of smaller matrices (less than $1024 \times 1024$), we opted for an algorithm in which each block is assigned to compute the scalar product of a single matrix row and a vector x. Such an algorithm is not optimal in terms of time efficiency, because when computing the sum of elements in an array (known as reduction), some processors become idle before the end of the computation. However, for smaller matrices, the algorithm allows a sufficient number of threads to be started in order to hide memory latency.

Fig. 1

Diagram illustrating parallelization of matrix-vector multiplication. A matrix $A_G$ is split into blocks of rectangular submatrices, each to be multiplied by the respective part of a vector $x_n$ with threads iterating over the submatrix columns. In the second stage, the partial results are summed up

For larger matrices, we used a more advanced method that splits a matrix into rectangular submatrices and assigns a block to each of them. Each such block computes the product of a submatrix with the respective fragment of a vector³ (see Fig. 1). These results are stored in temporary vectors—one for each column of submatrices. In the second stage, the temporary vectors are added. This solution theoretically allows for full occupancy of all available cores, assuming that the matrix is sufficiently large.

2.5.2 Concurrent execution of kernels

While computing the matrix-vector product is the most computationally intensive task, there are several other tasks that have to be executed, either for every matrix multiplication or once for a few multiplications. Computing $x^{(n+1)}$ from $x^{(n)}$, as expressed by (1), involves multiplication and normalization. Normalization involves a simple computation of the sum of vector elements. It is simple (i.e., it requires little work), but it is not time-efficient. It is also impossible to use all CUDA cores, even in the case of large graphs. To achieve better GPU utilization, instead of normalizing $x^{(n)}$ before computing $x^{(n+1)}$, we delay this task and perform it simultaneously with multiplication. Specifically, we compute the following series:

$$\begin{aligned} y^{(0)}&= x^{(0)} \\ y_i^{(2n+1)}&= y_i^{(2n)} \left( A_G \left( y^{(2n)} \right) ^T\right) _i \\ y^{(2n+2)}_i&=\frac{ y^{(2n+1)}_i \left( A_G \left( y^{(2n+1)} \right) ^T\right) _i }{\Vert y^{(2n)} \Vert ^ 4} \end{aligned}$$

It is easy to see that for all n

$$\begin{aligned} \frac{y^{(n)}}{\Vert y^{(n)} \Vert } = x^{(n)} \end{aligned}$$

We prove that by induction. For $n=0$ it follows from the definition of $y^{(n)}$. Assuming that $\frac{y^{(2n)}}{\Vert y^{(2n)} \Vert } = x^{(2n)}$, and taking $z_n= x^{(n)} A_G \left( x^{(n)} \right) ^T$ we see that:

$$\begin{aligned} y_i^{(2n+1)}= & {} y_i^{(2n)} \left( A_G \left( y^{(2n)} \right) ^T\right) _i = x_i^{(2n)} \left( A_G \left( x^{(2n)} \right) ^T\right) _i \left\| y^{(2n)} \right\| ^2 \\= & {} x_i^{(2n+1)} z_{2n} \left\| y^{(2n)} \right\| ^2\\ y_i^{(2n+2)}= & {} \frac{y_i^{(2n+1)} \left( A_G \left( y^{(2n+1)} \right) ^T\right) _i }{\left\| y^{(2n)} \right\| ^ 4}\\= & {} x_i^{(2n+1)} \left( A_G \left( x^{(2n+1)} \right) ^T\right) _i z_{2n}^2 = x_i^{(2n+2)} z_{2n+1} z_{2n}^2 \end{aligned}$$

Therefore $y^{(n)}$ after normalization equals $x^{(n)}$.

2.5.3 Storing adjacency matrix

By assuming that dense graphs are the most challenging graphs for clique finding, we decided against using sparse matrices. In our opinion, the overhead incurred by nonuniform memory accesses does not justify the gain in memory efficiency. However, to limit memory usage, we opted to use a single byte for each matrix element. This is less effective than using a single bit for each edge, but it allows to store the edge weights. Integer values (falling in the range [1, 255]) are converted into real numbers by using the following formula

$$\begin{aligned} w_{ij} = p^{(a_{ij}-1)^2} \end{aligned}$$

where p is chosen to minimize the largest gap between consecutive elements of a sequence $\left\{ 1, p^{1^2}, p^{2^2}, p^{3^2}, \ldots , p^{254^2}, 0 \right\}$.

2.5.4 Final remarks

In this study we have refrained from using available implementations of matrix multiplication in order to limit memory footprint and exploit peculiarities of graph adjacency matrices. Apart from the attenuation scheme, elements of the adjacency matrix can take only two values: 0 and 1 (with the exception of the diagonal, which is processed separately). This means that instead of multiplication a simpler and more effective conditional instruction can be used to determine, whether a particular element of x should be added to the dot product. Furthermore, as stated in section above, in the attenuation scheme our implementation stores weights as integer exponents. This is done to save memory space, and requires decoding of the weights during multiplication. These two optimizations, which either allow to avoid multiplications altogether or enable processing large graphs, cannot be achieved by using standard libraries, and outperform methods optimized for generic matrix multiplication.

3 Results

The developed algorithms were tested on a well-established DIMACS set as well as a set of large random graphs generated by us. The results were compared with those of the following reference methods: ANT (Solnon and Fenet 2006), EAG (Zhang et al. 2005), MCP (Depolli et al. 2013), FMC (Pattabiraman et al. 2013), PMC (Rossi et al. 2013), QUALEX-MS (Busygin 2006). Because the main goal of this study is to develop a method capable of delivering reasonably good results in a short time for large graphs, we focused on evaluating the time efficiency of the tested algorithms. To make our measurements comparable, we carried out all the computations on a single core of an Intel Xeon E5-2650 (2 GHz, Sandy Bridge, Q1’12) CPU or an nVidia Tesla K20 GPU (Q4’12).⁴

However, one cannot assess the performance of heuristic algorithms that may be designed with emphasis on accuracy versus efficiency by comparing the computation times directly. Therefore, apart from separately presenting computation times and quality, we have used performance profiles (Dolan and Moré 2002) to compare times of successful calculations for different levels of the required accuracy. Assuming that $t_{g,m}$ and $a_{g,m}$ are, respectively, computation time and ratio of obtained clique size to the largest one known for a graph g and method m, we define time ratio as:

$$\begin{aligned} r_{g,m} = \frac{t_{g,m}}{\min _m t_{g,m}} \end{aligned}$$

and accuracy ratio as:

$$\begin{aligned} s_{g,m} = \frac{a_{g,m}}{\max _m a_{g,m}} \end{aligned}$$

These ratios are aggregated into profiles for each method:

$$\begin{aligned} \rho _m(\tau )= & {} \frac{| g \in \mathcal {G} : r_{g,m} \le \tau | }{| \mathcal {G}|}\\ \sigma _m(\alpha )= & {} \frac{| g \in \mathcal {G} : s_{g,m} \ge \alpha | }{| \mathcal {G}|} \end{aligned}$$

where $\mathcal {G}$ is a set of graphs, and $| \cdot |$ denotes set cardinality. According to Dolan and Moré performance profiles may be interpreted as probabilities for a method to achieve performance not worse than of the best method by a given ratio. We have computed such profiles for computation time and accuracy. To combine these two measures we have also created time profiles for a given minimal accuracy, substituting computation time in cases where clique size was unsatisfactory with a large number:

$$\begin{aligned} r_{g,m}(a_{\min })= & {} {\left\{ \begin{array}{ll} \frac{t_{g,m}}{\min _m t_{g,m}} &{} a_{g,m}\ge a_{\min } \\ \infty &{} \text {otherwise} \end{array}\right. }\\ \rho _m(\tau , a_{\min })= & {} \frac{| g \in \mathcal {G} : r_{g,m}(a_{\min }) \le \tau | }{| \mathcal {G}|} \end{aligned}$$

Performance profiles can be compared directly by visual inspection, but when they depend on an additional threshold, more insight can be gained by computing area under the curve (AUC) for each method and different values of $a_{\min }$.

The results are presented for four variants of the algorithm:

• 1. iteration of $f_G$ denoted as $\alpha =0$,

• 2. iteration of $f_{G, 1/2}$ denoted as $\alpha =\frac{1}{2}$,

• 3. annealing scheme,

• 4. attenuation scheme.

Both annealing and attenuation algorithms start with $\alpha =-\,4.5$, which is then increased by 1 in each iteration. The attenuation algorithm computes at most 15 cliques, and it is terminated if the last clique is smaller than $60\%$ of the largest clique found. The results of the variants with starting values of $\alpha$ computed individually for each graph (see Sect. 2.3) are less promising and have been included in the Supplementary Materials.

3.1 DIMACS graphs

The graphs in the DIMACS Challenge set have been designed (or chosen) to be particularly complex, and they exhibit NP-completeness of the clique-finding problem (Sanchis 1995). Several graph families in this set either contain concealed cliques whose size is much greater than expected, based on graph size and density (brock), or are highly regular with several instances of cliques having the maximal size (hamming, johnson, keller, MANN). It can be seen that such families pose a significant difficulty for the presented method (see Fig. 2). In many cases, better results can be achieved using the annealing scheme. The attenuation scheme may be regarded as the last resort because it seldom offers any improvement over the annealing method. It should be noted that although our implementation has been designed to deal with large graphs, it achieves good performance even on smaller ones. Moreover, on small and less dense graphs, CPU implementation is more advantageous than GPU implementation because the CPU implementation uses a sparse matrix representation of a graph, and it is impossible to achieve a sufficient degree of parallelization for smaller graphs. Simple iteration (both for $\alpha =0$ and $\alpha =\frac{1}{2}$) was the fastest among the tested methods; its average quality (fraction of the maximal clique discovered) was $79\%$ and the total computation time was 7 s. By comparison, the average quality of the fastest reference method, namely PMC, was $81\%$, but the total computation time required was nearly 1 min (for other methods see Table 1).

Performance profiles indicate that the reference methods can be roughly divided into two groups (Fig. 3a, c). ANT, EAG, MCP and QUALEX-MS are accurate but slow. FMC and PMC are faster but at the expense of accuracy. Our attenuation scheme falls between these groups both in accuracy and efficiency, while simple iteration is slightly worse than PMC. However, when taking the minimal accuracy level $a_{\min }=0.8$ attenuation scheme is outperformed only by QUALEX-MS and ANT (Fig. 3b). This result is fairly robust. When comparing AUC for higher accuracy levels, one more method—MCP gains advantage. PMC loses its lead for accuracy levels over 0.75 (Fig. 3d). The DIMACS set contains several small graphs for which GPU computation is not suitable, therefore for each graph and each method we have chosen a shorter computation time from CPU and GPU runs.⁵

Fig. 2

Clique sizes normalized by the size of the largest known clique (a) and computation times (b), as well as ranks of the CUDA-MS variants with respect to the reference methods for graphs in the DIMACS set. The thick line denotes the PMC method, which seems to have a ratio of accuracy versus efficiency that is the most similar to the presented methods, and therefore is the most directly comparable method

Fig. 3

Time performance profiles for graphs in the DIMACS dataset calculated for all computations (a) and for computations with at least 0.8 accuracy (b), as well as accuracy profiles (c), and plot of AUC for time profiles depending on minimal accuracy (d). The thick line denotes the PMC method

3.2 Large random graphs

The largest graph in the DIMACS set contains only 4000 nodes. Therefore, to test the computational efficiency, we generated larger graphs with the number of nodes varying between 4096 and 32,768. The first family was generated with an Erdős-Rényi model (Gilbert 1959), in which an edge between each pair of nodes is added with a constant probability. A clique comprising a given number of randomly chosen vertices was then embedded in these graphs. Graphs in this family have names derived from the template $\texttt {bern\_}n\texttt {\_}p\texttt {\_}c$, where n is the number of nodes, p is the edge probability, and c is the size of the embedded clique (results are presented in Fig. 4). The second family follows a scale-free model proposed by Albert and Barabási (2002) in which nodes with a given number of edges (k) are consecutively added to a graph with edge connectivity drawn from a distribution proportional to the vertices’ degrees. A few such graphs can be superimposed to obtain a graph containing several maximal cliques and slightly randomized to make the maximal cliques less obvious. These graphs’ names are derived from the template $\texttt {bara\_}n\texttt {\_}k\texttt {\_}m$, where n is the number of nodes, k is the number of edges incident to a newly added node, and m is the number of scale-free graphs to be superimposed (results are presented in Fig. 5).

Fig. 4

Clique sizes normalized by the size of the largest known clique (a) and computation times (b), as well as ranks of the CUDA-MS variants with respect to the reference methods for graphs in the Bern set. The thick line denotes the PMC method which seems to have a ratio of accuracy versus efficiency that is the most similar to those of the presented methods, and therefore is the most directly comparable method

Fig. 5

Clique sizes normalized by the size of the largest known clique (a) and computation times (b) as well as ranks of the CUDA-MS variants with respect to the reference methods for graphs in the Bara set. The thick line denotes the PMC method, which seems to have a ratio of accuracy vs. efficiency that is the most similar to those of the presented methods and is thus the most directly comparable method

Fig. 6

Time performance profiles for graphs in the Bern and Bara datasets calculated for all computations (a) and for computations with at least 0.8 accuracy (b), as well as accuracy profiles (c), and plot of AUC for time profiles depending on minimal accuracy (d). The thick line denotes the PMC method

Fig. 7

Clique sizes normalized by the size of the largest known clique (a) and computation times (b) as well as ranks of the CUDA-MS variants with respect to the reference methods for graphs in the BernM set. The thick line denotes the PMC method, which seems to have a ratio of accuracy versus efficiency that is the most similar to those of the presented methods and is thus the most directly comparable method

The presented methods demonstrated their effectiveness on large graphs. The average quality of simple iteration was in the range of 80–83 with a computation time of ${\sim }\,1100\;\mathrm {s}$ (the annealing scheme achieved $91\%$ accuracy in ${\sim }\,2300\;\mathrm {s}$), while the average quality of the fastest reference method was $77\%$ with a the computation time of ${\sim }\,7700\;\mathrm {s}$ (for other methods see Table 1). Some methods failed for larger graphs (EAG for graphs having 8192 or more nodes, MCP and QUALEX-MS for graphs having 32,768 nodes). Figures 4b and 5b show that simple iteration and the annealing scheme are invariably faster than the reference methods. Performance profiles (Fig. 6) clearly confirm these observations. ANT and QUALEX-MS are the only methods that may be considered to outperform the attenuation scheme when highest degrees of accuracy are required. However, QUALEX-MS fails for the largest graphs, while ANT is on average five times slower than the attenuation scheme and one hundred times slower than the annealing scheme.

Table 1 Average clique size and the total computation time

4 Random graphs with high density alternative solutions

As seen in the results on the DIMACS set, presented methods tend to underperform on graphs, which have several instances of large, but not maximum-sized cliques (such as Keller graphs). In such cases local maxima related to these may turn out to be stronger attractors than global maxima corresponding to optimal solutions. We have developed a set of random graphs containing an ensemble of cliques of the same size, and optionally containing a single instance of a larger clique. The goal was to check, if our methods work well on such ensembles of cliques (i.e. if it is possible to break symmetries and converge to a single optimal solution), as well as to see, if they are sensitive enough to detect a single instance of the largest clique, when it is shadowed by an ensemble.

These graphs have been generated using an Erdős–Rényi model. A random graph has been injected with a clique, and then each node in a clique has been replaced with a number of its copies—each copy connected to the same nodes as the original, copies of one node are not connected to each other. The number of copies for each node was randomly derived from a Poisson distribution with mean equal to 2. The size of the starting random graph was chosen based on the number of copies pre-drawn for each node in order to achieve a desired size of the whole graph. Such graphs have an exponential (with respect to the clique size) number of overlapping cliques. Each graph generated this way has been further augmented by randomly choosing a number of nodes and connecting them with edges to create another single instance of a clique. Names of graphs in this family conform to the pattern $\texttt {bernm\_}n\texttt {\_}p\texttt {\_}c_1\texttt {\_}c_2$, where n is the number of nodes in the graph, p is the edge probability in the Erdős-Rényi model, $c_1$ is the size of a multiplicated clique, and $c_2$ is the size of a single competing clique.

Fig. 8

Time performance profiles for graphs in the BernM dataset calculated for all computations (a) and for computations with at least 0.8 accuracy (b), as well as accuracy profiles (c), and plot of AUC for time profiles depending on minimal accuracy (d). The thick line denotes the PMC method

This dataset turned out to be significantly more difficult for several methods. However, in case of branch-and-bound heuristics corresponding graphs in the bern set without multiplicated nodes were also often solved suboptimally. Replacing a single clique with an ensemble and introducing another slightly larger one doesn’t influence the achieved accuracy. In case of presented methods, it can be observed, that graphs with multiple optimal solutions are solved similarly as their single solution counterparts. However, if a graph contains a slightly larger clique, simple iterations regardless of $\alpha$, as well as, the annealing scheme do not converge to the optimal solution (Fig. 7). The attenuation scheme, on the other hand, usually succeeds. Despite a much higher computation time than in the case of the annealing scheme it is still the fastest effective method tested (see Table 1 and Fig. 8).⁶

5 Conclusions

In this study, we presented a suite of heuristic clique-finding algorithms based on the Motzkin–Straus theorem. In addition, we described their CPU and GPU implementations (using CUDA technology). Our results indicated that the presented algorithms are suited particularly well for approximating the maximal clique in large graphs having several thousand vertices, on which they were shown to outperform the other tested methods. The average accuracy was around 80% for graphs in the DIMACS set and up to 93% for large random graphs generated by us for the purpose of this study. For these graphs, CUDA-MS outperformed all the reference methods by a large margin. The less promising results for the DIMACS graphs may be attributed to the fact that these graphs are particularly complex even though they are designed to be fairly small. The presented heuristics are essentially variants of a hill-climbing procedure. Therefore, whenever the explored landscape lacks significant features, they are likely to converge to a suboptimal local solution. In such cases, local search methods seem to have an advantage, especially for smaller graphs. However, the situation is opposite in the case of large graphs. Local searches tend to fail even in the case of graphs for which no significant effort to conceal the largest clique was made. Artificially generated graphs with high levels of symmetry, such as Keller graphs, constitute an especially complex category. A large number of equivalent vertices that exhibit the same behavior during iteration preclude convergence to useful maxima. Test on random graphs containing several overlapping maximal cliques indicate, that this problem is less significant, if strict symmetry of a clique is broken by randomness of the rest of the graph. Nevertheless, it is still possible that a dense ensemble of large cliques could dominate a single instance of the maximal one. This problem can be overcome by the attenuation scheme, which augments the graph to make less prominent solutions stand out.

We documented the significant speed advantage afforded by the GPU implementation. The mean speedups for graphs having 8192 or more vertices were in the range of 18–20 times. Lower speedups were achieved for smaller or less dense graphs, where either sufficient occupancy of GPU cores could not be achieved or sparse matrix implementation was more effective. Although the benchmarks presented in this study were computed using high-end nVidia Tesla GPUs, all floating-point calculations were performed in the single-precision format. Therefore, similar performance should be expected using a more affordable GeForce hardware. Furthermore, computations have been carried on hardware manufactured in 2012. Since that time GPUs have gained even larger performance advantage over CPUs. Therefore, it can be reasonably expected, that even larger speedups could be achieved on contemporary hardware.

6 Availability

CUDA-MS is available under the GPL v3 license at http://github.com/pawelld/CUDA-MS.