Spherically-symmetric solutions in general relativity using a tetrad-based approach

Abstract

We present a tetrad-based method for solving the Einstein field equations for spherically-symmetric systems and compare it with the widely-used Lemaître–Tolman–Bondi (LTB) model. In particular, we focus on the issues of gauge ambiguity and the use of comoving versus ‘physical’ coordinate systems. We also clarify the correspondences between the two approaches, and illustrate their differences by applying them to the classic examples of the Schwarzschild and Friedmann–Lemaître–Robertson–Walker spacetimes. We demonstrate that the tetrad-based method does not suffer from the gauge freedoms inherent to the LTB model, naturally accommodates non-uniform pressure and has a more transparent physical interpretation. We further apply our tetrad-based method to a generalised form of ‘Swiss cheese’ model, which consists of an interior spherical region surrounded by a spherical shell of vacuum that is embedded in an exterior background universe. In general, we allow the fluid in the interior and exterior regions to support pressure, and do not demand that the interior region be compensated. We pay particular attention to the form of the solution in the intervening vacuum region and illustrate the validity of Birkhoff’s theorem at both the metric and tetrad level. We then reconsider critically the original theoretical arguments underlying the so-called $R_{\mathrm{h}} = ct$ cosmological model, which has recently received considerable attention. These considerations in turn illustrate the interesting behaviour of a number of ‘horizons’ in general cosmological models.

1 Introduction

Spherically-symmetric solutions in general relativity are of fundamental importance to the study of compact objects, black holes and cosmology. Indeed, two of the oldest and most commonly studied exact solutions of Einstein’s field equations are spherically symmetric: the Schwarzschild metric [1] describes the gravitational field outside a static spherical massive body, and the Friedmann–Lemaître–Robertson–Walker (FLRW) metric [2,3,4,5,6,7,8] describes a homogeneous and isotropic universe in terms of the evolution of its scale factor with cosmic time. Moreover, it was not long before McVittie [9, 10] combined the Schwarzschild and FLRW metrics to produce a new spherically-symmetric solution that describes a point mass embedded in an expanding universe, although there still remains some debate regarding its physical interpretation [11, 12].

Subsequently, there have been numerous studies of the general-relativistic dynamics of self-gravitating spherical systems. For example, Misner et al. [13] describe the spherically-symmetric collapse of a ‘ball of dust’ having uniform density and zero pressure that is embedded in a static vacuum exterior spacetime, and later generalise their results to incorporate pressure internal to the object. By contrast, ‘Swiss cheese’ models [14] consider an exterior expanding FLRW universe, albeit pressureless, in which a pressureless spherical object is embedded and surrounded by a ‘compensating void’ that itself expands into the background and ensures that there is no net gravitational effect on the exterior universe.

A more realistic description than the Swiss cheese models is provided by models based on the Lemaître–Tolman–Bondi (LTB) solution [15,16,17]. Such models can incorporate an arbitrary (usually continuous) density profile for the central object, which is usually not compensated but can be made so by an appropriate choice of initial radial density and velocity profiles. Nonetheless, these models again assume both the interior and exterior regions to be pressureless, although it is possible to accommodate cosmological models with uniform pressure [18, 19]. The standard LTB metric can be extended to include non-uniform pressure but only when it is anisotropic [20,21,22]. Lastly, a more generalised version of the LTB solutions has been presented in [23] to describe a central object with pressure embedded in a static vacuum exterior.

A recent resurgence of interest in Swiss cheese and LTB models has been prompted by the possibility that they may provide an explanation for observations of the acceleration of the universal expansion, without invoking dark energy. This might occur if we, as observers, reside in a part of the universe that happens to be expanding faster than the region exterior to it. By observing a source in the exterior region, one would then measure an apparent acceleration of the universe’s expansion, but this would be only a local effect. The effects of local inhomogeneities on the apparent acceleration of the universe have been widely studied [24,25,26,27,28,29,30,31], and have been linked with the observations of distant Type-Ia supernova. However it has been shown that such models would induce variations in the CMB black-body spectrum through scattering, which disagrees with observations [32, 33]. In addition, LTB models have been used to study the effects of inhomogeneities on observed cosmological parameters, such as the Hubble constant [34,35,36], and to calculate effects of a void as a possible explanation for the cold spot in the cosmic microwave background (CMB) [37, 38].

The LTB model does, however, have some limitations. In addition to the usual restriction to pressureless systems, the LTB model is typically expressed in comoving coordinates and thus provides a Lagrangian picture of the fluid evolution that can be difficult to interpret. More importantly, the LTB metric contains a residual gauge freedom that necessitates the imposition of arbitrary initial conditions to determine the system evolution.

As a consequence, we have for some time adopted a different, tetrad-based method for solving the Einstein field equations for spherically-symmetric systems. The method was originally presented in [39] in the language of geometric algebra, and was recently re-expressed in more traditional tetrad notation in [40, 41]. The advantages of the approach are that it can straightforwardly accommodate non-uniform pressure, has no gauge ambiguities (except in vacuum regions, as we shall discuss later) and is expressed in terms of a ‘physical’ (non-comoving) radial coordinate. As a result, the method has a clear and intuitive physical interpretation. Indeed, the gauge choices employed result in equations that are essentially Newtonian in form.

In [42, 43], we applied the method to modelling the evolution of a finite-size, spherically-symmetric object with continuous radial density and velocity profiles that is embedded in an expanding background universe (either spatially-flat, open or closed) and compensated so that it does not exert any gravitational influence on the exterior universe; the fluid was assumed to be pressureless throughout. In [40], we used the method to obtain solutions describing a point mass residing in either a spatially-flat, open or closed expanding universe containing a cosmological fluid with pressure. In the spatially-flat case, a simple coordinate transformation relates our solution to the corresponding one derived by McVittie, but for spatially-curved cosmologies our metrics are physically distinct from the corresponding McVittie metrics, as shown in Section 3.2 in [40]. Hence, we believe that the latter in fact do not necessarily describe spatially-curved cosmologies with a point mass in the centre, even though they may be solutions of Einstein’s equations. In [41], we extended this study by applying the tetrad-based approach to obtain the solution describing the evolution of a finite spherical region of uniform interior density that is embedded in a background of uniform exterior density, where the fluid in both regions can support pressure and the expansion (or contraction) rates of the two regions are expressed in terms of interior and exterior Hubble parameters that are, in general, independent. We also derived a generalised form of the Oppenheimer–Volkov equation, valid for general time-dependent, spherically-symmetric systems.

In this paper, we present a comparison of our tetrad-based methodology with the LTB model for solving the Einstein field equations for spherically-symmetric systems. In particular, we focus on the issues of gauge ambiguity and the use of comoving versus ‘physical’ coordinate systems. We also clarify the correspondences, where they exist, between the two approaches. In addition, we extend the analysis presented in [41] by applying our tetrad-based method to a generalised form of ‘Swiss cheese’ model, which consists of an interior spherical region surrounded by a spherical shell of vacuum that is embedded in an exterior background universe. In general, we allow the fluid in the interior and exterior regions to support pressure, and we demand neither that the interior region be compensated, nor that the interior and exterior regions be uniform. Nonetheless, our principal focus is the case in which the fluid in the interior and exterior regions has uniform (although, in general, different) densities. In particular, we pay special attention to the form of the solution in the intervening vacuum region and verify the validity of Birkhoff’s theorem, the usual interpretation of which has recently been brought in question [44]. This investigation allows us to reconsider critically the original theoretical arguments underlying the so-called $R_{\mathrm{h}} = ct$ cosmological model [45], which has recently received considerable attention. These considerations in turn elucidate the behaviour of a number of ‘horizons’ during the general-relativistic evolution of a spherically-symmetric self-gravitating matter distribution, which does not appear to have been widely discussed in the literature.

The structure of this paper is as follows. In Sect. 2, we outline our tetrad-based approach to solving the Einstein equations. In Sect. 3 we compare our approach to the more commonly-used LTB model. Note that the comparison serves as a pedagogical outline which presents the physical motivations behind each approach, with the aim of highlighting the advantages of using the tetrad-based method and ‘physical’ coordinates, by applying both methods to the familiar FLRW and Schwarzschild spacetimes. We then present original results, where we apply our tetrad-based method to describe the evolution of a generalised form of ‘Swiss cheese’ model in Sect. 4 and investigate the validity of Birkhoff’s theorem in its vacuum region in Sect. 5. We discuss the $R_{\mathrm{h}} = ct$ cosmology in Sect. 6 and describe the generic evolution of a number of cosmological ‘horizons’ in Sect. 7. Finally, we present our conclusions in Sect. 8. We adopt natural units $c=G=1$ throughout.

2 Tetrad-based solution for spherical systems

In a Riemannian spacetime in which events are labelled with a set of coordinates $x^{\mu }$, each point has the corresponding coordinate basis vectors $\mathbf {e}_{\mu }$, related to the metric via $\mathbf {e}_{\mu }\cdot \mathbf {e}_{\nu }=g_{\mu \nu }$. At each point we may also define a local Lorentz frame by another set of orthogonal basis vectors $\hat{\mathbf {e}}_a$ (Roman indices), which are not derived from any coordinate system and are related to the Minkowski metric $\eta _{ab}=\text{ diag }(1,-1,-1,-1)$ via $\hat{\mathbf {e}}_a\cdot \hat{\mathbf {e}}_b=\eta _{ab}$. The relationship between the two sets of basis vectors is defined in terms of tetrads, or vierbeins ${e_{a}}^{\mu }$, where the inverse is denoted ${e^{a}}_{\mu }$:

$$\begin{aligned} \hat{\mathbf {e}}_a={e_{a}}^{\mu }\mathbf {e}_{\mu },\quad \mathbf {e}_{\mu }={e^{a}}_{\mu }\hat{\mathbf {e}}_a. \end{aligned}$$

(1)

It is not difficult to show that the metric elements are given in terms of the tetrads by $g_{\mu \nu }=\eta _{ab}e^a_{\ \mu }e^b_{\ \nu }$.

The local Lorentz frames at each point define a family of ideal observers whose worldlines are the integral curves of the timelike unit vector field $\hat{\mathbf {e}}_0$. Along a given worldline, the three spacelike unit vector fields $\hat{\mathbf {e}}_i$ $(i=1,2,3)$ specify the spatial triad carried by the corresponding observer.

For our spherically-symmetric system, we work in terms of the tetrad components $f_1={e_{0}}^{0}$, $g_1 = {e_1}^{1}$ and $g_2 = {e_0}^{1}$, as described in [40], which define the system via the line-element

$$\begin{aligned} ds^2=\frac{g_1^{2}-g_2^{2}}{f_1^{2}g_1^{2}}\,dt^2+\frac{2g_2}{f_1g_1^{2}} \,dt\,dr-\frac{1}{g_1^{2}}\,dr^2-r^2d\varOmega ^2. \end{aligned}$$

(2)

where $d\varOmega$ is an element of solid angle and we have adopted a ‘physical’ (non-comoving) coordinate¹ for which the proper area of a sphere of radius r is $4\pi r^2$.

Finally, the remaining gauge freedom (which leaves the line-element unchanged) can be employed (at least in non-vacuum regions) to choose the timelike unit frame vector $\hat{\mathbf {e}}_0$ at each point to coincide with the four-velocity of the fluid at that point. Thus, by construction, the four-velocity $\mathbf {v}$ of a fluid particle (or an observer comoving with the fluid) has components $[\hat{v}^a] = [1,0,0,0]$ in the tetrad frame. Since $v^{\mu }=e_a^{\ \mu }\hat{v}^a$, the four-velocity may be written in terms of the tetrad components and the coordinate basis vectors as $\mathbf {v}= f_1 \mathbf {e}_0 + g_2 \mathbf {e}_1$. Thus, the components of a comoving observer’s four-velocity in the coordinate basis are simply $[v^\mu ] \equiv [\dot{t},\dot{r},\dot{\theta },\dot{\phi }]=[f_1,g_2,0,0]$, where dots denote differentiation with respect to the observer’s proper time $\tau$.

As a consequence of this final gauge choice, it is convenient to define the two linear differential operators

$$\begin{aligned} L_t&\equiv f_1\partial _t+g_2\partial _r,\nonumber \\ L_r&\equiv g_1\partial _r. \end{aligned}$$

(3)

We may identify $L_t$ as the derivative with respect to the proper time of a comoving observer, since $L_t = \dot{t}\partial _t + \dot{r}\partial _r = d/d\tau$, and similarly one may show that $L_r$ coincides with the derivative with respect to the radial proper distance of a comoving observer. Moreover, since $g_2$ is the rate of change of the r coordinate of a fluid particle with respect to its proper time, it can be physically interpreted as the fluid 3-velocity. We will therefore, in general, use $g_2$ and v interchangeably in our analysis.

It is also convenient to introduce explicitly the spin-connection coefficients $F \equiv {\omega ^0}_{11}$ and $G \equiv {\omega ^1}_{00}$, as described in [40], which are both, in general, functions of t and r. Since we are assuming standard general relativity, however, for which torsion vanishes, the spin-connection coefficients can be written entirely in terms of the tetrad components and their derivatives. For the torsion to vanish and for the resulting Riemann tensor to satisfy its Bianchi identity, the spin-connection coefficients F and G and the non-zero tetrad components $f_1$, $g_1$ and $g_2$ must satisfy the relationships

$$\begin{aligned} L_rf_1&=-Gf_1\Rightarrow f_1=\exp \left\{ -{\textstyle \int ^r\frac{G}{g_1}dr}\right\} ,\nonumber \\ L_r g_2&= Fg_1 ,\nonumber \\ L_t g_1&= Gg_2,\phantom {f_1=\exp \left\{ -{\textstyle \int ^r\frac{G}{g_1}dr}\right\} } \end{aligned}$$

(4)

where the explicit solution for $f_1$ contains no arbitrary function of t, because one can always be absorbed by a further t-dependent rescaling of the time coordinate (which does not change $f_2$).

For matter in the form of a perfect fluid with proper density $\rho$ and isotropic rest-frame pressure p, the Einstein field equations and the contracted Bianchi identities lead to the following system² of dynamical and continuity equations [39]

$$\begin{aligned} L_r p&=-G(\rho +p),\nonumber \\ L_rM&=4\pi g_1 r^2\rho ,\nonumber \\ L_t\rho&=-\left( \frac{2g_2}{r}+F\right) (\rho +p),\nonumber \\ L_t M&=-4\pi g_2 r^2p, \end{aligned}$$

(5)

where we have defined the function of t and r (in general)

$$\begin{aligned} M\equiv \tfrac{1}{2}r\left( g_2^{2}-g_1^{2}+1-\tfrac{1}{3}\varLambda r^2\right) , \end{aligned}$$

(6)

and $\varLambda$ is the cosmological constant and M is the Misner-Sharp mass.

The physical interpretation of the functions F, G and M is straightforward. As shown in [40], for an object in general radial motion (not necessarily co-moving with the fluid) with four-velocity components $[\hat{u}^a] = [\hat{u}^0,\hat{u}^1,0,0]$ in the tetrad frame, the corresponding components of the object’s four-acceleration are

$$\begin{aligned} \hat{a}^0&=\dot{\hat{u}}^0+G\hat{u}^0\hat{u}^1+F(\hat{u}^1)^2,\nonumber \\ \hat{a}^1&=\dot{\hat{u}}^1+G(\hat{u}^0)^2+F\hat{u}^0\hat{u}^1, \end{aligned}$$

(7)

and its proper acceleration is $\alpha = \sqrt{-\hat{a}^b\hat{a}_b}$, which provides a physical interpretation of the functions F and G. In particular, for the special case in which the object is co-moving with the fluid, one has $[\hat{u}^b] = [1,0,0,0]$ and so $[\hat{a}^b] = [0,G,0,0]$. Thus the proper acceleration of a fluid particle is $\alpha = G$ in the radial direction. Indeed, the $L_rp$-equation in (5) shows that, in the absence of a pressure gradient, G vanishes and so the motion becomes geodesic. The physical interpretation of the function M can be obtained from the forms of the equations in (5) in which it appears. In particular, the $L_rM$-equation can be written simply as $\partial _rM=4\pi r^2\rho$, which shows that M plays the role of an intrinsic mass that is determined by the amount of mass-energy in a sphere of radius r, also known as the Misner-Sharp mass [46, 47]. It is useful to note that [39] have shown that in spherically symmetric systems, M and r appear explicitly in the eigenvalues of the Weyl tensor, and r is also a measurable quantity; hence the name ‘physical’ coordinate. As they are both intrinsic (i.e. measurable) quantities, it is useful to construct our equations in terms of these variables.

The Eqs. (4)–(6) thus have clear physical interpretations and contain no residual gauge freedom (in non-vacuum regions). In particular, given an equation of state $p=p(\rho )$, and initial data in the form of the density $\rho (r,t_0)$ and the velocity $g_2(r,t_0)$, the future evolution of the system is fully determined. This is because $\rho$ determines p and M on a time slice and the definition of M then determines $g_1$. The equations for $L_rg_2$, $L_rp$ and $L_rf_1$ then determine the remaining information, namely F, G and $f_1$ respectively, on the time slice. Finally, the $L_t\rho$ equation and $L_tM$ equation (together with the definition of M) enable one to propagate $\rho$ and $g_2$, respectively, to the next time slice and the repeat the process. The equations can thus be implemented numerically as a simple set of first-order update equations. This approach was illustrated in [39, 42, 43].

An alternative way of solving the system of Eqs. (4)–(6), which was employed in [40, 41, 48], is not to impose an equation of state, but instead specify a form for $\rho (r,t)$ for all t or, equivalently, a form for M(r, t) followed by use of the $L_rM$. This method is used in Sect. 4. We merely note here that one may obtain the fluid pressure p(r, t) by first using the $L_tM$ equation to eliminate $f_1$ from the $L_rp$ equation, which then yields the ‘generalised Oppenheimer–Volkov’ equation [41]

$$\begin{aligned}&\partial _r p = - \left( \frac{\rho +p}{r}\right) \nonumber \\&\cdot \left( \frac{M+4\pi r^3p-\frac{1}{3}\varLambda r^3 + r^2 v\partial _r v - 4\pi r^4 (\rho +p) (\partial _t M)^{-1}v\partial _t v}{(1+v^2)r-2M-\frac{1}{3}\varLambda r^3} \right) . \end{aligned}$$

(8)

This equation is, in fact, valid for any spherically-symmetric perfect fluid system and reduces to the standard Oppenheimer–Volkov equation with a cosmological constant [49, 50] for a static spherically-symmetric system.

Finally, although the system of Eqs. (4)–(6) accommodates non-zero pressure, it is worth considering briefly the special case of a pressureless fluid. In this case, the $L_rp$ equation forces G to vanish, so the motion of the fluid particles becomes geodesic and the $L_rf_1$ equation forces $f_1=1$. Consequently, the components in the coordinate basis of the four-velocity of a fluid particle are $[v^\mu ] \equiv [\dot{t},\dot{r},\dot{\theta },\dot{\phi }]=[1,g_2,0,0]$, where dots denote differentiation with respect to the particle’s proper time $\tau$. Since $\dot{t}=1$, the coordinate time matches the proper time of all observers comoving with the fluid. Hence the Newtonian gauge is a synchronous one: a global ‘Newtonian’ time is recovered on which all comoving observers agree (provided all clocks are synchronised initially).³ Furthermore, combining the $L_tM$ equation and the definition of M yields $(\partial _t + g_2\partial _r)g_2=-M/r^2 + \frac{1}{3}\varLambda r$, which has the form of the Euler equation in Newtonian fluid dynamics (recalling that $g_2$ is the fluid velocity v). Finally, setting $\varLambda =0$ for a moment, the definition of M can itself be rearranged to give $\tfrac{1}{2}g_2-M/r = \frac{1}{2}(g_1^2-1)$, which is the Bernoulli equation for zero pressure and total (non-relativistic) energy per unit mass $\frac{1}{2}(g_1^2-1)$ (i.e. after subtraction of the rest-mass energy).

2.1 Application to Schwarzschild spacetime

As an illustration of our approach, we now apply it to the special case in which the matter source is concentrated at the single point $r=0$ and the cosmological constant vanishes (see also [39]). For such a solution, $\rho =p=0$ everywhere away from the origin and so that $M=\text{ constant }$. One can show that the Eqs. (4)–(6) reduce to an under-determined system of equations, such that additional gauge fixing is required to determine an explicit solution. This occurs because in the final part of our gauge-fixing procedure described above, one chooses the timelike unit Lorentz frame vector at each point to coincide with the fluid four-velocity at that point, which clearly cannot be performed in a vacuum region.

Nonetheless, one may instead choose the timelike unit frame vector to coincide with the four-velocity $\mathbf {u}$ of some radially-moving test particle (which need not necessarily be in free-fall), so that its components in the tetrad frame are $[\hat{u}^a] = [1,0,0,0]$ and hence in the coordinate basis one has $[u^\mu ] \equiv [\dot{t},\dot{r},\dot{\theta },\dot{\phi }]=[f_1,g_2,0,0]$, as previously. This ensures that our previous physical interpretations of the tetrad and spin-connection components still hold. It remains, however, to choose a particular class of radially-moving test particle, and the simplest and most natural choice is a radially free-falling particle that was released from rest at $r=\infty$. From the definition (6) of M (with $\varLambda \equiv 0$), one sees that $g_1$ corresponds to the total energy per unit rest mass of an infalling particle, and so for a particle released from rest at infinity one should adopt the gauge condition $g_1=1$. It is then a simple matter to obtain expressions for the remaining tetrad components and spin-connection coefficients. The resulting non-zero tetrad components are

$$\begin{aligned} f_1=1,\quad g_1=1, \quad g_2=-\frac{2M}{r}, \end{aligned}$$

(9)

and the spin-connection coefficients F and G read

$$\begin{aligned} F=\left( \frac{2M}{r}\right) ^{-1/2}\frac{M}{r^2},\quad G=0. \end{aligned}$$

(10)

We note that the condition $G=0$ is clearly consistent with the geodesic motion of the test particles.

The line-element (2) corresponding to the tetrad components (9) is given by

$$\begin{aligned} ds^2 = dt^2 - \left( dr + \sqrt{\frac{2M}{r}}\,dt\right) ^2 - r^2\,d\varOmega ^2, \end{aligned}$$

(11)

which we recognise as the Schwarzschild spacetime line-element expressed in terms of Painlevé–Gullstrand coordinates [51, 52]. This coordinate system has a number of desirable features. For example, the line-element is regular for all positive values of r and the spacelike hypersurfaces $t=\text{ constant }$ have Euclidean geometry. Moreover, from (9), the non-zero components of the four-velocity of a particle released from rest at infinity are immediately

$$\begin{aligned} \dot{t}=1,\quad \dot{r}=-\sqrt{\frac{2M}{r}}, \end{aligned}$$

(12)

and so we recover an essentially Newtonian description of the motion. In particular, we see that t coincides with the proper time of such particles.

Note that we can recover the standard form of the Schwarzschild line-element in Schwarzschild coordinates by choosing the preferred class of test particle to have fixed spatial coordinates, which leads to the tetrad components

$$\begin{aligned} f_1=\left( 1-\frac{2M}{r}\right) ^{-1/2},\quad g_1=\left( 1-\frac{2M}{r}\right) ^{1/2},\quad g_2=0, \end{aligned}$$

(13)

and the spin-connection coefficients

$$\begin{aligned} F=0,\quad G = \left( 1-\frac{2M}{r}\right) ^{-1/2}\frac{M}{r^2}. \end{aligned}$$

(14)

We note that $G\ne 0$ is consistent with non-geodesic motion of the test particles.

2.2 Application to FLRW spacetime

As a second illustration of our approach, we apply it to the special case of a homogeneous and isotropic spacetime, as assumed in cosmology. This corresponds to setting $\rho$ and p to be functions of t only, such that $M(r,t)=\tfrac{4}{3}\pi r^3 \rho$. One can show that the non-zero tetrad components are given by

$$\begin{aligned} f_1&=1,\nonumber \\ g^2_1&=1-kr^2\exp \left\{ {\textstyle -2\int ^t H(t')\,dt'}\right\} ,\nonumber \\ g_2&= rH(t), \end{aligned}$$

(15)

where k is an arbitrary constant of integration, and the spin-connection coefficients F and G are

$$\begin{aligned} F = H(t), \quad G=0. \end{aligned}$$

(16)

We note that the condition $G=0$ demonstrates that the fluid particles move geodesically, since there are no pressure gradients. Moreover, one can show

$$\begin{aligned} \partial _t\rho&=-3H(t)(\rho +p), \end{aligned}$$

(17)

$$\begin{aligned} \tfrac{8}{3}\pi \rho&=H^2(t) -\tfrac{1}{3}\varLambda +k\exp \left\{ {\textstyle -2\int ^t H(t')\,dt'}\right\} . \end{aligned}$$

(18)

One also obtains the further (although clearly not independent) dynamical equation

$$\begin{aligned} \partial _tH(t) + H^2(t)-\tfrac{1}{3}\varLambda = -\tfrac{4}{3}\pi (\rho +3p), \end{aligned}$$

(19)

which we recognise as the standard ‘acceleration’ cosmological field equation expressed in terms of the Hubble parameter H(t). Indeed, from (15), the non-zero components of the four-velocity of a fluid particle are immediately

$$\begin{aligned} \dot{t}=1,\quad \dot{r} = rH(t), \end{aligned}$$

(20)

which both verifies that t coincides with proper time of such particles and recovers Hubble’s law.

Thus, our approach has led us to work directly with H(t), which is an intrinsic and measurable quantity, rather than the more usual scale factor, which we will denote by S(t). Nonetheless, we can make contact with the latter simply by setting $H(t) \equiv \partial _t S(t)/S(t)$, in which case $g_1^2 = 1-kr^2/S^2(t)$. The line-element (2) corresponding to the tetrad components (15) then reads

$$\begin{aligned} ds^2 = dt^2 - \left( 1-\frac{kr^2}{S^2(t)}\right) ^{-1}\left[ dr-rH(t)\,dt\right] ^2-r^2\,d\varOmega ^2, \end{aligned}$$

(21)

and the dynamical equations (18) and (19) become

$$\begin{aligned} \frac{[\partial _t S(t)]^2 + k}{S^2(t)} -\tfrac{1}{3}\varLambda&= \tfrac{8}{3}\pi \rho , \end{aligned}$$

(22)

$$\begin{aligned} \frac{\partial ^2_tS(t)}{S(t)}-\tfrac{1}{3}\varLambda&= -\tfrac{4}{3}\pi (\rho +3p), \end{aligned}$$

(23)

which we recognise as Friedmann’s cosmological field equations in their standard form. Note that on defining the comoving radial coordinate $\hat{r} \equiv r/S(t)$, the line-element (21) takes the usual FLRW form.

3 Comparison with LTB model

In contrast to our tetrad-based approach, the LTB model [15,16,17] is based on the use of a comoving radial coordinate, which we denote by $\hat{r}$, and the assumption of a diagonal form for the metric. It is also usual to choose the time coordinate, which we denote by $\hat{t}$, to coincide with the proper time measured by observers comoving with the fluid, but for the moment we will consider the Lemaître metric [53], a slightly more general version of the LTB metric in which this requirement is not enforced. Thus, we consider a line element of the form

$$\begin{aligned} ds^2 = A^2d\hat{t}^2 - B^2d\hat{r}^2 - R^2 d\varOmega ^2, \end{aligned}$$

(24)

where, in general, A, B and R may be arbitrary functions of both $\hat{r}$ and $\hat{t}$. Note that the LTB metric corresponds to setting $A=1$.

We may understand the relationship between the line-element (24) and that given in (2), obtained using our tetrad-based approach, by performing a coordinate transformation that expresses the latter in terms of a comoving radial coordinate and brings it into diagonal form. We therefore consider the coordinate transformation

$$\begin{aligned} t=\hat{t}, \quad r=r(\hat{r},\hat{t}), \quad \text {where} \quad \frac{\partial r}{\partial \hat{t}}=\frac{g_2}{f_1}. \end{aligned}$$

(25)

Note that, although the time coordinates coincide, we still label the new one as $\hat{t}$, since the partial derivatives $\partial /\partial t$ and $\partial /\partial \hat{t}$ will, in general, be different because they hold fixed r and $\hat{r}$, respectively. One may verify that $\hat{r}$ is a comoving radial coordinate by recalling that the four-velocity components of a comoving observer in the Newtonian gauge are $[v^{\mu }]=(\dot{t}, \dot{r},\dot{\theta }, \dot{\phi }) = (f_1, g_2, 0,0)$, which transform under (25) into $[\hat{v}^{\mu }] =(\dot{\hat{t}},\dot{\hat{r}},\dot{\theta },\dot{\phi }) = (f_1,0,0,0)$. The physical nature of the transformation (25) may be further clarified by noting that

$$\begin{aligned} \frac{\partial }{\partial \hat{t}} = \frac{\partial t}{\partial \hat{t}} \frac{\partial }{\partial t} + \frac{\partial r}{\partial \hat{t}} \frac{\partial }{\partial r} = \frac{1}{f_1} \left( f_1 \frac{\partial }{\partial t} + g_2 \frac{\partial }{\partial r}\right) = \frac{1}{f_1} L_t, \end{aligned}$$

(26)

where $L_t$, defined in (3), is the derivative with respect to the proper time of a comoving observer; indeed this is consistent with our finding above that $\dot{\hat{t}}=f_1$. Since $L_t$ may be considered as a relativistic form of convective derivative, one may interpret the transformation (25) as moving from a Eulerian to a Lagrangian description of the fluid motion. Similarly, one finds that

$$\begin{aligned} \frac{\partial }{\partial \hat{r}} = \frac{1}{g_1} \frac{\partial r}{\partial \hat{r}} L_r, \end{aligned}$$

(27)

where $L_r$, also defined in (3), is the derivative with respect to the proper radial distance of a comoving observer.

Under the transformation (25) to a comoving radial coordinate, the line-element (2) takes the diagonal form

$$\begin{aligned} ds^2= \frac{1}{f_1^2}\,d\hat{t}^2 - \frac{1}{g_1^2} \left( \frac{\partial r}{\partial \hat{r}} \right) ^2 d\hat{r}^2 - r^2 d\varOmega ^2. \end{aligned}$$

(28)

One should first note that this has been achieved without having to specify $\partial r/\partial \hat{r}$; this demonstrates that the Lemaître (and hence LTB) metric (24) possesses a residual gauge freedom, in contrast to the line-element (2) (recall that the final gauge choice made in Sect. 2 leaves the form of (2) unchanged).

Comparing (24) and (28), one first identifies that $r=R(\hat{r},\hat{t})$ and hence the three non-zero tetrad components used in Sect. 2 are given by

$$\begin{aligned} f_1 = \frac{1}{A}, \quad g_1 = \frac{1}{B}\partial _{\hat{r}}R, \quad g_2 = \frac{1}{A}\partial _{\hat{t}}R, \end{aligned}$$

(29)

where the final result is obtained using (25). The expressions for the spin-connection coefficients F and G are obtained from the relations (4) and read

$$\begin{aligned} F = \frac{1}{AB}\partial _{\hat{t}}B, \quad G = \frac{1}{AB}\partial _{\hat{r}}A. \end{aligned}$$

(30)

Substituting the expressions (29) and (30) into the dynamical and continuity equations (5), one then obtains

$$\begin{aligned} \partial _{\hat{r}}p&= -\frac{(\rho + p)}{A}\partial _{\hat{r}}A, \end{aligned}$$

(31)

$$\begin{aligned} \partial _{\hat{r}}M&=4 \pi R^2 \rho \,\partial _{\hat{r}}R, \end{aligned}$$

(32)

$$\begin{aligned} \partial _{\hat{t}}\rho&= -\left( \rho + p \right) \left( \frac{2}{R}\partial _{\hat{t}}R + \frac{1}{B} \partial _{\hat{t}}B \right) , \end{aligned}$$

(33)

$$\begin{aligned} \partial _{\hat{t}}M&=-4 \pi R^2 p \,\partial _{\hat{t}}R, \end{aligned}$$

(34)

where the expression for M in (6) now becomes

$$\begin{aligned} \frac{2M}{R} = \frac{1}{A^2}\left( \partial _{\hat{t}}R\right) ^2- \frac{1}{B^2}\left( \partial _{\hat{r}}R \right) ^2 +1-\tfrac{1}{3}\varLambda R^2. \end{aligned}$$

(35)

The assumed form (24) of the line-element and the system of Eqs. (31)–(35) constitute a generalised form of the LTB model that can accommodate pressure and a non-zero cosmological constant. Nonetheless, unlike the tetrad-based approach, this model still possesses a gauge freedom, since $\partial _{\hat{r}}R$ remains arbitrary. Thus, to determine the evolution of the system, one must first choose a form for the function $R(\hat{r},\hat{t}_*)$ at some time $\hat{t}_*$ (usually given as an initial condition), which can sometimes be difficult to interpret physically.

To make contact with the standard LTB model, we may now set $A=1$ in the line-element (24), so that $\hat{t}$ coincides with the proper time measured by observers comoving with the fluid. Hence, like the Newtonian gauge, the standard LTB model employs a synchronous coordinate system. In terms of the tetrad components (29) and spin-connection coefficients (30), setting $A=1$ corresponds to setting $f_1=1$ and $G=0$, and hence (26) shows that the operators $\partial _{\hat{t}}$ and $L_t$ then coincide. Thus, from the $L_tg_1$ equation in (4) one finds that $g_1=g_1(\hat{r})$ is a function only of $\hat{r}$. Using the expression for $g_1$ in (29) and adopting the standard notation used in LTB models, we therefore define the function $E(\hat{r})$ by

$$\begin{aligned} 1+2E(\hat{r}) \equiv \frac{1}{B^2}(\partial _{\hat{r}}R)^2, \end{aligned}$$

(36)

which we may choose arbitrarily provided that $E(\hat{r}) > -\tfrac{1}{2}$. It is also immediately clear from (31) that setting $A=1$ requires the pressure gradient to vanish. Thus, the standard LTB line-element can at best accommodate a fluid with a non-zero homogeneous pressure. It is usual, however, to assume simply that the fluid is pressureless, in which case (34) shows that $M=M(\hat{r})$ is a function only of $\hat{r}$. Given our earlier interpretation of M in the tetrad-based approach, one may thus verify the usual interpretation of $M(\hat{r})$ in the LTB model as the Misner-Sharp mass, which is naturally time-independent in the absence of pressure.

3.1 Application to Schwarzschild spacetime

As an illustration of the LTB model, and in particular to compare it with the tetrad-based approach, we now apply it to the same physical situation as we considered in Sect. 2.1, namely that of a matter source concentrated into a single point and a vanishing cosmological constant. As previously, for such a solution, $\rho =p=0$ everywhere away from the point mass, and so (34) implies that $M=\text{ constant }$. Once again, the remaining system of equations is under-determined, and so some gauge-fixing is required. First we must choose a form for the arbitrary function $E(\hat{r})$. Similar to the approach adopted in Sect. 2.1, we may base our choice on some class of radially-moving test particle and, once again, the most natural choice is a radially free-falling particle released from rest at infinity. From the definition (36), we see that the choice of $g_1=1$ in our tetrad-based approach is equivalent to setting $E(\hat{r})=0$, which corresponds to the particle having zero energy (after subtraction of its rest mass energy).

One can show that the LTB equations can be then integrated to obtain $\tfrac{2}{3}R^{3/2}=-(2M)^{1/2}[\hat{t}-\hat{t}_b(\hat{r})]$, where the “bang-time” $\hat{t}_{\mathrm{b}}(\hat{r})$ may be an arbitrary function of $\hat{r}$, but is usually chosen such that $R(\hat{r},\hat{t}_{\mathrm{b}}(\hat{r}))=0$, which in this case requires $\hat{t}_{\mathrm{b}}(\hat{r})=\hat{r}$. Thus, after this additional gauge-fixing, which was not required in the tetrad based approach, one obtains

$$\begin{aligned} ds^2 = d\hat{t}^2 - \tfrac{4}{9}\left[ \frac{9M}{2(\hat{r}-\hat{t})}\right] ^{2/3}\,d\hat{r}^2- \left[ \frac{9M}{2}(\hat{r}-\hat{t})^2\right] ^{2/3}\,d\varOmega ^2, \end{aligned}$$

(37)

which is the line-element for the Schwarzschild spacetime expressed in Lemaître coordinates [15].

It is interesting that, although the tetrad-based approach and the LTB model both employ synchronous time coordinates and are based on the trajectories of radially infalling particles released from rest at infinity, the two methods naturally lead to the very different line-elements (11) and (37). This occurs because of the use of a ‘physical’ radial coordinate in the former, whereas the latter employs a comoving radial coordinate, and also the requirement that the LTB line-element be diagonal. In the authors’ opinion, the former line-element, expressed in Painlevé–Gullstrand coordinates, is the more easily interpreted physically.

3.2 Application to FLRW spacetime

As an second illustration of the LTB model, we now apply it to the special case of a homogeneous and isotropic spacetime, as considered in Sect. 2.2 using the tetrad-based approach. As before, this corresponds to setting $\rho$ to be a function of $\hat{t}$ only, but for the LTB model we are limited to considering only pressureless fluids and so $p=0$. In contrast to the tetrad-based approach, one must begin by making a gauge choice for the form for $M(\hat{r})$. This is most naturally achieved by introducing the scale factor $S(\hat{t})$ at the outset, such that $\rho (\hat{t})=\rho _0[S_0/S(\hat{t})]^3$, where $\rho _0 \equiv \rho (\hat{t}_0)$ and $S_0 \equiv S(\hat{t}_0)$ are defined at some cosmic time $\hat{t}=\hat{t}_0$, usually taken in cosmology to be the current epoch. Keeping in mind the physical interpretation of $M(\hat{r})$, it is then simplest to assume the form $M(\hat{r})=\tfrac{4}{3}\pi \rho _0S_0^3\hat{r}^3$. Once we have made this gauge choice, we find that $R = S(\hat{t})\hat{r}$ and $E(\hat{r})=-\tfrac{1}{2}k\hat{r}^2$, where k is a constant. Thus the line-element (24) (with $A=1$) takes the usual FLRW form

$$\begin{aligned} ds^2 = dt^2 - S^2(t)\left( \frac{d\hat{r}^2}{1-k\hat{r}^2}+\hat{r}^2\,d\varOmega ^2\right) . \end{aligned}$$

(38)

Moreover, the remaining LTB equations (36) and (34) then yield the standard Friedmann equation and cosmological continuity equation, respectively, namely

$$\begin{aligned} \frac{[\partial _{\hat{t}} S(\hat{t})]^2 + k}{S^2(\hat{t})} -\tfrac{1}{3}\varLambda&= \tfrac{8}{3}\pi \rho , \end{aligned}$$

(39)

$$\begin{aligned} \partial _{\hat{t}}\rho&=-3H(\hat{t})\rho , \end{aligned}$$

(40)

where we have defined the Hubble parameter $H(\hat{t})\equiv \partial _{\hat{t}}S(\hat{t})/S(\hat{t})$.

Thus, we see that the LTB model has led us directly to working in terms of the scale factor, in contrast to the tetrad-based approach used in Sect. 2.2, which led naturally to the Hubble parameter, which is a directly measurable quantity. Moreover, considerable gauge-fixing was required in the LTB model to obtain a definite form for the solution, whereas this was unnecessary in the tetrad-based approach.

4 Generalised Swiss cheese model

We now apply our tetrad-based approach to a generalised form of the Swiss cheese model. In its classic form, the Swiss cheese model consists of an exterior expanding FLRW universe, albeit pressureless, in which a pressureless spherical object is embedded and surrounded by a ‘compensating void’ that itself expands into the background and ensures that there is no net gravitational effect on the exterior universe. Such models were employed in some of the earliest attempts to describe non-linear cosmological inhomogeneities [54,55,56,57,58], since they have the advantage that analytical calculations can be performed, and compensation ensures observations in the exterior region can be modelled unambiguously. They have also been used in more recent attempts to characterise effects of inhomogeneities on cosmological observations, such as luminosity distance and perceived dark energy [59,60,61,62,63,64,65,66,67,68,69,70]. Nonetheless, the matter and velocity distributions are clearly unrealistic.

As mentioned in the Introduction, more realistic models can be constructed by working with continuous density and velocity profiles, while still restricting to spherical symmetry and ignoring pressure. Previous work using LTB models [71, 72] has usually ignored compensation, and this can lead to subtleties in modelling observations in the exterior region, since it is not described by a homogeneous FLRW cosmology, such as a net gravitational effect seen in the ISW effect [38, 73]. The initial density and velocity profiles must be carefully chosen so that streamline crossing is avoided [42, 43]. Otherwise, shock fronts form and one must include pressure to produce a realistic model. Compensation in tetrad formalism is discussed in [42, 43] and in the LTB formalism in [74, 75].

In this section, however, our primary focus is not the modelling of realistic cosmological inhomogeneities or the prediction of observational effects in the exterior region. Rather, we wish merely to extend the analysis presented in [41] (hereinafter NLH3) by applying our tetrad-based method to a generalised form of Swiss cheese model, in which we allow the fluid in the interior and exterior regions to support pressure, in general, and do not demand that the interior region be compensated. Aside from intellectual curiosity, the motivations for this study are two-fold: we first wish to verify that Birkhoff’s theorem holds in the vacuum region, the usual interpretation of which has recently been brought into question for related systems [44]; and, second, we wish to consider the validity of the theoretical arguments that underpin the $R_{\mathrm{h}}=ct$ cosmological model [45, 76, 77], which has recently received considerable attention [78,79,80]. These investigations are presented, respectively, in Sects. 5 and 6 below.

As discussed in Sect. 2, instead of imposing an equation of state, $p=p(\rho )$, we solve the system of Eqs. (4)–(6) by specify a form for $\rho (r,t)$ for all t or, equivalently, a form for M(r, t) followed by use of the $L_rM$. In general, the remaining equations need to be solved as a set of coupled PDEs. Nonetheless, as shown in [40, 41, 48], if $\rho (r,t)$ is piecewise uniform in r, then one may combine the $L_t\rho$, $L_tM$ and $L_rM$ equations to obtain an ODE in r that may be solved to obtain an expression for the fluid velocity $g_2(r,t)$ and hence F(r, t), albeit with each containing a time-dependent ‘constant’ of integration, and the definition of M then determines $g_1(r,t)$.

One may obtain the fluid pressure p(r, t) by using the ‘generalised Oppenheimer–Volkov’ equation (8), which requires the imposition of a boundary condition on the pressure at some radius. One may then complete the solution either by obtaining $f_1(r,t)$ from the $L_t\rho$ equation and hence G(r, t) from any other equation that contains it, or by obtaining G(r, t) from the $L_rp$ equation and then $f_1(r,t)$ from the $L_rf_1$ equation.

Fig. 1

Generalised Swiss cheese model a spherical interior region of uniform density $\rho _{\mathrm{i}}(t)$ and radius a(t) is surrounded by a vacuum region of radius b(t), which itself resides in an exterior region with uniform density $\rho _{\mathrm{e}}(t)$. The rates of expansion of the interior, vacuum and exterior regions are characterized by the ‘Hubble parameters’ $H_{\mathrm{i}}(t)$, $H_{\mathrm{v}}(t)$ and $H_{\mathrm{e}}(t)$, respectively. In general, the fluid can support pressure and the interior region need not be compensated

4.1 Model specification

The generalised Swiss cheese model is illustrated in Fig. 1 and consists of a spherical interior region of uniform density $\rho _{\mathrm{i}}(t)$ and radius a(t) surrounded by a vacuum region of radius b(t), which itself resides in an exterior region with uniform density $\rho _{\mathrm{e}}(t)$. The rates of expansion of the interior, vacuum and exterior regions are characterized by the ‘Hubble parameters’ $H_{\mathrm{i}}(t)$, $H_{\mathrm{v}}(t)$ and $H_{\mathrm{e}}(t)$, respectively (the definition of $H_{\mathrm{v}}(t)$ is discussed below). These functions are free for us to choose, and together with M(r, t) and initial conditions, completely specify the evolution of the system. As we show later on, these ‘Hubble parameters’ are, in fact, equal to the covariant Hubble scalar in both the interior and exterior regions. In general, the interior region need not be compensated and the fluid in both the interior and exterior regions can support pressure.

From the figure, we may write down an expression for the total mass-energy M(r, t) contained within a sphere of physical radius r at time t. It is clear that

$$\begin{aligned} M= {\left\{ \begin{array}{ll} \frac{4}{3} \pi \rho _{\mathrm{i}}(t)r^3, &{}\quad r\le a(t),\\ \frac{4}{3} \pi \rho _{\mathrm{i}}(t)a(t)^3 \equiv M_0, &{}\quad a(t) \le r\le b(t),\\ \frac{4}{3} \pi \rho _{\mathrm{e}}(t)r^3 + m(t), &{}\quad r \ge b(t), \end{array}\right. } \end{aligned}$$

(41)

where $M_0$ is a constant and $m(t)= M_0 - \frac{4}{3} \pi \rho _{\mathrm{e}}(t) b(t)^3$ is the mass contained within b(t) at time t, in excess of that which would be present due to the exterior background alone. For a compensated interior region, one thus has $m(t) \equiv 0$. We note that the system considered in NLH3 corresponds to setting $b(t)=a(t)$, so that there is no vacuum region.

As we will show below, in the general case where the fluid supports pressure, to determine the dynamical evolution of the system completely one must specify the internal and external Hubble parameters $H_{\mathrm{i}}(t)$ and $H_{\mathrm{e}}(t)$, together with the evolution a(t) and b(t) of the two boundaries (and the density $\rho _{*}\equiv \rho _{\mathrm{i}}(t_*)$ of the interior region at some reference time $t=t_*$). Typically, one should take $H_{\mathrm{e}}(t)$ to correspond to some expanding exterior universe of interest, but $H_{\mathrm{i}}(t)$, a(t) and b(t) can, in principle, have any form.⁴ This follows both from the presence of the vacuum region and from allowing the relationship between the fluid pressure and density to be arbitrary, since then the interplay between pressure and gravity may allow expansion or contraction of the interior and vacuum regions at any rate. This freedom would disappear, however, if one imposed an equation of state on the fluid. In particular, in the special case of a pressureless fluid, a(t) is straightforwardly determined from $H_{\mathrm{i}}(t)$ (and the radius $a_*\equiv a(t_*)$ at some reference time $t=t_*$).

We note that by leaving $H_{\mathrm{i}}(t)$ and $H_{\mathrm{e}}(t)$ free to choose, we are treating the system as being composed of a mathematical fluid, that is intended to mimic the kinematical evolution (if not the physics) of a combination of baryonic gas and dark matter, having a single effective density and a single effective pressure required for stability (for more details, see [48]). This results in an effective ‘equation’ of state which depends on both r and t. Choosing the Hubble parameters and specifying the mass-energy M(r, t) means that we can solve for p(r, t) using the generalised Oppenheimer–Volkov equation (8). Hence the effective ‘equation of state’ is then determined. Treating the fluid as a single mathematical fluid avoids the complication of calculating the non-linear evolution of multi-fluid systems, whereby one would separate the fluid in each region into its baryonic and dark matter components.

4.2 Boundary conditions

Any spatial surface at which the density is discontinuous, and which may in general be moving, will trace out a 3-dimensional (timelike) hypersurface $\varSigma$ in spacetime on which the solution must satisfy the Israel junction conditions [81, 82]. If $\hat{n}_\mu$ are the covariant components of the unit (spacelike) normal to $\varSigma$, pointing from the inside to the outside, then the Israel junction conditions require both of the induced metric $h_{\mu \nu }=g_{\mu \nu }+\hat{n}_\mu \hat{n}_\mu$ and the extrinsic curvature $K_{\alpha \beta } = {h_\alpha }^\mu {h_\beta }^\nu \nabla _\mu \hat{n}_\nu$ to agree on $\varSigma$.

For the model illustrated in Fig. 1, two such hypersurfaces are defined by $\varSigma (t,r) \equiv r-x(t) = 0$, where x(t) can equal either a(t) or b(t). As discussed in [41], the components $\hat{n}_\mu$ are given by

$$\begin{aligned}{}[\hat{n}_\mu ] = \frac{[-\partial _t x, 1, 0, 0]}{|f_1^2 \partial _t x-2f_1 g_1 \partial _t x + g_2^2-g_1^2|^{1/2}}, \end{aligned}$$

(42)

where $\partial _t x \equiv dx(t)/dt$; one may readily verify that $\hat{n}_\mu \hat{n}^\mu = -1$, as required. One sees immediately that, for the induced metric to be agree across the boundary x(t), one requires all three non-zero tetrad components $f_1$, $g_1$ and $g_2$ to be continuous there.

Recalling that $g_2$ is the rate of change of the r coordinate of a fluid particle with respect to its proper time, and can thus be considered as the fluid velocity, the physical interpretation of the continuity of $g_2$ is that matter does not cross the boundary x(t) in either direction. This is consistent with the boundary x(t) comoving with the fluid, so that the situation depicted in Fig. 1 does indeed hold at all times. It does not imply, however, that M(x(t), t) is constant, since this quantity denotes the total energy within x(t), which may change as x(t) evolves, as is clear from the $L_tM$ and $L_rM$ equations in (5). Moreover, since $L_t$ corresponds to the derivative with respect to the proper time of an observer comoving with the fluid, then one requires

$$\begin{aligned} L_t x(t) = g_2(x(t),t), \end{aligned}$$

(43)

where $L_t$ is evaluated at the boundary x(t). Thus, on the hypersurface $\varSigma$, one has $dx(t)/dt = g_2/f_1$ and the expression (42) simplifies to

$$\begin{aligned} {[}\hat{n}_\mu ] = \frac{1}{g_1}[-g_2/f_1, 1, 0, 0]. \end{aligned}$$

(44)

After a long but straightforward calculation, one then finds that the only non-zero components of the extrinsic curvature of $\varSigma$ are⁵

$$\begin{aligned} K_{00} = \frac{g_1}{f_1^3}\partial _r f_1,\quad K_{11} = g_1r,\quad K_{22} = g_1r \sin ^2\theta . \end{aligned}$$

(45)

Since the first Israel junction condition requires $f_1$, $g_1$ and $g_2$ all to be continuous at the boundary x(t), then the second junction condition requires only that, in addition, $\partial _r f_1$ is continuous there.

The above junction conditions have consequences for the continuity of other variables of interest. In particular, from the $L_rf_1$ equation in (4), one has $G = -(g_1/f_1)\partial _r f_1$, which must therefore also be continuous at the boundary. Moreover, the $L_rp$ equation in (5) and the continuity of $g_1$ and G imply that the pressure p is also continuous across the boundary, although its radial derivative, in general, has a step there.

Finally, we also adopt the boundary condition at large r that all physical quantities tend to those of the exterior cosmology. For spatially-flat and open universes, this corresponds to the limit $r\rightarrow \infty$, whereas for a closed universe one must instead consider the limit $x(t) \ll r < S(t)$, where S(t) is the universal scale factor which also corresponds to the curvature scale for a closed universe. In each case, we require the line-element (2) to tend at large r to the corresponding FLRW line-element (21) with $H(t) = H_{\mathrm{e}}(t)$. Thus, for large r, one requires

$$\begin{aligned} f_1 \rightarrow 1,\quad g_1 \rightarrow \sqrt{1-\frac{kr^2}{S^2(t)}},\quad g_2 \rightarrow rH_{\mathrm{e}}(t). \end{aligned}$$

(46)

4.3 Interior and exterior regions

From (41), one sees that the forms for M in the interior and exterior regions are the same as the model considered in NLH3, albeit with a different definition of m(t). Moreover, the same boundary conditions (46) apply at large r. Therefore, many of the equations derived in NLH3 remain valid.

Specifically, in the interior region, the non-zero tetrad components are again given by

$$\begin{aligned} f_{1,\mathrm{i}}&= -\frac{3H_{\mathrm{i}}(t)\left( \rho _{\mathrm{i}}(t)+p_{\mathrm{i}} \right) }{\rho _{\mathrm{i}}'(t)}, \end{aligned}$$

(47)

$$\begin{aligned} g_{1,\mathrm{i}}&= \sqrt{1+r^{2} \left( H_{\mathrm{i}}^{2}(t)-\tfrac{8 }{3} \pi \rho _{\mathrm{i}}(t)- \tfrac{1}{3} \varLambda \right) }, \end{aligned}$$

(48)

$$\begin{aligned} g_{2,\mathrm{i}}&= rH_{\mathrm{i}}(t), \end{aligned}$$

(49)

where, following NLH3, a prime denotes differentiation with respect to t. In order to evaluate the above expressions for $f_{1,\mathrm{i}}$ and $g_{1,\mathrm{i}}$, one requires forms for $\rho _{\mathrm{i}}(t)$ and $p_{\mathrm{i}}$. Substituting the above expression for the fluid velocity $g_{2,\mathrm{i}}$ and the enclosed mass $M=\tfrac{4\pi }{3}\rho _{\mathrm{i}}(t)r^3$ from (41) into the generalised Oppenheimer–Volkov equation (8), and integrating, will yield an (integral) expression for $p_{\mathrm{i}}$ in terms of $H_{\mathrm{i}}(t)$ and $\rho _{\mathrm{i}}(t)$, after imposing the condition that the pressure is continuous across the boundary a(t) and hence vanishes there. Thus, it only remains to determine $\rho _{\mathrm{i}}(t)$, which is straightforwardly obtained for a given boundary evolution a(t) by recalling that $M_0 \equiv \frac{4\pi }{3}\rho _{\mathrm{i}}(t)a^3(t)$ is a constant. In the special case of a pressureless fluid, it is worth noting that one immediately has $f_{1,\mathrm{i}}=1$ and so (47) can be integrated to obtain $\rho _{\mathrm{i}}(t)$, which then determines a(t).

For the exterior region, the non-zero tetrad elements are given by

$$\begin{aligned} f_{1,\mathrm{e}}&=-\frac{3H_{\mathrm{e}}(t)\left( \rho _{\mathrm{e}}(t)+p_{\mathrm{e}}\right) }{\rho _{\mathrm{e}}'(t)}, \end{aligned}$$

(50)

$$\begin{aligned} g_{1,\mathrm{e}}^2&=1- \frac{2m(t)}{r} + \left( H_{\mathrm{e}}(t)^{2}-\tfrac{8}{3} \pi \rho _{\mathrm{e}}(t)-\tfrac{1}{3}\varLambda \right) r^2 \nonumber \\&\quad + \frac{9H_{\mathrm{e}}^2(t)m'(t)}{16\pi ^2 \rho _{\mathrm{e}}'^2(t)r^4} \left( \tfrac{8}{3}\pi \rho _{\mathrm{e}}'(t) r^3 + m'(t) \right) ,\end{aligned}$$

(51)

$$\begin{aligned} g_{2,\mathrm{e}}&=r H_{\mathrm{e}}(t) + \frac{3m'(t)H_{\mathrm{e}}(t)}{4 \pi r^{2}\rho _{\mathrm{e}}'(t)}. \end{aligned}$$

(52)

In order to evaluate the above expressions, one requires forms for $p_{\mathrm{e}}$, $\rho _{\mathrm{e}}(t)$ and b(t). Substituting the expressions for M and $g_{2,\mathrm{e}}$ into the generalised Oppenheimer–Volkov equation (8), integrating and imposing the condition that the pressure is continuous across the boundary b(t) and hence vanishes there, will yield an (integral) expression for $p_{\mathrm{e}}$ in terms of $\rho _{\mathrm{e}}(t)$, $H_{\mathrm{e}}(t)$, b(t) and the (in general) time-dependent uniform fluid pressure $p_{\infty }(t)$ at large r corresponding to the external cosmological model. One is free to specify $H_{\mathrm{e}}(t)$, b(t) and $p_{\infty }(t)$, and the function $\rho _{\mathrm{e}}(t)$ may be determined from the following equations from NLH3 which remain valid in the exterior region:

$$\begin{aligned} \rho _{\mathrm{e}}'(t) + 3H_{\mathrm{e}}(t) \left( \rho _{\mathrm{e}}(t) + p_{\infty }(t) \right)&= 0, \end{aligned}$$

(53)

$$\begin{aligned} H_{\mathrm{e}}^{2}(t)-\tfrac{8 }{3} \pi \rho _{\mathrm{e}}(t)- \tfrac{1}{3}\varLambda&= - \frac{k}{R^2(t)}. \end{aligned}$$

(54)

We recognise (53) and (54) as the standard cosmological fluid evolution equation and the Friedmann equation, respectively. Moreover, as in NLH3, these can be combined in the usual manner to yield the dynamical cosmological field equation

$$\begin{aligned} H'_{\mathrm{e}}(t) + H_{\mathrm{e}}^2(t) -\tfrac{1}{3}\varLambda = -\tfrac{4}{3}\pi (\rho _{\mathrm{e}}(t)+3p_\infty (t)), \end{aligned}$$

(55)

which thus provides an expression for $\rho _{\mathrm{e}}(t)$ in terms of $H_{\mathrm{e}}(t)$ and $p_\infty (t)$.

We are free to choose the boundary evolution b(t), and it is most convenient to do this by defining the ‘vacuum Hubble parameter’ $H_{\mathrm{v}}(t)$, such that

$$\begin{aligned} g_{2,\mathrm{e}}(b(t),t)= b(t)H_{\mathrm{v}}(t). \end{aligned}$$

(56)

Equating the above expression with (52) evaluated on the boundary b(t), one obtains

$$\begin{aligned} \frac{b'(t)}{b(t)}= -\frac{H_{\mathrm{v}}(t) \rho _{\mathrm{e}}'(t)}{3\rho _{\mathrm{e}}(t) H_{\mathrm{e}}(t)}. \end{aligned}$$

(57)

This then allows one to write (52) in the elegant form

$$\begin{aligned} g_{2,\mathrm{e}}=rH_{\mathrm{e}}(t) - \frac{b^3(t)}{r^2} \left( H_{\mathrm{e}}(t)-H_{\mathrm{v}}(t) \right) . \end{aligned}$$

(58)

In a similar manner, one may write the expression (51) as

$$\begin{aligned} g^2_{1,\mathrm{e}}&=1-\frac{2m}{r} + (H_{\mathrm{e}}^2-\tfrac{8}{3}\pi \rho _{\mathrm{e}} - \tfrac{1}{3}\varLambda )r^2 \nonumber \\&\quad + \frac{b^3}{r} (H_{\mathrm{v}} - H_{\mathrm{e}}) \left[ 2H_{\mathrm{e}} + \frac{b^3}{r^3} (H_{\mathrm{v}} - H_{\mathrm{e}}) \right] , \end{aligned}$$

(59)

where we have momentarily suppressed t-dependencies for brevity. It is worth noting that, for the special case of a pressureless fluid, one immediately has $p_{\mathrm{e}}=0$ and $f_{1,\mathrm{e}}=1$, so (57) becomes simply $b'(t)/b(t) = -H_{\mathrm{v}}(t)$.

4.4 Hubble scalar and shear in the interior and exterior regions

The fluid velocity covariant derivative can be split into parts with specific symmetry properties [83, 84]. The decomposition is given by (from equation (4.17) in [83], adapted to our metric signature)

$$\begin{aligned} \nabla _{\nu } v_{\mu } = \omega _{\mu \nu }+\sigma _{\mu \nu }+\tfrac{1}{3} \theta h_{\mu \nu }+\dot{v}_{\mu } v_{\nu }, \end{aligned}$$

(60)

where $\omega _{\mu \nu }$ is the vorticity tensor, $\sigma _{\mu \nu }$ is the shear tensor, $h_{\mu \nu }$ is the projection tensor into the 3D subspace orthogonal to the fluid velocity, and the volume expansion scalar, $\theta$, is defined as

$$\begin{aligned} \theta = \nabla _{\mu } {v^{\mu }}. \end{aligned}$$

(61)

Hence, the Hubble scalar is defined as

$$\begin{aligned} H_s = \tfrac{1}{3} \theta . \end{aligned}$$

(62)

The shear tensor is defined as the traceless component of the ‘fully projected’ part of the symmetric piece of $\nabla _{\nu } v_{\mu }$. Specifically we define

$$\begin{aligned} \theta _{\mu \nu }={h_{\mu }}^\rho {h_\nu }^\tau \nabla _{( \tau }v_{\rho )}, \end{aligned}$$

(63)

such that the shear tensor is given by

$$\begin{aligned} \sigma _{\mu \nu }=\theta _{\mu \nu }- \tfrac{1}{3} h_{\mu \nu }\theta . \end{aligned}$$

(64)

The final quantity of interest is the relativistic 4-acceleration vector

$$\begin{aligned} \dot{v}^{\mu }=a^{\mu } = v^{\nu } \nabla _{\nu } {v^{\mu }}, \end{aligned}$$

(65)

which represents the degree to which matter moves under forces other than those of gravity (see for example, Section 2.1 in [84]).

We now consider the values of these quantities in the interior and exterior regions of our spherically symmetric solutions.

Since the fluid 4-velocity components, in a $(t,r,\theta , \phi )$ coordinate system, are given by $v^\mu =\frac{d x^\mu }{d\tau }=(f_1,g_2,0,0)$ (where $g_2$ is the fluid 3-velocity), the Hubble scalar (62) in terms of tetrad components is given by

$$\begin{aligned} H_{s} = \tfrac{1}{3} \left( \frac{\partial g_2}{\partial r} + 2 \frac{g_2}{r} \right) . \end{aligned}$$

(66)

In fact, in both the interior and exterior regions, the Hubble scalar simply reduces to the interior and exterior Hubble parameters respectively, despite the 3-velocity field deviating from the Hubble flow. That this occurs in the interior region is unsurprising, since Eq. (49) shows that the fluid 3-velocity here coincides with a pure Hubble flow, $rH_{\mathrm{i}}(t)$. In the exterior region, one again has $H_s(t) =H_e(t)$ despite the fluid 3-velocity $g_2$ deviating from a pure Hubble flow, $rH_{\mathrm{e}}(t)$ (see Eq. (58)). This occurs because the deviation is a function of time divided by $r^2$, for which the contribution to the 4-divergence $\nabla _{\mu } v^{\mu }$ vanishes.

We can construct the shear tensor using Eq. (64) above. If we denote $S=\frac{1}{3}\left( \frac{\partial g_2}{\partial r} - \frac{g_2}{r}\right)$, one can find using Eq. (64) that the eigenvalues of the shear tensor are 0 in the t direction, 2S in the r direction and $-S$ in the $\theta$ and $\phi$ directions. We note this is traceless as required for a shear tensor.

This shows a nice complementarity to what we just found for the Hubble scalar, since here the part of $g_2$ corresponding to the Hubble flow gives zero shear, as expected, whilst for the exterior, the deviation $- \frac{b^3(t)}{r^2} \left( H_{\mathrm{e}}(t)-H_{\mathrm{v}}(t) \right)$, as given in Eq. (58), gives us the tangential shear eigenvalue $-S$. Hence the model studied here, at least in the exterior region, is different from those studied by [85], where the fluid is assumed to be wholly shear-free.

The fact a spherically symmetric fluid can have a Hubble scalar which is everywhere the same as the Hubble parameter at infinity (where there is just a cosmological flow), but nevertheless has non-zero shear (tending to zero at infinity), is perhaps worthy of further comment. Specifically, such a fluid would have to obey the irrotational version of one of the constraint equations which can be derived from the Ricci identity as applied to the velocity 4-vector. To discuss this briefly, we will use the notation employed in [86], which generalises the 1+3 covariant approach to fluid dynamics of [84] to the context of fluids with intrinsic spin, but is convenient here since it uses the same $(+,-,-,-)$ metric as the present work.

The Ricci identity from [86] is

$$\begin{aligned} 2 \nabla _{[\mu }\nabla _{\nu ]}v_\rho = {R_{[\mu \nu ]\rho }}^\lambda v_\lambda , \end{aligned}$$

(67)

and by taking an antisymmetric trace-free part, employing the Einstein equations and (for current purposes) setting the spin and vorticity to zero, we can derive the equation

$$\begin{aligned} D_\lambda \sigma _\mu ^\lambda -{\textstyle \frac{2}{3}}D_\mu \theta =0, \end{aligned}$$

(68)

where $D_\lambda$ is the fully projected covariant derivative, which in this case would satisfy

$$\begin{aligned} D_\mu \theta ={h^\epsilon }_\mu \nabla _\epsilon \theta . \end{aligned}$$

(69)

Evaluating this constraint equation for the shear tensor and volume expansion scalar found above, we find that there is a non-zero entry for $\mu =r$, given (as a general function of the tetrad components) by

$$\begin{aligned} \left. \left( D_\lambda \sigma _\mu ^\lambda -{\textstyle \frac{2}{3}}D_\mu \theta \right) \right| _{\mu =r} \propto f_1^2 \frac{\partial g_1}{\partial t} + f_1 g_2 \frac{\partial g_1}{\partial r} + g_1 g_2 \frac{\partial f_1}{\partial r}. \end{aligned}$$

(70)

This looks as though there is a problem, but in fact the RHS here is proportional to the Einstein tensor entry $G_{tr}$, which due to our choice of fluid velocity vector, has to vanish (this can be confirmed independently via the explicit solutions for these quantities we have given in each region, including the external one). Thus our results for the shear and expansion factor, and in particular the fact that the expansion parameter can correspond to what one would have for a uniform Hubble flow, whilst the fluid still has non-zero shear, are fully consistent with the Ricci identity constraint on the shear divergence.

Finally, we note that the 4-acceleration $a^\mu =v^\nu \nabla _\nu v^\mu$ simply evaluates to a radial vector with magnitude G, as already discussed in Sect. 2.

4.5 Vacuum region

In the vacuum region, one has $\rho =p=0$ and so $L_rM=0$ and $L_tM=0$, which together imply M is a constant, which we have denoted by $M_0$. As we found in our discussion of the Schwarzschild spacetime in Sect. 2.1, in a vacuum region the system of Eqs. (4)–(6) reduces just to the relationships (4) between the tetrad and spin-connection components and the definition of $M (= M_0)$ in (6), from which one finds that the quantity

$$\begin{aligned} g_1^2- g_2^2 = 1-\frac{2 M_0}{r} - \tfrac{1}{3}\varLambda r^2 \equiv \alpha (r) \end{aligned}$$

(71)

is a function of r only. No further equations yield new information, and one thus has an under-determined system of equations that requires additional gauge-fixing to determine an explicit solution.

This occurs because in a vacuum region one clearly cannot choose the timelike unit Lorentz frame vector at each point to coincide with the fluid four-velocity at that point. As we did for the Schwarzschild spacetime, however, one may instead choose the timelike unit frame vector to coincide with the four-velocity $\mathbf {u}$ of some radially-moving test particle (which need not necessarily be in free-fall), so that its components in the tetrad frame are $[\hat{u}^a] = [1,0,0,0]$ and hence in the coordinate basis one has $[u^\mu ] \equiv [\dot{t},\dot{r},\dot{\theta },\dot{\phi }]=[f_{1,\mathrm{v}},g_{2,\mathrm{v}},0,0]$, as previously. Moreover, this ensures that our previous physical interpretations of the tetrad and spin-connection components still hold.

Unlike in the Schwarzschild spacetime, however, there is no simplest or most natural choice for the class of radially-moving test particle to use. All one requires is that the boundary conditions discussed in Sect. 4.2 hold at each boundary a(t) and b(t). It is most convenient to begin by choosing $g_{2,\mathrm{v}} = v(r,t)$, where v may be an arbitrary function satisfying the boundary conditions $v(a(t),t)=g_{2,\mathrm{i}}(a(t),t)=a(t)H_{\mathrm{i}}(t)$ and $v(b(t),t)=g_{2,\mathrm{e}}(b(t),t)=b(t)H_{\mathrm{v}}(t)$. Then $g_{1,\mathrm{v}}$ is easily found from (71) and is also continuous at both boundaries. Finally, eliminating G between the $L_rf_1$ and $L_t g_1$ equations in (4) gives the general relation

$$\begin{aligned} \partial _r(f_1g_1)+\frac{f_1^2}{g_2}\partial _tg_1=0, \end{aligned}$$

(72)

and using (71) to substitute for $g_1$, one then finds

$$\begin{aligned} \partial _r\left( f_{1,\mathrm{v}}\sqrt{\alpha (r)+v^2}\right) + f_{1,\mathrm{v}}^2 \frac{\partial _t v}{\sqrt{\alpha (r)+v^2}}=0, \end{aligned}$$

(73)

which may be straightforwardly solved for $f_{1,\mathrm{v}}$. Gathering these results together, in the vacuum region one thus has

$$\begin{aligned} g_{2,\mathrm{v}}= & {} v, \nonumber \\ g_{1,\mathrm{v}}= & {} \sqrt{\alpha (r)+v^2},\nonumber \\ f_{1,\mathrm{v}}= & {} \left( \sqrt{\alpha (r)+v^2} \int \frac{\partial v /\partial t}{\left( \alpha (r)+v^2 \right) ^{3/2}} \,dr \right) ^{-1}. \end{aligned}$$

(74)

Let is first consider the general case in which the fluid in the interior and exterior regions supports pressure. Suppose one specifies the form for $v(r,t_*)$ at some time $t_*$. One can then see from (73) that one also requires the profile $f_{1,\mathrm{v}}(r,t_*)$ in order to evolve v in time. Thus, both $v(r,t_*)$ and $f_{1,\mathrm{v}}(r,t_*)$ need to be specified to determine the system. One should note, however, that there is no equation determining the time evolution of $f_{1,\mathrm{v}}$; hence $f_{1,\mathrm{v}}$ is free to take any value on any time slice, provided it satisfies the boundary conditions that both $f_1$ and $\partial _r f_1$ are continuous at each boundary, as shown in Sect. 4.2. Then the time evolution of v is determined.

The situation is somewhat simpler for the case in which the fluid in the interior and exterior regions is pressureless, since one may take $f_1=1$ everywhere and at all times. Hence, if one specifies the form for $v(r,t_*)$ at some time $t_*$, one can use (73) to evolve v in time [42]. In this case, (73) becomes

$$\begin{aligned} \partial _tv+v\,\partial _rv = -\frac{M_0}{r}+\tfrac{1}{3}\varLambda r, \end{aligned}$$

(75)

which may also be derived directly by substituting the definition of M in (6) into $L_tM=0$.

In either case, with or without pressure, the exact choice of the initial profile $v(r,t_*)$ or $f_{1,\mathrm{v}}$ in the vacuum region has no physical effects on, for instance, the total redshift of a photon passing through the inhomogeneity [42], showing that the ambiguity in these functions is a gauge freedom and hence has no physical consequences.

5 Birkhoff’s theorem

One of our motivations for considering the generalised Swiss cheese model is to illustrate that Birkhoff’s theorem holds in the vacuum region, despite having time-evolving interior and exterior regions. Although its usual interpretation has recently been brought into question for physical systems of this type [44], one can demonstrate that Birkhoff’s theorem does indeed hold in the vacuum region of our generalised Swiss cheese model using a traditional wholly metric-based approach, and that it also holds directly at the level of the tetrad components by transforming into Schwarzschild–de-Sitter form [87]. In particular, we note this does not depend on the radial distribution of matter in the interior or exterior regions or its state of motion, provided spherical symmetry holds.

5.1 Comparison with previous work

The validity of Birkhoff’s theorem, or at least its usual interpretation, has recently been brought into question by [44]. To be clear, Birkhoff’s theorem states that there exist coordinates for which the metric in a vacuum region surrounding any spherically-symmetric matter distribution takes the standard Schwarzschild (de-Sitter) form with parameter $M_0$ equal to the enclosed interior mass, even when the vacuum region is itself embedded in an exterior spherically-symmetric matter distribution. Indeed, we have verified this. An immediate corollary of Birkhoff’s theorem is that, if the enclosed mass $M_0=0$, there exist coordinates for which the metric in the vacuum region takes the standard Minkowski (de-Sitter) form.

As pointed out by [44], however, a common misinterpretation of Birkhoff’s theorem is that the gravitational field anywhere inside a spherically-symmetric matter distribution is determined only by the enclosed mass. While this is true in Newtonian gravity, it does not hold in general relativity. This point is illustrated in [44] by considering the metric corresponding to a static thin spherical shell of mass $m_{\mathrm{s}}$ at coordinate radius $r=r_{\mathrm{s}}$, surrounding a spherical central object of mass $m_{\mathrm{i}}$ centered on the origin.

A further example of the gravitational field at some radius in a spherically-symmetric matter distribution being determined by material external to that radius is provided by the system analysed in [41]. As mentioned previously, this system corresponds to setting $b(t)=a(t)$ in the generalised Swiss cheese model discussed in Sect. 4, so that there is no vacuum region. In [41], this system is analysed separately using Newtonian gravity and general relativity. The former case, the Newtonian gravitational potential in the interior region is found to be independent of the properties of the exterior region, whereas the general-relativistic calculation shows that some of the tetrad components, and hence metric elements, in the interior do depend on the properties of the exterior region, such as its density $\rho _{\mathrm{e}}(t)$ and Hubble parameter $H_{\mathrm{e}}(t)$.

6 $R_{\mathrm{h}}={ct}$ cosmology

The current standard model of cosmology is based on the $\varLambda$CDM model, which provides a good fit to a wide range of cosmological observations. As pointed out by [88], however, for the best-fit $\varLambda$CDM model, the present-day Hubble distance is broadly consistent with $ct_0$ to within observational uncertainties, where $t_0$ is the current cosmic epoch. This suggests that the universe has expanded by an amount similar to what would have occurred had the expansion rate been constant. In the $\varLambda$CDM model, this correspondence is a peculiar coincidence, particularly since this situation should occur only once in the history of the universe; that we observe it to hold at the present epoch is thus intriguing.

It was therefore proposed by [45, 76, 77] that this correspondence is not coincidental, but should be satisfied at all cosmic times t. The resulting cosmological model, known as the ‘$R_{\mathrm{h}}=ct$’ model, has received considerable attention over the last few years, since it has been claimed to be favoured over the standard $\varLambda$CDM (and its variant wCDM with $w\ne -1$) by most observational data [89,90,91,92,93,94]. These claims have, however, recently been brought into question [95, 96]. In addition, the comoving Hubble radius is constant in time in the $R_{\mathrm{h}}=ct$ model, which cannot account for acoustic peak structure observed in the power spectrum of CMB anisotropies or for baryon acoustic oscillations.

In addition to observational objections, the validity of the physical argument underlying the $R_{\mathrm{h}}=ct$ model has also been criticised by a number of authors [78,79,80, 97]. Additionally, analytical claims for the model presented in [98] have also been demonstrated to be false [99].

Melia’s main proposal begins with the introduction of the ‘gravitational radius’ $R_{\mathrm{h}}(t)$, which is defined by the requirement that

$$\begin{aligned} \frac{2M(R_{\mathrm{h}}(t),t)}{R_{\mathrm{h}}(t)} \equiv 1, \end{aligned}$$

(76)

where, as previously, we adopt natural units $c=G=1$ and $M(r,t)=\frac{4}{3}\pi \rho (t)r^3$ is the mass-energy contained with a sphere of physical radius r at time t. Indeed, substituting this form for M(r, t) into (76), one immediately finds that $1/R^2_{\mathrm{h}}(t) = \frac{8}{3}\pi \rho (t)$. The key point in Melia’s argument is the assertion that, in order to satisfy Weyl’s postulate, the comoving gravitational radius $\hat{r}_{\mathrm{h}}(t)\equiv R_{\mathrm{H}}(t)/S(t)$ should be independent of t, where S(t) is the scale factor defined in Sect. 2.2. In other words, each fluid particle has a fixed value of $\hat{r}_{\mathrm{h}}$.

Then, following Melia’s assumption that $k=0=\varLambda$, the standard Friedmann equation (18) immediately allows one to make the identification $R_{\mathrm{h}}(t) = 1/H(t)$, which is the Hubble radius. Since $H(t)=\partial _t S(t)/S(t)$, the comoving gravitational (Hubble) radius in this case is given by

$$\begin{aligned} \hat{r}_{\mathrm{h}}(t) = \frac{1}{H(t)S(t)} = \frac{1}{\partial _t S(t)}. \end{aligned}$$

(77)

The requirement that $\hat{r}_{\mathrm{h}}(t)$ is constant therefore implies $S(t) \propto t$ and so $R_{\mathrm{h}}(t)= 1/H(t) = t$ or, on momentarily abandoning natural units, one obtains the eponymous $R_{\mathrm{h}}(t)=ct$. It is worth noting that substituting $H(t)=1/t$ into the dynamical cosmological field equation (19) yields Melia’s so-called ‘zero active mass’ condition $\rho +3p = 0$, which is equivalent to demanding that the overall cosmological fluid has the equation-of-state parameter $w=-\tfrac{1}{3}$ at all epochs.

The argument given in [45] for supposing that $\hat{r}_{\mathrm{H}}(t)=\text{ constant }$ is that, according to Weyl’s postulate, any proper distance in an FLRW spacetime must be the product of the scale factor S(t) and some fixed co-moving radial coordinate, and that the definition of $R_{\mathrm{h}}(t)$ as a gravitational radius in (76) implies that it must be a proper distance. No real justification is given for this latter assertion.

In the next section, we show that the requirement $\hat{r}_{\mathrm{h}}(t)=\text{ constant }$ does not follow from the definition (76). In doing so, our investigations below also elucidate the behaviour of a number of ‘horizons’ during the general-relativistic evolution of a spherically-symmetric self-gravitating matter distribution; although straightforward and interesting, this behaviour does not appear to have been widely discussed in the literature.

7 Evolution of horizons

In a homogeneous and isotropic cosmological model, let us consider an imaginary spherical boundary of radius a(t) that is comoving with the fluid and centred on some arbitrary origin. From the discussion in Sect. 4, the equation of motion for a(t) is $L_ta(t) = \dot{a} = H(t)a(t)$ (since $f_1=1$ in this case), where H(t) is the Hubble parameter characterising the evolution of the fluid. If M(t) denotes the mass-energy contained within this sphere, we define the corresponding Schwarzschild radius $R_{\mathrm{S}}(t)$ as the solution of

$$\begin{aligned} 1-\frac{2M(t)}{R_{\mathrm{S}}(t)} -\tfrac{1}{3}\varLambda R^2_{\mathrm{S}}(t) \equiv 0, \end{aligned}$$

(78)

which clearly reduces to $R_{\mathrm{S}}(t) \equiv 2M(t)$ if $\varLambda =0$. We also define the Hubble radius $R_{\mathrm{H}}(t) \equiv 1/H(t)$; note that this coincides with Melia’s gravitational radius $R_{\mathrm{h}}(t)$ in the case $k=0=\varLambda$, but differs from it in more general cosmological models (although such models were not considered by Melia).

Table 1 Evolution of the comoving radius a(t), its rate of change $\dot{a}(t)$, the mass-energy M(t) enclosed within a(t), the Schwarzschild radius (or radii) $R_{\mathrm{S}}(t)$ defined in (78) and the Hubble radius $R_{\mathrm{H}}(t)\equiv 1/H(t)$ for a selection of analytical spatially-flat $(k=0)$ expanding cosmological models, with cosmological constant $\varLambda$ and fluid equation-of-state parameter w, whose evolution is determined by the Hubble parameter H(t)

We now consider the behaviour of a(t), $R_{\mathrm{S}}(t)$ and $R_{\mathrm{H}}(t)$ for a selection of analytical spatially-flat $(k=0)$ expanding cosmological models, with cosmological constant $\varLambda$ and fluid equation-of-state parameter w, whose evolution is determined by the Hubble parameter H(t). We note that, in the spatially-flat ($k=0$) case, a(t) is the proper distance from the origin to the spherical boundary under consideration, and that $\dot{a}$ is its rate of change with respect to the proper time of an observer comoving with the fluid.⁶ The results are presented in Table 1. The values of w considered correspond to dust $(w=0)$, radiation $(w=\tfrac{1}{3})$ and Melia’s zero-active-mass condition $(w=-\tfrac{1}{3})$. It is worth noting that it is only in the case $w=0$ that the mass-energy M(t) contained within the comoving radius a(t) is constant; for other values of w the presence of non-zero pressure means that the fluid does work and hence M(t) changes with time.

Fig. 2

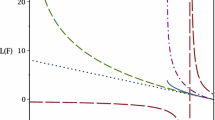
Behaviour of quantities listed in Table 1 for the case $\varLambda =0$. Top left: dust ($w=0$ with $M_0=\tfrac{9}{16}$), top right: radiation ($w=\tfrac{1}{3}$ with $M_0 = 1$), bottom: zero active mass ($w=-\tfrac{1}{3}$ with $M_0=\tfrac{1}{2}$)

For $\varLambda =0$, the behaviour of the quantities listed in the table is shown in Fig. 2. For both the dust and radiation cases, one sees that a(t), $R_{\mathrm{S}}(t)$ and $R_{\mathrm{H}}(t)$ cross at a single point that we denote by $t=t_*$, which coincides with $\dot{a}(t)$ dropping to 1 (or c in standard units). This behaviour is quite general and holds for any positive value of the parameter $M_0$ in Table 1. Thus, the comoving radius a(t) initially lies outside the Hubble radius. Indeed, one may consider that $\dot{a}$ is allowed to be greater than c during this initial period due to the ‘superhorizon’ (or, more correctly, super-Hubble-radius) nature of a(t). Note that from the Friedmann equation, we know that

$$\begin{aligned} \frac{1}{R_{\mathrm{H}}^2(t)} \equiv H^2(t) = \frac{8\pi \rho }{3} + \frac{\varLambda }{3}, \end{aligned}$$

(79)

where we consider the general case with $\varLambda \ne 0$. Multiplying the above by $a^2$ gives us

$$\begin{aligned} \dot{a}^2 = \frac{2M}{a} + \frac{\varLambda a^2}{3}. \end{aligned}$$

(80)

Hence we see that when $\dot{a}=1$, $a = R_{\mathrm{H}}$ and also $a = R_{\mathrm{S}}$. This is precisely what we see in Fig. 2. a(t) enters the Hubble radius $R_{\mathrm{H}}(t)$ at precisely the same moment as it exits the Schwarzschild radius $R_{\mathrm{S}}(t)$; it is allowed to do the latter, since the fluid at the boundary is moving at speed c at this instant. Thus, one has two ‘horizon crossings’ taking place simultaneously and in opposite directions, which is not usually pointed out in the literature. Moreover, one sees that there is no reason for the Hubble radius to be comoving, which contradicts the central assumption of the $R_{\mathrm{h}}=ct$ model. It is also worth noting that in the case of dust, for which the pressure vanishes everywhere, one can consistently ‘cut-off’ the fluid at the boundary a(t), and thereby consider a finite fluid ball surrounded by vacuum; the results for this case are precisely those given above.

In fact, we can consider the case with a finite, pressureless ball in order to verify that the physics is correct. Consider a sphere of radius a(t) filled with dust, embedded in a vacuum. Its evolution must still follow that described in Fig. 2, such that it expands with time and eventually crosses $R_{\mathrm{S}}$. Hence it is the time reversed equivalent of a collapsing ball of dust. In the latter case, the physical event horizon exists only once the boundary of the sphere crosses the point $r=2M(t)$ (for the $\varLambda =0$ case). Therefore, we can view the expanding sphere as a white hole, which has a horizon at $R_{\mathrm{S}}$, where objects are only allowed to move out initially. Once the boundary of the sphere crosses the horizon, the physical characteristics of the horizon cease to exist, such that it becomes physically possible for objects to fall in through the horizon. To verify that the crossing of the fluid boundary over $R_{\mathrm{S}}$ is possible, we can calculate the speed at which a hypothetical observer on $R_{\mathrm{S}}$ would move as measured by a comoving observer on the boundary of the sphere, as it crosses $R_{\mathrm{S}}$. One can show that the observed speed is given by $-g_2 + \frac{dR_{\mathrm{S}}(t)}{dt}$, which is valid for any $\varLambda$ and equation of state. As discussed above, when the crossing occurs, the fluid moves at speed c; hence the comoving observer sees $R_{\mathrm{S}}$ move at the speed of light when he/she crosses it, for the dust case. This is not problematic, as it is impossible to have an observer hover at $R_{\mathrm{S}}$ up until the point in time at which the ball crosses the horizon. In addition, the horizon vanishes when the edge of the fluid crosses it; hence the fluid is able to cross the horizon.

Note that when we have non-zero pressure, we can no longer ‘cut-off’ the fluid at the boundary a(t); hence we cannot consider a case where the various lines have physical characteristics.

The bottom panel in Fig. 2 shows the behaviour for the case $w=-\frac{1}{3}$, which corresponds to the zero active mass condition required by the $R_{\mathrm{h}}=ct$ model. Clearly, in this case, the radii a(t), $R_{\mathrm{S}}(t)$ and $R_{\mathrm{H}}(t)$ all depend linearly on t. If one chooses $M_0=\frac{1}{8}$, then one obtains the special case in which $a(t)=R_{\mathrm{S}}(t)=R_{\mathrm{H}}(t)$ and $\dot{a}(t)=1$ at all times. When $M_0 > \tfrac{1}{8}$, one has $\dot{a}(t)>1$ and a(t) lies inside the Schwarzschild radius and outside the Hubble radius at all times (this is illustrated in Fig. 2, for which $M_0=\tfrac{1}{2}$). Conversely, if $M_0 < \tfrac{1}{8}$, one has $\dot{a}(t)<1$ and a(t) lies outside the Schwarzschild radius and inside the Hubble radius for all t.

The behaviour of the quantities listed in Table 1 for $\varLambda \ne 0$ are illustrated in Fig. 3.

Fig. 3

Behaviour of quantities listed in Table 1 for the case $\varLambda \ne 0$. Top: dust ($w=0$), bottom: radiation ($w=\tfrac{1}{3}$); in both cases $M_0=4$ and $\varLambda =0.1$

In both cases, the values of $M_0$ and $\varLambda$ have been chosen so that, at least for some values of t, the condition $1-9M^2(t)\sqrt{\varLambda } > 0$ is satisfied and hence there exist two positive solutions for $R_{\mathrm{S}}(t)$, which correspond to the Schwarzschild radius and the de Sitter radius, respectively.

In the case of dust (top panel), the mass-energy M(t) enclosed within the spherical boundary a(t) is constant, as expected, and thus so too are the two solutions for $R_{\mathrm{S}}(t)$. One again sees that each solution for $R_{\mathrm{S}}(t)$ intersects with a(t) and $R_{\mathrm{H}}(t)$ at a single point, and that at both these intersections one has $\dot{a}(t)=1$, as we expect from equation (80). Thus, as in the case $\varLambda =0$, the comoving radius a(t) initially lies outside the Hubble radius and enters it at precisely the same moment as it exits the Schwarzschild radius, at which point the fluid at the boundary a(t) is moving at speed c. In the presence of non-zero $\varLambda$, however, the boundary a(t) later exits the Hubble radius again, at precisely the same moment that it enters the de Sitter radius, at which point the fluid at the boundary is again moving with speed c. It is again worth noting in this dust case that the absence of pressure allows one consistently to ‘cut-off’ the fluid at the boundary a(t), and thereby consider a finite fluid ball surrounded by vacuum with $\varLambda \ne 0$, and obtain identical results. In this case we again have a white hole, with a physical horizon at the Schwarzschild radius inside which objects are swept in, which ceases to exist at the moment in time the edge of the fluid crosses it.

The same generic behaviour to that outlined above is also seen for radiation in the bottom panel of Fig. 3. In this case, however, the non-zero pressure means that the fluid does work as it expands and so the mass-energy M(t) contained within a(t) decreases with time. Consequently, one initially has $1-9M^2(t)\sqrt{\varLambda } < 0$ and hence no positive solution for $R_{\mathrm{S}}(t)$. As M(t) decreases, however, one eventually has $1-9M^2(t)\sqrt{\varLambda } > 0$ and so obtains two positive solutions for $R_{\mathrm{S}}(t)$, which again correspond to the Schwarzschild and de Sitter radii, respectively.

8 Discussion and conclusions

We have presented a comparison of our tetrad-based methodology for solving the Einstein field equations for spherically-symmetric systems with the traditional Lemaître–Tolman–Bondi (LTB) model. Although the LTB model is widely used, it has a number of limitations. In particular, in its usual form it is restricted to pressureless systems. Moreover, the LTB model is typically expressed in comoving coordinates and thus provides a Lagrangian picture of the fluid evolution that can be difficult to interpret. Perhaps most importantly, however, even in the absence of vacuum regions the LTB metric contains a residual gauge freedom that necessitates the imposition of arbitrary initial conditions to determine the system evolution. As a consequence, we have for some time adopted a different, tetrad-based method for solving the Einstein field equations for spherically-symmetric systems. The method was originally presented in [39] in the language of geometric algebra, and was recently re-expressed in the more traditional tetrad notation in [40, 41]. The advantages of the tetrad-based approach are that it can straightforwardly accommodate pressure, has no gauge ambiguities (except in vacuum regions) and is expressed in terms of a ‘physical’ (non-comoving) radial coordinate. As a result, in contrast to the LTB model, the method has a clear and intuitive physical interpretation. Indeed, the gauge choices employed result in equations that are essentially Newtonian in form.

In comparing our tetrad-based methodology with the LTB model, we have focussed particularly on the issues of gauge ambiguity and the use of comoving versus ‘physical’ coordinate systems. We have also clarified the correspondences, where they exist, between the two approaches. As an illustration, we applied both methods to the classic examples of the Schwarzschild and Friedmann–Lemaître–Robertson–Walker (FLRW) spacetimes. In the former, we demonstrate that although the tetrad-based and LTB approaches both employ synchronous time coordinates and are based on trajectories of radially-infalling particles released from rest at infinity, the two methods lead to very different results corresponding to the use of Painlevé–Gullstrand and Lemaître coordinates, respectively. For the FLRW spacetime, we find that the LTB approach leads one to work directly in terms of the scale factor, whereas the tetrad-based method leads naturally to a description in terms of the Hubble parameter, which is a measurable quantity. Moreover, considerable gauge-fixing was required in the LTB model to obtain a definite solution, but this was unnecessary in the tetrad-based approach.

We have previously applied our tetrad-based method to modelling the evolution of a finite-size, compensated, spherically-symmetric object with continuous radial density and velocity profiles that is embedded in an expanding background universe, assuming zero pressure throughout [42, 43]. We have also previously used the approach to obtain solutions describing a point mass residing in an expanding universe containing a cosmological fluid with pressure [40], and later a finite spherical region of uniform interior density embedded in a background of uniform exterior density, where the pressure may be non-zero in both regions [41]. To illustrate further the use of our tetrad-based approach, we here extended the analysis in [41] to a generalised form of ‘Swiss cheese’ model, which consists of an interior spherical region surrounded by a spherical shell of vacuum that is embedded in an exterior background universe. In general, we allow the fluid in the interior and exterior regions to support pressure, and we do not demand that the interior region be compensated. We find that much of the analysis in [41], including the specification of boundary conditions, can be applied with little modification, but additional care is needed in determining the solution in the vacuum region, which requires some gauge-fixing, as might be expected.

We paid particular attention to the form of the solution in the vacuum region and verified the validity of Birkhoff’s theorem, the usual interpretation of which has recently been brought in question [44]. As pointed out in [44], Birkhoff’s theorem is often used to support the common belief that in a vacuum, the gravitational field is only affected by the interior mass. We note that that this is incorrect.

The above investigations allowed us to re-examine critically the original theoretical arguments set out in [45, 76, 77] for the so-called $R_{\mathrm{h}} = ct$ cosmological model, which has recently received considerable attention. After pointing out a number of objections to the $R_{\mathrm{h}} = ct$ based on recent observational data, we consider in particular the central assumption underlying the original theoretical argument for the model, namely that the comoving Hubble distance should be constant. We demonstrate that this is not required, and so find no reliable theoretical basis for the $R_{\mathrm{h}}= ct$ model.

These considerations in turn elucidated the behaviour of a number of ‘horizons’ during the general-relativistic evolution of homogeneous and isotropic cosmological models. In particular, we considered the evolution of an imaginary spherical boundary of radius a(t) that is comoving with the fluid and centred on some arbitrary origin. For a selection of analytical spatially-flat cosmological models, we compared a(t) to the Schwarzschild and Hubble radii. In the case of vanishing cosmological constant, we find the generic behaviour (both for dust and radiation models) that the comoving radius a(t) initially lies outside the Hubble radius, but eventually enters it at precisely the same moment as it exits the Schwarzschild radius; it is allowed to do the latter, since the fluid at the boundary is moving at speed c at this instant. Thus, one has two ‘horizon crossings’ taking place simultaneously and in opposite directions. In the case $\varLambda \ne 0$, one can obtain two positive solutions for $R_{\mathrm{S}}(t)$, which correspond to the Schwarzschild radius and the de Sitter radius, respectively. One again finds that the comoving radius a(t) initially lies outside the Hubble radius and enters it at precisely the same moment as it exits the Schwarzschild radius, at which point the fluid at the boundary a(t) is moving at speed c. In the presence of non-zero $\varLambda$, however, the boundary a(t) later exits the Hubble radius again, at precisely the same moment that it enters the de Sitter radius, at which point the fluid at the boundary is again moving with speed c. This interesting behaviour is not usually pointed out in the literature.