Skip to main content
SpringerLink
Log in

Thin-disk models in an integrable Weyl–Dirac theory

  • Research Article
  • Published:
General Relativity and Gravitation Aims and scope Submit manuscript

Abstract

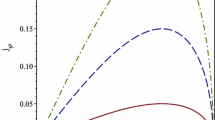
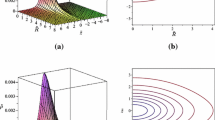
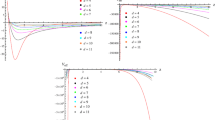
We construct a class of static, axially symmetric solutions representing razor-thin disks of matter in the Integrable Weyl–Dirac theory proposed in Israelit (Found Phys 29:1303, 1999). The main differences between these solutions and the corresponding general relativistic one are analyzed, focusing on the behavior of physical observables (rotation curves of test particles, density and pressure profiles). We consider the case in which test particles move along Weyl geodesics. The same rotation curve can be obtained from many different solutions of the Weyl–Dirac theory, although some of these solutions present strong qualitative differences with respect to the usual general relativistic model (such as the appearance of a ring-like density profile). In particular, for typical galactic parameters all rotation curves of the Weyl–Dirac model present Keplerian fall-off. As a consequence, we conclude that a more thorough analysis of the problem requires the determination of the gauge function \(\beta \) on galactic scales, as well as restrictions on the test-particle behavior under the action of the additional geometrical fields introduced by this theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Binney, J., Tremaine, S.: Galactic Dynamics, 2nd ed. Princeton University Press, Princeton (2008)

  2. Karas, V., Huré, J.-M., Semerák, O.: Gravitating discs around black holes. Class. Quantum Gravity 21, R1 (2004)

    Article  ADS  MATH  Google Scholar 

  3. Semerák, O.: Towards Gravitating Discs Around Stationary Black Holes. arXiv:gr-qc/0204025

  4. Bonnor, W.A., Sackfield, A.: The interpretation of some spheroidal metrics. Comm. Math. Phys. 8, 338 (1968)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  5. Morgan, T., Morgan, L.: The gravitational field of a disk. Phys. Rev. 183, 1097 (1969)

    Article  ADS  Google Scholar 

  6. Morgan, L., Morgan, T.: Gravitational field of shells and disks in general relativity. Phys. Rev. D 2, 2756 (1970)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  7. Bičák, J., Lynden-Bell, D., Katz, J.: Relativistic disks as sources of static vacuum spacetimes. Phys. Rev. D 47, 4334 (1993)

    Article  ADS  MathSciNet  Google Scholar 

  8. Vogt, D., Letelier, P.S.: Exact general relativistic perfect fluid disks with halos. Phys. Rev. D 68, 084010 (2003)

    Article  ADS  Google Scholar 

  9. Coimbra-Araújo, C.H., Letelier, P.S.: A thin disk in higher-dimensional space-time and dark matter interpretation. Phys. Rev. D 76, 043522 (2007)

    Article  ADS  Google Scholar 

  10. Miyamoto, M., Nagai, R.: Three-dimensional models for the distribution of mass in galaxies. Publ. Astron. Soc. Jpn. 27, 533 (1975)

    ADS  Google Scholar 

  11. González, G.A., Letelier, P.S.: Exact general relativistic thick disks. Phys. Rev. D 69, 044013 (2004)

    Article  ADS  MathSciNet  Google Scholar 

  12. Vogt, D., Letelier, P.S.: Relativistic models of galaxies. Mon. Not. R. Astron. Soc. 363, 268–284 (2005)

    Article  ADS  Google Scholar 

  13. Coimbra-Araújo, C.H., Letelier, P.S.: Gravity with extra dimensions and dark matter interpretation: phenomenological example via Miyamoto–Nagai galaxy. Braz. J. Phys. 42, 100 (2012)

    Article  ADS  Google Scholar 

  14. Begeman, K.G.: HI Rotation Curves of Spiral Galaxies. PhD. Thesis, Rijksuniversiteit Groningen (1987)

  15. Begeman, K.G.: HI rotation curves of spiral galaxies—I.NGC3198. Astron. Astrophys. 223, 47–60 (1989)

    ADS  Google Scholar 

  16. de Blok, W.J.G., McGaugh, S.S., Rubin, V.: High-resolution rotation curves of Low Surface Brightness galaxies—II. Mass models. Astrophys. J. 122, 2396–2427 (2001)

    Google Scholar 

  17. de Blok, W.J.G., McGaugh, S.S.: The dark and visible matter content of low surface brightness disc galaxies. Mon. Not. R. Astron. Soc. 290, 533 (1997)

    Article  ADS  Google Scholar 

  18. Zurita, A., Relaño, M., Beckman, J.E., Knapen, J.H.: Ionized gas kinematics and massive star formation in NGC 1530. Astron. Astrophys. 413, 73 (2004)

    Article  ADS  Google Scholar 

  19. de Blok, W.J.G.: The core-cusp problem. Adv. Astron. 2010, 789293 (2010)

  20. Navarro, J.F., Frenk, C.S., White, S.D.M.: The structure of cold dark matter halos. Astrophys. J. 462, 563 (1996)

    Article  ADS  Google Scholar 

  21. Einasto, J.: Dark Matter. arXiv:0901.0632v2 [astro-ph.CO]

  22. Sanders, R.H.: The Dark Matter Problem: A Historical Perspective. Cambridge University Press, Cambridge (2010)

    Google Scholar 

  23. Rodrigues, D.C., Letelier, P.S., Shapiro, I.L.: Galaxy rotation curves from general relativity with renormalization group corrections. JCAP 04, 020 (2010)

    Article  ADS  Google Scholar 

  24. Brownstein, J.R., Moffat, J.W.: Galaxy rotation curves without nonbaryonic dark matter. Astrophys. J. 636, 721–741 (2006)

    Article  ADS  Google Scholar 

  25. Sanders, R.H., McGaugh, S.S.: Modified Newtonian dynamics as an alternative to dark matter. Ann. Rev. Astron. Astrophys. 40, 263–317 (2002)

    Article  ADS  Google Scholar 

  26. Weyl, H.: Gravitation and electricity. In: O’Rafeartaigh (ed.) The Dawning of Gauge Theory, pp. 24–37. Princeton University Press, Princeton (1997)

  27. Dirac, P.A.M.: Long range forces and broken symmetries. Proc. R. Soc. Lond. A 333, 403–418 (1973)

    Google Scholar 

  28. Canuto, V., Adams, P.J., Hsieh, S.-H., Tsiang, E.: Scale-covariant theory of gravitation and astrophysical applications. Phys. Rev. D 16(6), 1643–1663 (1977)

    Article  ADS  MathSciNet  Google Scholar 

  29. Israelit, M.: Matter creation by geometry in an integrable Weyl–Dirac theory. Found. Phys. 29, 1303 (1999)

    Article  MathSciNet  Google Scholar 

  30. Carroll, R.: Remarks on Weyl Geometry and Quantum Mechanics. arXiv:0705.3921v3 [gr-qc]

  31. Israelit, M.: Primary matter creation in a Weyl–Dirac cosmological model. Found. Phys. 32, 295 (2002)

    Article  MathSciNet  Google Scholar 

  32. Israelit, M.: Quintessence and dark matter created by Weyl–Dirac geometry. Found. Phys. 32, 945 (2002)

    Article  MathSciNet  Google Scholar 

  33. Israelit, M.: A Weyl–Dirac cosmological model with DM and DE. Gen. Relativ. Gravit. 43, 751 (2011)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  34. Mirabotalebi, S., Jalalzadeh, S., Sadegh Movahed, M., Sepangi, H.R.: Weyl–Dirac predictions on galactic scales. Mon. Not. R. Astron. Soc. 385, 986 (2008)

    Article  ADS  Google Scholar 

  35. Letelier, P.S.: Stability of circular orbits of particles moving around black holes surrounded by axially symmetric structures. Phys. Rev. D 68, 104002 (2003)

    Article  ADS  MathSciNet  Google Scholar 

  36. Folland, G.B.: Weyl manifolds. J. Differ. Geom. 4, 145 (1970)

    MATH  MathSciNet  Google Scholar 

  37. O’Neill, B.: Semi-Riemannian Geometry with Applications to Relativity. Academic Press, New York (1983)

    MATH  Google Scholar 

  38. Buchdahl, H.A.: Reciprocal static metrics and scalar fields in the general theory of relativity. Phys. Rev. 115, 1325 (1959)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  39. Griffiths, J.B., Podolský, J.: Exact Space-Times in Einstein’s General relativity. Cambridge University Press, Cambridge (2009)

  40. Taub, A.H.: Space-times with distribution-valued curvature tensors. J. Math. Phys. 21, 1423 (1980)

    Article  ADS  MathSciNet  Google Scholar 

  41. Arfken, G.B., Weber, H.J.: Mathematical Methods for Physicists, 5th ed. Harcourt Academic Press, Burlington (2001)

  42. Jackson, J.D.: Classical Electrodynamics, 3rd ed. Wiley, New York (1999)

  43. Landau, L.D., Lifshitz, E.M.: Fluid Mechanics, Course of Theoretical Physics vol. 6, 2nd ed. Elsevier, Amsterdam (1987)

Download references

Acknowledgments

R.S.S.V. thanks Davi C. Rodrigues for helpful discussions about the astrophysics of galaxies, Mark Israelit for valuable comments on an earlier version of this manuscript and Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for financial support. This work is dedicated to the memory of Prof. Patricio S. Letelier, who passed away after the elaboration of the first draft of this manuscript.

Author information

Authors and Affiliations

  1. Instituto de Física “Gleb Wataghin”, Universidade Estadual de Campinas, Campinas, SP, 13083-859, Brazil

    Ronaldo S. S. Vieira

  2. Departamento de Matemática Aplicada-IMECC, Universidade Estadual de Campinas, Campinas, SP, 13081-970, Brazil

    Patricio S. Letelier

Authors
  1. Ronaldo S. S. Vieira
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Patricio S. Letelier
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ronaldo S. S. Vieira.

Additional information

In memoriam to Patricio S. Letelier.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Vieira, R.S.S., Letelier, P.S. Thin-disk models in an integrable Weyl–Dirac theory. Gen Relativ Gravit 46, 1641 (2014). https://doi.org/10.1007/s10714-013-1641-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10714-013-1641-7

Keywords

Search

Navigation