Skip to main content
SpringerLink
Log in

Influence of heterogeneities on crack propagation

  • Original Paper
  • Published:
International Journal of Fracture Aims and scope Submit manuscript

Abstract

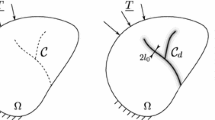
The influence of material heterogeneities is studied in the context of dynamic failure. We consider a pre-strained plate problem, the homogeneous case of which has been widely studied both experimentally and numerically. This setup is used to isolate the effects of the elastic field resulting from pre-straining and stress wave interactions throughout the crack propagation by adding stiffer and denser regions in the plate. While the crack tip is pushed away by stiffer inclusions, it is attracted to the denser ones. With the presence of denser media, only a portion of the total elastic energy in the system is effectively used to drive crack propagation, leading to a drop in the velocity of its tip in comparison to the homogeneous case. Crack branching is then observed at velocities much lower than the limiting velocity of the material, questioning the validity of crack velocity to be a criterion for crack branching. Instead, we introduce an effective stored energy to analyze the crack velocity and the emergence of crack branching instabilities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Notes

  1. The limiting velocities are in the range of 0.5–0.65 \(c_R\) for glass, 0.58–0.62 \(c_R\) for PMMA, and \(0.3{-}0.45 c_R\) for Homalite-100, see Ravi-Chandar (2004) and references therein.

References

  • Albertini G, Kammer D (2017) Supershear transition of dynamic mode II fracture in heterogeneous elastic media. J Mech Phys Solids (submitted)

  • Barenblatt G (1962) The mathematical theory of equilibrium cracks in brittle fracture. Adv Appl Mech 7(1):55–129

    Article  Google Scholar 

  • Belytschko T, Liu WK, Moran B, Elkhodary K (2014) Nonlinear finite elements for continua and structures, 2nd edn. Wiley, Hoboken

    Google Scholar 

  • Ben-Zion Y (2008) Collective behavior of earthquakes and faults: Continuum-discrete transitions, progressive evolutionary changes, and different dynamic regimes. Rev Geophys 46(4):RG4006

  • Bleyer J, Molinari JF (2017) Microbranching instability in phase-field modelling of dynamic brittle fracture. Appl Phys Lett 110(15):151903

    Article  Google Scholar 

  • Bleyer J, Roux-Langlois C, Molinari JF (2017) Dynamic crack propagation with a variational phase-field model: limiting speed, crack branching and velocity-toughening mechanisms. Int J Fract 204:79–100

  • Bobaru F, Zhang G (2015) Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. Int J Fract 196(1–2):59–98

    Article  Google Scholar 

  • Bouchbinder E, Goldman T, Fineberg J (2014) The dynamics of rapid fracture: instabilities, nonlinearities and length scales. Rep Prog Phys 77(4):046501

    Article  Google Scholar 

  • Camacho G, Ortiz M (1996) Computational modelling of impact damage in brittle materials. Int J Solids Struct 33:2899–2938

    Article  Google Scholar 

  • Chen W, Ravichandran G (1996) Static and dynamic compressive behavior of aluminum nitride under moderate confinement. J Am Ceram Soc 79(3):579–584

    Article  Google Scholar 

  • Clark A, Irwin G (1966) Crack-propagation behaviors. Exp Mech 6(6):321–330

    Article  Google Scholar 

  • Courant R, Friedrichs K, Lewy H (1967) On the partial difference equations of mathematical physics. IBM J Res Dev 11(2):215–234

    Article  Google Scholar 

  • Cox B, Gao H, Gross D, Rittel D (2005) Modern topics and challenges in dynamic fracture. J Mech Phys Solids 53(3):565–596

    Article  Google Scholar 

  • Dugdale D (1960) Yielding of steel sheets containing slits. J Mech Phys Solids 8(2):100–104

    Article  Google Scholar 

  • Fineberg J, Bouchbinder E (2015) Recent developments in dynamic fracture: some perspectives. Int J Fract 196(1–2):33–57

    Article  Google Scholar 

  • Fineberg J, Gross S, Marder M, Swinney H (1991) Instability in dynamic fracture. Phys Rev Lett 67(4):457

    Article  Google Scholar 

  • Fineberg J, Gross S, Marder M, Swinney H (1992) Instability in the propagation of fast cracks. Phys Rev B 45(10):5146

    Article  Google Scholar 

  • Fisher D, Dahmen K, Ramanathan S, Ben-Zion Y (1997) Statistics of earthquakes in simple models of heterogeneous faults. Phys Rev Lett 78(25):4885

    Article  Google Scholar 

  • Fleck N, Deshpande V, Ashby M (2010) Micro-architectured materials: past, present and future. In: Proceedings of the royal society of London a: mathematical, physical and engineering sciences, vol 466. The Royal Society, pp 2495–2516

  • Goldman T, Livne A, Fineberg J (2010) Acquisition of inertia by a moving crack. Phys Rev Lett 104(11):114301

    Article  Google Scholar 

  • Ha Y, Bobaru F (2010) Studies of dynamic crack propagation and crack branching with peridynamics. Int J Fract 162(1–2):229–244

    Article  Google Scholar 

  • Hillerborg A, Modeer M, Petersson P (1976) Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem Concr Res 6:773–782

    Article  Google Scholar 

  • Johnson J, Holloway D (1968) Microstructure of the mist zone on glass fracture surfaces. Philos Mag 17(149):899–910

    Article  Google Scholar 

  • Livne A, Bouchbinder E, Fineberg J (2008) Breakdown of linear elastic fracture mechanics near the tip of a rapid crack. Phys Rev Lett 101(26):264–301

    Article  Google Scholar 

  • Livne A, Bouchbinder E, Svetlizky I, Fineberg J (2010) The near-tip fields of fast cracks. Science 327(5971):1359–1363

    Article  Google Scholar 

  • Livne A, Cohen G, Fineberg J (2005) Universality and hysteretic dynamics in rapid fracture. Phys Rev Lett 94(22):224–301

    Article  Google Scholar 

  • Marder M (1991) New dynamical equation for cracks. Phys Rev Lett 66(19):2484

    Article  Google Scholar 

  • Marder M (1998) Adiabatic equation for cracks. Philos Mag B 78(2):203–214

    Article  Google Scholar 

  • Molinari JF, Gazonas G, Raghupathy R, Rusinek A, Zhou F (2007) The cohesive element approach to dynamic fragmentation: the question of energy convergence. Int J Numer Methods Eng 69(3):484–503

    Article  Google Scholar 

  • Murali P, Guo T, Zhang Y, Narasimhan R, Li Y, Gao H (2011) Atomic scale fluctuations govern brittle fracture and cavitation behavior in metallic glasses. Phys Rev Lett 107(21):215–501

    Article  Google Scholar 

  • Ortiz M, Pandolfi A (1999) Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis. Int J Numer Methods Eng 44:1267–1282

    Article  Google Scholar 

  • Palmer A, Rice J (1973) The growth of slip surfaces in the progressive failure of over-consolidated clay. Proc R Soc Lond A Math Phys Sci 332(1591):527–548

    Article  Google Scholar 

  • Ramulu M, Kobayashi A (1985) Mechanics of crack curving and branching—a dynamic fracture analysis. Int J Fract 27(3):187–201

    Article  Google Scholar 

  • Ravi-Chandar K (2004) Dynamic fracture. Elsevier, Amsterdam

    Google Scholar 

  • Ravi-Chandar K, Knauss W (1984) An experimental investigation into dynamic fracture: III. On steady-state crack propagation and crack branching. Int J Fract 26(2):141–154

    Article  Google Scholar 

  • Ruiz G, Ortiz M, Pandolfi A (2000) Three-dimensional finite-element simulation of the dynamic Brazilian tests on concrete cylinders. Int J Numer Methods Eng 48(7):963–994

    Article  Google Scholar 

  • Sagy A, Cohen G, Reches Z, Fineberg J (2006) Dynamic fracture of granular material under quasi-static loading. J Geophys Res Solid Earth 111(B4):B04406

  • Seelig T, Gross D (1999) On the interaction and branching of fast running cracks—a numerical investigation. J Mech Phys Solids 47(4):935–952

    Article  Google Scholar 

  • Sharon E, Fineberg J (1999) Confirming the continuum theory of dynamic brittle fracture for fast cracks. Nature 397(6717):333–335

    Article  Google Scholar 

  • Sharon E, Gross S, Fineberg J (1995) Local crack branching as a mechanism for instability in dynamic fracture. Phys Rev Lett 74(25):5096

    Article  Google Scholar 

  • Snozzi L, Caballero A, Molinari J (2011) Influence of the meso-structure in dynamic failure simulation of concrete under tensile loading. Cem Concr Res 41:1130–1142

    Article  Google Scholar 

  • Song JH, Wang H, Belytschko T (2008) A comparative study on finite element methods for dynamic fracture. Comput Mech 42(2):239–250

    Article  Google Scholar 

  • Wolff C, Richart N, Molinari JF (2015) A non-local continuum damage approach to model dynamic crack branching. Int J Numer Methods Eng 101(12):933–949

    Article  Google Scholar 

  • Xu XP, Needleman A (1994) Numerical simulations of fast crack growth in brittle solids. J Mech Phys Solids 42(9):1397–1434

    Article  Google Scholar 

  • Yoffe E (1951) The moving Griffith crack. Lond Edinb Dublin Philos Mag J Sci 42(330):739–750

    Article  Google Scholar 

  • Zhang Z, Wu F, Gao W, Tan J, Wang Z, Stoica M, Das J, Eckert J, Shen B, Inoue A (2006) Wavy cleavage fracture of bulk metallic glass. Appl Phys Lett 89(25):251917

    Article  Google Scholar 

  • Zhou F (1996) Study on the macroscopic behavior and the microscopic process of dynamic crack propagation. Ph.D. thesis, The University of Tokyo, Tokyo

  • Zhou F, Molinari JF, Shioya T (2005) A rate-dependent cohesive model for simulating dynamic crack propagation in brittle materials. Eng Fract Mech 72(9):1383–1410

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Civil Engineering Institute, Materials Science and Engineering Institute, Ecole Polytechnique Fédérale de Lausanne (EPFL), Station 18, 1015, Lausanne, Switzerland

    Okan Yılmaz & Jean-François Molinari

  2. Ecole des Ponts ParisTech, Laboratoire Navier UMR 8205 (ENPC-IFSTTAR-CNRS), Université Paris-Est, 6-8 av. Blaise Pascal, Cité Descartes, 77455, Champs-sur-Marne, France

    Jérémy Bleyer

Authors
  1. Okan Yılmaz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jérémy Bleyer
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jean-François Molinari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Okan Yılmaz.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yılmaz, O., Bleyer, J. & Molinari, JF. Influence of heterogeneities on crack propagation. Int J Fract 209, 77–90 (2018). https://doi.org/10.1007/s10704-017-0239-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10704-017-0239-6

Keywords

Search

Navigation