Skip to main content
SpringerLink
Log in

Irreversibility in the Derivation of the Boltzmann Equation

  • Published:
Foundations of Physics Aims and scope Submit manuscript

Abstract

Uffink and Valente (Found Phys 45:404–438, 2015) claim that there is no time-asymmetric ingredient that, added to the Hamiltonian equations of motion, allows to obtain the Boltzmann equation within the Lanford’s derivation. This paper is a discussion and a reply to that analysis. More specifically, I focus on two mathematical tools used in this derivation, viz. the Boltzmann–Grad (B–G) limit and the incoming configurations. Although none of them are time-asymmetric ingredients, by themselves, I claim that the use of incoming configurations, as taken within the B–G limit, is such a time-asymmetric ingredient. Accordingly, this leads to reconsider a kind of Stoßzahlansatz within Lanford’s derivation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. In Boltzmann’s derivation, Stoßzahlansatz, sometimes wrongly called the hypothesis of molecular chaos as Uffink and Valente point out, was assumed at any time. With Lanford’s derivation, there is only a factorization condition at the initial time. See Sects. 2.2 and 6 of the paper.

  2. This section is a summary based on Uffink and Valente [20] and Cercignani et al. [2, Chapter 4]. For technical details, see also Gallagher et al. [3] and Golse [5].

  3. I follow the notation used by Uffink and Valente [20] and Golse [6, p. 3]. I emphasize that, in Gallagher [3, p. 5], \(\omega _{ij}\) is instead defined as \(\frac{q_i-q_j}{a}\), from the particule i to the particule j.

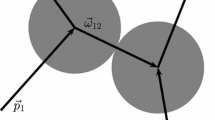
  4. Indeed, two particules 1 and 2 are about to collide if their relative distance \(\omega _{12}\) decreases with time, i.e., if \(\frac{d}{dt} |q_2 -q_1|^2\le 0\), which implies that \(\omega _{12} \cdot (p_1-p_2) \ge 0\) with our notations.

  5. The use of the B–G limit avoids thus to meet the recurrence objection since the recurrence theorem rests on the assumption that N is finite (Jones [8, p. 105] and Valente [21, p. 321]).

  6. Norton [14, p. 218] points out that extensionless points with the B–G limit are problematic with respect to determinism. When \(a\rightarrow 0\) the direction of particles after each collision is no longer deterministic. Valente [21, p. 320] reinforces this point in emphasizing that the vector \(\omega _{12}\) corresponding to the relative position of the centers of two hard spheres that are going to collide is no more defined when \(a \rightarrow 0\). In addition, Golse [6, p. 35] suggests that the appearance of irreversibility could thus be linked with such appearance of indeterminism:

    Another factor that contributes to the irreversibility is that B–G limit implies that \(r \rightarrow 0\) [i.e., \(a \rightarrow 0\)]. While \(r > 0\), laws of collisions are reversible because there is a unique vector \(n_{kl}\) [i.e., \(\omega _{12}\)] with respect to the position of particles k and l [i.e., 1 and 2]. Instead, when \(r \rightarrow 0\), the definition of the collision integral [...] requires the vector n, analogous to \(n_{kl}\), which is now randomly and uniformly distributed on the sphere.

    However, the relationship, if there is any, between the appearance of indeterminism in the laws of collision and the loss of invariance under time-reversal for the BBGKY hierarchy is still not clear.

  7. The VE describes the evolution of the probability density in phase-space that a particle is located at the position q with momentum p when the interaction between particles is given by a sum of two-body potentials of the form : \(\phi ^{(N)}(q_{1} - q_{2}) = \frac{1}{N} \phi _{0}(q_{1} - q_{2})\). The BE and the VE thus both describe the evolution of the probability density \(f_t(q,p)\) of a N-body system. The VE is : \(\frac{\partial }{\partial t}f_t(q,p)+\frac{p}{m} \cdot \frac{\partial }{\partial q}f_t(q,p)=-\mathcal {F}(q) \frac{\partial }{\partial p}f_t(q,p)\) where \(\mathcal {F}(q)\) is an integral that depends on the potential \(\phi _{0}\) and \(f_t(q,p)\) [12, p. 75]. In addition, both equations are derived from the Hamiltonian equations of motion of N particles when the number of particles tends to infinity.

  8. Unlike the BE, the VE is indeed derived from a system of N particles that do not collide: “The Vlasov equation is the kinetic model for collisionless gases or plasmas” ([4, p. 2], My emphasis). In addition, the derivations of the VE and the BE require two different notions of convergence.

  9. Saint-Raymond claims even more that the use of the incoming configurations is required to rigorously define the formal solution of the BBGKY hierarchy with integrals (private communication).

  10. This corresponds to the use of Dyson’s time-dependent perturbation theory in Uffink and Valente [20, p. 418].

  11. See also Spohn [18] on this point.

References

  1. Brown, H., Myrvold, W., Uffink, J.: Boltzmann’s H theorem, its discontents, and the birth of statistical mechanics. Stud. Hist. Philos. Modern Phys. 40, 174–191 (2009)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  2. Cercignani, C., Illner, R., Pulvirenti, M.: The Mathematical Theory of Diluted Gases. Springer, New York (1994)

    Book  MATH  Google Scholar 

  3. Gallagher, I., Saint-Raymond, L., Texier, B.: From Newton to Boltzmann : hard spheres and short-range potentials. In: Zurich Lectures in Advanced Mathematics, EMS Publications (2014). arXiv:1208.5753

  4. Golse, F.: The Mean-Field Limit for the Dynamics of Large Particle Systems . “Journées Equations aux Derivées Partielles”, Exp. No. IX, 47 pp., Univ. Nantes, Nantes (2003). http://www.cmls.polytechnique.fr/perso/golse/Surveys/FGMeanField03

  5. Golse, F.: Boltzmann–Grad limit. Scholarpedia 8(10), 9141 (2013). http://www.scholarpedia.org/article/Boltzmann-Grad_limit

  6. Golse, F.: De Newton à Boltzmann et Einstein: validation des modèles cinétiques et de diffusion. Séminaire BOURBAKI, 66, 2013–2014, 1083 (2014). http://arxiv.org/pdf/1412.0253v1

  7. Grad, H.: On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 2, 331–407 (1949)

    Article  MathSciNet  MATH  Google Scholar 

  8. Jones, N. J.: Ineliminable idealizations, phase transitions, and irreversibility. PhD thesis, The Ohio State University (2006). https://etd.ohiolink.edu/!etd.send_file?accession=osu1163026373&disposition=inline

  9. King, F.: BBGKY hierarchy for positive potentials. Ph.D. Dissertation, Dept. Mathematics, Univ. California, Berkeley (1975)

  10. Lanford, O.E.: Time evolution of large classical systems. In: Moser, J. (ed.) Dynamical Systems, Theory and Applications. Lecture Notes in Theoretical Physics, vol. 38, pp. 1–111. Springer, Berlin (1975)

    Chapter  Google Scholar 

  11. Lanford, O.E.: On the derivation of the Boltzmann equation. Asterisque 40, 117–137 (1976)

    MathSciNet  Google Scholar 

  12. Lanford, O.E.: The hard sphere gas in the Boltzmann–Grad limit. Physica 106A, 70–76 (1981)

    Article  ADS  Google Scholar 

  13. Lebowitz, J.L.: Microscopic dynamics and macroscopic laws. In: Horton, C.W. Jr., Reichl, L.E., Szebehely, V.G. (eds.) Long-Time Prediction in Dynamics, presentations from the workshop held in March 1981 in Lakeway, TX, pp. 220–233. Wiley, New York

  14. Norton, J.: Approximation and idealization: why the difference matters. Philos. Sci. 79(2), 207–232 (2012)

    Article  MathSciNet  Google Scholar 

  15. Saint-Raymond, L.: L’irréversibilité, une histoire de probabilités. In: Conference UPMC February 21 (2013). http://video.upmc.fr/differe.php?collec=CS_C_sac5&video=7

  16. Saint-Raymond, L.: Mini course—from particle systems to collisional kinetic equations—Class 2 (2015). http://strato.impa.br/videos/2015-elliptic-kinetic-partial-differential-equations/elliptic_kinetic_partial_differential_equations_20150708_laure_02.mp4

  17. Sklar, L.: Physics and Chance: Philosophical Issues in the Foundations of Statistical Mechanics. Cambridge University Press, Cambridge (1993)

    Book  Google Scholar 

  18. Spohn, H.: On the integrated form of the BBGKY hierarchy for hard spheres (2006). http://arxiv.org/pdf/math-ph/0605068

  19. Uffink, J.: Compendium of the foundations of classical statistical physics. In: Butterfield, J., Earman, J. (eds.) Handbook for the Philosophy of Physics. Elsevier, Amsterdam (2007)

    Google Scholar 

  20. Uffink, J., Valente, G.: Lanford’s theorem and the emergence of irreversibility. Found. Phys. 45, 404–438 (2015)

    Article  MathSciNet  MATH  ADS  Google Scholar 

  21. Valente, G.: The approach towards equilibrium in Lanford’s theorem. Eur. J. Philos. Sci. 4(3), 309–335 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. Villani, C.: (Ir)reversibilité et entropie. Séminaire Poincaré XV, Le Temps, Institut Henri Poincaré, Paris, pp. 17–75 (2010). http://cedricvillani.org/wp-content/uploads/2012/08/P18.Bourbaphy

Download references

Acknowledgements

Earlier versions of this article were presented at the 25th biennial meeting of the Philosophy of Science Association, the 18th UK and European Conference on Foundations of Physics, and the British Society for the Philosophy of Science 2016 annual conference. I wish to thank the participants for their helpful comments. I am also grateful to Anouk Barberousse for her insightful comments and the organization of workshops at Sciences, Normes, Decision (FRE 3593, CNRS & Université Paris-Sorbonne) that allow me to discuss this work. Thank you in particular to Sorin Bangu, Nicolas Fillion, Cyrille Imbert, Johannes Lenhard, Robert Moir, and Jos Uffink for comments and discussions. I am also most grateful to Giovanni Valente and Laure Saint-Raymond for their comments on previous drafts of this paper and their contribution to enhancing the quality of the article. This work was supported by “MOVE-IN Louvain” Incoming Post-doctoral Fellowship, co-funded by the Marie Curie Actions of the European Commission.

Author information

Authors and Affiliations

  1. Institut Supérieur de Philosophie, Université catholique de Louvain, Louvain-la-Neuve, Belgium

    Vincent Ardourel

Authors
  1. Vincent Ardourel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Vincent Ardourel.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ardourel, V. Irreversibility in the Derivation of the Boltzmann Equation. Found Phys 47, 471–489 (2017). https://doi.org/10.1007/s10701-017-0072-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10701-017-0072-9

Keywords

Search

Navigation