Bank Contingent Capital: Valuation and the Role of Market Discipline

Abstract

This paper develops a structural model to evaluate contingent capital notes (CCN) of Basel III under alternative regulatory closure rules. Our dynamic model has a fixed default barrier and at specific discrete time points an additional higher default barrier depending on the closure threshold. The closed-form expressions of CCN and subordinated debts (SD) in the simple Merton model are presented to understand the convex relationship between the price and capital ratio trigger of CCN and to examine the effects of closure rules on CCN and SD through their derivatives’ properties. Our numerical results in the more general model show that a lax closure rule increases the price of SD and distorts the risk information of issuing banks, but not so for CCN. The policy implications are that CCN are more effective than SD in terms of enhancing market discipline because the price/yield information of CCN is more sensitive to the issuing bank’s risk than SD and will not be distorted by regulatory closure rules.

Appendices

Appendix 1

When R is negative, the payoffs of the CCN, P _CCN (t), become:

$$ \begin{array}{l}{P}_{CCN}(t)=\left\{\begin{array}{l}c\kern0.5em CCN\kern6.5em if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix>kA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)- Mix\ge RA\left({t}_i\right)\&\tau >{t}_i\\ {}CCN\kern3.5em \begin{array}{ccc}\hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\left\{\begin{array}{l} if\kern0.5em A(T)-D(T)- Mix>kA(T)\&\tau >T\\ {} if\kern0.5em kA\left({t}_i\right)<A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)\ge CCN\&\tau >{t}_i\end{array}\right.\\ {}A\left(\tau \right)-D\left(\tau \right)\kern4.62em \left\{\begin{array}{l} if\kern0.5em A(T)-D(T)- Mix>kA(T)\&\tau \le T\\ {} if\kern0.5em kA\left({t}_i\right)<A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)\ge CCN\&\tau \le {t}_i\end{array}\right.\\ {}A\left({t}_i\right)-D\left({t}_i\right)\kern2em \begin{array}{cc}\hfill \hfill & \hfill \kern2em \hfill \end{array}\kern0.5em if\kern0.5em kA\left({t}_i\right)<A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)<CCN\&\tau >{t}_i\\ {}CCN-\left(q-k\right)A\left({t}_i\right)\kern2em if\kern0.5em 0<A\left({t}_i\right)-D\left({t}_i\right)- Mix<kA\left({t}_i\right)\&CCN>\left(q-k\right)A\left({t}_i\right)\&\tau >{t}_i\\ {}0\kern9.5em if\kern0.5em otherwise\end{array}\right.\\ {}\begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill {t}_t,\kern0.5em i=1,2,\dots, h,\kern0.5em {t}_h=T\hfill \end{array}\end{array} $$

(11)

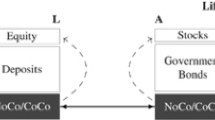
Here, CCN is the face amount of the contingent capital certificate; k is the conversion ratio of capital specified in CCN; and R is the threshold ratio implied by the regulatory closure rule under which the regulator will intervene and liquidate the bank, and it may not be the same as the minimum capital requirement q set by regulators.

When R is negative, the payoffs of the subordinated debt (SD), P _SD (t), at time t are:

$$ \begin{array}{l}{P}_{SD}(t)=\left\{\begin{array}{l}c\kern0.5em SD\kern6.5em if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix\ge RA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)>SD\&\tau >{t}_i\\ {}A(T)-D(T)\kern3.5em if\kern0.5em A(T)-D(T)- Mix\ge RA(T)\&0\le A(T)-D(T)<SD\&\tau >T\\ {}SD\kern3.5em \begin{array}{ccc}\hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\left\{\begin{array}{l} if\kern0.5em A(T)-D(T)- Mix\ge RA(T)\&A(T)-D(T)\ge SD\&\tau >T\\ {} if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)\ge SD\&\tau >{t}_i\end{array}\right.\\ {}A\left(\tau \right)-D\left(\tau \right)\kern3.5em \left\{\begin{array}{l} if\kern0.5em A(T)-D(T)- Mix\ge RA(T)\&A(T)-D(T)\ge SD\&\tau \le T\\ {} if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)\ge SD\&\tau \le {t}_i\end{array}\right.\\ {}A\left({t}_i\right)-D\left({t}_i\right)\kern2em \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\kern0.5em if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\&0\le A\left({t}_i\right)-D\left({t}_i\right)<SD\&\tau >{t}_i\\ {}0\kern8em if\kern0.5em otherwise\end{array}\right.\\ {}\begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill {t}_t,\kern0.5em i=1,2,\dots, h,\kern0.5em {t}_h=T\hfill \end{array}\end{array} $$

(12)

Here, SD is the face amount of subordinated debt, and R is the regulatory capital threshold under which regulators would close the bank.

Appendix 2

The payoffs of CCN, assuming defaults can only happen at discrete auditing times, are:

$$ \begin{array}{l}P{O}_{CCN}(t)=\left\{\begin{array}{l}c\kern0.5em CCN\kern6.5em if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix>kA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)- Mix\ge RA\left({t}_i\right)\\ {}CCN\kern3.5em \begin{array}{ccc}\hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\kern0.24em \left\{\begin{array}{l} if\kern0.5em A(T)-D(T)- Mix>kA(T)\\ {} if\kern0.5em kA\left({t}_i\right)<A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\end{array}\right.\\ {}CCN-\left(q-k\right)A\left({t}_i\right)\kern3em if\kern0.24em 0<\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix\le kA\left({t}_i\right)\&CCN>\left(q-k\right)A\left({t}_i\right)\\ {}0\kern10.5em if\kern0.5em otherwise\end{array}\right.\\ {}\begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill {t}_t,\kern0.5em i=1,2,\dots, h,\kern0.5em {t}_h=T\hfill \end{array}\end{array} $$

(B.1)

Similarly, the payoffs of SD, assuming defaults can only happen at discrete auditing times, are:

$$ \begin{array}{l}P{O}_{SD}(t)=\left\{\begin{array}{l}c\kern0.5em SD\kern6.5em if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix\ge RA\left({t}_i\right)\\ {}SD\kern3.5em \begin{array}{ccc}\hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\left\{\begin{array}{l} if\kern0.5em A(T)-D(T)- Mix\ge RA(T)\&A(T)-D(T)\ge SD\\ {} if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\&A\left({t}_i\right)-D\left({t}_i\right)\ge SD\end{array}\right.\\ {}A\left({t}_i\right)-D\left({t}_i\right)\kern2em \begin{array}{cc}\hfill \hfill & \hfill \hfill \end{array}\kern0.5em if\kern0.5em A\left({t}_i\right)-D\left({t}_i\right)- Mix<RA\left({t}_i\right)\&0\le A\left({t}_i\right)-D\left({t}_i\right)<SD\\ {}0\kern8em if\kern0.5em otherwise\end{array}\right.\\ {}\begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \begin{array}{cccc}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\hfill & \hfill {t}_t,\kern0.5em i=1,2,\dots, h,\kern0.5em {t}_h=T\hfill \end{array}\end{array} $$

(B.2)

Using the asset and deposit processes of Eqs. (4) and (5) under a risk-neutral pricing measure Q, the solutions for the first term to the third term of CCN and SD payoffs can be derived in a simple Merton-type model with a constant interest rate. For the fourth term of CCN and SD, by using the change of measure from Qto Q', the dynamics of a bank’s assets under the risk-neutralized measure Q' are:

$A\left({t}_i\right)=A\left({t}_0\right) \exp \left(\left(r-\lambda \kappa +0.5{\sigma}_A^2\right){t}_i+{\sigma}_A{W}_{A,{t}_i}^{Q\hbox{'}}+{\displaystyle \sum_{n={N}_{t_0}}^{N_{t{t}_i}} \ln {Y}_n}\right)$.

Using a similar pricing procedure, the solution to the fourth term can also be obtained.

The immediate impact of granting a higher capital ratio trigger k is best demonstrated by the following derivative property:

$$ \begin{array}{l}\frac{\partial {e}^{-r{t}_i}P{O}_{CCN}\left({t}_i\right)}{\partial k}={\displaystyle \sum_{m\ge 0}\frac{e^{-\overline{\lambda}{t}_i}{\left(\overline{\lambda}{t}_i\right)}^m}{m\kern0.5em !}}\kern0.5em \left[\frac{\partial cCCN\mathrm{N}\left( \min \left({d}_{k,{t}_i},{d}_{R,{t}_i}\right)\right)}{\partial k}+\frac{\partial CCN\left(\mathrm{N}\left({d}_{k,T}\right)+\mathrm{N}\left({d}_{k,{t}_i}\right)-\mathrm{N}\left({d}_{R,{t}_i}\right)\right)}{\partial k}\right.\\ {}\left.+\frac{\partial CCN\mathrm{N}\left( \min \left({d}_{0,{t}_i},{d}_{2,{t}_i}\right)\right)}{\partial k}-\frac{\partial \left(q-k\right)A\left({t}_0\right)\mathrm{N}\left( \min \left({d}_{0,{t}_i},{d}_{1,{t}_i}\right)\right)}{\partial k}\right]\end{array} $$

Using the chain rule, the solution of the first term in the above equation can be obtained as:

$$ \begin{array}{l}\frac{\partial \mathrm{N}\left( \min \left({d}_{k,{t}_i},{d}_{R,{t}_i}\right)\right)}{\partial k}=\frac{\partial \mathrm{N}\left( \min \left({d}_{k,{t}_i},{d}_{R,{t}_i}\right)\right)}{\partial \min \left({d}_{k,{t}_i},{d}_{R,{t}_i}\right)}\times \frac{\partial \min \left({d}_{k,{t}_i},{d}_{R,{t}_i}\right)}{\partial k}\\ {}=\frac{1}{\sqrt{2\pi }}{e}^{-0.5{d}_{k,{t}_i}^2}\frac{1}{\sigma_m\sqrt{t_i}}{1}_{\left\{{d}_{k,{t}_i}<{d}_{R,{t}_i}\right\}}\times \frac{-1}{k}=\kern0.5em {Z}_{k,{t}_i}{1}_{\left\{{d}_{k,{t}_i}<{d}_{R,{t}_i}\right\}}\frac{-1}{k}<0\end{array} $$

The other terms can also be derived by the same pricing technique.

We further investigate the effect of a regulatory closure rule with a mixture of CCN and SD. If the bond portfolio of the bank has only CCN (w ₁ = 1), then by using the chain rule we have:

$$ \begin{array}{l}\frac{\partial {e}^{-r{t}_i}P{O}_{CCN}\left({t}_i\right)}{\partial R}={\displaystyle \sum_{m\ge 0}\frac{e^{-\overline{\lambda}{t}_i}{\left(\overline{\lambda}{t}_i\right)}^m}{m\kern0.5em !}}\left[ cCCN\frac{\partial \mathrm{N}\left( \min \left({d}_{k,{t}_i},{d}_{R,{t}_i}\right)\right)}{\partial \min \left({d}_{k,{t}_i},{d}_{R,{t}_i}\right)}\times \frac{\partial \min \left({d}_{k,{t}_i},{d}_{R,{t}_i}\right)}{\partial R}+CCN\frac{\partial \mathrm{N}\left({d}_{R,{t}_i}\right)}{\partial \left({d}_{R,{t}_i}\right)}\times \frac{\partial \left({d}_{R,{t}_i}\right)}{\partial R}\right]\\ {}={\displaystyle \sum_{m\ge 0}\frac{e^{-\overline{\lambda}{t}_i}{\left(\overline{\lambda}{t}_i\right)}^m}{m\kern0.5em !}}\left[CCN\frac{1}{R}{Z}_{R,{t}_i}\left(1-c{1}_{\left\{{d}_{k,{t}_i}>{d}_{R,{t}_i}\right\}}\right)\right]\end{array} $$

Given the condition of $c{1}_{\left\{{d}_{k,{t}_i}>{d}_{R,{t}_i}\right\}}<1$, i.e., c<1 is the coupon rate, we now have:

$\frac{\partial {e}^{-r{t}_i}PO\left({t}_i\right)}{\partial R}>0,$ where ${Z}_{R,{t}_i}=\frac{1}{\sqrt{2\pi }}{e}^{-0.5{d}_{R,{t}_i}^2}\frac{1}{\sigma_m\sqrt{t_i}}$.

If the bank’s bond portfolio has equal amounts of CCN and SD (w ₁ = 0.5), then we have:

$$ \frac{\partial {e}^{-r{t}_i}PO\left({t}_i\right)}{\partial R}=0.5{\displaystyle \sum_{m\ge 0}\frac{e^{-\overline{\lambda}{t}_i}{\left(\overline{\lambda}{t}_i\right)}^m}{m!}}\left[CCN\frac{1}{R}{Z}_{R,{t}_i}\left(1-c1+{1}_{\left\{{d}_{k,{t}_i}>{d}_{R,{t}_i}\right\}}\right)+CCN\frac{1}{R}\left({Z}_{R,{t}_i}-{Z}_{R,T}\right)\right] $$

Given the condition of $c\left(1+{1}_{\left\{{d}_{k,{t}_i}>{d}_{R,{t}_i}\right\}}\right)\le 1$, i.e., c ≤ 0.5 is the coupon rate, we thus have:

$$ \frac{\partial {e}^{-r{t}_i}PO\left({t}_i\right)}{\partial R}>0. $$

Appendix 3 Simulation Method and Procedure

In this section we provide the numerical procedures that estimate the prices for SD and CCN using Eq. (9). Based on the risk-neutralized process for the assets’ value in Eq. (2), we apply Ito’s lemma to the logarithm of the value of the bank’s assets as follows:

$$ d \ln \left({A}_t\right)=\left({r}_t-\lambda \kappa -\frac{1}{2}{\sigma}_A^2\right)dt+{\sigma}_Ad{W}_{A,t}^Q+d{\displaystyle \sum_{n=0}^{N_t} \ln {Y}_n} $$

(B.3)

The risk-neutral process for the assets-to-deposits ratio, Eq. (2) minus Eq. (3), is:

$\frac{d{y}_t}{y_t}=\frac{d{A}_t}{A_t}-\frac{d{D}_t}{D_t}=\left({r}_t-\lambda \kappa -g\left({y}_t-{\overline{y}}_t\right)\right)dt+{\sigma}_Ad{W}_{A,t}^Q+d{\displaystyle \sum_{n=0}^{N_t}{Y}_n}$.

Using Ito’s lemma for the jump diffusion process, we have:

$$ d \ln \left({y}_t\right)=\left({r}_t-\lambda \kappa -g\left({y}_t-{\overline{y}}_t\right)-\frac{1}{2}{\sigma}_A^2\right)dt+{\sigma}_Ad{W}_{A,t}^Q+d{\displaystyle \sum_{n=0}^{N_t} \ln {Y}_n}. $$

In accordance with any point in time of a default event, we assume the daily time interval and time are measured in years, Δt = 1/360. Hence, the solution of (B.3), for any Δt, is:

$$ {A}_{t+\varDelta t}={A}_t \exp \left[{\displaystyle {\int}_t^{t+\varDelta t}{r}_s}ds-\left(\lambda \kappa +\frac{1}{2}{\sigma}_A^2\right)\varDelta t\right.+\sigma \left.{}_A\left({W}_{A,t+\varDelta t}^Q-{W}_{A,t}^Q\right)+{\displaystyle \sum_{n={N}_t}^{N_{t+\varDelta t}} \ln {Y}_n}\right] $$

(B.4)

The solution for the assets-to-deposits ratio, for any Δt, is:

$$ {y}_{t+\varDelta t}={y}_t \exp \left[{\displaystyle {\int}_t^{t+\varDelta t}{r}_s}ds-\left(\lambda \kappa +\frac{1}{2}{\sigma}_A^2+g\left({y}_t-\overline{y}\right)\right)\;\varDelta t\right.+\sigma \left.{}_A\left({W}_{A,t+\varDelta t}^Q-{W}_{A,t}^Q\right)+{\displaystyle \sum_{n={N}_t}^{N_{t+\varDelta t}} \ln {Y}_n}\right] $$

(B.5)

These solutions suggest a simple way of simulating asset values at any point in time. First, we simulate the risk-neutralized interest rate process from time t to time t + Δt as:

$$ {r}_{t+\varDelta t}={r}_t+{\eta}^{*}\left({\theta}^{*}-{r}_t\right)\varDelta t+\nu \sqrt{r_t}\sqrt{\varDelta t}\varepsilon $$

where ε ~ N(0, 1) is a white noise representing the Brownian motion risk of the interest rate. This allows us to compute the form of interest: ${\displaystyle {\int}_t^{t+\varDelta t}{r}_s}ds.$ Second, we simulate z ~ N(0, 1), which is a white noise representing the Brownian motion risk of the bank’s assets. Given the correlation coefficient of the bank’s assets and the interest rate ρ _A , r ,we further compute $\left({W}_{A,t+\varDelta t}^Q-{W}_{A,t}^Q\right)={\rho}_{A,r}\sqrt{\varDelta t}\varepsilon +\sqrt{1-{\rho}_{A,r}^2}\sqrt{\varDelta t}z.$. Term (N _t + Δt  − N _t ) stands for a Poisson distribution with an intensity of λΔt. For a given value of (N _t + Δt  − N _t ), we then simulate ${\displaystyle \sum_{n={N}_t}^{N_{t+\varDelta t}} \ln {Y}_n}$, where lnY _n is normal random variables with mean μ _y and variance ${\sigma}_y^2$. Combining ${\displaystyle {\int}_t^{t+\varDelta t}{r}_s}ds$, $\left({W}_{A,t+\varDelta t}^Q-{W}_{A,t}^Q\right)$, and ${\displaystyle \sum_{n={N}_t}^{N_{t+\varDelta t}} \ln {Y}_n}$ yields a simulated value for A _t + Δt as described in Eq. (B.4).