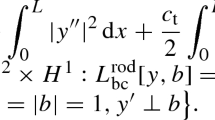Abstract
We present a novel scheme to derive nonlinearly elastic constitutive laws for special Cosserat rod modeling of nano and continuum rods. We first construct a 6-parameter (corresponding to the six strains in the theory of special Cosserat rods) family of helical rod configurations subjected to uniform strain along their arc-length. The uniformity in strain then enables us to deduce the constitutive laws by just solving the warping of the helical rod’s cross-section (smallest repeating cell for nanorods) but under certain constraints. The constraints are shown to be critical in the absence of which, the 6-parameter family reduces to a well known 2-parameter family of uniform helical equilibria. An explicit formula for the 6-parameter helical map is derived which maps atoms in the repeating cell of a nanorod to their images for the purpose of repeating cell energy minimization. A scheme for the passage from nano to continuum scale is also presented to derive the constitutive laws of a continuum rod via atomistic calculations of nanorods. The bending, twisting, stretching and shearing stiffnesses of diamond nanorods and carbon nanotubes are computed to demonstrate our theory. We show that our scheme is more general and accurate than existing schemes allowing us to deduce shearing stiffness and several coupling stiffnesses of a nanorod for the first time.









Similar content being viewed by others
References
Antman, S.S.: Nonlinear Problems of Elasticity. Springer, New York (1995)
Arroyo, M., Belytschko, T.: An atomistic-based finite deformation membrane for single layer crystalline films. J. Mech. Phys. Solids 50, 1941–1977 (2002)
Bozec, L., van der Heijden, G., Horton, M.: Collagen fibrils: nanoscale ropes. Biophys. J. 92, 70–75 (2007)
Brenner, D.W.: Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 42, 9458 (1990)
Buehler, M., Kong, Y., Gao, H.: Deformation mechanisms of very long single-wall carbon nanotubes subject to compressive loading. J. Eng. Mater. Technol. 126, 245–249 (2004)
Cai, W., Fong, W., Elsen, E., Weinberger, C.R.: Torsion and bending periodic boundary conditions for modeling the intrinsic strength of nanowires. J. Mech. Phys. Solids 56, 3242–3258 (2008)
Chandraseker, K., Mukherjee, S.: Coupling of extension and twist in single-walled carbon nanotubes. J. Appl. Mech. 73, 315–326 (2006)
Chandraseker, K., Mukherjee, S., Paci, J.T., Schatz, G.C.: An atomistic-continuum Cosserat rod model of carbon nanotubes. J. Mech. Phys. Solids 57, 932–958 (2009)
Chouaieb, N., Maddocks, J.H.: Kirchoff ’s problem of helical equilibria of uniform rods. J. Elast. 77, 221–247 (2004)
Cowper, G.R.: The shear coefficient in Timoshenko’s beam theory. J. Appl. Mech. 33, 335–340 (1966)
Ericksen, J.L.: Special topics in elastostatics. Adv. Appl. Mech. 17, 189–244 (1977)
Ericksen, J.L.: On the Cauchy-Born rule. Math. Mech. Solids 13, 199–220 (2008)
Fang, C., Kumar, A., Mukherjee, S.: Finite element analysis of carbon nanotubes based on a rod model including in-plane cross-sectional deformation. Int. J. Solids Struct. 50, 49–56 (2013)
Friesecke, G., James, R.D.: A scheme for the passage from atomic to continuum theory for thin film, nanotubes and nanorods. J. Mech. Phys. Solids 48, 1519–1540 (2000)
Gupta, P., Kumar, A.: Effect of material nonlinearity on Euler buckling of nanorods and nanotubes (2016, in preparation)
Goriely, A., Tabor, M.: Spontaneous helix hand reversal and tendril perversion in climbing plants. Phys. Rev. Lett. 80, 1564 (1998)
Gould, T., Burton, D.A.: A Cosserat rod model with microstructure. New J. Phys. 8, 137(1–17) (2006)
Goyal, S., Perkins, C., Lee, C.L.: Nonlinear dynamics and loop formation in Kirchoff rods with implications to the mechanics of DNA and cables. J. Comp. Physiol. 209, 371–389 (2005)
Hakobyan, Y., Tadmor, E.B., James, R.D.: Objective quasicontinuum approach for rod problems. Phys. Rev. B 86, 245435 (2012)
Healey, T.J.: Material symmetry and chirality in nonlinearly elastic rods. Math. Mech. Solids 7, 405–420 (2002)
Hutchinson, J.R.: Shear coefficients for Timoshenko beam theory. J. Appl. Mech. 68, 87–92 (2001)
James, R.D.: Objective structures. J. Mech. Phys. Solids 54, 2354–2390 (2006)
Klein, C.A., Cardinale, G.F.: Young’s modulus and Poisson’s ratio of CVD diamond. Diam. Relat. Mater. 2, 918–923 (1993)
Kumar, A., Healey, T.J.: A generalized computational approach to stability of static equilibria of nonlinearly elastic rods in the presence of constraints. Comput. Methods Appl. Mech. Eng. 199, 1805–1815 (2010)
Kumar, A., Mukherjee, S.: A geometrically exact rod model including in-plane cross-sectional deformation. J. Appl. Mech. 78, 011010 (2011)
Kumar, A., Mukherjee, S., Paci, J.T., Chandraseker, K., Schatz, G.C.: A rod model for three dimensional deformations of single-walled carbon nanotubes. Int. J. Solids Struct. 48, 2849–2858 (2011)
Love, A.E.H.: A Treatise on the Mathematical Theory of Elasticity. Dover, New York (2000)
Manning, R.S., Maddocks, J.H., Kahn, J.D.: A continuum rod model of sequence-dependent DNA structure. J. Chem. Phys. 105, 5626 (1996)
Miller, R., Shenoy, V.B.: Size-dependent elastic properties of nano-sized structural elements. Nanotechnology 11, 139–147 (2000)
Miller, J.T., Lazarus, A., Audoly, B., Reis, P.M.: Shapes of a suspended curly hair. Phys. Rev. Lett. 112, 068103 (2014)
Mora, M.G., Muller, S.: Derivation of the nonlinear bending-torsion theory for inextensible rods by \(\varGamma\)-convergence. Calc. Var. 18, 287–305 (2003)
Moroz, J.D., Nelson, P.: Torsional directed walks, entropic elasticity, and DNA twist stiffness. Proc. Natl. Acad. Sci. USA 94, 14418–14422 (1997)
Palanthandalam-Madpusi, H.J., Goyal, S.: Robust estimation of nonlinear constitutive law from static equilibrium data for modeling the mechanics of DNA. Automatica 47, 1175–1182 (2011)
Schmidt, B.: On the passage from atomic to continuum theory for thin films. Arch. Ration. Mech. Anal. 190, 1–55 (2008)
Simo, J.C., Vu-Quoc, L.: A geometrically-exact rod model incorporating shear and torsion-warping deformation. Int. J. Solids Struct. 27, 371–393 (1991)
Singh, R., Kumar, S., Kumar, A.: Effect of anisotropy and intrinsic twist on coupled deformations in an elastic rod (2016, in preparation)
Tadmor, E.B., Smith, G.S., Bernstein, N., Kaxiras, E.: Mixed finite element and atomistic formulation for complex crystals. Phys. Rev. B 59, 235–245 (1999)
Tersoff, J.: Empirical interatomic potential for carbon, with applications to amorphous carbon. Phys. Rev. Lett. 61, 2879–2882 (1988)
Timoshenko, S.P.: Strength of Materials, 2nd edn. Van Nostrand, Princeton (1940)
Upamanyu, M., Wang, H.L., Liang, H.Y., Mahajan, R.: Strain dependent twist stretch elasticity in chiral filaments. J. R. Soc. Interface 20, 303–310 (2008)
Wang, M.D., Yin, H., Landick, R., Gelles, J., Block, S.M.: Stretching DNA with optical tweezers. Biophys. J. 72, 1335–1346 (1997)
Yang, J.Z., Weinan, E.: Generalized Cauchy-Born rules for elastic deformations of plates, sheets and rods: Derivation of continuum models from atomistic models. Phys. Rev. B 74, 184110 (2006)
Yoshikawa, M., Mori, Y., Maegawa, M., Katagiri, G., Ishida, H., Ishitani, A.: Raman scattering from diamond particles. Appl. Phys. Lett. 62, 3114 (1993)
Acknowledgements
We thank the anonymous reviewers for their several useful suggestions. P. Gupta acknowledges support from the DST-INSPIRE fellowship.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Computing Inter-Atomic Energy of the Fundamental Domain (\(E_{FD}\)) and Its Derivatives
The energy of the fundamental domain depends on positions of the atoms within the FD as well as their images which lie within the cut-off radius. The locations of the image atoms are calculated using formula (27). Once we know these atomic locations, we can use a standard procedure to compute the inter-atomic energy of the fundamental domain. In order to minimize \(E_{FD}\) (see (30)) and also to deduce the constitutive laws (see (32) and (33)), we need to calculate the derivatives of \(E_{FD}\) with respect to atomic positions (\(\mathbf {x}_{j}\)) as well as strains which essentially implies computing the derivatives of atomic positions and their images (both \(\mathbf {x}_{j}\) and \(\mathbf{x}_{i,j}\)) with respect to \(\mathbf{x}_{j}\) and strains. The map (27) does not turn out to be useful for this purpose. In fact, the derivative of the map (27) with respect to the strain “\(\underline{\mathrm{k}}\)” (evaluated at zero strain) possesses a non-removable singularity. We, therefore, use the following formula equivalent to (27) for this purpose:
From (45), we note that computing the derivatives of \(\mathbf{x}_{i,j}\) with respect to \(\mathbf{x}_{j}\) and \(\underline{\mathrm{v}}\) are straightforward. However, computing the derivatives with respect to \(\underline{\mathrm{k}}\) necessitates taking derivatives of the rotation matrix (as well as its integral) with respect to \(\underline{\mathrm{k}}\). Analytical formulas for these derivatives are now presented for the readers’ convenience.
Appendix B: Derivative of Atomic Positions with Respect to Strains
From (45), the derivatives of \(\mathbf {x}_{i,j}\) with respect to strains follow as:
Now, we show the derivatives of the rotation matrix as well as its integral with respect to \(\underline{\mathrm{k}}\). Let \(\psi= \vert\underline{\mathrm{k}}\vert\), \(\underline{\mathrm{u}}=\frac{\underline{\mathrm{k}}}{\psi}\) denote the axis of rotation and \(\theta= s\psi\) be the angle of rotation. Also, let \([\underline{\mathrm{u}} ] _{\times}\) and \([\mathbf {e}_{i} ]_{\times}\) denote the skew symmetric matrices whose axial vectors are \(\underline{\mathrm{u}}\) and \(\mathbf {e}_{i}\) respectively. Note that the definition of \(\theta\) here is different from the earlier definition but simplify our notations below. Using Rodrigues’ formula for rotation, we get
Now, \(\underline{\mathrm{u}}\) being a constant, Rodrigues’ formula (47) can be integrated analytically which is shown below in (48). The formulas for the derivatives of (47) and (48) are also shown below. Since these formulas contain a removable singularity at \(\theta= 0\), a Taylor expanded version (with singularity removed) is used in such situations.
Similarly, the second derivative of the rotation matrix and its integral can be obtained.
Appendix C: Derivative of \([ \{\hat{\mathbf{x}}_{j} \},\hat{\boldsymbol{\lambda}}, \hat{\boldsymbol{\delta}}]\) with Respect to Strains
In this section, we first derive an expression for the derivative of \([ \{\hat{\mathbf{x}}_{j} \},\hat{ \boldsymbol{\lambda}}, \hat{\boldsymbol{\delta}}]\) with respect to strains and finally show that the second term in Eq. (32)(a) vanishes, i.e.,
We first observe that (30) holds at all strains. Differentiating the three equations in (30) with respect to strains, we then obtain
Let us define a stiffness matrix \(\mathbf{K}^{3m\times3m}\) and the linearized constraint matrix \(\mathbf{C}^{3m\times6}\) such that its block-components are as shown below:
Here \(\mathbf{I}\) is an identity matrix whereas
is a matrix formed by three components of the position vector of \(i\)th atom. We can then write (52) in the following matrix form:
Equation (54) can be inverted to obtain the derivatives of \([ \{\hat{\mathbf{x}}_{j} \},\hat{ \boldsymbol{\lambda}},\hat{\boldsymbol{\delta}}]\) with respect to strains. Now, upon block multiplication in (54), we see that \(\mathbf{C}^{T} \bigl\{\frac{\partial\hat{\mathbf {x}}_{i}}{\partial [\underline{\mathrm{v}},\underline{\mathrm{k}}]} \bigr\} = \mathbf{0}\). This further implies that \(\bigl \{\frac{\partial\hat{\mathbf {x}}_{i}}{\partial [\underline{\mathrm{v}},\underline{\mathrm{k}}]} \bigr\}\) is perpendicular to columns of \(\mathbf{C}\). Using Q-R factorization of \(\mathbf{C}\), we then obtain
Upon pre-multiplying the first set of block equations in (54) by \(\mathbf{Q2}^{T}\) and substituting (55), we then obtain
Now using (30) and (53), we get:
Finally,
Rights and permissions
About this article
Cite this article
Kumar, A., Kumar, S. & Gupta, P. A Helical Cauchy-Born Rule for Special Cosserat Rod Modeling of Nano and Continuum Rods. J Elast 124, 81–106 (2016). https://doi.org/10.1007/s10659-015-9562-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-015-9562-1
Keywords
- Cauchy-Born rule
- Special Cosserat rod
- Elastic constitutive modeling
- Helical symmetry
- Molecular mechanics