1 Introduction

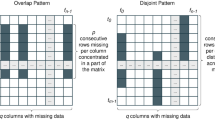
Multivariate time series data are widely prevalent in real-life domains, including medical logs (Bertsimas et al. 2021; Ahmed and Schmidt-Thieme 2023), meteorological records (Luo et al. 2018), and traffic data (Che et al. 2018). In complex systems like sensor networks, sensor breakage and data corruption are typical issues. These issues can disrupt the data collection process. Consequently, missing values can present significant challenges in multivariate time series analysis (Cini et al. 2022). Missing readings at random is known as “General Missing,” while the loss of readings at sequential timestamps or all sensors at once results in a phenomenon termed “Block Missing” (see Fig. 1). Traditionally, there are three common approaches employed to address missing values in time series data. The first approach involves simply discarding data samples that contain missing values (Acock 2005; Enders 2011). However, this method of data deletion may result in the loss of valuable information that could be derived from incomplete data (Yarkın Yıldız et al. 2022). The second approach entails utilizing machine learning models that are capable of handling time series data even when certain data points are missing (Chai et al. 2020; Tang et al. 2020). However, the mentioned approach requires using complex architectures specifically designed to handle missing values in time series. The third approach, known as imputation, involves substituting missing data with appropriate values based on observed value patterns (Amiri and Jensen 2016; Cleveland and Loader 1996; García-Laencina et al. 2010). This approach allows for the retention of as much information as possible based on observed patterns in the data.

Existing imputation approaches include neighbor-based methods (Amiri and Jensen 2016; Batista et al. 2002; Song et al. 2015; Sun et al. 2020), constraint-based methods (Song and Chen 2011; Song et al. 2013, 2011, 2013), regression-based methods (Cleveland and Loader 1996; Box et al. 2015; Peter Zhang 2003; Zhang et al. 2017), matrix factorization based methods (Luo et al. 2014; Mei et al. 2017; Yu et al. 2016) and expectation-maximization based methods (García-Laencina et al. 2010; Ghahramani and Jordan 1993; Nelwamondo et al. 2007). Recent breakthroughs in deep learning have allowed new ways to deal with missing data, including algorithms based on recurrent networks (Cao et al. 2018) and generative adversarial networks (Yoon et al. 2018). These approaches, however, presume the underlying distribution or disregard relationship information between sensors.

Graphs are a form of data structure that depicts the relationships between objects in a collection. Graph Neural Networks (GNNs) have recently gained popularity because of their high expressive capacity, permutation-invariance, local connectivity, and compositionality (Wu et al. 2020; Xu et al. 2018; Ahmed et al. 2022). GNNs can leverage the graph structure where a node’s representation vector is produced by recursively aggregating node information and altering the representation vectors of its neighbors. Multivariate time series imputation can be intuitively seen from a graph perspective (Wu et al. 2020). Sensors from multivariate time series can be considered nodes in a graph, and they are interlinked through their hidden dependency relationships. When compared to approaches that do not use structural information, GNNs have made considerable gains in data imputation (You et al. 2020), particularly in time series imputation (Kuppannagari et al. 2021; Cini et al. 2022). Despite the progress made in prior research studies that leverage GNNs for time series imputation, the learning of spatial relationships or interactions among different sensors, commonly referred to as “relational information", remains largely unexplored. More specifically, existing literature often neglects the incorporation of relational information from two important perspectives:

Unknown graph structure. While it is acknowledged that GNNs have the ability to effectively capture relational information among sensors as per existing literature (Cini et al. 2022), they exhibit certain limitations when utilized for time series imputation tasks. Current GNN-based approaches for time series imputation, rely heavily on a pre-defined graph based on simplistic measures such as similarity or attention scores between sensors to determine sensor relationships or interactions (Kuppannagari et al. 2021; Cini et al. 2022), which can be considered superficial and elementary. In the context of time series analysis, the spatial relationships among sensors cannot be assumed or provided as prior knowledge. Instead, these relationships need to be discovered and learned from the inherent dynamics present in the time series data itself. Consequently, an alternative and more effective approach would be to learn the relational information from the available data itself, as this approach enables the model to capture the underlying relationships and dependencies among sensors, which can be more adaptable to the specific patterns in the time series data.

The “over-smoothing” issue in GNNs. The phenomenon known as "over-smoothing" in GNNs has been observed, wherein repeated message passing or aggregation operations during GNN propagation can lead to excessively smoothed node representations. This effect is due to the propagation of information across graph edges through multiple GNN layers, resulting in reduced diversity and loss of nuanced features in node representations. The result is a reduced discriminative power and hindered ability of the GNNs to capture complex patterns or distinguish between different nodes in the graph, especially in the context of time series data. To address this issue, a novel approach is proposed that decouples the learning process and leverages the strengths of different neural network architectures. Specifically, GNNs are utilized for learning spatial sensor relationships, while Convolutional Neural Network-Bidirectional Long Short-Term Memory (CNN-BilLSTM) is employed to capture temporal and local patterns in the data. This specialized learning process allows for improved performance in imputation tasks.

To address these two limitations, we propose a novel model, Structure-aware Decoupled imputation network (SaD). SaD model is designed to include a graph structure learning module to capture the relationships between sensors. This module comprises a graph attention encoder to capture relationships between different sensors as it allows the model to capture the underlying relationships and dependencies between sensors instead of relying on simple similarity or attention scores between sensors. To address the second limitation, SaD decouples the learning process and leverages the strengths of different neural network architectures. Specifically, GNNs are utilized for learning spatial relationships, while CNN-BilLSTM is employed to capture temporal and local patterns in the data. This specialized learning process allows for improved performance in imputation tasks. In addition, we introduce a two-step knowledge integration process in SaD, which considers the mutual influence between different learned representations. Specifically, we propose to 1) integrate prior knowledge using an adversarial matching method and 2) integrate two categories of information (i.e., characteristics and inter-sensor interactions) by employing a shared decoder. The contributions of this work can be summarized as follows.

Fig. 1
figure 1

Diagram of time series imputation problem

Full size image

  • We propose the first decoupled time-series imputation model that incorporates sensor characteristics and relationship information.

  • In our proposed model, SaD, we present an innovative two-step knowledge integration strategy. We propose to 1) integrate prior knowledge using an adversarial matching method and 2) integrate two categories of information (i.e., characteristics and inter-sensor interactions) by employing a shared decoder.

  • Extensive experiments on real-world datasets prove the superiority of the proposed model compared to all baseline models under different settings, with an error reduction of around 15% over the former best model.

2 Related work

Time series imputation. Missing value imputation in time series has a considerable body of literature. Other than deletion-based methods (McKnight et al. 2007; Wothke 2000), and traditional interpolation methods based on statistical attributes, such as mean imputation, median imputation, and most frequent value imputation (Acuna and Rodriguez 2004; Rogier et al. 2006; Kantardzic 2011), popular approaches attempt to fill in missing values by using traditional forecasting algorithms and time series similarities. These approaches, despite their simplicity, are still commonly used today due to their effectiveness and reliability. Examples of these techniques include neighbor-based methods (Amiri and Jensen 2016; Batista et al. 2002; Song et al. 2015; Sun et al. 2020), constraint-based methods (Song and Chen 2011; Song et al. 2013, 2011, 2013), regression-based methods (Cleveland and Loader 1996; Box et al. 2015; Peter Zhang 2003; Zhang et al. 2017) such as ARIMA (Box et al. 2015), ARFIMA (Bhardwaj and Swanson 2006), and SARIMA (Hamzaçebi 2008), matrix factorization based methods (Luo et al. 2014; Mei et al. 2017; Yu et al. 2016) and expectation-maximization based methods (García-Laencina et al. 2010; Ghahramani and Jordan 1993; Nelwamondo et al. 2007).

Recently, several deep-learning algorithms have been proposed for time-series imputation (Lipton et al. 2016; Che et al. 2018; Cao et al. 2018; Tashiro et al. 2021; Cini et al. 2022). Deep learning approaches mostly employ Recurrent Neural Networks (RNNs), which are capable of capturing temporal information  (Lipton et al. 2016; Che et al. 2018; Cao et al. 2018). Earlier studies attempted to impute missing values with RNNs by concatenating timestamps with input time series data (Choi et al. 2016). Not only are RNNs used to impute time series, but also some models incorporate Gated Recurrent Units (GRUs) to extract long-term information such as the GRU-D model (Che et al. 2018). For instance, the GRU-D model (Che et al. 2018) includes a decay mechanism designed for the input variables where the hidden states are used to model missing patterns in RNNs for time series classification problems. On the other hand, BRITS (Cao et al. 2018) is entirely based on an RNN architecture and presents multivariate time series imputation with bidirectional mechanisms to account for losses in both directions. They recommend employing time delays to manage irregular time series, which is comparable to the GRU-D concept of the decay rate. Similarly, NAOMI (Liu et al. 2019) is a non-autoregressive model that takes both past and future values into account, along with adversarial training to improve the model. Nevertheless, NAOMI neglects temporal gaps since the time series data is fed into the RNN model without incorporating timestamps. Attention-based models have garnered significant attention in the realm of time series imputation. One example is the SAITS model proposed by Du et al. (2023) (Wenjie et al. 2023). The SAITS model incorporates a diagonally-masked self-attention mechanism, enabling it to effectively capture temporal dependencies and correlations between different features within the time series data.

Generative Adversarial Networks (GANs) have advanced time-series imputation (Goodfellow et al. 2014). GANs are neural networks designed for generating synthetic instances of data using two neural networks, a generator and a discriminator, that work simultaneously against each other (Goodfellow et al. 2014). The generator learns to generate false data to deceive the discriminator into identifying its samples as genuine. In contrast, the discriminator seeks to differentiate between genuine data and generated data. The generator can eventually provide reliable data. Accordingly, GANs were proposed to impute time series data, together with RNNs, to increase imputation accuracy (Luo et al. 2019). For instance, GRUI-GAN is basically a GAN model where both the generator and discriminator are based on the GRU-I cell which is a recurrent unit that follows the structure of GRU-D to get the data imputed (Luo et al. 2018). \(E^2 GAN\) is yet another model that employs an encoder-decoder RNN-based structure as the generator, addressing the complexity of training the model as well as its accuracy (Luo et al. 2019). Other successful works in the literature are entirely GAN architectures only. For example, GAIN (Yoon et al. 2018) is a generalization of GANs (Goodfellow et al. 2014) for missing data imputation. Similarly, semi-supervised GAN is a method similar to GAIN that makes full use of the label information in time series data by conditioning time series imputation on observed components and data labels at the same time (Miao et al. 2021).

Concurrently with our work, Cini et al. (2022) (Cini et al. 2022) presents GRIN, the first graph-based architecture for multivariate time series imputation, which intends to rebuild missing data in multiple channels of a multivariate time series by learning spatio-temporal representations via message passing. Another piece of work by Kuppannagari et al. (2021) (Kuppannagari et al. 2021) developed a spatial-temporal GNN-based denoising autoencoder that imputes missing data. However, it should be noted that this approach is specifically designed for data imputation tasks rather than handling time series data directly.

Graph neural networks. GNNs represent graph dependence via message passing between nodes. They encapsulate a node’s high-level representation by conveying data from its neighbors (Zhou et al. 2020). GNNs are widely employed to handle a variety of time series problems, including time series forecasting with a particular emphasis on traffic prediction (Li et al. 2017; Wu et al. 2019, 2020), anomaly detection (Zhao et al. 2020; Deng and Hooi 2021) and time-series imputation (Cini et al. 2022). Li et al. (2017), for instance, introduced a comparable design that substitutes spectral GNNs with a diffusion-convolutional network that captures spatio-temporal relationships using RNN encoder-decoder architecture. Similarly, (Wu et al. 2019) propose a novel architecture named Graph WaveNet for spatial-temporal graph modeling that alternates convolutions on temporal and spatial dimensions to capture the hidden spatial dependency in the data and handle very long sequences. Other scholars have considered using GNNs in the context of attention-based models (Vaswani et al. 2017). Chen et al. (2020), for example, employed multi-range attention to collect information in many ranges and merged it with graph convolutional RNNs to depict temporal dependence for traffic forecasting. Similarly, (Zheng et al. 2020) presented an encoder-decoder architecture with multiple spatio-temporal attention blocks for traffic prediction. Another especially intriguing field of study is focused on the detection of time series anomalies (Zhao et al. 2020; Deng and Hooi 2021). For example, Deng and Hooi (2021) present GDN (Deng and Hooi 2021), an attention-based GNN approach for anomaly identification in multivariate time series data that seeks to discover and explain deviations.

Recently, the research focus evolved to how to adapt GNNs for imputing missing values. For instance, (Spinelli et al. 2020) proposed an adversarial approach to train a GNN autoencoder for the data reconstruction task, while (You et al. 2020) introduced a bipartite graph representation for feature imputation where the feature imputation task is formulated as an edge-level prediction task. Kuppannagari et al. (2021) proposed a spatio-temporal GNN autoencoder specifically designed for data imputation. However, it is important to note that while these methods have demonstrated success in imputing missing values, they were not explicitly designed for the imputation of missing values within the context of time series data. Lately, GNNs have also been used for the imputation of multivariate time series data. Cini et al. (2022) presented GRIN (Cini et al. 2022), the first GNN architecture that aims to reconstruct missing data in distinct channels of a multivariate time series by learning spatio-temporal representations through the use of message passing. Even though the GRIN model outperforms approaches without a graph structure, this model relies on a pre-defined graph structure based on simple similarity or attention scores between sensors. In addition, they tend to over-smooth node differences, degrading reconstruction performance. In contrast, SaD addresses these issues by decoupling the learning process and leveraging the strengths of different neural network architectures. Specifically, GNNs are utilized for learning sensor spatial relationships, while CNN-BilLSTM is employed to capture temporal and local patterns. This decoupled and specialized learning process results in enhanced performance for imputation, as it effectively leverages the advantages of both spatial relationship modeling and temporal pattern modeling.

3 Problem formulation

In this paper, we focus on the task of multivariate time series imputation. In the datasets we consider for evaluation, the time series originate from the measurements of a collection of distributed sensors (i.e. measurement stations). Each of the \(\textbf{N}\) sensors measure \(\textbf{D}\) different variables, such that at time step t we have observation values \(\mathbf {\mathcal {X}_t} \in \mathbb {R}^{N \times D}\) where \(\mathbf {x_{t,i,j}}\) is the measurement of the j-th variable at the i-th sensor. We assume \(\mathbf {\mathcal {M}_{t} \in \mathbb {R}^{N \times D}}\) is a mask matrix whose values are either 0 or 1 at each time step t, where 0 indicates a missing value and 1 indicates a non-missing value. For training, we selected a subset of observations via a binary mask \(\mathbf {\mathcal {M}_{t}}\) and split the data into observations and target values via,

$$\begin{aligned}{} & {} \mathbf {x^{}_{t,i,j}} = \left\{ \begin{array}{ll} x_{t, i, j} ^{\text {obs}} &{} \text{ if } {\mathcal {M}_{t,i,j}} = 1;\\ \\ x_{t, i, j} ^{\text {target}} &{} \text{ if } {\mathcal {M}_{t,i,j}} = 0.\end{array} \right. \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \mathcal {X}_t = \mathcal {M}_{t} \odot \mathcal {X}_{t}^{\text {obs}} + (1-\mathcal {M}_{t}) \odot \mathcal {X}_{t}^{\text {target}} \end{aligned}$$
(2)

where \(\odot\) denotes the element-wise multiplication. Here, our objective is to impute the missing values using the temporal patterns and relational information included in the time series data.

Fig. 2
figure 2

Overall architecture of the SaD model

Full size image

4 Methodology

As illustrated in Fig. 2, SaD consists of a graph structure learning module, a sensor imputation module, and a two-step knowledge integration module. The graph structure learning module uses a spatio-temporal message passing mechanism to learn hidden connections among sensors. A sensor imputation module is used to extract temporal patterns and local patterns. Both the graph structure learning module and the sensor imputation module are based on the architecture of an adversarial auto-encoder (Spinelli et al. 2020). Figure 2 gives a demonstration of how the sensor imputation module and graph structure learning module collaborate with each other through a two-step knowledge integration module. We elaborate on the core components of our model below.

4.1 Graph structure learning

This module’s main objective is to capture the associations between the sensors. In order to learn the latent network structure with sensors acting as nodes and connections between them acting as edges, as shown in Fig. 2, we could utilize a GNN on the fully-connected graph inspired by the Neural Relational Inference (NRI) model (Kipf et al. 2018). This model employs graph neural networks that utilize message-passing techniques to jointly learn the relationships and dynamics based on observed data. In our case, the observed data consists of the sensor readings, and as we do not have prior knowledge about the relationships between the sensors, we learn the edge embeddings from the node embeddings through message-passing techniques. A sensor-to-sensor edge implies that the first sensor is used to mimic the behavior of the second sensor. This module comprises an encoder \(\mathbf {E_A}\) that defines high-level message passing mechanism from node-to-edge and edge-to-node message passing to capture relationships between different sensors.

Encoder \(\mathbf {E_A}\) is comprised of Graph Attention Network (GAT) that enables the model to focus on specific interactions with neighbors while processing messages. GAT (Veličković et al. 2018; Salehi and Davulcu 2020) is a neural network design that uses masked self-attentional layers. Formally, let’s represent the presence of an edge from node (i.e. sensor) \({n_i}\) to node \({n_j}\) as \({e_{ij}}\). By considering sensor features as initial node representations (i.e., \({g_i^{(0)}}\) = \(d_i\), \(\forall i \in \{1, 2, \ldots , N\}\)), the node-to-edge \(({n\rightarrow e})\) and edge-to-node \(({e\rightarrow n})\) message passing operations can be defined as follows,

$$\begin{aligned}{} & {} \, \; {n\rightarrow e}: \,\, e_{ij}= \sigma (v_s^{(l)} \, \sigma (W^{(l)} \, g^{(l-1)}_i) \,\nonumber \\{} & {} \quad \, \, \, \; \; \;+ \;v_r^{(l)} \, \sigma (W^l \, g^{(l-1)}_j )) \end{aligned}$$
(3)

Here, \({W^{(l)}} \in \mathbb {R}^{d^{(l)} \times d^{(l-1)}}\), \({v_s^{(l)}} \in \mathbb {R}^{d^{(l)}}\) and \({v_r^{(l)}} \in R^{d^{(l)}}\) represents the trainable parameters of the \({{l^{th}}}\) encoder layer where d stands for the node representation dimension in the \({l^{th}}\) encoder layer and \(\sigma\) indicates the sigmoid activation function. To normalize the relevance coefficients \(\alpha _{ij}\) of the node i’s neighbors such that they are consistent, we use the softmax function as follows:

$$\begin{aligned} \alpha _{ij}^{(l)}= \frac{\text {exp} (e_{ij}^{(l)})}{\sum _{w\varepsilon \mathcal {N}_i}{\, (e_{iw}^{(l)})}} \end{aligned}$$
(4)

where \(\mathcal {N}_i\) denotes the neighborhood of node i (i.e., the set of nodes linked to node i including node i itself).

$$\begin{aligned} {e\rightarrow n}: \,\,{g}_{i}^{(l)}= \sigma (\sum _{j\varepsilon \mathcal {N}_{i}}{\alpha _{ij}^{(l)} \, W^{(l)} \, {g}_j^{(l-1)}}) \,\, \end{aligned}$$
(5)

Accordingly, we take the output of the \(L_{th}\) encoder layer as the final node representations. Next, we will design our sensor imputation network using this learned sensor representation that encapsulates the spatial relationships and dynamics between sensors.

4.2 Sensor imputation network

This module comprises an encoder-decoder structure, as illustrated in Fig. 2, in which the encoder \(\mathbf {E_X}\) extracts local temporal features and patterns and the decoder restores the input sequence. To extract relevant temporal features, the encoder employs 2D convolutional and bidirectional LSTM layers where a 2D convolution layer is employed for extracting patterns and non-linear dependencies that exist over time, while the BiLSTM layer captures the temporal dependencies within the encoded features (Asadi and Regan 2019; Kamyab et al. 2021). Here, the decoder \(\mathbf {D_X}\) is shared with the graph structure encoder \(\mathbf {E_A}\) and sensor attributes encoder \(\mathbf {E_X}\) individually, so that composes structure-to-attribute encoder-decoder \((\mathbf {E_A \rightarrow D_X})\) and attribute-to-attribute encoder-decoder \((\mathbf {E_X\rightarrow D_X})\). For the decoder \(\mathbf {D_X}\), bidirectional LSTM layers and fully connected layers are employed.

Specifically, a 2D convolutional layer contains a kernel that slides across time series data \(\mathcal {X} \in \mathbb {R}^{N \times T \times d}\), where N stands for the number of sensors and d is the dimension of the features. A kernel of size \((N, \mathcal {W})\) that slides over the time axis where \(\mathcal {W} \le T\) and stride size is (N, 1). As a result, different kernels with varying \(\mathcal {W}\) values are applied to the input data, with the output of each kernel i being \(k_i \in R^{1 \times T \times f }\), where f denotes the filter size. All outputs are finally concatenated and expressed as \(h \in \mathbb {R}^{1 \times T \times F}\), where F is the total size of all filters.

The BiLSTM layer takes the output of the convolutional layer \(h\) and computes the forward and backward hidden states. Then, the final output of the BiLSTM layer is obtained by concatenating the forward and backward hidden states. When we join the forward and backward representation, we get the output of BiLSTM layer which represents the produced latent representation \(\mathbf {z_x}\) of the encoder \(\mathbf {E_X}\). To this end, we use a shared decoder that generates the same output from the embedding of different encoders \(\mathbf {E_A}\) and \(\mathbf {E_X}\). Accordingly, either \(\mathbf {z_x}\) or \(\mathbf {z_a}\) serves as an input to the decoder \(\mathbf {D_X}\) that generates reconstructed sensors. Here, the decoder, in a similar fashion, is made up of bidirectional LSTM and a fully connected layer with a linear activation function. This means that if data is missing, the reconstruction of input automatically fills it in based on the relational and temporal information by minimizing the loss function of both encoder-decoder architectures, \((\mathbf {E_A \rightarrow D_X})\) and \((\mathbf {E_X\rightarrow D_X})\), at all time steps. In Sect. 4.3, we go into further detail on the functionality of the structure-attribute encoder-decoder in integrating relational data.

4.3 Two-step knowledge integration

We propose a carefully designed two-step knowledge integration process. The overview of our model is illustrated in Fig. 2, where the backbone of our proposed method is two sub-nets sharing a decoder, which capture information between two views of time series.

However, separated sub-nets are unable to capture the influence between the two types of representation. Therefore, to further incorporate such information, we propose to simultaneously allow the joint distribution modeling of structure and attributes with a two-step knowledge integration paradigm, which contains:

  • Structure-attribute integration, considering the influence between two views of input time series (i.e. structure and attributes) on representing multivariate time-series, and

  • Prior knowledge integration, considering the prior distribution matching between sensors representation and sensor-to-sensor relations via an adversarial distribution matching strategy.

Structure-attribute Integration. Let \(x_i\) and \(a_i\) represent the attribute information and learned relational information, respectively, of input sequence i. Using the multi-view assumption (Chen et al. 2020; Abdi et al. 2018; Liu et al. 2017), we assume that every pair \((x_i, a_i)\) selected from the joint distribution of the two domains has a shared latent representation \(z \in \mathbb {R}^d\). Consequently, the latent codes \(\mathbf {z_x}\) and \(\mathbf {z_a}\) may be converted to (or retrieved from) any of these domains using the appropriate encoding (or decoding) algorithms, as seen in Fig. 2. A latent representation is beneficial because it helps us to translate data from one domain to another, creating a common knowledge of the data in both domains.

To address this, we let the shared decoder \(\mathbf {D_X}\) generate the same output from the paired attribute and structure embedding. Moreover, this allows the embeddings to learn inherent information between two input views. Accordingly, the designed objective corresponding to the decoder \(\mathbf {D_X}\) insures that a decoded output should be accurately reconstructed regardless of whether the input embedding is \(\mathbf {z_x}\) or \(\mathbf {z_a}\). This objective is optimized by the following loss \(L_{\text {map}}\):

$$\begin{aligned}{} & {} \min \limits _{ \theta _{x}, \theta _{a}, \phi _{x}, \phi _{a} } L_{\text {map}}=- E_{x \sim p_{X}} [E_{q_{\phi _{x}}(z_x \mid x)} [\text {log} \; p_{ \theta _{x}} (x\mid z_x) ]]\nonumber \\{} & {} \quad \; \; \; \; \; \; \; \; \; \; \; \; \; \; - \lambda \; E_{a \sim p_{X}} [E_{q_{\phi _{a}}(z_a \mid x)} [\text {log} \; p_{\theta _{a}} (x \mid z_a)]] \end{aligned}$$
(6)

where \(p_X\) represents the whole data distribution and \(q_{\phi _{x}}(z_x \mid x)\) indicates the encoder \(\mathbf {E_X}\) that encodes x to \(\mathbf {z_x}\). Similarly, \(q_{\phi _{a}}(z_a \mid x)\) indicates the encoder \(\mathbf {E_A}\) that encodes x to \(\mathbf {z_a}\). \(p_{ \theta _{x}} (x \mid z_x)\) and \(p_{\theta _{a}} (x \mid z_a)\) indicate our shared decoder that decodes \(\mathbf {z_x}\) and \(\mathbf {z_a}\) to the same output x respectively.

The first term in Eq. 6 guarantees that samples from the latent variable of the sensors attributes are in close proximity to their respective latent codes. The second term provide a connection between the latent space of the attributes and the latent space of the structure. The latent space of the sensors relational information is assumed to be a reference variable to the sensor attributes. Here, \(\lambda\) is used to tweak the relative importance of relational information.

Prior Knowledge Integration . Since we are dealing with high dimensional time-series, it becomes more difficult to impute missing data solely based on the input sequences. Therefore, it is desirable to incorporate possible prior knowledge. Accordingly, our proposed method employs the adversarial distribution matching that can impose an arbitrary prior distribution for the both latent codes which mimics the adversarial auto-encoder design in Spinelli et al. (2020); Chen et al. (2020). Accordingly, for both auto-encoders, the output of the encoder is matched with Gaussian distribution N(0, 1) considered as auxiliary distribution. The adversarial losses are summarized as follows for the two adversarial components:

$$\begin{aligned}{} & {} \min \limits _{\psi } \max \limits _{\phi _{x}} L_{\text {adv}_{-X}}= - E_{z_{p} \sim p_{(z)}} [\text {log} \; \mathcal {D} (\mathcal {N}(0,1))]\nonumber \\{} & {} \quad \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; - E_{z_{x} \sim q_{\phi _{x}}(z_x \mid x)} [\text {log} \;(1- \mathcal {D}(z_x)] \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \min \limits _{\psi } \max \limits _{\phi _{a}} L_{\text {adv}_{-A}} = - E_{z_{p} \sim p_{(z)}} [\text {log} \; \mathcal {D}(\mathcal {N}(0,1))] \nonumber \\{} & {} \quad \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; -E_{z_{a} \sim q_{\phi _{a}}(z_a \mid a)} [\text {log} \;(1- \mathcal {D}(z_a)] \end{aligned}$$
(8)

Accordingly, the final loss function can be summarized as follows:

$$\begin{aligned} \min \limits _{\psi } \max \limits _{\phi _{x}, \phi _{a}} L_\text {adv} = L_{\text {adv}_{-X}} + L_{\text {adv}_{-A}} \end{aligned}$$
(9)

where \({\psi }\) indicates the parameters of the shared discriminator \(\mathcal {D}\) which encourages both \(\mathbf {z_x}\) and \(\mathbf {z_a}\) to match the whole prior distribution p(z). Meanwhile, the proposed loss encourages the latent embeddings to match both the prior and the entire true data distribution.

4.4 Objective function

The total training loss is equal to the sum of structure-attribute integration loss and prior knowledge integration loss. In summary, the objective function of SaD is as follows:

$$\begin{aligned} \min \limits _{\Theta }\max \limits _{\Phi } L = L_{\text {map}}+ L_{\text {adv}}, \end{aligned}$$
(10)

where \(\Theta = \{\theta _x, \theta _a, \phi _x, \phi _a, \psi \}\) and \(\Phi = \{\phi _x,\phi _a\}\). Accordingly, SaD allows useful knowledge to be extracted through this additional source of guidance to closely align the structure and attribute latent spaces and thus facilitates the imputation task.

5 Experiments

In this section, we present our experiments on three real-world datasets to assess the proposed imputation model, SaD. The experimental outcomes are thoroughly examined and compared.

5.1 Datasets and baselines

We assess the utility of SaD using three real-world datasets, comprising two traffic datasets and one meteorological dataset. These datasets are listed below.

  • Beijing Air Quality Data. We assess our proposed model using the Beijing air quality dataset, which is comprised of PM2.5 observations from 36 monitoring sites with a missing rate of 13.2%. Measurements are gathered every hour from 2014/05/01 to 2015/04/30 (Yi et al. 2016; Zheng et al. 2015), which has 8,759 timestamps respectively.

  • METR-LA. A traffic dataset is made up of data collected from sensing devices on Los Angeles County highways (Li et al. 2017). For the experiment, we pick 207 sensors and gather data for 4 months, from March 1 to June 30, 2012 (Li et al. 2017; Cini et al. 2022).

  • PEMS-BAY. This traffic data is gathered by the California Transportation Agencies’ Performance Measurement System. It is characterized by a network of 325 traffic sensors in the Bay Area with six months of traffic measurements from January 1, 2017 to May 31, 2017 at five-minute intervals (Li et al. 2017; Cini et al. 2022).

We compare SaD with these baseline methods:

  • Mean imputation (MI): This method simply replacing the missing values with corresponding global mean.

  • K-nearest neighbors (KNN). This method utilize the k-nearest neighbor algorithm to impute the missing values using the weighted average based on the normalized Euclidean distance.

  • Multivariate imputation by chained equations (MICE) (White et al. 2011). The method estimates plausible values for the missing data based on the observed non-missing values by employing multiple regression and appropriately combining results obtained from each of them.

  • Matrix Factorization (MF) (Luo et al. 2014). This approach decomposes the data matrix into two low-rank matrices and fills in missing values by completing the matrices, assuming that a subset of observable values is sufficient to infer missing values.

  • ST-MVL (Yi et al. 2016). This method considers the geographical and temporal correlations. It further combines mixes several empirical models to include the benefits of global views and local views from geographical and temporal perspectives when imputing missing values.

  • GAIN (Yoon et al. 2018). This approach generalizes the Generative Adversarial Networks for data imputation, where the generator’s objective is to impute missing data and the discriminator’s objective is to differentiate between observed and imputed values.

  • GRU-D (Che et al. 2018). This method adopt Gated Recurrent Unit (GRU) along with two different trainable decay mechanisms to generate missing values.

  • BRITS (Cao et al. 2018). A model for the imputation of missing data that uses a bidirectional RNN to impute missing values in both the forward and backward directions.

  • GRIN (Cini et al. 2022). This method generalizes GNNs for multivariate time series imputation through a message passing imputation layer.

5.2 Experimental setup

Here, we created missing values during partitioning in order to get training and test sets in which these missing values were initially filled with zeros. The imputation error is consequently calculated only on missing data during the testing phase. Following previous research (Yi et al. 2016; Cini et al. 2022), we examine two cases concerning missing data: general missing and block missing. The missing scenarios are shown in Fig. 1. In the general missing scenario, missing points are distributed at random. In contrast, the block-missing scenario is usually caused by virtual server failures. In alignment with the approach employed in ST-MVL (Yi et al. 2016) and GRIN (Cini et al. 2022), we designate the months of March, June, September, and December as the test set for the Air Quality dataset. As for the METR-LA and PEMS-BAY datasets, we followed the methodology outlined in GRIN (Cini et al. 2022), wherein the data was divided into three folds, with 70% utilized for training and the remaining 10% and 20% allocated for validation and testing, respectively. In random missing, the missing data is dispersed randomly throughout the dataset. In contrast, block missing typically occurs due to failures of virtual servers. To simulate these scenarios, the GRIN (Cini et al. 2022) approach is utilized. In the case of a block missing, 5% of the available data for each sensor is randomly removed, and a failure with a 0.15% probability is simulated. The failure duration is sampled uniformly in the range of 1 to 3 h in the METR-LA and PEMS-PAY datasets and 1 to 6 h in the Air Quality dataset. For evaluation, Mean Absolute Error (MAE) and Mean Relative Error (MRE) are used as evaluation metrics (Yi et al. 2016). We maintained a consistent batch size of 128 throughout the model training process. Hyperparameter \(\lambda\) was fine-tuned to achieve optimal performance. Additionally, an early stopping strategy was incorporated if no reduction in MAE was detected after 20 epochs. A hyperparameter search is conducted for all models. The Adam optimizer  (Kingma and Ba 2015) is employed to train all models.Footnote 1

Table 1 The performance summary of MAE and MRE (%) scores for time-series imputation on different datasets
Full size table

5.3 Performance comparison for time series imputation

The goal of this experiment is to see whether SaD can improve imputation performance in a variety of circumstances when compared to the current state-of-the-art. The experiment goes as follows. On various datasets, we compared the proposed model to baseline models with a 30% missing rate. We also examine the efficiency of imputation in various missing rate scenarios on the Air Quality dataset, as shown in Tables 1 and 2. Results are reported as MAE and MRE on the test set. The findings in Tables 1 and 2 demonstrate that time-series imputation using SaD can drastically boost the accuracy of imputed values compared to other imputation models. This proves the significance of incorporating the impact between sensor properties and inter-sensor relationships into the time-series imputation problem. For instance, there is around 21% MAE reduction and 14% MRE reduction compared to the previous best model results, GRIN, in the air quality dataset. Generally, it can be concluded that in all cases, the SaD model yields improvements of around 15-23 %, in MAE and 14-22 %, in MRE over the state-of-the-art baseline models in the three datasets.

Table 2 The performance summary of MAE score in various missing rates on air quality dataset
Full size table

5.4 Performance on downstream tasks

To further analyze the imputed data, we explore how well SaD preserves the diversity and patterns of original data on downstream tasks. Since there is no ground truth data for missing values, evaluating the inaccuracy of the imputations is challenging. Therefore, we use the performance of a downstream application to assess the proposed method indirectly. Cini et al. (2022) proposed a downstream task as a proxy for assessing the quality of imputed data to circumvent this issue. They decided to mimic the existence of a sensor with no data and then let the model reconstruct the time series. Consequently, we masked the observed values of the two air quality sensors, 1014 and 1031, during model training following (Cini et al. 2022). In this experiment, our objective is to compare the reconstruction capability of the SaD mode with top-performing baseline models, namely BRITS (Cao et al. 2018) and GRIN (Cini et al. 2022). As illustrated in Fig. 3, the SaD model could closely reconstruct unseen real-world time series and mimic their diverse patterns. In this setting, the SaD model yields MAE scores of 10.39 and 13.56 for sensors 1014 and 1031, achieving improvements of around 20 %, manifested by a reduction in MAE compared to the previous best model findings, GRIN.

Fig. 3
figure 3

a Reconstruction of sensor 1014 observations. b Reconstruction of sensor 1031 observations. Both sensors were excluded from the training set

Full size image

5.5 Analysis of model components

We conducted an in-depth investigation of model components in SaD to provide a more insightful understanding of the model. The possible sources of gain are the use of a decoupled GNN architecture, the use of prior knowledge integration through adversarial loss (\(L_{\text {adv}}\)), and the use of structure-attribute integration through the auxiliary term that represents relational information learning in \(L_{\text {map}}\). Table 3 demonstrates that the performance of SaD is enhanced by the inclusion of all three components. Specifically, the whole SaD model is 15% better than the model without relational information (\(\text {SaD}_{\text {w/o structure}}\)). In addition, the performance is marginally enhanced by 2% thanks to the incorporation of prior knowledge(\(\text {SaD}_{\text {w/o prior}}\)).

Table 3 Analysis of SaD model components
Full size table

6 Conclusion

In this paper, we introduce SaD, a novel decoupled time series imputation network that can learn sensor properties and their relational information as a separate representation while still maintaining mutual influence across different sub-networks. The experimental findings on three real-world datasets show that the SaD model enhances the accuracy of time-series imputation, provides an efficient method to impute time-series data under a variety of conditions, and reconstructs unseen sensors by mimicking their distinctive patterns.