Subjectively interesting connecting trees and forests

Abstract

Consider a large graph or network, and a user-provided set of query vertices between which the user wishes to explore relations. For example, a researcher may want to connect research papers in a citation network, an analyst may wish to connect organized crime suspects in a communication network, or an internet user may want to organize their bookmarks given their location in the world wide web. A natural way to do this is to connect the vertices in the form of a tree structure that is present in the graph. However, in sufficiently dense graphs, most such trees will be large or somehow trivial (e.g. involving high degree vertices) and thus not insightful. Extending previous research, we define and investigate the new problem of mining subjectively interesting trees connecting a set of query vertices in a graph, i.e., trees that are highly surprising to the specific user at hand. Using information theoretic principles, we formalize the notion of interestingness of such trees mathematically, taking in account certain prior beliefs the user has specified about the graph. A remaining problem is efficiently fitting a prior belief model. We show how this can be done for a large class of prior beliefs. Given a specified prior belief model, we then propose heuristic algorithms to find the best trees efficiently. An empirical validation of our methods on a large real graphs evaluates the different heuristics and validates the interestingness of the given trees.

1 Introduction

Increasingly often, data presents itself in the form of a graph, be it edge- or vertex-annotated or not, weighted or unweighted, directed or undirected. Gaining insights in such graph-structured data has therefore become a topic of intense research. Much related research focuses on the discovery of local structures in the graph, with dense subgraphs or communities (Fortunato 2010) as the most prominent example.

The question this paper is focused on is: “How is a given set of vertices (the ‘query vertices’) related to each other in a given graph?” This question is distinctive from most prior work in two ways. First, the type of information it provides the user with is of a different kind than the density of a subgraph, or other kinds of local patterns. Second, the question relates to a particular set of query-vertices, i.e., it is driven by a user query. The particular approach presented in this paper adds a third important distinctive aspect (and in this way it also distinguishes itself from Akoglu et al. (2013), which is most directly related to our work—see Sect. 9): the fact that it aims to ensure that the answer to this question is subjectively interesting to the user, i.e., taking into account the prior beliefs the user holds about the graph.

Fig. 1

Trees connecting the three most recent KDD best paper award winners listed at the official ACM SIGKDD webpage (http://www.kdd.org/awards/sigkdd-best-research-paper-awards) that are also present in the Aminer ACM-Citation-network v8 (https://aminer.org/citation, Tang et al. (2008)). This is the result of our algorithm with heuristic s-IR, for three different types of prior beliefs. a A prior belief on the overall graph density. Each citation is equally interesting, and the algorithm simply prefers the smallest possible connecting tree. Note that the root of the tree is a highly cited paper. b A prior belief on the number of citations of each paper. If a user knows certain papers are widely cited, those papers are less interesting to find in the connecting tree: the user already expects this connection to exist and hence does not learn much. In this case, we find a tree with a less frequently cited paper as a root. c A combined prior belief on both the number of citations and the time difference (in publication year) between cited papers. Larger time differences between citing papers are more uncommon, and hence more interesting. The algorithm now prefers less cited and older papers. See Sect. 5.1 for more details. In all cases, the resulting trees are in direct contrast with the expectations the user has on the network

More specifically, given a graph and a set of query vertices, this paper presents a method that can explain to a user how these query vertices are connected in the graph, and this in a minimal but highly informative manner. Informative indicates that the connections should be interesting to the specific user at hand. An example: suppose we have a scientific paper citation network, where edges denote that one paper references another. Given a set of query papers, a directed tree containing these query papers is one possible way to represent interesting citation relationships between these papers. The root of the tree could represent a paper that was (perhaps indirectly) highly influential to all the papers in the query set. Figure 1 shows the results of our algorithm when we queried three recent KDD best paper award winners, when considering three different types of users (all with different prior knowledge about the network).

We consider the case of connecting the query vertices through a subgraph that has a tree structure. The main question here is: what makes a certain tree interesting to a given user? Finding connecting subgraphs between a set of vertices in a graph is a relatively novel problem, and thus the number of attempts to quantify the interestingness of such patterns is limited (see Sect. 9). One common aspect of all these approaches is that their proposed measures are objective, i.e., independent of the user at hand.

In our work, we make no attempt at proposing another objective interestingness measure. We believe that the goal of Exploratory Data Mining (EDM) is to increase a user’s understanding of his or her data in an efficient way. However, we have to consider that every user is different. It is in this regard that the notion of subjective interestingness was formalised (Silberschatz and Tuzhilin 1996) and more recently the creation of the data mining framework FORSIED that we build upon (De Bie 2011a, 2013).

This framework specifies in general terms how to model prior beliefs the user has about the data. Given a background distribution representing these prior beliefs, we may find patterns that are highly surprising to the particular user. Hence in our setting, a tree will generally be more interesting if it contains, according to the user’s beliefs, more unexpected relationships between the vertices.

Contributions To summarize, this paper contributes the following:

• We define the new problem of finding subjectively interesting trees and forests connecting a set of query vertices in a graph (Sect. 2).

• Using group theoretic methods, we provide an algorithm for efficiently modelling a highly generic class of prior beliefs, namely about the density of any particular sub-graphs. We experimentally show the efficiency by fitting a background model on a number of graphs (Sects. 4 and 6).

• We discuss two new realistic prior beliefs in more detail. We show how to formalize knowledge about time relations in a graph (Sect. 5.1). Secondly, we discuss how to model knowledge about a graph’s degree assortativity (Sect. 5.2).

• We propose heuristics for mining the most interesting trees efficiently, both for undirected and directed graphs (Sect. 7).

• We evaluate and compare the effectiveness of these heuristics on real data and study the utility of the resulting trees, showing that the results are truly and usefully dependent on the assumed prior beliefs of the user (Sect. 8).

Relation to conference version This paper is based on the conference paper (Adriaens et al. 2017). The following material is completely new:

• The pattern syntax is broader, covering also trees in undirected graphs. Previously, only connecting arborescences were discussed (directed trees). We achieved this by providing methods for finding connecting trees, forests, and branchings. This broadens applicability to both undirected and directed graphs, as well as allowing for a possible partitioning of the query vertices (Sect. 2.2).

• Thorough analysis of the Description Length of connecting trees (Sect. 3).

• A general method for efficiently fitting background distributions for a large class of prior belief types. Adriaens et al. (2017) discussed how to model prior beliefs about vertex degrees and a time-order relation between the vertices in the graph. The current paper extends this to prior knowledge on the density of any part of the adjacency matrix—a generalization of previous work, which also has important applicability in contexts beyond this work (Sects. 4.3 and 6).

• A more thorough experimental evaluation and an empirical comparison with related work. The efficiency of our proposed methods is tested in more detail on a wider variety of different types of graphs, and a direct comparison with an existing related method is added (Sect. 8).

2 Subjectively interesting trees in graphs

This section deals with the formalization of connecting trees as data mining patterns, and the introduction of a subjective interestingness measure to evaluate them. In Sect. 2.1 we introduce some notation and terminology, mostly adopted from graph theory. Section 2.2 discusses the different types of patterns used in this work, while in Sect. 2.3 we introduce the interestingness measure.

2.1 Notation and terminology

We will mostly adapt a similar notation as in Korte and Vygen (2007). A graph¹ is denoted as $G=(V,E)$, where V is the set of vertices and E is the edge set. For undirected graphs, E is a set of unordered pairs of distinct vertices. For directed graphs, E is a set of ordered pairs of distinct vertices. This definition disallows self-loops, and each pair of vertices induces at most one edge. Often we will use V(G) and E(G) to denote the vertex and edge set associated with G. For brevity, to denote that a graph F is a subgraph of G (i.e., $V(F)\subseteq V(G)$ and $E(F)\subseteq E(G)$), we may write $F\subseteq G$. We denote the adjacency matrix of a graph as A, where $\mathbf A _{ij}=1$ if and only if there is an edge connecting vertex i to j. We assume that the set of vertices V is fixed and known, and the user is interested the network’s connectivity, i.e., the edge set E, especially in relation to a set of so-called query vertices$Q\subseteq V$.

A forest is an undirected graph with no cycles. A tree is a connected forest. A tree spans a graph G if all vertices in G are part of the tree. A directed graph is a branching if the underlying undirected graph is a forest and each vertex has at most one incoming edge. An arborescence is a branching with the property that the underlying undirected graph is connected. Each arborescence has exactly one root vertex , and a unique path from this root to all other vertices.² For trees and forests, a leaf is a vertex with degree at most 1. For arborescences and branchings, a leaf is a vertex with no outgoing edge. In both cases, vertices that are not leaves are called internal vertices.

We denote both the directed and the undirected complete graph on n labeled vertices $v_1,\ldots ,v_n$ as $K_n$. The exact meaning of $K_n$ will be clear from the context.

2.2 Connecting trees, forests, arborescences and branchings as data mining patterns

The data mining task we consider is query-driven: the user provides a set of query vertices $Q\subseteq V$ between which connections may exist in the graph that might be of interest to them. In response to this query, the methods proposed in this paper will thus provide the user with a tree-structured subgraph connecting the query vertices. Trees are concise and intuitively understandable descriptions of how a given set of query vertices is related. More general classes of subgraphs would lead to a larger descriptive complexity, and are at risk of overburdening the user. Cliques and dense subgraphs are insightful and concise too, but well-studied elsewhere (see, e.g., Goldberg 1984; Lee et al. 2010; van Leeuwen et al. 2016). The methods proposed in Sect. 7 will search for interesting tree-structured subgraphs T— present in the graph G—-with the property that the leaves of T are a subset of Q. Furthermore, we may allow this tree-structured subgraph to be disconnected. In many cases, a tree connecting vertices in Q will be too large or simply not exist. One solution for this is to partition Q and find a connecting tree in each partition, leading to a different kind of pattern, i.e., a connecting forest.

To summarize, in this paper we will discuss four types of patterns (see Fig. 2). If G is undirected, we will look for connecting trees and forests. If G is directed, we will look for connecting arborescences and branchings.³$^{,}$⁴

Fig. 2

Examples of the different types of connecting subgraphs considered in this paper, all connecting the query set $Q=\{q_1,q_2,q_3,q_4\}$; a a connecting treeb a connecting forestc a connecting arborescenced a connecting branching. In all cases we have the requirement that the leaves of these connecting subgraphs are a subset of Q

2.3 A subjective interestingness measure

To model the user’s belief state about the data, the FORSIED framework proposes to use a background distribution, which is a probability distribution P over the data space (in our setting, the set of all possible edge sets E over the given set of vertices V). This background distribution should be such that probability of any particular value of the data (i.e., of any particular edge set E) under the background distribution represents the degree of belief the user attaches to that particular value. To achieve this, it was argued that a good choice for the background distribution is the maximum entropy distribution subject to the prior beliefs as constraints (De Bie 2011a, 2013).

The FORSIED framework then prefers patterns that achieve a trade-off between how much information the pattern conveys to the user (considering their belief state), versus the effort required of the user to assimilate the pattern. Specifically, De Bie (2011a) argued that the Subjective Interestingness (SI) of a pattern can be quantified as the ratio of the Information Content (IC) and the Description Length (DL) of a pattern, i.e.,

$$\begin{aligned} {\text {SI(pattern)}=\frac{\text {IC(pattern)}}{\text {DL(pattern)}},} \end{aligned}$$

where the IC is defined as the negative log probability of the pattern w.r.t. the background distribution P (see Sect. 4 for a detailed discussion). The less likely a user thinks that a certain data mining pattern is present in the data, the more information this pattern conveys to the user if the pattern were to be found in the actual data. The DL is quantified as the length of the code needed to communicate the pattern to the user (see Sect. 3 for a detailed discussion).

The methods presented in this paper aim to solve the following (directed graph) problems:

Problem 1

Given a directed graph $G = (V,E)$ and set of query vertices $Q \subseteq V$. Find a root $r\in V$ and an arborescence $A\subseteq G$ rooted at r with $\text {leaves}(A) \subseteq Q \subseteq V(A)$ that has maximal subjective interestingness.

Problem 2

Given a directed graph $G = (V,E)$ and set of query vertices $Q \subseteq V$. Find a branching $B\subseteq G$ with that has maximal subjective interestingness.

As well as the undirected variants:

Problem 3

Given an undirected graph $G = (V,E)$ and set of query vertices $Q \subseteq V$. Find a tree $T\subseteq G$ with $\text {leaves}(T) \subseteq Q \subseteq V(T)$ that has maximal subjective interestingness.

Problem 4

Given an undirected graph $G = (V,E)$ and set of query vertices $Q \subseteq V$. Find a forest $F\subseteq G$ with $\text {leaves}(F) \subseteq Q \subseteq V(F)$ that has maximal subjective interestingness.

In all cases, we can additionally constrain the depth (i.e., the diameter) of the connecting subgraphs not to be larger than a user-defined parameter k.

Since the SI depends on the background distribution and thus on the user’s prior beliefs, the optimal solution to Problems 1–4 does as well. Section 4 discusses how to efficiently infer the background distribution for a large class of prior beliefs, and how to compute the IC of a pattern. The next section discusses how the DL of trees, forests, arborescences and branchings is defined.

3 The description length of connecting trees, forests, branchings and arborescences

The goal is to find an efficient encoding for communicating a tree T to the user, with the constraint that $\text {leaves}(T) \subseteq Q \subseteq V(T)$. This constraint can be equivalently formulated by requiring all $v \in V(T) {\setminus } Q$ to be internal vertices. Communicating T can be done by first communicating the set $V(T) {\setminus } Q$ (the user already knows Q). Because $V(T) {\setminus } Q \subseteq V {\setminus } Q$, and $V {\setminus } Q$ has $2^{V{\setminus } Q}$ subsets, we need $|V{\setminus } Q|=|V|-|Q|$ bits to describe $V(T) {\setminus } Q$. Without extra knowledge on the possible connections amongst the vertices in V(T), E(T) can then be described most efficiently by enumerating over all possible trees. The following theorem enumerates all trees with the constraint that all leaf vertices are query vertices.

Theorem 1

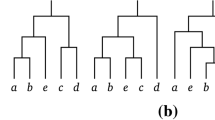
Given a set of k labeled vertices in $K_n$. There are

$$\begin{aligned} T(n,k) = \displaystyle \sum _{i=0}^k (-1)^i {{k}\atopwithdelims (){i}}(n-i)^{n-2} \end{aligned}$$

spanning trees in $K_n$, s.t. these k vertices are all internal vertices.

Fig. 3

An illustration of $T(4,1)=7$. There are 7 possible trees spanning $\{v_1,v_2,v_3,v_4\}$ such that $v_1$ is an internal vertex

Note that we do not impose any restrictions on the other $n-k$ vertices, they can be internal or leaf vertices. Figure 3 illustrates all the spanning trees for the case T(4, 1). The case $k=0$ reduces to the well-known Cayley’s formula for counting labeled trees (Cayley 1889; Moon 1970). The cases $k \in \{n-1, n\}$ reduce to $T(n,k)=0$, since any tree of size $n>1$ must have at least 2 leaves. For the case $k=n-2\ge 0$ we have $T(n,n-2)=(n-2)!$, since the only possible trees are chains (i.e., all vertices have degree $\le 2$) and there are $(n-2)!$ ways to permute the internal vertices in a chain. This latter identity is also algebraically proven in Anglani and Barile (2007, Proposition 3). We present a short proof of Theorem 1, using the inclusion-exclusion principle.

Proof

Let $S=\{\text {spanning trees in } K_n\}$. By Cayley’s formula, $|S|=n^{n-2}$. Let $\{v_1,\ldots ,v_k$} be the vertices that we require to be internal. $\forall i \in \{1,\ldots ,k\}$ define the sets $A_i=\{\text {spanning trees in } K_n \text { s.t. } v_i \text { is internal}\}$. By the inclusion-exclusion principle,

$$\begin{aligned} T(n,k) = \left| \cap A_i \right| = \left| \overline{\cup \overline{A_i}} \right|&= |S| - \left| \cup \overline{A_i} \right| \\&= n^{n-2} - \displaystyle \sum _{i=1}^k (-1)^{i-1}{{k}\atopwithdelims (){i}}\left| \overline{A_1}\cap \ldots \cap \overline{A_i} \right| . \end{aligned}$$

We can now easily compute $\left| \overline{A_1}\cap \ldots \cap \overline{A_i} \right|$. There are $(n-i)^i$ ways to add i labeled leaves to a tree consisting of $n-i$ labeled vertices (each leaf can be attached to $n-i$ possible vertices). By Cayley’s formula, the number of trees on $n-i$ labeled vertices is equal to $(n-i)^{n-i-2}$. Hence $\left| \overline{A_1}\cap \ldots \cap \overline{A_i} \right| = (n-i)^i(n-i)^{n-i-2} = (n-i)^{n-2}$, and the claim follows. $\square$

Thus, we can communicate a tree T consisting of n labeled vertices—with the requirement that a given $n-|Q|$ of the vertices have to be internal—by using

$$\begin{aligned} \text {DL}(T) = |V|-|Q|+\log (T(n,n-|Q|)) \end{aligned}$$

bits. In a very similar manner, we can count the number of spanning arborescences, branchings and forests in $K_n$ (with the restriction that at least a given set of vertices are internal vertices). We refer to the Appendix for the exact expressions and proofs.

4 The information content and inferring the background distribution

In the FORSIED framework, the Information Content (IC) of a pattern is defined as the negative log probability of the pattern being present in the data. The background distributions P for all prior belief types discussed in this paper have the property that P factorizes as a product of independent Bernoulli distributions,⁵ one for each possible edge $e \in V\times V$ (see Sect. 4.1). Hence the IC of a connecting subgraph C—whether it is a tree, arborescence, branching or forest—with edges $E_C$ decomposes as

$$\begin{aligned} \text {IC}(C) = -\text {log}\left( \displaystyle \prod _{e \in E_C} \text {Pr}(e)\right) = \displaystyle \sum _{e \in E_C}\text {IC}(e), \end{aligned}$$

(1)

where we defined the IC of an edge e to be $\text {IC}(e) = -\text {log}(\text {Pr}(e))$, with $\text {Pr}(\cdot )$ denoting the probability under the background distribution P.

As mentioned in Sect. 2.3, P is computed as the maximum entropy distribution subject to the prior beliefs as constraints. Here we discuss how this can be done efficiently for an important class of prior beliefs, i.e., when the user expresses prior beliefs on the density of sets of edges in a graph. In this manner, we are able to model a wide variety of prior beliefs a user has on a network. Some examples:

• In a friendship network, people with similar age/education/location are more likely to be friends.

• In a paper citation network, the number of papers citing a paper with an equal or higher publication year is very low (i.e., the network is essentially a DAG).

• Search engines (e.g., Google, Bing) are hubs in the WWW graph.

• In some social networks, vertices tend to be connected to other vertices that have similar degree values (assortative mixing).

Section 4.1 discusses how the background distribution is formally inferred. However, in many practical cases the number of prior beliefs is simply too large to do this efficiently. To avoid these situations, Sect. 4.3 introduces a sufficient condition to exploit symmetry in the optimization process. Section 6 provides a fast heuristic that implements the ideas of Sect. 4.3. Finally, in Sect. 4.2 discusses what can be done when the stated prior beliefs do not accurately reflect the actual prior beliefs.

In a first reading, Sects. 4.3 and 4.2 can safely be skipped, as they are more technical in nature and not essential for the reader to understand the logic of the main contributions in this paper.

4.1 Prior beliefs on the density of sets of edges

This section discusses the case of fitting the maximum entropy model over the set $\mathcal {X}=\{0,1\}^{n}$, which trivially extends to fitting the model over the set of rectangular binary matrices $\{0,1\}^{n\times n}$ (i.e., the set of all possible graphs over n vertices). The main reason for this is notational simplicity. Let $\mathbf x =(\mathbf x _1,\ldots ,\mathbf x _n)$ be some element in $\mathcal {X}$. We are interested in efficiently inferring the MaxEnt distribution over $\mathcal {X}$, subject to a special class of linear constraints. The types of constraints we consider are in the form of

$$\begin{aligned} \displaystyle \sum _\mathbf{x \in \mathcal {X}} P(\mathbf x ) \displaystyle \sum _{i \in S} \mathbf x _{i} = c, \end{aligned}$$

(2)

where $S \subseteq \{1,\ldots ,n\}$ and c is a specified value. These constraints can be regarded as the formalization of certain expectations the user has about the data. Consider m such constraints, with $S_k$ denoting the associated set of indices and $c_k$ the associated specified expected value, for $k \in \{1,\ldots ,m\}$. Note that these specified values $c_k$ could represent the actual sum of the elements in the sets $S_k$, as present in the actual data (as we will commonly do in the experiments). The MaxEnt distribution is found by solving

$$\begin{aligned} \displaystyle \mathop {{\mathrm{arg\, max}}}\limits _{P(\mathbf x )}&- \displaystyle \sum _\mathbf{x \in \mathcal {X}} P(\mathbf x )\log P(\mathbf x ), \nonumber \\ \text {s.t.}&\displaystyle \sum _\mathbf{x \in \mathcal {X}} P(\mathbf x ) \displaystyle \sum _{i \in S_k} \mathbf x _{i} = c_k, \nonumber \\&\displaystyle \sum _\mathbf{x \in \mathcal {X}} P(\mathbf x ) = 1. \end{aligned}$$

(3)

The resulting distribution will be a product of independent Bernouilli distributions, one for each $\mathbf x _{i}$ (De Bie 2011b, Section 3):

$$\begin{aligned} P\left( \mathbf x \right) =\displaystyle \prod _{i=1}^n\dfrac{\exp \left( \left( \sum _{k: i \in S_k}\lambda _k\right) \mathbf x _i\right) }{1+\exp \left( \sum _{k: i \in S_k}\lambda _k\right) }, \end{aligned}$$

(4)

where $\lambda _k$ is the Lagrange multiplier associated with the constraint on the set $S_k$. Note that we allow $\lambda _k \rightarrow \pm \infty$, in order to have $P(\mathbf x ) = 0 \text { or } 1$, as can be the case with certain constraints. The success probability of each of these Bernouilli distributions is given by

$$\begin{aligned} \text {Prob}\left( \mathbf x _{i}=1\right) = \dfrac{\exp \left( \sum _{k: i \in S_k}\lambda _k\right) }{1+\exp \left( \sum _{k: i \in S_k}\lambda _k\right) }, \end{aligned}$$

(5)

The parameters $\lambda _1,\ldots ,\lambda _m$ are inferred by minimizing the (convex) Lagrange dual function, as given by:

$$\begin{aligned} L(\lambda _1,\ldots ,\lambda _m) = \displaystyle \sum _{i=1}^n \log \big (1+\exp \big (\sum _{k: i \in S_k}\lambda _k\big )\big ) - \displaystyle \sum _{k=1}^m \lambda _kc_k \end{aligned}$$

(6)

The optimal values of the parameters can be found by standard methods for unconstrained convex optimization, such as Newton’s method. Newton’s method requires solving a linear system with computational complexity $\mathcal {O}(m^3)$ per iteration. Clearly, the number of parameters to be optimized over is crucial for the speed of convergence. For large databases and cases where $m=\mathcal {O}(n)$, the optimization quickly becomes unfeasible. However, in certain (practical) cases we can reduce the complexity by beforehand identifying Lagrange multipliers that have an equal value at the optimum of (6). The strategy is then to equate all these Lagrange multipliers, and form a reduced model with a smaller number of variables, and proceed to apply Newton’s method on this reduced model. Section 4.3 discusses a way to identify these equal Lagrange multipliers.

4.2 What if there is a mismatch between the stated and actual prior beliefs?

It may be infeasible in practice to sufficiently accurately state a user’s prior beliefs. If the discrepancy is too large, the pattern with highest SI may not actually be the most interesting one to the user. There are two easy ways of mitigating this risk, which we briefly discuss here for completeness.

The first approach is to find the most interesting pattern subject to a range of different background distributions. E.g. one could experiment with adding the degree constraints or not.

The second approach is to mine the top-k most interesting patterns. As discussed by De Bie (2011a), mining a set of top-k non-redundant patterns can be done iteratively, yielding a $1-1/e$ approximation of the best set. In each iteration, we find the most interesting pattern with respect to the current background distribution, followed by a conditioning of the background distribution on the knowledge of this pattern. In the case of the present paper, the conditioning operation simply amounts to equating the probabilities of the edges or arcs covered by the pattern to one.

4.3 Identifying equivalent Lagrange multipliers

As discussed in Sect. 4.1, we are interested in finding equal Lagrange multipliers at the optimum of (6). To do so, we first look at the set M, consisting of all permutations of the tuple $(\lambda _1,\ldots ,\lambda _m)$ that leave L invariant. For notational reasons, we will denote the tuple $(\lambda _1,\ldots ,\lambda _m)$ simply as $\lambda$. A permutation $\sigma$ of $\lambda$ is denoted as $\sigma (\lambda )$. The i-th element of this tuple is denoted as $\sigma (\lambda )_i$. It is not hard to see that M is a subgroup of the group of all permutations acting on $\lambda$.

Proposition 1

The set M, together with the group operation which is the composition of two permutations, forms a group.

Proof

Proposition 2.69 from Rotman (2006) states that a finite nonempty subset of a group, that is closed under the group operation, is again a group. Now clearly, M is a finite nonempty subset (it contains the identity permutation) of the group of all permutations. It is also closed under the group operation, since $L((\sigma \cdot \pi )(\lambda ))=L(\sigma (\pi (\lambda )))=L(\pi (\lambda ))=L(\lambda )$ for any two permutations $\sigma ,\pi \in M$. $\square$

Next, we will look at the set of orbits of $\lambda$. An orbit of a Lagrange multiplier $\lambda _i$ is defined as the set of Lagrange multpliers for which there exists a permutation in M that maps them onto $\lambda _i$. More formally, it is defined as

$$\begin{aligned} \text {Orb}(\lambda _i)=\{\lambda _j: \exists \sigma \in M \text { s.t. } \sigma (\lambda )_j=\lambda _i\}. \end{aligned}$$

(7)

The set of all orbits form a partition of $\{\lambda _1,\ldots ,\lambda _m\}$. One direct observation is that if $\lambda _i$ and $\lambda _j$ are part of the same orbit, we need to have $c_i=c_j$. Lemma 1 shows how finding the orbits can directly help us to a priori recognize equal optimal Lagrange multipliers.

Lemma 1

If $\lambda _i$ and $\lambda _j$ belong to the same orbit, then there exists an optimal solution to (6) for which $\lambda _i=\lambda _j$ holds.

Proof

Suppose we have an optimal solution $\lambda$ where $\lambda _i \ne \lambda _j$. Since every $\sigma \in M$ leaves L invariant, we have at least |M| other optimal solutions. By convexity of L, this implies that $\lambda ^*=\frac{1}{|M|}\sum _{\sigma \in M}\sigma (\lambda )$ is also optimal. Now we have

$$\begin{aligned} \lambda _i^*&= \frac{1}{|M|}\sum _{\sigma \in M}\sigma (\lambda )_i \\&= \frac{1}{|M|}\sum _{\lambda _k \in \text {Orb}(\lambda _i)}\frac{|M|}{|\text {Orb}(\lambda _i)|}\lambda _k \\&= \frac{1}{|\text {Orb}(\lambda _i)|}\sum _{\lambda _k \in \text {Orb}(\lambda _i)} \lambda _k, \end{aligned}$$

where the second step follows from the fact that M is a group. We can write a similar expression for $\lambda _j^*$. Because $\text {Orb}(\lambda _i)=\text {Orb}(\lambda _j)$, we have $\lambda _i^*=\lambda _j^*$. $\square$

Lemma 1 suggests that there is a possible speedup to be gained by first searching for the orbits associated with (6), equating all Lagrange multipliers that are in the same orbit, and then optimizing the reduced model. For this method to be a significant speedup we need a) the total number of orbits to be low, and b) a fast way to (approximately) find them. For a general system of prior beliefs, finding the orbits is a difficult task. For many practical situations however, the total number of orbits is low and certain equivalences can be found by exploiting the symmetry between the prior belief constraints. Two such cases are discussed in Sect. 5. Section 6 details a fast heuristic for approximately finding the orbits in a general prior belief system.

5 Discussing two prior belief types in more detail

We discuss two realistic prior beliefs in more detail. These priors were fitted on the data that was used for the experimental evaluation in Sect. 8. Section 5.1 discusses how to efficiently model a prior of a partial or total ordering of the vertices, e.g., when a graph is a DAG. Section 5.2 shows how to model knowledge about degree assortativity, i.e., when vertices have the tendency to connect to vertices of similar degree. Both priors are in combination with a prior on the individual degrees of each vertex. We refer to van Leeuwen et al. (2016) and De Bie (2011b) for a discussion on a prior solely on the individual vertex degrees.

Fig. 4

A resulting block matrix with 3 bins $b_1, b_2$ and $b_3$. There are 5 block-diagonals $D_k$ (indicated by the same fill). For each $D_k$, we express prior beliefs on the sum of all elements in $D_k$

5.1 Prior beliefs when vertices represent timed events

If the vertices in G correspond to events in time, we can partition the vertices into bins according to a time-based criterion. For example, if the vertices are scientific papers in a citation network, we can partition them by publication year. Given these bins, it is possible to express prior beliefs on the number of edges between two bins. This would allow one to express beliefs, e.g., on how often papers from year x cite papers from year y. This is useful if, e.g., one believes that papers cite recent papers more often than older ones. We discuss the case when our beliefs are in line with a stationarity property, i.e., when the beliefs regarding two bins are independent of the absolute value of the time-based criterion of these two bins, but rather only depend on the time difference.

Given an adjacency matrix $\mathbf A$, this amounts to expressing prior beliefs on the total number of ones in each of the block-diagonals of the resulting block matrix (formed by partitioning the elements into bins), see Fig. 4 for clarification. Assuming we have k bins, there are $2k-1$ such block constraints. On top of these block constraints, we can additionally constrain the in- and out degree of each vertex. This amounts to a constraint on the sum of each row and column of $\mathbf A$. There are 2n such constraints. The MaxEnt model is found by solving (3), with $2(n+k)-1$ constraints.

Simply applying Newton’s method to minimize the Lagrange dual function would then lead to solving a linear system with computational complexity $\mathcal {O}(n^3)$ per iteration. For practical problems involving large networks, this quickly becomes infeasable. Hence we use the method described in Sect. 4.3 to speed up the optimization.

The remaining part of this section is dedicated to giving a bound on the total number of unique Lagrange multipliers. We first note that there are some obvious equivalences between Lagrange multipliers, that can be bounded in terms of the network’s sparsity. These obvious equivalences are found by observing that if two row constraints have equal c-values and belong to the same bin, then their associated Lagrange multipliers must be equivalent. This can be seen by considering the Lagrange dual function. The same argument holds for the column constraints. Let $\widetilde{m}_i$ and $\widetilde{n}_i$ be the resp. number of distinct row and column sums in bin i of the matrix $\mathbf A$. The following Lemma provides an upper bound on $\sum _{i=1}^k (\widetilde{m}_i+\widetilde{n}_i)$, i.e., the total number of free row and column variables, in terms of the number of non-zero elements of $\mathbf A$ and the number of bins k:

Lemma 1

Let $\mathbf A$ be a binary rectangular matrix and denote $s = \sum _{i,j} \mathbf A$. Then it holds that $\sum _{i=1}^k (\widetilde{m}_i+\widetilde{n}_i) \le 2\sqrt{2ks}$.

Proof

Let $s_i$ ($s'_i$) be the total number of ones in all the rows (columns) of the elements in bin i. Then the following inequalities hold (De Bie 2011b):

$$\begin{aligned} \widetilde{m}_i \le \sqrt{2s_i}, \quad \text { and }\quad \widetilde{n}_i \le \sqrt{2s'_i}. \end{aligned}$$

So we have $\sum _{i} (\widetilde{m}_i+\widetilde{n}_i) \le \sqrt{2}(\sqrt{s_1}+\ldots +\sqrt{s'_k})$. Clearly also $\sum _i s_i+s_i' = 2s$ and thus by Jensen’s inequality

$$\begin{aligned} \frac{\sqrt{s_1}+\ldots +\sqrt{s_k}+\sqrt{s_1'}+\ldots +\sqrt{s_k'}}{2k} \le \sqrt{\frac{s}{k}}, \end{aligned}$$

which proves the lemma. $\square$

Hence there will be an optimal solution that depends on at most $\sum _{i} (\widetilde{m}_i+\widetilde{n}_i)+2k-1$ unique Lagrange multipliers. Using Newton’s method for this reduced model will then require $\mathcal {O}(\sqrt{s^3k^3}+k^3)$ computations in each step, making it very efficient in many real life applications (sparse networks and a small number of bins).

Remark 1

In general, binning is not limited to timed events. Any partition of the vertices, and any prior knowledge on the connectivity between the partitions can be dealt with in a very similar way. Stationarity is not a must.

Remark 2

Discretizing time is a drawback of the chosen approach. The proposed method is just one possible way to model time dependencies as prior beliefs. However, as shown in Sect. 8, these type of “discretized prior beliefs” in most cases result in sufficiently useful trees.

Fig. 5

a A 4 x 4 adjacency matrix with constraints on the connectivity of each vertex to vertices that have a difference in degree of at most 1 (indicated by the sets $S_i$). b The edge success probabilities (see (5)) according to the MaxEnt model, fitted with a combined prior on both vertex degree (row sums) and the density of the sets $S_i$. Note that although the original network was undirected, the MaxEnt model is not symmetric. However, this can easily be enforced by also incorporating the symmetric versions of the constraints

5.2 Prior beliefs on degree assortativity

Here we discuss how to model prior beliefs that a network has underlying assortative mixing, i.e., the tendency of vertices to connect to other vertices with similar characteristics (Newman 2003). In particular, we will discuss degree assortativity: when vertices have the tendency to attach to vertices of similar degree. This has been empirically observed in a lot of social networks (Newman 2002). We limit our discussion to undirected networks, but we note that degree assortativity in directed networks can be modelled in a very similar way.

Degree assortativity can be modelled—assuming the degree of each vertex is known—by expressing prior beliefs on the connectivity of each vertex to vertices that have a similar degree. Figure 5 shows an example of such a prior belief on a small undirected network of 4 vertices. For each vertex i, the set $S_i$ represents the connectivity to other vertices that have a difference in degree⁶ of at most 1. On a network of n vertices, the combined prior beliefs on the densities of the sets $S_i$, as well as on the individual degree of each vertex, leads to 2n variables to be optimized over in the Lagrange dual function, again making it infeasible in many practical scenario’s.

However, as in the previous section, we can prove that the total number of unique Lagrange multipliers will be limited in the case of sparse networks. By considering the Lagrange dual function, we observe that if two vertices i and j have equal degree and the sets $S_i$ and $S_j$ have equal density and size, then these vertices are indistinguishable to the MaxEnt model. This implies there is an optimal solution where $\lambda _i=\lambda _j$ (the corresponding Lagrange multipliers for the sets $S_i$), as well as having equal row constraint Lagrange multipliers. In fact, these are the only equivalences that can occur between Lagrange multipliers. Similarly as in the proof of Lemma 1, one can show that the total number of free variables is $\mathcal {O}(s^{3/4})$. Using Newton’s method for this reduced model will then require $\mathcal {O}(s^{9/4})$ computations in each step, making it quite efficient in the case of sparse networks.

6 A fast heuristic for identifying equivalent Lagrange multipliers

In Sect. 5, we discussed two realistic prior belief models and showed that some equivalences can be found by simply exploiting symmetry in the sets of constraints associated with these prior beliefs. However, there could be even more equivalences than the ones discussed in Sects. 5.1 and 5.2. Moreover, there could be practical cases where the prior beliefs are slightly different, and thus breaking symmetry. Hence it is in our interest to design a method that identifies orbits in a general prior belief system. This section provides a fast heuristic for (approximately) finding the orbits associated with (6), by transforming the problem to a graph automorphism problem.

Given L, as defined by (6), we construct a weighted undirected graph G as follows. The vertices are $V(G)=\{v_1,\ldots ,v_n\}\cup \{\lambda _1,\ldots ,\lambda _m\}\cup \{u\}$. There is an edge between $v_i$ and $\lambda _k$ if $\lambda _k$ occurs in the i-th term of the summation in (6). These edges all have weight $\infty$. Furthermore, all the $\lambda _k$ are connected to u, with weights $c_k$. We refer to Figure 6 for an example.

Now given this graph G, we are interested in the automorphisms of G, i.e., the permutations $\sigma$ of V(G) such that a pair of vertices (i,j) are connected if and only if $(\sigma (V(G))_i,\sigma (V(G))_j)$ are connected. This group of automorphisms naturally defines an equivalence relation on V(G) by saying that $i\sim j$ if and only if there exists an automorphism on G that maps i to j. The graph G is constructed in such a way that no $\lambda _k$ can be equivalent to any $v_i$ or u. It is clear now that finding the orbits of L is the same as identifying equivalent $\lambda _k$ vertices.

Fig. 6

a A 2 x 2 adjacency matrix with constraints on the density of the sets of edges $S_1, S_2$ and $S_3$. The Lagrange dual (6) reduces to $L(\lambda _1,\lambda _2,\lambda _3)=f(\lambda _1+\lambda _2)+f(\lambda _1)+f(\lambda _3)+f(\lambda _2+\lambda _3)-c_1\lambda _1-c_2\lambda _2-c_3\lambda _3$, with notation $f(\cdot )=\log (1+\exp (\cdot ))$. For generic $c_1=c_3$ and $c_2$, the orbits are $\{\lambda _1,\lambda _3\}$ and $\{\lambda _2\}$. b The constructed graph G used to identify the orbits of L. If $c_1=c_3$ there is an automorphism mapping $\lambda _1$ to $\lambda _3$, and hence they are part of the same orbit

In general, determining the automorphism group of a graph is equivalent to the graph isomorphism problem. For the latter problem, it is not known whether there exists a polynomial time algorithm for solving it. Hence, we resort to using a simple heuristic that was previously introduced in (Everett and Borgatti 1988) and used in (Mowshowitz and Mitsou 2009).

The algorithm exploits the fact that two vertices in a graph can only be equivalent if they share the same structural properties, such as having the same degree. Roughly, the procedure goes as follows:

• 1. Start by setting all $\lambda _k$ vertices to be equivalent.

• 2. Run a number of tests (based on structural properties) to distuinguish between vertices. If two vertices have different outcomes of a test, they are in different equivalence classes.

Naturally, the tests need to be computed in reasonable (polynomial) time. In this work we will use the following three structural tests, calculated for each vertex $\lambda _k \in (\lambda _1,\ldots ,\lambda _m)$:

• T1. The degree of $\lambda _k$.

• T2. The corresponding $c_k$-value, i.e., the weight of the edge $(\lambda _k,u)$.

• T3. A sorted list of c-values of the neighbors of the vertices $v_i$ that are connected to $\lambda _k$.

Applying this procedure to the example in Figure 6, assuming a case where $c_1=c_2=c_3$, yields the following results

• a) The partition is initialized as $P=\{\lambda _1,\lambda _2,\lambda _3\}$.

• b) T1 gives (3, 3, 3) and does not further partition P.

• c) T2 gives $(c_1,c_2,c_3)$ and does not further partition P.

• d) T3 gives $([c_1,c_1,c_2], [c_1,c_2,c_2,c_3], [c_3,c_3,c_2])$. Because $c_1=c_3$, this test further partitions P into $P=\{\{\lambda _1,\lambda _3\},\{\lambda _2\}\}$.

Remark 3

The actual equivalence classes can only be finer partitions than those found by the heuristic. The heuristic may falsely conclude that two Lagrange multipliers are equal. However, we emphasize that this is in general not a major problem for the MaxEnt model. Equating two Lagrange multipliers without justification is equal to replacing the respective constraints in (3) into a new constraint on the sum of the original constraints. It thus becomes a relaxation of the original MaxEnt problem, with relaxed constraints. The patterns that are found to be interesting can potentially still be explained by the original prior beliefs.

Remark 4

We note that other well-known graph automorphism heuristics can be used as well, such as the Weisfeiler-Lehman procedure (Fürer 2017). The main advantages of the heuristic discussed above is that it is fast for our purposes, and it correctly identifies all the unique Lagrange multipliers that were discussed in Sect. 5. We refer to Sects. 8.1 and 9 for a more detailed discussion.

7 Algorithms for finding the most interesting trees

Section 7.1 discusses the how to find a maximally subjectively interesting connecting arborescence, i.e., the solution to Problem 1. Our proposed methods for solving Problems 2–4 are direct applications of our solution to Problem 1, and are discussed in Sect. 7.2.

Problem 1 is closely related to the NP-hard problem of finding a minimum Steiner arborescence (Korte and Vygen 2007; Charikar et al. 1998), defined for weighted directed graphs as a minimal-weight arborescence with a given set of query vertices as its candidate leaves. The connection with this well-studied problem allows us to show that Problem 1, which is the problem of finding an arborescence (spanning all the query vertices) with maximum SI, is NP-hard. Indeed, for constant edge weights (e.g., if the prior belief is the overall graph density), the SI of an arborescence will be a decreasing function of the number of vertices in the tree. Hence for this special case, our problem is equivalent to the minimum Steiner arborescence problem with constant edge weights, which is NP-hard. For non-constant background models Problem 1 will optimize a trade-off between the IC and the DL of an arborescence. In most cases, this will amount to looking for small arborescences with highly informative edges.

There are a number of algorithms that provide good approximation bounds for the directed Steiner problem (Charikar et al. 1998; Melkonian 2007; Watel and Weisser 2014), and this problem has also been studied recently in the data mining community (e.g., Akoglu et al. 2013; Rozenshtein et al. 2016). However, Problem 1 is only equivalent to the directed Steiner problem in the case of a uniform background distribution, i.e., when the IC of the edges is constant.

A good overview of the currently known solutions to all sorts of variants to the Steiner tree problem is given by Hauptmann and Karpiński (2013). Problems 1–4 are not equivalent to any of these problems, because in general the subjective interestingness of a tree does not factorize as a sum over the edges. For this reason we propose fast heuristics for large graphs, that perform well on different kinds of background distributions. A Python implementation of the algorithms is available at https://bitbucket.org/ghentdatascience/interestingtreespublic/.

7.1 Proposed methods for finding arborescences

Our proposed methods for finding arborescences all work in a similar way. We apply a preprocessing step, resulting in a set of candidate roots. Given a candidate root r, we build the tree by iteratively adding edges (parents) to the frontier⁷—initialized as $Q {\setminus } \{r\}$—, until frontier is empty. We exhaustively search over all candidate roots and select the best resulting tree. The heuristics differ in the way they select allowable edges. The outline of SteinerBestEdge is given in Algorithm 1.

Preprocessing All of the proposed heuristics have two common preprocessing steps. First we find the common roots of the vertices in Q up to a certain level k, meaning we look for vertices r, s.t. $\forall q \in Q: \text {SPL}(q, r) \le k$, with SPL$(\cdot )$ denoting the shortest path length. This can be done using a BFS expansion on the vertices in Q until the threshold level k is reached. Note that query vertices are also potential candidates for being the root, if they satisfy the above requirement.

Secondly, for each r we create a subgraph $H \subset G$, consisting of all simple paths $q\rightsquigarrow r$ with $\text {SPL}(q,r)\le k$, for all $q \in Q$. This can be done using a modified DFS-search. The number of simple paths can be large. However, we can prune the search space by only visiting vertices that we encountered in the BFS expansion, making the construction of H quite efficient for small k.

SteinerBestEdge (s-E) Given the subgraph H, we construct the arborescence working from the query vertices up to the root. We initialize the frontier as $Q {\setminus } \{r\}$, and iteratively add the best feasible edge to a partial solution, denoted as Steiner, according to a greedy criterion. The greedy criterion is based on the ratio of the IC of that edge to the DL⁸ of the partial Steiner that would result from adding that edge. This heuristic prefers to pick edges from a parent vertex that is already in Steiner, yielding a more compressed tree and thus a smaller DL.

Fig. 7

Example of why look-ahead is needed to ensure the returned tree has depth as most k. If $k=2$, the only valid tree is $(Q_1,R)(Q_2,Q_1)$. Initially, the frontier is $\{Q_1,Q_2\}$ and X is a candidate parent for $Q_1$ because there is a path $Q \rightsquigarrow R$ of at most length 2. Yet, adding the dashed edge violates the shortest path constraint for $Q_2$

Fig. 8

Example of why look-ahead is needed for sets of edges. For $k=3$, neither of the two dashed edges violate the depth constraint—they are part of a valid tree—, but together they indirectly violate the shortest path constraint for $Q_1$. Regardless of which parent is chosen for A, the path from $Q_1$ to R has length 4

Algorithm 2 checks if an edge is feasible by propagating its potential influence to all the other vertices in H. The check can fail in two ways. First, the addition of an edge could yield a Steiner tree with depth $> k$, see Figure 7 for an example. Secondly, the addition of an edge may lead to cycles in Steiner. Cycles are avoided by only considering edges (s, t) that do not potentially change $\text {SPL}(t, r)$. If $\text {SPL}(t, r)$ would change, the shortest path—given the current Steiner—from s to r is not along the edge (s, t) and hence for all $f \in frontier$ we always have 1 feasible edge to pick (i.e., an edge that is part of a shortest path $f \rightsquigarrow r$). One way to select the best feasible edge is to first sort the edges according to the greedy criterion. Then try the check from Algorithm 2 on this sorted list (starting with the best edge(s)), until the first success, and add the resulting edge to Steiner. Algorithm 2 will also return an updated shortest path function NewSP, containing all the changes in $\text {SPL}(n, r)$ for $n \in H$ due to the addition of that edge to Steiner. After performing the necessary updates on the SP function, and the frontier, parents and level sets, we continue to iterate until frontier is empty.

SteinerBestIC (s-IC) Instead of adding 1 edge at a time, this heuristic adds multiple edges at once. We look for the parent vertex that (potentially) adds the most total information content of allowable edges to the current Steiner. However, given such a parent vertex, it not always possible to add multiple edges, see Figure 8. Instead we sort the edges coming from such a parent vertex according to their IC, and iteratively try to add the next best edge to Steiner.

SteinerBestIR (s-IR) A natural extension of SteinerBestIC is to actually take in account the DL of the partial Steiner solution, as we did in SteinerBestEdge. SteinerBestIR favors parent vertices that are already in Steiner, steering towards an even more compressed tree.

SteinerBestEdgeBestIR (s-EIR) Our last method simply picks the single best edge coming from the best parent, where the best parent is determined by the same criteria as in SteinerBestIR. In general this will pick a locally less optimal edge than SteinerBestEdge, but it will pick edges from a parent vertex that has lots of potential to the current Steiner solution.

Correctness of the solutions The following theorem states that all the heuristics indeed result in a tree with maximal depth $\le k$.

Theorem 2

Given a non-empty query set Q, a candidate root r and a depth $k \ge 1$. In all cases all four heuristics will return a tree with depth $\le k$.

Proof

In all cases the proposed heuristics return a tree rooted at r with depth $\le k$. We call a partial forest solution Steiner valid, if for all leaf vertices $l \in Steiner: \text {SPL}(l,r|Steiner) \le k$, where $SPL(\cdot |Steiner)$ denotes a shortest path length given the partial Steiner solution. Note that the initial Steiner is valid, due to the way the subgraph H was constructed. It is always possible to go from one valid Steiner solution to another valid one, by selecting an edge (incident to a frontier vertex) along a shortest path—given we have Steiner—from r that frontier vertex. This will result in an unchanged SPL for all other vertices (in particular the leaf vertices), and hence remains a valid Steiner. If we have n frontier vertices, we have at least n such valid edges to pick from. Hence, all of the heuristics have at least $n\ge 1$ valid edges to pick from. The process of adding edges is finite, and will eventually result in an arborescence rooted at r with depth $\le k$. $\square$

7.2 Proposed methods for finding trees, branchings and forests

In this section we will sketch the outline of our methods for finding connecting trees and forests in an undirected network, as well as finding connecting branchings in a directed network. They all make direct use of the proposed methods for finding arborescences, as described in Sect. 7.1. We transform an undirected graph G to a directed graph $G'$ by replacing each undirected edge $\{u,v\}$ by two oppositely directed edges (u, v) and (v, u).

Trees Given the transformed directed graph $G'$, we consider the candidate root set $R = \{q \in Q: SPL(q,x) \le \left\lfloor {\frac{k}{2}}\right\rfloor , \forall x \in Q\}$. For each candidate root $r \in R$, construct H by finding all simple paths from $Q {\setminus } \{r\}$ to r and apply one of the methods Sect. 7.1. Take the r that gives the arborescence with maximal SI. Transform the resulting arborescence back to a tree by removing the directionality of the edges. The result will be a tree $T=(V(T), E(T))$ with $\text {leaves}(T) \subset Q \subset V(T)$ and depth $\le k$.

Branchings Find all vertices that are within a distance k from all $q \in Q$ (by using a BFS search). Let H denote the induced subgraph by these vertices on G. Then add vertex r to H, and edges (x, r) $\forall x \in H$. Given H, apply one of the methods in Sect. 7.1 with candidate root r and depth $k+1$. Remove the vertex r and all edges to r. The result will be a branching $B=(V(B), E(B))$ with $\text {leaves}(B) \subset Q \subset V(B)$ and depth $\le k$.

Forests Given the transformed directed graph $G'$, add a vertex r and edges (q, r) $\forall q \in Q$. Now construct H by finding all simple paths from Q to r with max. level $\left\lfloor {\frac{k}{2}}\right\rfloor +1$. Given H, apply one of the methods in Sect. 7.1. Remove the directionality of the edges, the vertex r and any edges to r. The result will be a forest $B=(V(F), E(F)$ with $\text {leaves}(F) \subset Q \subset V(F)$ and depth $\le k$.

Remark 5

A combination of these heuristics can also be used as a heuristic, e.g. for finding forests, one can use the algorithm described above to find an initial partition of the query set, after which one can use a method for finding trees on each partition.

8 Experiments

We evaluated the performance and utility of our proposed methods. Section 8.1 discusses the efficiency of fitting different background models on a variety of different datasets. In particular, it shows the efficiency of the algorithm described in Sect. 4.3 for fitting the prior beliefs that were discussed throughout Sect. 4. Given such a prior belief model, Sects. 8.2 and 8.3 discuss the performance of the tree finding methods, both in accuracy and in speed. Section 8.4 discusses to which extent the resulting trees are indeed dependent on the prior beliefs. Finally, Sect. 8.5 shows some visual examples for subjective evaluation, and a comparison with related methods. All experiments were done on a PC with an Intel i7-7700K CPU and 32 GB RAM.

8.1 Fitting the different background models

This section is dedicated to showing the efficiency of fitting the MaxEnt model on a number of large networks, by making use of the heuristic for a priori identifying equal Lagrange multipliers (Sect. 4.3). The second last column in Table 1 shows the runtime for computing the heuristic. The last column indicates the time to run Newton’s method for finding the optimum of the (reduced) Lagrange dual function (6). The third column shows the number of unique Lagrange multipliers as found by the heuristic. We note that for the prior beliefs under consideration, the heuristic was able to correctly identify all the unique Lagrange multipliers (e.g. in the case of bins, this is true because the upper bound from Sect. 5.1 on the number of equivalences reaches equality). Thus, Remark 3 did not apply here, although this is not to be expected in all cases.

Clearly, Table 1 shows that even very large networks can be fitted efficiently with these kind of prior beliefs. In comparison with the DBLP⁹ dataset, the roadNet-CA¹⁰ dataset requires less than 10% of fitting time, even though it is a larger network. This can be explained by looking at the number of unique degrees in the network, which is crucial for the number of unique Lagrange multipliers and hence total fitting time: roadNet-CA has only 11 unique degrees, whereas DBLP has 199. The NBER¹¹ dataset consists of citations between U.S. patents in the timeframe 1975-1999. The patents can be binned according to categories such as ‘Chemical’,‘Computers & Communications’, etc., and then further refined into subcategories such as ‘Gas Chemical’, ‘Coating Chemical’, etc. This leads to resp. 6 and 59 bins. Expressing prior beliefs on the number of citations between categories can then be done similarly as in Sect. 5.1. The ACM citation dataset consists of research papers in the field of computer science. The oldest paper is a seminal paper of C.E. Shannon from 1938, the more recent papers are from 2016. Binning per 5 years leads to 16 bins, binning each year separately leads to 78 bins. Table 1 shows the rather drastic influence on the number of bins on the total fitting time. We refer to Sect. 5.1 for a complexity discussion.

Table 1 Fitting times for the different prior belief models

8.2 Testing the relative performance of the heuristics

Since the algorithms for finding trees, forests and branchings directly make use of the heuristic for finding aborescences, we only test the different heuristics that were proposed for finding arborescences. We tested the performance on the ACM, DBLP and Amazon datasets, all fitted with a different background model as indicated by Table 1. We randomly generated a number of queries and compare our methods with the optimal arborescence (over a large pool of arborescences) and the average over this pool.

The experiment setting is similar to Akoglu et al. (2013). To generate a set of n query vertices we used a snowball-like sampling scheme. We randomly selected an initial vertex in the graph. Then, we explore $n' < n$ of its neighbors, each selected with probability s. For each of these vertices we continue to test $n'$ of its neighbors until we have n selected vertices. From this query set we randomly select a valid common root within a maximum distance k.

To have a baseline, we tried to find the arborescence with maximal SI by exhaustively enumerating all possible arborescences. To keep this search feasible, we stopped adding to the enumeration once we have checked 10, 000, 000 arborescences¹² per random query. The enumeration of the arborescences is done in a random manner, by looking at randomly shuffled cartesian products of paths from each query to the root, and only keeping those cartesian products that form a valid tree. We tested 3 different query sizes $\{4,8,12\}$, and for each query size, we generated 500 queries with $k=4$, $n'=4$ and $s=0.8$.

Table 2 shows the average size of these pools of trees that were found in the data. Over each pool we took the tree with maximal SI and the average SI over all trees as a baseline.

Table 2 The average number of arborescences per query that were found in the data and used for the comparison in Fig. 9

Fig. 9

Relative performance of the proposed heuristics for finding arborescences

Figure 9 shows a boxplot of the interestingness scores of the tree-building heuristics (relative scores to the optimal arborescence interestingness in the pool) versus query size. All four heuristics clearly are better strategies than randomly selecting an arborescence (the Avg. case). s-IR outperforms s-IC in all cases, which makes sense because s-IC has no regard for the DL of the tree. s-IR, s-E and s-EIR have comparable performance for smaller query sizes, but s-IR seems to be the best option for larger query sizes. Figure 10 shows the average runtimes of the heuristics for the different datasets. There is negligible difference between the heuristics, since the main bottleneck is finding all the simple paths from the queryset to the root (in all cases taking up more than 99% of the runtime). In comparison, for query sizes $\{4,8,12\}$, on the Amazon dataset it took on average resp. 13s, 27s and 31s to enumerate the arborescences from Table 2, which is at least a 100 times slower than running any heuristic. We expect a linear relationship between the query size and the runtime for a fixed depth k (since for each query vertex all simple paths to the root are calculated separately). Interestingly enough, there is a large difference in runtime between the Amazon and DBLP datasets, yet the graphs are of comparable sizes (see Table 1).

Fig. 10

Average runtime for finding arborescences (s-IR heuristic) of fixed depth $k=4$ and varying query sizes. There is negligible difference between the heuristics, since the main bottleneck is finding all the simple paths

8.3 Scalability with varying tree depth

In a second timing experiment, we tested the scalability of the tree finding algorithms for increasing depth of the connecting trees. As discussed in Sect. 8.2, the running time linearly increases for fixed depth and increasing query size. However, this is not to be expected for fixed query size and increasing depth, since the running time for finding all simple paths with length $\le k$ depends exponentially on k. We used the Amazon dataset, fitted with a prior on individual degrees. For finding (directed) arborescences and branchings, we considered each undirected edge as consisting of two directed edges. Queries were generated similarly as in Sect. 8.2, setting the query size $n = 14$, $n' = 4$ and $s = 0.8$. For each depth k, we generated 50 queries and calculated the time it took to find a connecting arborescence, tree, branching and forest. The s-IR heuristic was used as a basis for all the algorithms. Figure 11 shows the average over these 50 queries. For $k \ge 12$, the search for finding arborescences quickly became unfeasible and was terminated early. Finding branchings seems to scale particularly well, which is because there is no explicit procedure required to find all simple paths (see Sec. 7.2). We conclude that most of our algorithms scale rather poorly for larger depths, however one can argue that a user will be seldom interested in a connecting tree having a depth that is greater than the query size.

Fig. 11

Average runtime for finding arborescences, trees, forests and branchings for fixed query size $n=14$ and varying tree depth k on the Amazon dataset

8.4 Testing the influence of the prior belief model on the resulting trees

Here we evaluate the outcome of our tree finding methods w.r.t. the different prior belief models. We tested to what extent the heuristics take into account the prior belief model the user has about the data. To do so, we randomly generated queries similarly as in Sect. 8.2. For each dataset, we generated 200 queries of size $n=8$ and depth $k=8$.

The Amazon dataset was fitted with two different prior belief models: one on overall graph density and one on the degree of each individual vertex. According to the MaxEnt model, a prior on overall graph density implies that each edge is equally interesting. In this case the heuristics will look for the smallest possible connecting tree. A prior on individual vertex degrees implies that in general, a connection between two high degree vertices is more likely —and hence less interesting—than a connection between two low degree vertices. We expect this to be reflected in the resulting trees. Table 3 shows the average degree of the vertices in the connecting trees, for the two different priors. There is a significant difference between the two prior belief models, confirming the claim that a prior on individual vertex degree results in a preference for low degree vertices as connectors between the query vertices.

Table 3 Influence of the prior belief model on the average degree of the vertices in randomly generated forests in the Amazon dataset

The ACM citation network was fitted with an individual vertex degree prior, and an additional prior on the difference in publication year between citing papers (see Sect. 5.1). In general, citations between papers with a large difference in publication year are less common and hence more interesting. Figure 12 shows a histogram plot of the difference in publication year between citing papers in the ACM citation network. Hence we expect our algorithms to incorporate this knowledge and prefer citations to older papers. This is confirmed by Table 4.

Fig. 12

Difference in publication year between citing papers in the ACM v8 citation network

Table 4 Influence of the prior belief model on the average difference in publication year of all the citing papers in randomly generated branchings in the ACM dataset

Table 5 Influence of the prior belief model on the average difference in vertex degree of all the connected vertices in randomly generated trees in the DBLP dataset

Lastly, the DBLP co-authorship network was fitted with an individual vertex degree prior, and an additional prior on the network’s degree assortativity. As reported by Newman (2002), co-authorship networks have the tendency to be assortitive, i.e., high degree vertices tend to be connected to high degree vertices and low degree vertices to low degree vertices. The DBLP dataset has a positive assortativity coefficient¹³ of 0.27, confirming this observation. Hence, we expect our algorithms to incorporate this knowledge and preferring links between authors that have a large difference in degree. This is confirmed by Table 4, showing the significant influence of the prior belief model on the average difference of the degrees between all connections in a tree (Table 5).

8.5 Subjective evaluation

In a first visualization, we queried the three most recent KDD best paper award winners that are present in the ACM citation network. Figure 1 shows the resulting connecting arborescences, for 3 different types of prior beliefs. For all prior beliefs, the connecting arborescences are in direct contrast with the expectations a user has on the network. We compare¹⁴ our methods with the known Dot2Dot-MinArborescence algorithm (Akoglu et al. 2013; Horng Chau et al. 2012). Interestingly, the Dot2Dot algorithm does not find a connection between the papers: the solution consists of the 3 papers and no edges between them. The Dot2Dot algorithm took about 50h to complete, whereas our method finished in under a minute for all prior beliefs.

Secondly, we compare our methods on the Karate dataset (Zachary 1977). The Karate dataset is a small social network of a university karate club. The network consists of two predefined communities, simulating a conflict of leadership that arose in the club. Figure 13 shows the resulting connecting trees when querying one complete community (indicated by green), for a number of different types of prior beliefs. Figure 13a shows the result for an overall graph density prior. Each connection is equally informative, and hence the tree is formed by using a high degree connector as one of the central vertices Figure 13b shows the result for an individual degree prior. Connections involving high degree vertices are expected, and hence less interesting. The tree is now constructed by using a central vertex having a lower degree than the central vertex in (a). Figure 13c shows the result if there is a combined prior on individual degree and on the density of the connectivity inside each community. Edges between the two communities are now preferred, since they are less common than edges inside communities and thus less expected. Moreover, because of the prior on individual vertex degree, edges involving high degree vertices are again avoided if possible. Figure 13d shows the result of the Dot2Dot-MinArborescence algorithm. This method also prefers low degree vertices as internal vertices in the connecting tree, similarly as in (b). Since the network is small, there is negligible difference in running time between the methods.

Fig. 13

A comparison of our methods with the existing Dot2Dot algorithm on the Karate dataset. As a query we took one of the 2 predefined communities present in the network (indicated by green). a The resulting connecting tree for the s-IR heuristic if there is a prior belief on the overall graph density. b The resulting connecting tree for the s-IR heuristic if there is a prior belief on the individual vertex degrees. c The resulting connecting tree for the s-IR heuristic if there are prior beliefs on individual vertex degree, and additionally, on the density of the connectivity inside each community. d The result of the Dot2Dot-MinArborescence algorithm

Lastly, to compare speed and interestingness, we repeat an experiment from Akoglu et al. (2013). The DBLP-4-Area dataset¹⁵ is a subset of DBLP, containing meta info about the specific conferences where authors have published. In their example, they queried the top 5 authors from both NIPS (machine learning) and PODS (database systems). The result of their Dot2Dot-MinArborescence algorithm is shown in Figure 14c. Their method partitions the query set into two parts, suggesting that the authors from each community are sufficiently far apart. Our methods recover the same partitioning. Figure 14a shows the result of our method with a prior on overall graph density. Since there is no regard for the degree of each author, the connection is formed using highly collaborative authors such as ‘Michael I. Jordan’, ‘C. Papadimitriou’ and ‘Christopher K. I. Williams’. Figure 14b shows the result of our method with a prior on individual vertex degree. Connections between highly collaborative authors are now expected and thus less interesting. The forest contains lesser known authors such as ‘François Rivest’, a former PhD student from ‘Yoshua Bengio’ and a former MSc. student of ‘Doina Precup’. The forests from Figure 14b and Figure 14c are quite similar, since both methods try to optimize a similar objective: a concise connecting forest with preferably low degree connectors. Comparing the SI of both forests, we find that their forest actually scores slightly better on our metric: 0.767 vs. 0.751. This is mainly due to our forest having one internal vertex more and thus a slightly larger description length. However, in terms of speed, the difference is more obvious. Their method needed 27,310 seconds (about 7.5h) to finish, whereas we needed about 10s to fit the background model and 22s to find the connecting forest.

Fig. 14

Querying the top 5 authors (red square labels) from both NIPS (blue hull) and PODS (red hull). Vertex degrees are indicated between brackets. a The connecting forest using the s-IR heuristic, with a prior on overall graph density. b The connecting forest using the s-IR heuristic, with a prior on individual vertex degrees. c The connecting forest from the Dot2Dot-MinArborescence algorithm

9 Related work

Finding connecting subgraphs between a set of vertices in a graph is a relatively novel problem. The most related algorithmic result is the Dot2Dot algorithm of Akoglu et al. (2013). They study the problem of finding a good partitioning and connection structure within each part on undirected graphs for a given set of query vertices. There are some differences in philosophy. Their work assumes an encoding scheme, where both the sender and user know the graph structure. The task is then, by using the graph connectivity, to find a succinct encoding of the query vertices. They rely on the Minimum Description Length principle (Rissanen 1978) to find such a description. The resulting patterns happen to be forests: it only costs extra bits to refer a vertex that is already encoded in a pathway. In this work, we assume the edges of the graph are unknown, and we are interested in learning the graph’s connectivity, especially in relationship to the query set. We refer to Sect. 2.2 as to why we choose tree structures as data mining patterns. Our approach is more flexible; we are able to incorporate user-defined prior knowledge about the graph, we have a parameter that controls the depth of the trees and our methods work for both undirected and directed graphs.

Other closely related work includes the work of Faloutsos et al. (2004), which adressed the problem of finding a so called “Connection Graph”, i.e., a small interesting subgraph that connects a pair of vertices. This was later extended by Ramakrishnan et al. (2005) and Sevon and Eronen (2008) to find connections in multi-relational graphs. However, these connection graphs are only defined for pairs of vertices and are in general not tree-structured.

Langohr and Toivonen (2012) were interested in finding a set of “relevant and non-redundant vertices” in relationship to a set of query vertices. The returned vertices should have a high proximity to the query set (relevance), but far away from each other (non-redundant). Moreover, it is possible to specifiy the irrelevance of a vertex, because certain relationships regarding that vertex are already expected. Although similar in intent, there are some differences with our work. Their idea of prior knowledge seems to be in regard to vertices, whereas ours is based on edge connectivity. Secondly, they are not concerned with returning tree-structures, but rather with returning a list of vertices.

Zhou et al. (2010) introduced the idea of simplifying weighted networks by pruning the least important edges from them. They assume the number of edges to be removed is a (fixed) parameter, and hence the result will not always be a tree. Moreover, they are not concerned with a set of query vertices or a subjective interestingness measure (the edges are scored by a path quality function, indicating how relevant a path is to the overall graph connectivity). Instead, their aim is to maintain good overall graph connectivity after the pruning.

Wu et al. (2018) proposed a visual analytic system called MERCER (Maximum Entropy Relational Chain ExploRer), designed to help a user discover interesting relationships, e.g. in large text datasets. They use MaxEnt modelling to find interesting “bicluster chains” as a summary of how different entities in a document are related. Similarly as our work, they discuss fitting a MaxEnt model over a binary matrix, with the densities of certain tiles as constraints. They propose classical iterative scaling and conjugate gradient descent methods to infer the distribution’s parameters, limiting their approach to smaller datasets (experiments were done on 3000x3000 matrices). Roughly speaking, MERCER finds all possible paths through a bicluster that a user requests for evaluation. After that, each chain is translated into a unique set of tiles and the maxent model is used to score them. The length of the chains is not a part of the scoring process, making this a different framework than FORSIED. Instead, they let the user visually decide which chain is the most useful. Their work is focused on interactively mining multi-relational data, which is a different setting than ours.

In regards to fitting a probabilistic background model as a reflection of a user’s prior beliefs, this work is an extension of the work by De Bie (2011b) and van Leeuwen et al. (2016). Their work was limited to the case of a prior belief solely on vertex degrees. This work is an extension, showing how the MaxEnt model can be efficiently used to model prior beliefs on the densities of any particular sub-networks.

We conclude this section by discussing some related work on graph automorphism problems. Another well-known heuristic for checking graph isomorphisms is the Weisfeiler-Lehman procedure (Fürer 2017; Kersting et al. 2014). In its simplest form (usually referred to as WL[1] vertex classification), it reduces to vertex classification by coloring the vertices. Initially, all vertices are given the same color. The colors are then refined in consecutive rounds. In each round, two vertices receive a different color if the multiset of their neighbor’s colors are different in the previous round. The procedure reaches a stable coloring after at most |V| rounds. The actual equivalence classes can only be a finer partition than those found by the stable coloring, similarly as with the procedure from Sect. 6. There are 3 main reasons we chose to not use the WL[1] procedure:

• 1. The procedure from Sect. 6 is fast in practice, taking only a fraction of the total time to compute the background distribution (see Sect. 8.1).

• 2. For all the prior beliefs discussed in this paper (individual degrees, time relations, degree assortativity), the procedure was able to correctly identify all the equivalent Lagrange multipliers (see Sect. 8.1).

• 3. WL[1] needs |V| rounds in the worst-case to reach a stable coloring. Our procedure only needs 3 rounds. Moreover, WL[1] finds a coloring of all the vertices in the graph G from Sec. 6, while our procedure only finds equivalences between the $\lambda$ vertices, as this is our sole interest.

However, we do note that for more complex prior beliefs, it could be that the procedure from Sect. 6 returns a refinement that is too coarse. In these cases, WL[1] could be an alternative option, as well as the well-known practical NAUTY algorithm (McKay and Piperno 2013) which identifies the exact equivalence relationships.

10 Concluding remarks

We studied the problem of finding interesting trees that connect a user-provided set of query vertices in a large network. This is useful for example to, based on citation data, find papers that (indirectly) influenced a set of query papers, perhaps to understand the structure of an organization from communication records, and in many other settings. We defined the problem of finding such trees as an optimization problem to find an optimal balance between the inforativeness (the Information Content) and conciseness (the Description Length) of a tree. Additionally, by encoding the prior beliefs of a user, we propose how to find results that are surprising and interesting to a specific user.

We showed how the MaxEnt model can be efficiently used to model a wide range of prior beliefs, namely about the density of any particular sub-networks. This allowed us, for example, to model knowledge about a network’s degree assortativity, or to model knowledge of the (time based) partial ordering of papers in a citation network.

The computational problem solved in this paper is related to the problem of constructing a minimal Steiner arborescence. There is a long development of approximation algorithms, e.g., (Charikar et al. 1998; Melkonian 2007; Watel and Weisser 2014). Faster special-purpose approximations have also been studied in the data mining community, e.g., for temporal networks (Rozenshtein et al. 2016). However, in general our problem does not reduce to any of the known Steiner problems, since the SI of a tree does not factorize as a sum over the edges.

Future work includes the algorithmic improvement of the tree finding methods, the investigation of more complex prior beliefs and the possible applications in biology and social media.

Appendix: Counting the number of arborescences, branchings and forests

Similarly as Theorem 1, Theorems 3–5 can be proven by considering the base case $k=0$ and using the inclusion-exclusion principle.

Theorem 3

Given a set of k labeled vertices in $K_n$. There are

$$\begin{aligned} A(n,k) = \displaystyle \sum _{i=0}^k (-1)^i {{k}\atopwithdelims (){i}}(n-i)^{n-1} \end{aligned}$$

spanning arborescences in $K_n$, s.t. these k vertices are all internal vertices.

Proof

Since every spanning tree has n orientations as an arborescence (there are n choices for the root), there are $n^{n-1}$ spanning arborescencs in $K_n$. The rest of the proof follows the same steps as in the proof of Theorem 1. $\square$

Theorem 4

Given a set of k labeled vertices in $K_n$. There are

$$\begin{aligned} B(n,k) = \displaystyle \sum _{i=0}^k (-1)^i {{k}\atopwithdelims (){i}}(n+1-i)^{n-1} \end{aligned}$$

branchings in $K_n$, s.t. these k vertices are all internal vertices.

Proof

There are $(n+1)^{n-1}$ branchings in $K_n$ (Moon 1970). This can be counted in the following way. Let r be a vertex in $K_{n+1}$. The number of branchings in $K_n$ is equal to the number of spanning arborescences in $K_{n+1}$ (rooted at r), which is equal to the number of spanning trees in $K_{n+1}$, i.e., $(n+1)^{n-1}$. The rest of the proof follows the same steps as in the proof of Theorem 1, observing that there are $(n+1-i)^i$ ways to add i leafs to a branching consisting of $n-i$ vertices (every leaf can be the child of $n-i$ possible parents, or just be an isolated new vertex in the branching). $\square$

A similar argument for counting forests in $K_n$ does not hold. In fact, no nice expression for the base case $k=0$ is available. Let $f_m(n)$ be the number of forests in $K_n$, consisting of m connected components. It is shown (Rényi 1959; Moon 1970, Theorem 4.1) that

$$\begin{aligned} f_m(n) = {{n}\atopwithdelims (){m}}\displaystyle \sum _{i=0}^m \left( -\displaystyle \dfrac{1}{2}\right) ^i(m+i)i!{{m}\atopwithdelims (){i}}{{n-m}\atopwithdelims (){i}}n^{n-m-i-1}. \end{aligned}$$

Define $F_0(n) = \sum _{m=1}^n f_m(n)$. It follows that

Theorem 5

Given a set of k labeled vertices in $K_n$. There are

$$\begin{aligned} F(n,k) = \displaystyle \sum _{i=0}^k (-1)^i {{k}\atopwithdelims (){i}}(n+1-i)^{i}F_0(n-i) \end{aligned}$$

forests in $K_n$, s.t. these k vertices are all internal vertices.

Proof

Using a similar argument as in the proof of Theorem 1, and observing that there are $(n+1-i)^i$ ways to add i leafs to a forest consisting of $n-i$ vertices (each leaf can be attached to $n-i$ possible vertices, or it can be added as an isolated new vertex in the forest). $\square$

Thus, communicating an arborescence A, a branching B or a forest F (all of size n) can be done efficiently by using this many bits:

$$\begin{aligned} \text {DL}(A)&= |V|-|Q|+\log (A(n,n-|Q|)), \\ \text {DL}(B)&= |V|-|Q|+\log (B(n,n-|Q|)), \\ \text {DL}(F)&= |V|-|Q|+\log (F(n,n-|Q|)). \end{aligned}$$