Skip to main content
SpringerLink
Log in

Adaptive heterogeneous multiscale methods for immiscible two-phase flow in porous media

  • ORIGINAL PAPER
  • Published:
Computational Geosciences Aims and scope Submit manuscript

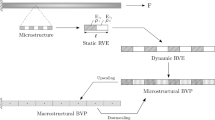
Abstract

In this contribution, we present the first formulation of a heterogeneous multiscale method for an incompressible immiscible two-phase flow system with degenerate permeabilities. The method is in a general formulation, which includes oversampling. We do not specify the discretization of the derived macroscopic equation, but we give two examples of possible realizations, suggesting a finite element solver for the fine scale and a vertex-centered finite volume method for the effective coarse scale equations. Assuming periodicity, we show that the method is equivalent to a discretization of the homogenized equation. We provide an a posteriori estimate for the error between the homogenized solutions of the pressure and saturation equations and the corresponding HMM approximations. The error estimate is based on the results recently achieved as reported by Cancès et al. (Math. Comp. 83(285):153–188, 2014). An a posteriori error estimate for vertex-centered finite volume discretizations of immiscible incompressible two-phase flow.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Aarnes, J.E., Efendiev, Y.: An adaptive multiscale method for simulation of fluid flow in heterogeneous porous media. Multiscale Model. Simul. 5(3), 918–939 (2006)

    Article  Google Scholar 

  2. Aarnes, J.E., Krogstad, S., Lie, K.-A.: A hierarchical multiscale method for two-phase flow based upon mixed finite elements and nonuniform coarse grids. Multiscale Model. Simul. 5(2), 337–363 (2006)

    Article  Google Scholar 

  3. Aarnes, J.E., Lie, K.-A., Kippe, V., Krogstad, S.: Multiscale methods for subsurface flow. In: Multiscale modeling and simulation in science, Vol. 66, p 3–48. Springer, Berlin (2009)

  4. Abdulle, A.: On a priori error analysis of fully discrete heterogeneous multiscale FEM. Multiscale Model.Simul. 4(2), 447–459 (2005)

    Article  Google Scholar 

  5. Abdulle, A.: The finite element heterogeneous multiscale method: a computational strategy for multiscale PDEs. In: Multiple scales problems in biomathematics, mechanics, physics and numerics, of GAKUTO International Series Mathematics Science Applications, Vol. 31, pp 133–181 (2009)

  6. Abdulle, A., Engquist, W.E.B., Vanden-Eijnden, E.: The heterogeneous multiscale method. Acta Numer 21, 1–87 (2012)

    Article  Google Scholar 

  7. Abdulle, A., Nonnenmacher, A.: Adaptive finite element heterogeneous multiscale method for homogenization problems. Mech. Engrg Comput. Methods Appl. 200(37-40), 2710–2726 (2011)

    Article  Google Scholar 

  8. Alt, H.W., DiBenedetto, E.: Nonsteady flow of water and oil through inhomogeneous porous media. Ann. Scuola Norm. Sup. Pisa Cl Sci. (4) 12(3), 335–392 (1985)

    Google Scholar 

  9. Allaire, G.: Homogenization, two-scale, convergence. SIAM J. Math. Anal 23(6), 1482–1518 (1992)

    Article  Google Scholar 

  10. Amaziane, B., Antontsev, S., Pankratov, L., Piatnitski, A.: Homogenization of immiscible compressible two-phase flow inporous media: application to gas migration in a nuclear waste repository. Multiscale Model. Simul. 8(5), 2023–2047 (2010)

    Article  Google Scholar 

  11. Arbogast, T.: The existence of weak solutions to single porosity and simple dual-porosity models of two-phase incompressible flow. Nonlinear Anal. 19(11), 1009–1031 (1992)

    Article  Google Scholar 

  12. Antontsev, S., Kazhikhov, A., Monakhov, V.: Boundary value problems in mechanics of nonhomogeneous fluids.Transl. from the Russian. In: Studies in mathematics and its applications 22, p. 309, Amsterdam etc. North- Holland. xii (1990)

  13. Bear, J.: Dynamics of fluids in porous media. American Elsevier, New York (1972)

    Google Scholar 

  14. Bourgeat, A., Hidani, A.: Effective model of two-phase flow in a porous medium made of different rock types. Appl. Anal. 58(1-2), 1–29 (1995)

    Article  Google Scholar 

  15. Bourgeat, A., Luckhaus, S., Mikelić, A.: Convergence of the homogenization process for a double-porosity model of immiscible two-phase flow. SIAM J. Math. Anal. 27(6), 1520–1543 (1996)

    Article  Google Scholar 

  16. Brezzi, F., Franca, L.P., Hughes, T.J.R., Russo, A.: b = ∫ g. Comput. Methods Appl. Mech. Engrg. 145(3-4), 329–339 (1997)

    Article  Google Scholar 

  17. Bush, L., Ginting, V., Presho, M.: Application of a conservative, generalized multiscale finite element method to flow models. J. Comput. Appl. Math. 260, 395–409 (2014)

    Article  Google Scholar 

  18. Cancès, C., Pop, I.S., Vohralík, M.: An a posteriori error estimate for vertex-centered finite volume discretizations of immiscible incompressible two-phase flow. Math. Comp. 83(285), 153–188 (2014)

    Article  Google Scholar 

  19. Chavent, G., Jaffré, J.: Mathematical models and finite elements for reservoir simulation: single phase, multiphase, and multicomponent flows through porous media. Elsevier Science Pub. Co., North-Holland New York (1986)

    Google Scholar 

  20. Chen, Y., Li, Y.: Local-global two-phase upscaling of flow and transport in heterogeneous formations. Multiscale Model.Simul. 8(1), 125–153 (2009)

    Article  Google Scholar 

  21. Chen, Z.: Degenerate two-phase incompressible flow. I. Existence, uniqueness and regularity of a weak solution. J. Diff. Equat. 171(2), 203–232 (2001)

    Article  Google Scholar 

  22. Chen, Z.: Degenerate two-phase incompressible flow. II. Regularity stability and stabilization. J. Differ. Equ. 186(2), 345–376 (2002)

    Article  Google Scholar 

  23. Chen, Z., Ewing, R.E.: Degenerate two-phase incompressible flow. III. Sharp error estimates . Numer. Math. 90(2), 215–240 (2001)

    Article  Google Scholar 

  24. Chen, Z., Hou, T.Y.: A mixed multiscale finite element method for elliptic problems with oscillating coefficients. Math. Comp 72(242), 541–576 (2003)

    Article  Google Scholar 

  25. E, W., Engquist, B.: The heterogeneous multiscale methods. Commun. Math. Sci. 1(1), 87–132 (2003)

    Article  Google Scholar 

  26. Efendiev, Y., Ginting, V., Hou, T., Ewing, R.: Accurate multiscale finite element methods for two-phase flow simulations. J. Comput. Phys. 220(1), 155–174 (2006)

    Article  Google Scholar 

  27. Epshteyn, Y., Rivière, B.: Analysis of hp discontinuous Galerkin methods for incompressible two-phase flow. Comput, J. Appl. Math 225(2), 487–509 (2009)

    Article  Google Scholar 

  28. Eymard, R., Herbin, R., Michel, A.: Mathematical study of a petroleum-engineering scheme. M2AN Math. Model. Numer. Anal. 37(6), 937–972 (2003)

    Article  Google Scholar 

  29. Ginting, V.: Analysis of two-scale finite volume element method for elliptic problem. J. Numer. Math. 12(2), 119–141 (2004)

    Article  Google Scholar 

  30. Gloria, A.: An analytical framework for the numerical homogenization of monotone elliptic operators and quasiconvex energies. Multiscale Model. Simul. 5(3), 996–1043 (2006)

    Article  Google Scholar 

  31. Gloria, A.: An analytical framework for numerical homogenization. II. Windowing and oversampling . Multiscale Model. Simul. 7(1), 274–293 (2008)

    Article  Google Scholar 

  32. Henning, P., Ohlberger, M.: The heterogeneous multiscale finite element method for elliptic homogenization problems in perforated domains. Numer. Math. 113(4), 601–629 (2009)

    Article  Google Scholar 

  33. Henning, P., Ohlberger, M.: Error control and adaptivity for heterogeneous multiscale approximations of nonlinear monotone problems. Discrete Contin. Dyn. Syst. Ser. S 8(1), 119–150 (2015)

    Article  Google Scholar 

  34. Henning, P., Ohlberger, M., Schweizer, B.: Homogenization of the degenerate two-phase flow equations. Math. Models and Methods in Appl. Sciences 23(12), 2323–2352 (2013)

    Article  Google Scholar 

  35. Hou, T.Y., Wu, X.-H.: A multiscale finite element method for elliptic problems in composite materials and porous media. J. Comput. Phys. 134(1), 169–189 (1997)

    Article  Google Scholar 

  36. Huber, R., Helmig, R.: Node-centered finite volume discretizations for the numerical simulation of multiphase flow in heterogeneous porous media. Comput. Geosci. 4(2), 141–164 (2000)

    Article  Google Scholar 

  37. Jenny, P., Lee, S.H., Tchelepi, H.A.: Multi-scale finite-volume method for elliptic problems in subsurface flow simulation. J. Comput. Phys. 187(1), 47–67 (2003)

    Article  Google Scholar 

  38. Jenny, P., Lee, S.H., Tchelepi, H.A.: Adaptive multiscale finite-volume method for multiphase flow and transport in porous media. Multiscale Model. Simul. 3(1), 50–64 (2004)

    Article  Google Scholar 

  39. Jiang, L., Aarnes, J.E., Efendiev, Y.: Some multiscale results using limited global information for two-phase flow simulations. Int. J. Numer. Anal. Model. 9(1), 115–131 (2012)

    Google Scholar 

  40. Jiang, L., Mishev, I.D.: Mixed multiscale finite volume methods for elliptic problems in two-phase flow simulations. Commun. Comput. Phys. 11(1), 19–47 (2012)

    Google Scholar 

  41. Jikov, V.V., Kozlov, S.M., Oleı̆nik, O.A.: Homogenization of differential operators and integral functionals. Springer-Verlag, Berlin (1994). (translated from Russian by G.A. Yosifian)

    Book  Google Scholar 

  42. Chen, Z., Huan, G., Ma., Y.: Computational methods for multiphase flows in porous media. Society for Industrial and Applied Mathematics (SIAM). PA, Philadelphia (2006)

    Book  Google Scholar 

  43. Kröner, D., Luckhaus, S.: Flow of oil and water in a porous medium. J. Differ. Equ. 55(2), 276–288 (1984)

    Article  Google Scholar 

  44. Leverett, M.C., Lewis, W.B.: Steady flow of gas-oil-water mixtures through unconsolidated sands. Trans. of the AIME 142(1), 107–116 (1941)

    Article  Google Scholar 

  45. Lukkassen, D., Nguetseng, G., Wall, P.: Two-scale convergence. Int. J. Pure Appl. Math. 2(1), 35–86 (2002)

    Google Scholar 

  46. Lunati, I., Jenny, P.: Multiscale finite-volume method for density-driven flow in porous media. Comput. Geosci. 12(3), 337–350 (2008)

    Article  Google Scholar 

  47. Lunati, I., Lee, S.H.: An operator formulation of the multiscale finite-volume method with correction function. Multiscale Model. Simul. 8(1), 96–109 (2009)

    Article  Google Scholar 

  48. Målqvist, A., Peterseim, D.: Localization of elliptic multiscale problems. Math. Comp. 83(290), 2583–2603 (2014)

    Article  Google Scholar 

  49. Michel, A.: A finite volume scheme for two-phase immiscible flow in porous media. SIAM J. Numer. Anal. 41(4), 1301–1317 (2003)

    Article  Google Scholar 

  50. Murat, F., Tartar, L.: H-convergence, topics in the mathematical modeling of composite materials. Progr. Nonlinear Differ. Equ. Appl. 31, 21–43 (1997)

    Google Scholar 

  51. Nordbotten, J.M.: Adaptive variational multiscale methods for multiphase flow in porous media. Multiscale Model Simul 7(3), 1455–1473 (2008)

    Article  Google Scholar 

  52. Ohlberger, M.: Convergence of a mixed finite elements–finite volume method for the two phase flow in porous media. East-West J. Numer. Math. 5(3), 183–210 (1997)

    Google Scholar 

  53. Ohlberger, M.: A posteriori error estimates for the heterogeneous multiscale finite element method for elliptic homogenization problems. Multiscale Model. Simul. 4(1), 88–114 (2005)

    Article  Google Scholar 

  54. Owhadi, H., Zhang, L., Berlyand, L.: Polyharmonic homogenization, rough polyharmonic splines and sparse super-localization. M2AN Math. Model. Numer. Anal. 48(2), 517–552 (2014)

    Article  Google Scholar 

  55. Yeh, L.-M.: Homogenization of two-phase flow in fractured media. Math. Models Methods Appl. Sci. 16(10), 1627–1651 (2006)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Numerische und Angewandte Mathematik, Westfälische Wilhelms-Universität Münster, Einsteinstr. 62, D-48149, Münster, Germany

    Patrick Henning & Mario Ohlberger

  2. Fakultät für Mathematik, Technische Universität Dortmund, Vogelpothsweg 87, D-44227, Dortmund, Germany

    Ben Schweizer

Authors
  1. Patrick Henning
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mario Ohlberger
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ben Schweizer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Patrick Henning.

Additional information

This work was supported by the Deutsche Forschungsgemeinschaft under the contract numbers SCHW 639/3-2 and OH 98/4-2.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Henning, P., Ohlberger, M. & Schweizer, B. Adaptive heterogeneous multiscale methods for immiscible two-phase flow in porous media. Comput Geosci 19, 99–114 (2015). https://doi.org/10.1007/s10596-014-9455-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10596-014-9455-6

Keywords

Mathematics Subject Classification (2010)

Search

Navigation