Abstract
The objective of this study is to assess the global impact of sea level rise and to evaluate the effectiveness of adaptation. Global areas of inundation due to sea level rise are identified. The affected populations and the economic damage caused by inundation due to future climate change are estimated for a number of scenarios involving Representative Concentration Pathways (RCP) and Shared Socioeconomic Pathways (SSP). The effects of adaptation in coastal areas, specifically the effects of elevating dikes, are evaluated. According to study results, dikes 1 m in height may reduce the total inundated area by approximately 40% below the no-adaptation baseline under the same RCP. The cost of adaptation was estimated using an original cost database to establish the cost of protection in future socioeconomic scenarios. It was found that the incremental adaptation cost was less than the economic damage in almost all cases of RCP/SSP, providing an incentive to take action to respond to climate change.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Coastal areas—the most densely populated and economically productive areas in the world—are among the primary impact sectors threatened by exposure to climate change. Sea level rise (SLR) will affect tens of millions of people living in low-lying coastal areas, threatening infrastructure, capital assets, ecosystems, and island nations (IPCC 2014). It is virtually certain that global mean SLR will continue beyond 2100 at a rate that will depend on future emissions (Church et al. 2013; Kopp et al. 2016; Bittermann et al. 2017).
Understandably, there has been growing interest in assessing the impact of climate change and the effectiveness of adaptation in these coastal areas. Diaz (2016) defined two categories of coastal impact studies: (1) high-resolution local studies that evaluate the targeted area and adaptation projects and (2) aggregate global exposure surveys that quantify the land, people, and capital at risk of inundation. Many high-resolution local studies have been conducted for site-specific assessments of SLR and adaptation projects but the results of these types of studies cannot be directly extrapolated to global assessment.
Aggregate global exposure surveys are suitable for consistently comparing differences between countries and sectors, and provide a basis for discussing the balance between mitigation and adaptation in international debates. Applying aggregate global exposure survey results to the national scale has been performed for many countriesFootnote 1 but have been examined for the global scale by rather limited communities. In fact, most of these coastal impact assessments for the global scale have been conducted by those applying the Dynamic and Interactive Vulnerability Assessment (DIVA) model, which uses geospatial analysis to divide world coastlines into more than 12 thousand coastal segments. Until the time of the IPCC’s fifth assessment report (IPCC 2014), most impact assessments were based on the Special Report on Emissions Scenarios (SRES; see, for example, Nicholls et al. 2011; Hinkel et al. 2013; Arnell et al. 2016; Brown et al. 2016). In another stream out of the DIVA group, Maruyama and Mimura (2010) estimated the global risk of inundation by combining average SLR projection and a 1/100-year storm surge and assessed the impacts of protection along world coastlines based on SRES.
Studies using new scenarios, so-called Representative Concentration Pathways (RCP) and Shared Socioeconomic Pathways (SSP), have appeared since around 2013; the pioneering work of Hinkel et al. (2014) used the DIVA model based on four General Circulation Models (GCM) and RCP/SSP scenarios and evaluated the impacts of SLR without adaptation as well as the benefits of adaptation. Diaz (2016) used the DIVA database to develop a high-resolution optimization model for least-cost adaptation decisions in response to SLR and storm surge in her Coastal Impact and Adaptation Model (CIAM) based on RCP scenarios. Other studies looking at general equilibrium effects include Bosello et al. (2012) and Pycroft et al. (2016), who distinguished the direct cost and welfare effects on other sectors using a general equilibrium model and also referred to the physical and economic impacts of the DIVA model.
The objective of this study is to assess the global impact of SLR and to evaluate the effectiveness of adaptation based on various RCP/SSP scenarios. First, global areas of inundation and impact due to SLR are identified. Relative SLR includes the local change in the sea surface height relative to land due to factors such as daily and monthly tides (Diaz 2016). The study assesses potential areas of future inundation using the global distribution of dynamic sea level changes of four GCM, including globally averaged ocean thermal expansion and water flux input from land, glaciers, and salinity influences on density. Second, the effects of adaptation in coastal areas, particularly the effects of protection measures, are evaluated. Coastal adaptations to reduce vulnerability are generally classified as protection, accommodation, and retreat (Klein et al. 1999; Hino et al. 2017). Although adaptation has the ability to substantially reduce the negative impacts of SLR (Hinkel et al. 2014), there are few global assessment studies that evaluate the actual impact of adaptation. Economic damage very much depends on the adaptation measures adopted to cope with the consequences of SLR. Our earlier studies (Yotsukuri et al. 2017; Yokoki et al. 2018) evaluated the potential impact of inundation without adaptation. The present study compares the impact of adaptations such as raising the height of dikes with the consequences of no adaptation. In this study, the GCM results did not indicate the catastrophic cases involving more than 1 m mean SLR in 2100 and more than 10 m SLR by 2300 that have been projected by others.Footnote 2 Rather, the effectiveness of protection against gradual and non-catastrophic SLR expected by the end of this century is stressed. Should SLR be significantly higher, it will be necessary to shift to other types of adaptation, including accommodation and retreat, since protection options will not be sufficient to prevent the physical and socioeconomic consequences. Finally, the study analyzes the cost effectiveness of adaptation. The authors have constructed an original cost database for installed coastal protection throughout the world and use the database to estimate the future costs of adaptation. This empirically based approach contrasts with previous studies, which have typically estimated cost by employing theoretical economic models. In this study, the authors’ use their developed cost database and SSP to produce more refined estimates of the costs and benefits of adaptation. Such estimates would seem essential to any discussion of future countermeasures against climate change.
2 Methodology
2.1 Impact assessment of sea level rise and adaptation
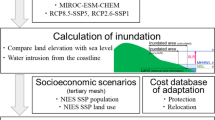
Figure 1 outlines the method. Inundation damage in costal zones is considered to be a significant consequence of SLR. Inundated areas and temporal changes in inundation were estimated using topographic data (ETOPO1; Amante and Eakins 2009), astronomical high tides (that is, mean higher height water level, MHHWL) data, and sea surface height data from four GCM (MIROC-ESM, GFDL-ESM2M, NorESM1-M, and IPSL-CM5A), adjusted vertically at the geoid. ETOPO1, which provides elevation data on land (mean sea level, MSL) and water depth in a 1 arc-minute (about 1.85 km at the equator, varying by latitude) global relief model of the Earth’s surface that integrates land topography and ocean bathymetry, was averaged into 2.5 arc-minute gridded resolution. The elevation map was smoothed to approximately 10 cm resolution to ensure consistency with the land elevation and water depth data of ETOPO1. Global tidal data were obtained from TPXO7.2 (Egbert and Erofeeva 2002). High tides (MHHWL), which occur roughly twice a month, were combined with the four major component tides (M2, K1, S2, and O1). Sea surface height, globally averaged steric sea level, and other outputs of the four GCM were obtained from the NIES database (NIES 2016). The impacts of storm surge were not considered since the study focuses on ordinary inundation impacts rather than the impacts of sudden and local extreme events. Vertical land movement such as subsidence was not accounted for.
Potentially inundated areas without adaptation were identified by comparing sea surface height and land elevation. In the identification process, the areas of the grids of sea water were extended landward if the height of the neighboring landward grid was below the sea surface height. Because there are no accurate and consistent elevation data or maps of installed dikes in coastal areas of the world, this study globally estimated the “potentially inundated area” and the inundated coastline to construct the no-adaptation reference case; for these estimates, existing dikes were not taken into account. Although Kumano et al. (2018) developed a method for generating a world dike distribution map using satellite imaging and a digital surface model, this requires considerably more time to apply on a global scale. Since the SLR projection of MIROC-ESM (Watanabe et al. 2011) is higher than for the other GCM (as noted in Section 3), the study mainly treats the impacts of MIROC-ESM for steric SLR.
By applying the various SSP to the predicted inundated area, the affected population and associated economic damage were estimated. A 0.5-degree grid resolution for the SSP (SSP1-3) was used for population and GDP projections, rescaled by Murakami and Yamagata (2016).Footnote 3 SSP3 (“regional rivalry”) resulted in the largest affected population in 2100, followed in order by SSP2 (“middle of the road”) and SSP1 (“sustainability”) (O’Neill et al. 2017). On the other hand, SSP1 resulted in the largest GDP in 2100, followed by SSP2 and SSP3. The downscaled SSP includes the effects of urban shrinkage/dispersion related to socioeconomic scenarios. However, it does not consider movements due to relocations resulting from gradual inundation, evacuation from urgent inundation, or other variables such as investments in environmental technologies. Projections of the social response to coastal risk are outside the scope of the present study.
The effects of dikes as a protection or adaptation were also evaluated: building dikes to a height of 50 cm and 1 m above the sea surface height along all threatened coastlines. The effectiveness of these measures was estimated by comparing results to a no-adaptation baseline.
2.2 Economic damage
Economic damage and the cost of adaptation persist as important issues in the context of implementing adaptation. In order to estimate in detail the economic damage of inundation using a method comparable to that presented in the flood control and the economic research manual in Japan (MLIT 2005), high-resolution data on land use and the economic value of stocks at the grid level are required. However, such precise and comprehensive data for every part of the world are currently unavailable (Maruyama and Mimura 2010).
In the absence of such data, a macro estimation method was used to approximate the economic impact of inundation. Following the approach of Yotsukuri et al. (2017), economic damage (DC) was empirically estimated by the econometric relationship between past hydrological disasters, the affected population (POPrisk), and GDP per capita (pGDP) using CRED’s EM-DAT database (CRED 2016) and the World Bank’s national statistics.Footnote 4 As shown in Table 1, Yotsukuri et al. (2017) considered two types of econometric estimation: a single damage function for all countries, and three damage functions based on the World Bank’s economic classifications (whereby countries were classified by 2005 real GDP per capita: Low, less than 4125 US$; Middle, 4126–12,735 US$; High, more than 12,736 US$). Estimates of economic damage based on the three-function approach exceeded those based on the single-function method (for single-function results, please see the Supplementary Materials). The three-function approach estimated greater total economic damage since the damage estimates for the three classifications tended to be larger than in the more general single-function case except that the single-function method estimated large economic damage for countries such as China and Vietnam (Yotsukuri et al. 2017). Unless otherwise specified, all monetary values have been converted to 2005 US dollars and not discounted, as in Hinkel et al. (2014).
For purposes of comparison, the study also applied the simplified economic evaluation method of Fankhauser (1995) and the FUND model to our impact assessment for inundation. Following Fankhauser (1995), the FUND model (Darwin and Tol 2001; Anthoff et al. 2010) and DIVA model (see, e.g., Hinkel et al. 2014) estimate economic damages such as wet and dry land losses, which are associated with the per capita income and population density of the affected areas. In these studies, the OECD average of dryland and wetland values were set at 2 and 5 million US$ in 1990 and were assumed to vary as a function of the income density of the land. The detailed procedures are described in the Supplementary Materials.
2.3 Cost of adaptation
To estimate overall cost, it is necessary to specify the design standards and unit cost of adaptation. In this study, a practical or bottom-up approach for estimating the costs of adaptation was used. Scussolini et al. (2016) constructed a global database of flood protection and focused on the flood return period associated with various protection measures. Kumano et al. (2017) examined the design standards of coastal defenses such as sea dikes and constructed a database of the unit costs of projects based on international design standards as recorded in reports such as those of the US Army, the EU, and JICA dealing with technical cooperation projects in developing countries. This database has been updated; 455 cost-of-protection values from 20 countries have been included (please see the Supplementary Materials for the data source). Japanese design guidelines mandate sufficient integrity to withstand a 1/50-year return period of occurrence of tidal levels (MLIT 2007; Miyata et al. 2013).
Future adaptation costs are obtained by multiplying the length of the inundated coastline to be protected and the unit cost of dike construction. The incremental adaptation costs were estimated by assuming two cases—constructing new dikes 1 m in height, and upgrading by 50 cm the height of existing dikes (raising them to a height of 1 m)—along the projected inundated coastline. Unfortunately, no consistent elevation data or maps of currently installed dikes are available. A more realistic adaptation cost could certainly be produced for the two cases if such information was obtainable. The incremental adaptation cost in year t is calculated as in Eqs. (1) and (1′):
where \( \varDelta A{C}_t^N \) and \( \varDelta A{C}_t^U \) are, respectively, the incremental adaptation costs of building new dikes 1 m high and upgrading the height of existing dikes to 1 m in year t [US$]; ΔLj,t is the length of coastline that can be protected with the incremental adaptation in country j in year t [km]; \( U{C}_{j,t}^N \) and \( U{C}_{j,t}^U \) are the unit protection costs in country j in year t [US$/km]; and \( M{C}_{j,t}^N \) and \( M{C}_{j,t}^U \) are the maintenance costs for country j in year t [US$]. Annual maintenance costs depend on the durability (d) of the protection measure (in years): \( M{C}_{j,t}^N=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\left(\varDelta {L}_{j,t}\cdot U{C}_{j,t}^N\right) \) and \( M{C}_{j,t}^N=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\left(\varDelta {L}_{j,t}\cdot U{C}_{j,t}^U\right) \).
The length of the inundated coastline is multiplied by the number and length of the inundated grids according to latitude and longitude. ΔLj,t is determined by comparing the lengths of coastline with and without adaptation, as in Eq. (2):
where \( {L}_{j,t}^0 \) is the length of inundated coastline without adaptation and \( {L}_{j,t}^A \) is the length of inundated coastline with adaptation. This method compares the effects with and without adaptation in the same period but does not assume protection of all the coastline areas that may be inundated in the base period.
Figure 2 plots the unit cost of dike construction. Table A.1 in the Supplementary Materials includes the average and range of the cost, the number of data points, and the construction year. Given that international design standards are similar, the unit cost of protection generally increases with a country’s economic level (i.e., GDP per capita), which is mainly attributable to labor and material costs.Footnote 5 In this study, future unit protection costs were estimated according to each country’s GDP per capita projection of SSP. By regressing construction cost against per capita GDP using data from 20 countries and removing outliers, the unit cost of constructing a new dike 1 m in height can be estimated as \( U{C}_{j,t}^N=892,240 pGD{P}_{j,t}^{0.15611} \). In Japan, the average unit cost of a protective dike is approximately 4.3 million US$/km and normally increases with the height of the dike. Kumano et al. (2017) also estimated a cost of 0.93 million US$/km for a 1 m increase in dike height based on the “model dike” and “the unit price and cost data for civil works” in Japan (Economic Research Association 2016). Accordingly, the unit cost of upgrading dike height by 50 cm was assumed to be \( U{C}_{j,t}^U=190,933 pGD{P}_{j,t}^{0.15611} \) US$/km. However, some diversity exists, even within the same country, depending on the area, land use, and type of construction. There are still limitations that constrain the collection of disclosed cost data for protection and adaptation, although the authors are motivated to collect such data worldwide.
Benefit-cost ratios (B/C) can be calculated as in Eq. (3):
where DC0 is the economic damage without adaptation and DCA is the economic damage with adaptation. Benefit is defined as the difference in economic damage with and without adaptation. Monetary values are not discounted.
3 Results
3.1 Effects of adaptation
Figure 3 shows the world’s inundated areas without adaptation using the four GCM (RCP8.5). MIROC-ESM produced the largest impacts of steric SLR for 2100, followed by NorESM1-M, and GFDL-ESM2M. The regional distribution of high tides (MHHWL), which are about 41 cm on average in MIROC-ESM, was included in the calculations. The remaining analyses were conducted using MIROC-ESM.
Without adaptation but including MHHWL in MIROC-ESM, the inundated areas varied from 370 thousand km2 (RCP2.6) to 420 thousand km2 (RCP8.5) and the affected population varied from 55.3 million (RCP2.6, SSP1) to 106 million (RCP8.5, SSP3).Footnote 6 Countries with the largest inundated areas without adaptation included China, Canada, Vietnam, the USA, Brazil, Australia, Indonesia, and India.Footnote 7 Probabilistic combinations of RCP/SSP were not considered here. Although combinations of RCP8.5 and SSP1 or RCP2.6 and SSP3 may be rare, the study presents the range between the minimum and maximum impacts. Probability analysis will be conducted in subsequent studies. For simplification, the figures show the impact for SSP1 and SSP3; results for SSP2 were between the two.Footnote 8
Next, the effects of adaptation were examined. Figure 4 shows some of the inundated areas with and without 1 m high dikes. Figure 5 compares the inundated areas with and without adaptation. The inundated area total was reduced by approximately 20% for a 50-cm increase in dike height and by 40% in the 1-m case compared to the reference case (no adaptation) under the same RCP. Additionally, in the 1-m case, the affected population in 2100 varied from 42.9 million (RCP2.6, SSP1) to 84 million (RCP8.5, SSP3), reducing the impact by roughly 20–25% under the same RCP/SSP (please see the Supplementary Materials). However, in nearly all cases, the impact of inundation was greater than in the 2020 baseline. Raising the height of dikes alone will not completely eliminate the incremental impact.Footnote 9
Figure 6 shows the economic damage estimates based on the three damage functions. These varied from 169 billion (RCP2.6, SSP3) to 482 billion US$ (RCP8.5, SSP1) in 2100 without any adaptation. With a 1-m dike height, damage varied from 110 billion (RCP2.6, SSP3) to 329 billion US$ (RCP8.5, SSP1). Socioeconomic impacts such as the size of the affected population and the extent of economic damage were more dependent on SSP than RCP. Projected economic damage in 2100 decreased by roughly 30–40% in the 1-m case under the same RCP/SSP scenario, while it decreased by approximately 20% in the 50-cm case.
Figure A.7 in the Supplementary Materials shows economic damage based on the simplified estimation of Fankhauser (1995) and the FUND model, assuming that all potentially inundated areas due to SLR calculated by our impact assessment were counted as “wetland.” Due to its simplicity, this estimation approach may tend to produce the maximum values of economic damage. Damage estimates varied from 743 billion (RCP2.6, SSP3) to 2.052 trillion US$ (RCP8.5, SSP1) in 2100 without adaptation. These results were between our estimation and the much higher results reported by Hinkel et al. (2014), which estimated 180–450 million people flooded and expected losses of 50–80 trillion US$ in 2100 with constant protection (i.e., without incremental adaptation), accounting for the impacts of both SLR and coastal floods. The estimated economic damages using our econometric model can thus be more moderate than the estimates of these other approaches.
3.2 Cost of adaptation
Figure 7 presents the incremental adaptation cost for building new 1 m high dikes or upgrading the height of existing dikes to 1 m. Figure 8 shows the benefit-cost ratios in RCP2.6 and RCP8.5. The range of incremental adaptation costs was estimated both for constructing new dikes 1 m in height and for increasing the height of existing dikes by 50 cm (for a total height of 1 m) along the entire inundated coastline. As noted earlier, given a world dike distribution map, a more realistic adaptation cost could be estimated for these cases. The durability of dikes is assumed to be 30 years. Based on per capita GDP projections, SSP1 involves the highest adaptation cost through 2100, while SSP3 has the lowest cost under the same RCP. Similarly, the adaptation cost under RCP8.5 was the most expensive in the same SSP. Nonetheless, the maximum adaptation cost is still lower than the economic damage in SSP1 and SSP3 under RCP2.6 and RCP8.5 (the RCP4.5 and SSP2 results were between the results for these two scenarios). The results for other combinations are available in the Supplementary Materials.
Using the DIVA database and SRES, UNFCCC (2007) estimated an additional 11–12 billion US$ cost for beach nourishment and dikes to deal with SLR in 2030. Hinkel et al. (2014) estimated expected losses of 50–80 trillion US$ from SLR and coastal floods in 2100 with constant protection, and global costs of 12–71 billion US$ for annual investment and maintenance to protect the coast with dikes. Figure 6 indicated economic damage due to steric SLR without adaptation or flooding was approximately 75–90 billion US$ in 2030 and 169–482 billion US$ in 2100. As in Fig. 7, incremental adaptation cost was less than 20 billion US$ in 2030 and it was 43–203 billion US$ in 2100 under RCP8.5. Incremental adaptation costs were lower than economic damage in almost all RCP/SSP cases.
As shown in Fig. 8, the B/C ratios for upgrading existing dike heights are roughly four times higher than for the case of constructing new dikes. B/C ratios are less than 1 in cases where the entire inundated coastline is fully protected by the construction of new dikes. However, the actual B/C ratios may be larger and between those determined for the extreme cases of either building new dikes only or upgrading existing dikes only. Note that the B/C ratios tend to decrease as time passes and economic damage increases in RCP8.5. The B/C ratios in SSP1 are higher than in SSP3 under the same RCP. The ratios in RCP2.6 are higher than in RCP8.5 under the same SSP. Economic damage increases faster than the effects of adaptation if the adaptation is delayed.
4 Conclusion
This study examined the global impact of steric SLR and evaluated the effectiveness of adaptation measures. The global distribution of projected inundation impacts and temporal changes in SLR-induced inundation were assessed. Among the four GCM considered, MIROC-ESM produced the largest impacts of steric SLR for 2100. In the MIROC-ESM, the size of the inundated areas without adaptation varied from 370 thousand km2 (RCP2.6) to 420 thousand km2 (RCP8.5) in 2100, while the affected population varied from 55.3 million (RCP2.6, SSP1) to 106 million (RCP8.5, SSP3). Socioeconomic impacts such as the size of the affected population and economic damage were more dependent on SSP than RCP.
The effects of adaptation in coastal areas were also examined, specifically the effects of elevating dikes. Increasing the height of dikes by 50 cm reduced the total inundated area by approximately 20% from the case without adaptation, while a 1-m increase in dike height resulted in a 40% reduction under the same RCP. In the 1-m case, the affected population in 2100 varied from 42.9 million (RCP2.6, SSP1) to 84 million (RCP8.5, SSP3), reducing the impact by roughly 20–25% under the same RCP/SSP.
Economic damage and the cost of adaptation were compared by using a cost database and various future scenarios. It was found that incremental adaptation costs were lower than the economic damage in all cases under the same RCP scenario. Because there are still limitations that constrain the collection of disclosed cost data and a comprehensive geological distribution for protection and adaptation, the adaptation scenarios were restricted to either (1) constructing new 1 m high dikes or (2) upgrading existing dikes by increasing their height by 50 cm (to 1 m) along all of the inundated coastline. With access to additional data, it should be possible to determine more realistic costs between these extremes. Other adaptations such as beach nourishment and planting mangroves can be similarly evaluated given a proper cost database and specific protection standards.
A number of issues and uncertainties need to be addressed further. Catastrophic sea level changes due to changes in the mass of the ocean from melting glaciers or ice sheets were not included here. Tackling the uncertainties of projecting social response to climate risk, associated with SSP downscaling and proactive rather than reactive adaptation, is also left as future work.
Despite these acknowledged uncertainties and limitations, a framework for assessing the impact of inundation due to SLR, the effectiveness of adaptation, and the cost of adaptation measures was established. This study demonstrates how adaptation can reduce inundation impacts in coastal areas and that incremental adaptation costs may be much lower than economic damage without adaptation. Such results provide a powerful incentive to take action to lessen the effects of climate change.
Notes
Although Jones and O’Neill (2016) recently applied a 0.125-degree SSP, this study used a 0.5-degree projection in light of data availability and verifiability. Higher resolution experiments will be a future task.
Yanai et al. (2017) examined and compared these two methods for estimating economic damage in Japan, applying them to the historical case of the Isewan Typhoon in 1959. The comparison showed that the former gave estimates of economic damage that were 10 times larger than what was reported by local municipalities, while the latter gave estimates that were lower than what was reported.
Jonkman et al. (2013) suggested that the total cost might be dependent on material and labor costs and that it might increase almost linearly according to the height of the dikes, based on an analysis of the cost of sea dikes in the Netherlands, USA, and Vietnam.
Although the regional distribution of steric SLR differs in the four GCM, the order of the 10 major countries with the largest inundated areas without adaptation was nearly the same.
The results of other combinations are available upon request.
References
Amante C, Eakins BW (2009) ETOPO1: 1 arc-minute global relief model: procedures, data sources and analysis. NOAA Technical Memorandum NESDIS NGDC-24, 19p
Anthoff D, Nicholls RJ, Tol RSJ (2010) The economic impact of substantial sea-level rise. Mitig Adapt Strateg Glob Chang 15(4):321–335
Arnell NW, Brown S, Gosling SN, Hinkel J, Huntingford C, Lloyd-Hughes B, Lowe JA, Osborn T, Nicholls RJ, Zelazowski P (2016) Global-scale climate impact functions: the relationship between climate forcing and impact. Clim Chang 134(3):475–487
Bittermann K, Rahmstorf S, Kopp RE, Kemp AC (2017) Global mean sea-level rise in a world agreed upon in Paris. Environ Res Lett 12:124010
Bosello F, Nicholls RJ, Richards J, Roson R, Tol RSJ (2012) Economic impacts of climate change in Europe: sea-level rise. Clim Chang 112(1):63–81
Brown S, Nicholls RJ, Lowe JA, Hinkel J (2016) Spatial variations of sea-level rise and impacts: an application of DIVA. Clim Chang 134(3):403–416
Church JA et al (2013) Sea level change. Climate change. In: Stocker TF et al (eds) The physical science basis. Contribution of working group I to the fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, p 2013
CRED (2016) EM-DAT: the international disaster database, http://www.emdat.be/
Darwin RF, Tol RSJ (2001) Estimates of the economic effects of sea level rise. Environ Resour Econ 19(2):113–129
DeConto RM, Pollard D (2016) Contribution of Antarctica to past and future sea-level rise. Nature 531(7596):591–597
Diaz DB (2016) Estimating global damages from sea level rise with the Coastal Impact and Adaptation Model (CIAM). Clim Chang 137(1):143–156
Economic Research Association (2016) Unit price and cost data for civil works. Economic Research Association (in Japanese)
Egbert GD, Erofeeva SY (2002) Efficient inverse modeling of Barotropic ocean tides. J Atmos Ocean Technol 19(2):183–204
Fankhauser S (1995) Protection vs. retreat: the economic costs of sea level rise. Environ Plan A 27(2):299–319
Hauer ME, Evans JM, Mishra DR (2016) Millions projected to be at risk from sea-level rise in the continental United States. Nat Clim Chang 6(3):691–695
Hinkel J, van Vuuren DP, Nicholls RJ, Klein RJT (2013) The effects of mitigation and adaptation on coastal impacts in the 21st century. Clim Chang 117(17):783–794
Hinkel J, Lincke D, Vafeidis AT, Perrette M, Nicholls RJ, Tol RSJ, Marzeion B, Fettweis X, Ionescu C, Levermann A (2014) Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc Natl Acad Sci 111(9):3292–3297
Hino M, Field CB, Mach KJ (2017) Managed retreat as a response to natural hazard risk. Nat Clim Chang 7(5):364–370
IPCC (2014) Climate change 2014: impacts, adaptation and vulnerability. Contribution of working group II to the fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge
Jones B, O’Neill BC (2016) Spatially explicit global population scenarios consistent with the Shared Socioeconomic Pathways. Environ Res Lett 11(8):084003 10p
Jonkman SN, Hillen MM, Nicholls RJ, Kanning W, van Ledden M (2013) Costs of adapting coastal defences to sea-level rise: new estimates and their implications. J Coast Res 29(5):1212–1226
Klein RJT, Nicholls RJ, Mimura N (1999) Coastal adaptation to climate change: can the IPCC technical guidelines by applied? Mitig Adapt Strateg Glob Chang 4(3):51–64
Kopp RE, Kemp AC, Bitterman K, Horton BP, Donnelly JP, Gehrels WR, Hay CC, Mitrovica JX, Morrow ED, Rahmstorf S (2016) Temperature-driven global sea-level variability in the Common Era. Proc Natl Acad Sci 113(11):E1434–E1441
Kopp RE, DeConto RM, Bader DA, Hay CC, Horton RM, Kulp S, Oppenheimer M, Pollard D, Strauss BH (2017) Evolving understanding of Antarctic ice-sheet physics and ambiguity in probabilistic sea-level projections. Earth’s Future 5:1217–1233
Kumano N, Tuchida K, Tamura M, Kuwahara Y, Yokoki H (2017) Estimating the cost of coastal protection based on socioeconomic scenarios in Japan. Journal of Japan Society of Civil Engineers B3 (Ocean Engineering) 73(2): I_1007-I_1012 (in Japanese)
Kumano N, Kawashima R, Yanai H, Tamura M, Yokoki H, Kuwahara Y (2018) Generation of world dyke distribution map using satellite image and digital surface model. J Coast Zone Stud 30(4):89–100 (in Japanese)
Maruyama Y, Mimura N (2010) Global assessment of climate change impacts on coastal zones with combined effects of population and economic growth. Environ Syst Res 38:255–263 (in Japanese)
MLIT (Ministry of Land, Infrastructure and Transport) (2005) The flood control and the economic research manual (in Japanese)
MLIT (Ministry of Land, Infrastructure and Transport) (2007) Technical standards and commentaries for port and harbour facilities in Japan. The Ports and Harbours Association of Japan (in Japanese)
Miyata M, Nakano T, Harada T, Yamamoto K, Asai S (2013) A study on internationalization of technical standards for port and harbour facilities of Japan: example study on effort to assist in developing port design standards in Vietnam. Technical Note of National Institute for Land and Infrastructure Management, No. 769, 181p
Murakami D, Yamagata Y (2016) Estimation of gridded population and GDP scenarios with spatially explicit statistical downscaling. ArXiv 1610:09041
Nicholls RJ, Marinova N, Lowe JA, Brown S, Vellinga P, de Gusmão D, Hinkel J, Tol RSJ (2011) Sea-level rise and its possible impacts given a ‘beyond 4°C world’ in the twenty-first century. Phil Trans R Soc A 369(1934):161–181
NIES (National Institute for Environmental Studies) (2016) Global meteorological data server, http://h08.nies.go.jp/ddc/
O’Neill BC, Kriegler E, Ebi KL, Kemp-Benedict E, Riahi K, Rothman DS, van Ruijven BJ, van Vuuren DP, Birkmann J (2017) The roads ahead: narratives for shared socioeconomic pathways describing world futures in the 21st century. Glob Environ Chang 42:169–180
Pycroft J, Abrell J, Ciscar J-C (2016) The global impacts of extreme sea-level rise: a comprehensive economic assessment. Environ Resour Econ 64(2):222–253
Scussolini P, Aerts JCJH, Jongman B, Bouwer LM, Winsemius HC, de Moel H, Ward PJ (2016) An evolving global database of flood protection standards. Nat Hazards Earth Syst Sci 16(5):1049–1061
Suzuki T (2014) Prediction of storm surge damage based on climate change estimation with GHG representative concentration pathways. Japan Society of Civil Engineers B2 (Coastal Engineering) 70(2): I_1194-I_1199 (in Japanese)
UNFCCC (2007) Investment and financial flows to address climate change: background paper on the analysis of existing and planned investment and financial flows relevant to the development of effective and appropriate international response to climate change. United Nations Framework Convention on Climate Change, UNFCCC Secretariat, Bonn, Germany, 272p
Watanabe S, Hajima T, Sudo K, Nagashima T, Takemura T, Okajima H, Nozawa T, Kawase H, Abe M, Yokohata T, Ise T, Sato H, Kato E, Takata K, Emori S, Kawamiya M (2011) MIROC-ESM 2010: model description and basic results of CMIP5-20c3m experiments. Geosci Model Dev 4(4):845–872
Yanai H, Kumano N, Tamura M, Yokoki H, Kuwahara Y (2017) Verification of the estimation method for economic damage of storm surge in the case of Isewan typhoon. Journal of Japan Society of Civil Engineers G (Environment) 73(5): I_361-I_367 (in Japanese)
Yokoki H, Tamura M, Yotsukuri M, Kumano N, Kuwahara Y (2018) Global distribution of projected dynamic ocean sea level changes using multiple climate models and economic assessment of sea level rise. CLIVAR Exchanges 74:36–39
Yotsukuri M, Tamura M, Kumano N, Masunaga E, Yokoki H (2017) Global impact assessment of sea level rise based on RCP/SSP scenarios. Journal of Japan Society of Civil Engineers G (Environment) 73(5): I_369-I_376 (in Japanese)
Acknowledgements
We appreciate the support of Mr. Koujiro Tsuchida in Ibaraki University.
Funding
This study was supported by the Environment Research and Technology Development Fund (S-14 and 2-1712) of the Ministry of the Environment and a Grant-in-Aid for Scientific Research (B: 26281055) from MEXT, Japan.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
ESM 1
(DOC 936 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tamura, M., Kumano, N., Yotsukuri, M. et al. Global assessment of the effectiveness of adaptation in coastal areas based on RCP/SSP scenarios. Climatic Change 152, 363–377 (2019). https://doi.org/10.1007/s10584-018-2356-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-018-2356-2