Abstract
Highly populated, water-limited and warm drylands are challenging areas for development and are expected to expand overall under several scenarios of climate change. Here, we adopt a bioclimatic approach based on the Köppen classification to focus on the evolution of warm semi-arid regions over the projected twenty-first century, following three socio-economic scenarios and 12 global climate models from the last IPCC exercise (CMIP5). We show that a global expansion of this climatic domain has already started according to climate observations in the twentieth century (about + 13% of surface increase, i.e. from 6 to 7% of the global land surface). Models project that this expansion will continue throughout the twenty-first century, whatever the scenario: for the most dramatic one (RCP 8.5), the share of the total land surface occupied by warm semi-arid surfaces is about 38% higher in 2100 compared to the present (from ∼ 7 to ∼ 9% of the global land surface). This expansion will essentially take place outside of the tropical belt, showing a poleward migration as large as 11∘ of latitude in the Northern Hemisphere. This expansion is linearly correlated with the projected future global warming (about 853 millions km2 per degree of warming for RCP 8.5). Different types of climate class transitions and their associated mechanisms are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Two billion people (34% of the population) today live in the so-called drylands, which cover about 41% of the terrestrial land surface, according to the United Nations Convention to Combat Desertification (Yukie and Otto 2011). These water-limited areas hold scarce natural resources and thus represent challenging regions for human societies who tend to show weaker wealth and health scores compared to the world population (Reynolds et al. 2007). The future of those drylands is thus preoccupying for populations already submitted to difficult conditions: the degradation of eco-climatic conditions could lead to a reduction of limited natural resources, bringing the socio-ecosystem closer to an equilibrium breaking point. Moreover, the expansion of similar regions could draw more populations into dealing with aridity issues that they have not been accustomed to. In this paper, we focus on a specific sub-domain of the global drylands: semi-arid (SA) regions. More specifically, because even beyond aridity, warm and cold regions hold different challenges (to be reflected in coping strategies, such as, e.g. tropical agroforestry), we focus on warm semi-arid regions (WSAR). As the overall drylands’ area is expected to widen under several scenarios of climatic change (e.g. Feng and Fu (2013)), are existing WSAR expected to aridify? In that case, currently adequate development actions could become obsolete. On the other hand, should we expect the total WSAR area to increase in the future? This could enlarge the geographical relevance of aridity coping strategies. Our goal here is to quantify the total WSA area over the twentieth and the twenty-first century using the most up-to-date climate data and projections and to characterize the geographical extension, distribution and transformation of these regions.
Two main approaches are found in the literature to study the evolution of climatic regions and of drylands specifically. A purely climatic definition uses the precipitation (P) over potential evapotranspiration (PET) ratio (aridity index). Different levels of aridity are distinguished based on consensual thresholds (Yukie and Otto 2011): 0.65 (sub-humid), 0.5 (semi-arid), 0.2 (full arid) and 0.05 (hyper-arid). An alternative definition is based on the application of one of the several existing climate classifications, among which the Köppen one is the most widely used (Rubel and Kottek 2010). In this classification, temperature (T) and precipitation (P) are the variables used to delimitate climate classes separated by empirical thresholds: these are based on expert knowledge of the climatic conditions of existence of generic biomes. This method has been applied to study climatic shifts at the planet scale (e.g. Fraedrich et al. (2001) for the twentieth century; Rubel and Kottek (2010) for the twenty-first century). While the aridity index approach quantifies atmospheric dryness, the climate classification approach is biome-based, allowing common treatment of areas of similar climatic and ecological conditions. Whatever the chosen approach, the evolution of the climatic regions in the future is usually studied through the same overall methodological framework: the definition is applied to time series of climatic data obtained from observations or model simulations, thus producing time series of the localization and the surface extent of the considered climatic regions (e.g. Feng and Fu (2013) for the aridity index; Rubel and Kottek (2010) for the bioclimatic definition). Although both definitions would allow to study the geographical evolution of drylands, the aridity index only classifies levels of aridity whereas the bioclimatic approach further offers the possibility to analyze all types of climatic conversions between classes. WSA conditions constitute a specific class in the Köppen classification. Besides, this classification has been proved a suitable tool for broad-audience climate science communication (Jylhä et al. 2010). For these reasons, the bioclimatic approach was chosen to perform the present study. Section 2 presents the data sets and methods along with introducing an original index of the WSAR geographical extent. The following questions are then addressed:
-
Has the total domain covered by WSAR increased during the twentieth century? (Section 3)
-
Is such an increase expected for the projected twenty-first century? (Section 4)
-
Is the time evolution of WSAR correlated to global warming? (Section 4)
-
Where are those changes located and what are the climatic transitions involved? (Section 4)
The validity of the results is discussed in Section 5.
2 Material and methods
2.1 The climate classification
Köppen (1900) had chosen to classify climate based on the distribution of biomes such as forests, savanas, steppes and deserts. The climate classes are then based on the relationship between climate and vegetation, following increasing levels of complexity. Five main climatic groups are first defined, labeled from A (equatorial climates) to E (polar climates). Groups B, C and D respectively stand for “arid”, “warm temperate” and ‘snow” climates. Each group is further divided into sub-classes, using empirical temperature and precipitation thresholds (cf. full nomenclature in Table Supplementary Materials 1). The classification is based on monthly mean air temperature and cumulated precipitation only. The various formula and criteria can be found in Kottek et al. (2006). All groups but B are first discriminated by temperature criteria. Further subdivisions for groups A, C and D are then calculated based on precipitation criteria. WSA climatic conditions belong to group B of arid climates. This group is characterized at the first order by a dryness threshold (Pth in mm), calculated as a linear function of Tann, the absolute measure of the annual mean temperature in degrees celsius, parameterized accordingly to the annual distribution of precipitation over two semesters (Kottek et al. (2006), formula 2.1):
if at least 2/3 of the annual precipitation occurs in winter,
if at least 2/3 of the annual precipitation occurs in summer,
otherwise.
Precipitation thus identifies arid climate classes, although temperature influences precipitation critical thresholds. The arid climate group is further subdivided first into two sub-classes, based on annual mean precipitation (Pann): steppes (5*Pth < Pann < 10*Pth) are differentiated from deserts (Pann < 5*Pth); then, these are split between warm (Tann > 18∘C) and cold. In the following, we define WSAR to be locations where the Köppen classification identifies warm steppe. The rationale behind this T-dependence of Pth relies on the influence of T on potential evapotranspiration (PET): warming induces PET to rise, thus increasing the level of P needed to pass the threshold of aridity. This particular feature will be further discussed in Section 5, but already implies that, in a warmer world, without any change in Pann, more regions will be considered as WSA as all values (thresholds) depending on Pth will be raised (larger).
2.2 The climate data sets
CRU data set for present-day conditions
Observational data is used to characterize the state and trends of WSAR over the twentieth century. Data from the Climatic Research Unit (CRU) of the University of East Anglia (Mitchell and Jones 2005) is chosen as our reference climatic data set, as is often done in the literature (e.g. Rubel and Kottek (2010)). Monthly temperature and precipitation, for all years from 1901 to 2001, were selected for this purpose. The data set is provided at the horizontal resolution of 0.5∘ latitude by 0.5∘ longitude.
CMIP5 outputs for future projections
To address future climate projected changes, we have retrieved globally gridded monthly precipitation and air temperature from the Coupled Model Intercomparison Project (CMIP5) long-term experiments, for 12 models out of about 30 available (Table Supplementary Materials 2). Only those where several runs (ensemble of simulations for one model and one scenario) are available for at least one of the time-series (historical or future) were selected: all ensemble members are then averaged together for each model, so as to account for the models’ internal variability and provide an unbiased estimate of the forced climate response in individual model simulations (Taylor et al. 2012; Kravtsov et al. 2015). For each model, the 1901–2005 period is extracted from the model ensemble mean historical experiment (forced by observed atmospheric composition changes). For the future, the 2006–2100 period has been selected for three representative concentration pathways (RCPs). RCP 2.6 stands as the “mitigation scenario”: the radiative forcing is projected to peak toward the middle of the twenty-first century, then declines (Riahi et al. 2007); RCP 4.5 is a “stabilization scenario”: the radiative forcing stabilizes by 2100 (Fujino et al. 2006; Hijioka et al. 2008); RCP 8.5 is a “business as usual scenario”: the radiative forcing rises continuously across the twenty-first century, without peaking (Van Vuuren et al. 2011). All future scenarios were forced using prescribed atmospheric composition changes.
2.3 The methodology
Time-series of running averages
In order to buffer year-to-year variability, the climate classification is computed for 15-year-mean climatologies—the optimal averaging windows for climate classifications according to Fraedrich et al. (2001). The total area (global or regional) can then be calculated for a given climate class (e.g. “warm semi-arid”) for each 15-year period. The time-series of such 15-year running area then allow searching for trends. The last 15-year-average of the RCP time series (2086–2100) is used to characterize the climate state at the end of each RCP. The average 1987–2001 period of the historical time-series is used to characterize the climate state at the end of the twentieth century. These analyses are performed at each model’s resolution.
Multi-model mean classification
In order to provide ensemble mean results, average temperature and precipitation time series are calculated for each RCP (over the 1901–2100 period) as the arithmetic mean of all the models (each model resulting from the mean of the runs, as stated in Section 2.2). Based on this mean climatology, the ensemble mean Köppen classification is calculated following the same path as for any of the models. This approach will allow for multi-model ensemble mean maps to be produced. In order to calculate multi-model mean (MMM) averages, the time-series are first projected onto a common grid by linear interpolation. An intermediate grid (1.4∘×1.4∘) is arbitrarily chosen amongst the models’ grids. Such post-treatment partly deteriorates each model’s original outputs. However, the MMM has been shown to give the overall best simulation results compared to observations, although some models perform better for given regions and variables (Gleckler et al. 2008).
WSA domain outer limits
The northern and southern latitudinal boundaries of the overall WSA domain are calculated respectively as the polarmost latitudes enclosing 75% of the total hemispheric WSA surface.
T and P effect
A complementary analysis is provided in the supplementary material to separate T and P effects on WSA changes (see section Supplementary Materials 5).
3 Twentieth century distribution and evolution of warm semi-arid regions
3.1 Results obtained from climate observations
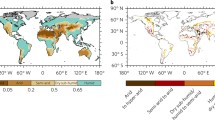
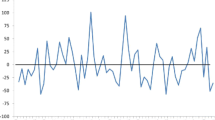
As of today (1987–2001, 15-year period), the WSA total area represents about 7% of the global land surface, according to our calculations of Köppen’s bioclimatic class based on the CRU data set (Fig. 1). Seventy-one percent of those regions is enclosed within the tropical belt. The main warm semi-arid regions (WSAR) are found in the Sahelian belt, the Horn of Africa, central southern Africa, large parts of Australia and, to a lesser extent, in western India and Pakistan, in the eastern foothill of the Andes cordillera, northeastern Brazil, parts of northern Mexico and in the Mediterranean basin. Despite a rather large decadal variability (Fig. 2, black curve), WSAR display a clear increasing trend during the second half of the century (smoothed red curve). By the end of the century, WSAR have increased by + 13% compared to the years 1901–1915 (from 6 to 7% of the total land surface). This change can be seen on Fig. 1 when comparing the red and the black curves. The surface increase occurred primarily across the Tropic of Capricorn in the Southern Hemisphere, and also to some extent in the Sahelian belt in the Northern Hemisphere. Huang et al. (2016) and Feng and Fu (2013) also analysed global semi-arid (SA) climate changes focusing on the twentieth century. From observations, both studies found that WSA have been expanding over the last 60 years, consistently with the present results. However, as they do not differentiate between cold and warm SA regions, their results cannot be directly and quantitatively compared to ours. P is found to be the main driver of this change (Table Supplementary Materials 3): it explains about 75% of the change, while T only explains 23%.
World Köppen climate classification for the averaged 1987–2001 climatology using the CRU data. On the right, zonal sum of WSA surface for the same time period (red) and for the 1901–1915 period (black). The full names of the climate classes are given in Table Supplementary Materials 2
3.2 Results obtained with model simulations
The Köppen classification for the 1987–2001 period and for all selected climate models (cf. Fig. Supplementary Materials 1) are to be compared to the corresponding one drawn for observational data (Fig. 1). Overall, the main WSA regions (the Sahelian belt, the southern African region, northern India, North America and Oceania) are captured by all models, although they show differences in the precise localization of these regions and in their surface extent (it is particularly clear for the Sahelian belt). The case of the Mediterranean basin, South America and central India, identified with the CRU data, is less consensual: some of the models do not identify them as WSAR (e.g. the Mediterranean basin in the IPSL-CM5A-LR model). Large parts of Central America are identified as WSA in some of the models, whereas they are not with the CRU data.
As for what we think is an important feature of past evolution—the increasing trend of the total WSA area observed with the CRU data—only about half of the models display a comparable trend (Fig. Supplementary Materials 2), although with a smaller rate of increase and differing timing. The remaining half shows interannual variability and often decadal or multi-decadal variability but with no obvious trend. Besides, the main driver of WSA changes is T at ∼ 54% (MMM average, Table Supplementary Materials 4), contrary to the result for the CRU data (Section 3.1). This relative failure of climate models to reproduce past trends in the expansion of dry regions has been found in prior research (e.g. Johanson and Fu 2009). This implies that projected future changes need to be interpreted carefully, especially if they are to be used by, e.g. socio-economic actors in those regions. However, we believe there is some value in addressing how those WSAR will change in the future, using climate models, as we will target the mechanisms of change in WSAR and the robustness of responses amongst models.
4 Projected evolution of WSAR for the twenty-first century
In this section, consistency between the model projections will be assumed as robustness, i.e. as some confidence that such changes are more likely to happen than others.
4.1 A global increasing trend
For all three scenarios and all models, the total Earth’s WSA area shows an increasing trend over the first half of the twenty-first century. Figure 3 illustrates the evolution of the multi-model mean (thick line) together with the dispersion amongst the models’ responses. The trend is visible for all separated models of the ensemble (Fig. Supplementary Materials 3). The MMM net increase between the start and end of the twenty-first century, for all three RCPs reaches + 14, + 19 and + 38% for, respectively, RCPs 2.6, 4.5 and 8.5 (Table 1a). It corresponds to rises from ∼ 7.0% of the total land surface in 1987–2001 to, respectively, ∼ 7.6, ∼ 7.9 and ∼ 9.1% in 2086–2100. However, the increasing trend is not continuous over the whole twenty-first century for all RCPs. It is pronounced throughout the twenty-first century for RCP 8.5 (in red, Fig. 3), but levels off before the end of the twenty-first century for the other two RCPs (in blue and in green). Indeed, Table 1a shows that the end-of-twenty-first-century WSA surface increase for RCP 2.6 is already reached by the middle of the twenty-first century (2050–2065). No further increase occurs during the second half of this century. On the contrary, both RCPs 4.5 and 8.5 show a continuing increase after the middle of the twenty-first century, but it is more pronounced for RCP 8.5. These patterns of projected changes were expectable, as they follow the scenarios’ design for CO2 emissions: the radiative forcing is projected to peak by the middle of the century for RCP 2.6 and to go on rising after 2100 for RCP 8.5 (Van Vuuren et al. 2011).
GlobalWSA surface evolution over the twentieth and the twenty-first centuries according to CMIP5 multi-model ensemble. Surfaces are expressed in 103 km2. Bold lines represent the multi-model means. Colored spread represent the multi-model dispersion (quartiles 1 and 3). The historical period, RCPs 2.6, 4.5 and 8.5 are in black, blue, green and red, respectively
4.2 Linear correlation with global warming
This total WSA surface increase shows an almost linear relationship with the net annual global warming as displayed in Fig. 4 (top). At the global scale, a 1∘C increase in temperature during the twenty-first century induces an increase of about 853 ×103 km2 (with an R-square of 0.424). Within the tropical belt, the WSA area increase is of a lesser magnitude than in the extra-tropics (Fig. 4, bottom), and it shows a relatively small increase per degree of warming, while the correlation for the extra-tropical region (summing the WSA for both hemispheres) is quite larger than that obtained for the whole planet, with a higher R-square (equal to 0.61). To our knowledge, this linear correlation has never been explicitly shown before.
Net Global (top), tropical (bottom-left) and extra-topical (bottom-right) WSA Surface increase relatively to the temperature increase between the beginning and the end of the twenty-first century according to the CMIP5 multi-model ensemble. The 12 models are represented by a dot each, for each scenario in color
4.3 Large changes in the sub-tropics
This greater increase of WSAR outside the tropical belt, especially for RCP 8.5, characterizes the poleward expansion of WSAR in both hemispheres. The extra-tropics total WSA surface increased by 80% at the end of the twenty-first century (with respect to the end of the twentieth century) for RCP 8.5, 46 and 27% for RCPs 4.5 and 2.6, respectively. Within the tropics the increase is respectively 23, 9 and 6% (Table 1b–c). This leads to the migration, in the Northern Hemisphere, of the latitude encompassing 75% of the WSA surface between the equator and the pole by + 1∘ N (for the multi-model mean), + 4∘ N and + 11∘ N, respectively, for RCPs 2.6, 4.5 and 8.5 by the end of the twenty-first century (Fig. 5). The poleward migration is of smaller amplitude (lower than 1∘ S) in the Southern Hemisphere (Fig. Supplementary Materials 4). This may be due to the higher spread between the models in quantifying the WSA total area in the Southern compared to the Northern Hemisphere (Fig. Supplementary Materials 5).
Time evolution of the polarmost limit enclosing 75% of the WSA area in the northern hemisphere according to the CMIP5 multi-model ensemble. Degrees of latitudes are on the y-axis. The multi-model variability (quartiles 1 and 3) is represented by the color spread. Segments on the right represent the multi-model spread for the average 2086–2100 period. RCPs 2.6, 4.5 and 8.5 are respectively drawn in blue, green and red
4.4 Mechanisms of change
Four main climate class-transitions to and from the WSA class occur. The total area involved in each type is quantified for both directions (Fig. 6a). Except for the WSA/cold SA transition occurring at the same aridity level, all other transitions lean towards the most arid class: the “fully arid” class gains areas transitioning from the WSA domain, whilst the latter increases of new areas gained from the “equatorial subhumid” and the “warm temperate” classes. The evolution of the WSAR therefore derives from an overall aridification process. Changes are more profound for more severe scenarios: according to RCP 8.5, 58% (for the MMM) of the present WSAR will remain WSA in the future (2100), while 21% (corresponding to 2818 ×103 km2) of the initial area will evolve towards the “fully arid” class. More stability is obtained for RCPs 2.6 and 4.5: respectively 75 and 69% of WSAR are maintained while 8 and 13% become more arid. On the other hand, up to 12 and 19% (for the MMM) of the future WSAR total area will be inherited from “equatorial” and “warm temperate” climate classes, respectively, for the most severe scenario.
Moreover, the complementary analysis (section Supplementary Materials 5) shows that T is the main driver of the global WSA surface change between the beginning and the end of the twenty-first century: for RCP 8.5, T and P account respectively for ∼ 69 and ∼ 17% of this change (Table Supplementary Materials 5). While the T effect leads to conversions to arider climate classes, the P effect induces either wetting or drying impacts according to the region (Fig. Supplementary Materials 6). At the global scale, the global net increase of the WSA area is thus almost entirely due to T, whereas the sign of changes (expansion or contraction) due to P alone is inconclusive (Table Supplementary Materials 6).
Regionally, these different types of conversion are heterogeneously distributed over the globe (Fig. 6b for the MMM results), and specific mechanisms may be identified from the related literature. Under tropical latitudes, new WSA regions are mostly converted from equatorial sub-humid climates, particularly in Central America and northeastern Brazil. This is in line with the projected reduced precipitation in most models as discussed by Christensen et al. (2013), in response to changes in atmospheric circulation in this area (e.g. strengthening of the Caribbean low-level jet, increased subsidence). As for the future new extra-tropical WSA surfaces, they result from the warming of the cold semi-arid class, or the conversion of temperate classes. The increase in WSAR we found in the Mediterranean region is consistent with the increased subsidence and sea-level pressure described by Lu et al. (2007) in response to global warming. In Australia, the global weakening of the Walker circulation, combined with warming, is the potential candidate for our simulated changes (Power and Kociuba 2011). WSAR becoming “sub-humid” are mainly located in East Africa (Fig. Supplementary Materials 7), consistently with the projected precipitation increase in this region (Collins et al. 2013).
5 Discussion
This work fits within a corpus of studies anticipating the evolution of the different climatic regions of the world, albeit with a particular focus on drylands and SA regions. These use a range of definitions and identification tools for these climatic regions, that makes their intercomparison difficult. For example, drylands (Feng et al. 2014), semi-arid—cold and warm—areas (Feng and Fu 2013) do not admit exactly the same boundaries when calculated using the aridity index—and its range of PET algorithms—(Feng and Fu 2013) or one classification amongst Thornthwaite (Feddema 2005), Köppen-Geiger (Rubel and Kottek 2010), Köppen-Trewartha (Feng et al. 2014).
5.1 How do past changes compare with existing literature?
Fraedrich et al. (2001), using the Köppen classification, do not focus specifically on WSA regions. Nevertheless, for the twentieth century, they show that climate shifts (black dots on their Fig. 1) occurred at the geographical frontiers between climate regions, particularly so around WSA areas. Fraedrich et al. (2001) show that the evolution of different climate groups, in terms of extent, is correlated to the evolution of indices of the global atmospheric circulation for the twentieth century. They diagnose an expansion of the tropical belt manifested by the increase in equatorial climates’ surfaces.
Our results for the CRU data show that 75% of the WSA surface changes between the begining and the end of the twentieth century are due to precipitation, while only 23% are due to global warming over this period (Table Supplementary Materials 3). Moreover, WSA areas showed a poleward migration in both hemispheres during the second half of the twentieth century, for CRU data (Fig. Supplementary Materials 8). These results are consistent with observations of the widening of the Hadley circulation (HC) (Seidel et al. 2008; Johanson and Fu 2009). The subtropical dry subsidence zones associated with the poleward branch of the HC indeed correspond to arid/SA climates, hence defining the tropical edges of the SA regions. On the other hand, the results found for the same period but with the models’ data show that T is the main driver of WSA changes (Table Supplementary Materials 4). This is consistent with a defective representation of the precipitations in the models reported in the literature (Ji et al. 2015).
5.2 What about the future expansion of drylands?
As for the twenty-first century, Rubel and Kottek (2010) find, for two future climate scenarios, that the majority of conversions from one class to another is towards drying. Our work here expands on these conclusions by quantifying the area and pointing to the location of lost, stable and appearing WSAR. Moreover, they confirm our findings that the most visible climate changes may be found in the Northern Hemisphere (north of the tropics), with a general migration of climate classes towards the pole.
Feng et al. (2014) uses the Trewartha version of the Köppen classification and quantifies the changes between present time and the projected end of the twenty-first century for RCPs 4.5 and 8.5. They find a global evolution towards warmer and drier climates. Figure 5 in Feng et al. (2014) shows the main regions of changes in the arid climate group. It compares well with Fig. 6b here: the large area in the central Asian region notably shows the cold to warm change in persisting SA conditions, while conversions from other types of climates (sub-humid or temperate) are shown in northeastern Brazil and the Mediterranean basin, for instance. Using the alternative aridity index approach, Feng and Fu (2013) have calculated a projected amplified expansion over the twenty-first century according to RCPs 8.5 and 4.5, using 27 climate models. They estimate that the global drylands are expected to expand by about 2100 ×103 km2 (+- 1500 ×103 km2) by the end of the twenty-first century according to RCP 8.5. We estimate that WSAR will increase by about 3254 ×103 km2 (+-1078 ×103 km2, Table 1); of which 1300 ×103 km2 (+- 800 ×103 km2, not shown) result from cold to warm conversions in the SA zones. Our net expansion of SA regions is therefore about 1900 ×103 km2, which is quite similar to the value found by Feng and Fu (2013).
5.3 On the validity of the methodologies used to anticipate the evolution of SA regions
Two major global changes in the future, warming and increasing atmospheric CO2 concentration ([CO2]), influence the climate-vegetation equilibrium in a way that the Köppen classification and the climate models partly fail to reproduce correctly.
Köppen’s aridity thresholds, for one thing, are based on T and P relationships that were empirically determined in the historical period to represent geographic patterns of arid and semi-arid forms of vegetation (Section 2.1). These mainly depend on the available water, hence on the relation between the precipitation and the water demand represented here by temperature-based Pth. As a result, the T factor drives conversions to semi-arid and arid classes through the rising of the Pth threshold. However, other factors than T drive the water demand, which is more often estimated with the potential evapotranspiration (PET). The Penman-Monteith equation, most commonly used to estimate PET, thus integrates the solar-radiation factor, among others. As shown by Scheff and Frierson (2014), the PET dependance on temperature is the highest in polar latitudes, while the radiation factor is more influent at the lower latitudes where WSA regions are typically located. In the Köppen classification, the differences of water demand are only modulated through the temperature, regardless of the radiation factor. For these reasons, keeping the aridity thresholds unchanged throughout future projections may lead to overestimating the impact of a temperature change in the future at a given latitude, while the level of solar-radiation, linked to the Earth inclination, does not change. This overestimation may account partly for the preponderance of the T effect in the future WSA surface change as shown in section Supplementary Materials 5.
Secondly, the major objection raised in the recent literature regards the effect of [CO2] on plants. Here, we differentiate between “atmospheric aridity” (diagnosed from 2m atmospheric variables) and “vegetation aridity”. Many plants may indeed increase the water use efficiency with increasing [CO2] (e.g. Donohue et al. (2013)). As a result, under higher [CO2] “atmospheric” and ”vegetation aridity” become somewhat decoupled, as greater “atmospheric aridity” does not translate into greater stress on vegetation. This could lead to over-estimating future aridification (Roderick et al. 2015; Milly and Dunne 2016). On the other hand, increased water use efficiency leads to decreasing total evapotranspiration (higher [CO2] increases stomatal closure, thus decreasing stomatal conductance). This results in a shift in the Bowen ratio, which warms and dries the overlying atmosphere (e.g. Swann et al. (2016) and Berg et al. (2016)), thus contributing to increasing “atmospheric aridity”. Because of these complex vegetation response and feedback, ecosystem shifts should not be directly inferred from atmospheric changes.
6 Conclusion
The main result of our paper is that the WSA domain will expand globally, and more specifically outside of its present tropical location. This increase is proportional to the projected future global warming in all scenarios and models. We have applied the well-known Köppen classification to outputs from 12 climate models forced with three socio-economic scenarios (RCP 2.6, 4.5 and 8.5), and analyzed the time evolution of WSAR from 1901 to 2100. Historical behavior was also reconstructed using observed atmospheric forcing. We show that WSAR have already increased in the past, in both observations and models, albeit with lesser magnitude when reconstructed from model outputs. This however is in line with existing literature.
In the future, WSA regions, frontiers between fully arid and sub-humid conditions, will experience both a poleward migration and an increase of the its global extent. WSAR are therefore expected to expand outside the tropical belt, many temperate regions being converted through both warming and drying into WSAR, although T has been shown to be the main driver. Many cold SA regions will become WSAR through warming. The use of the Köppen classification provides a direct picture of the different types of transition. This could be particularly helpful in communicating results to other fields of research or to stakeholders in development programs implemented in present and future WSAR.
Finally, one should be careful not to over-interpretate the shifting of a given bioclimatic class in terms of biome migration: in higher [CO2] conditions, new atmosphere-vegetation equilibrium are likely to appear. Thresholds set for the historical period may become less adequate in the future. Although the Köppen classification and the climate models have proven powerful tools to explore the future, further tuning is thus needed, where vegetation is involved, to account for future T and [CO2] conditions.
References
Berg A, Findell K, Lintner B, Giannini A, Seneviratne SI, Van Den Hurk B, Lorenz R, Pitman A, Hagemann S, Meier A et al (2016) Land-atmosphere feedbacks amplify aridity increase over land under global warming. Nat Clim Chang 6:869–874
Christensen JH, Kanikicharla KK, Marshall G, Turner J (2013) Climate phenomena and their relevance for future regional climate change. In: Stocker TF, Qin D, Plattner G-K, Tignor MM, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate Change 2013: the physical science basis. Contribution of Working Group I to the fifth Assessment of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, pp 1217–1308
Collins M, Knutti R, Arblaster J, Dufresne J-L, Fichefet T, Friedlingstein P, Gao X, Gutowski W, Johns T, Krinner G, Shongwe M, Tebaldi C, Weaver A, Wehner M (2013) Long-term climate change: projections, commitments and irreversibility, book section 12. Cambridge University Press, Cambridge, pp 1029–1136
Donohue RJ, Roderick ML, McVicar TR, Farquhar GD (2013) Impact of co2 fertilization on maximum foliage cover across the globe’s warm, arid environments. Geophys Res Lett 40(12):3031–3035
Feddema J (2005) A revised thornthwaite-type global climate classification. Phys Geogr 26(6):442–466
Feng S, Fu Q (2013) Expansion of global drylands under a warming climate. Atmos Chem Phys 13(10):081–10
Feng S, Hu Q, Huang W, Ho C-H, Li R, Tang Z (2014) Projected climate regime shift under future global warming from multi-model, multi-scenario {CMIP5} simulations. Glob Planet Chang 112:41–52
Fraedrich K, Gerstengarbe FW, Werner PC (2001) Climate shifts during the last century. Clim Chang 50(4):405–417
Fujino J, Nair R, Kainuma M, Masui T, Matsuoka Y (2006) Multi-gas mitigation analysis on stabilization scenarios using AIM global model. Energy J 27:343–353
Gleckler PJ, Taylor KE, Doutriaux C (2008) Performance metrics for climate models. J Geophys Res Atmos 113(D6). D06104
Hijioka Y, Matsuoka Y, Nishimoto H, Masui T, Kainuma M (2008) Global GHG emission scenarios under GHG concentration stabilization targets. J Glob Environ Eng 13:97–108
Huang J, Ji M, Xie Y, Wang S, He Y, Ran J (2016) Global semi-arid climate change over last 60 years. Clim Dyn 46(3-4):1131–1150
Ji M, Huang J, Xie Y, Liu J (2015) Comparison of dryland climate change in observations and CMIP5 simulations. Adv Atmos Sci 32(11):1565–1574
Johanson CM, Fu Q (2009) Hadley cell widening: model simulations versus observations. J Clim 22(10):2713–2725
Jylhä K, Tuomenvirta H, Ruosteenoja K, Niemi-Hugaerts H, Keisu K, Karhu JA (2010) Observed and projected future shifts of climatic zones in europe and their use to visualize climate change information. Weather, Climate, and Society 2 (2):148–167
Köppen W (1900) Versuch einer Klassifikation der Klimate, vorzugsweise nach ihren Beziehungen zur Pflanzenwelt. Geogr Z 6(11. H):593–611
Kottek M, Grieser J, Beck C, Rudolf B, Rubel F (2006) World map of the koppen-Geiger climate classification updated. Meteorol Z 15(3):259–263
Kravtsov S, Wyatt M, Curry J, Tsonis A (2015) Comment on atlantic and pacific multidecadal oscillations and northern hemisphere temperatures. Science 350 (6266):1326–1326
Lu J, Vecchi GA, Reichler T (2007) Expansion of the Hadley cell under global warming. Geophys Res Lett 34(6)
Milly P, Dunne K (2016) Potential evapotranspiration and continental drying. Nat Clim Chang 6:946–949
Mitchell TD, Jones PD (2005) An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int J Climatol 25 (6):693–712
Power SB, Kociuba G (2011) The impact of global warming on the southern oscillation index. Clim Dyn 37(9):1745–1754
Reynolds JF, Smith DMS, Lambin EF, Turner BL, Mortimore M, Batterbury SP, Downing TE, Dowlatabadi H, Fernández RJ, Herrick JE (2007) Global desertification: building a science for dryland development. Science 316 (5826):847–851
Riahi K, Grübler A, Nakicenovic N (2007) Scenarios of long-term socio-economic and environmental development under climate stabilization. Technol Forecast Soc Chang 74(7):887–935
Roderick ML, Greve P, Farquhar GD (2015) On the assessment of aridity with changes in atmospheric co2. Water Resour Res 51(7):5450–5463
Rubel F, Kottek M (2010) Observed and projected climate shifts 1901-2100 depicted by world maps of the koppen-Geiger climate classification. Meteorol Z 19 (2):135–141
Scheff J, Frierson DMW (2014) Scaling potential evapotranspiration with greenhouse warming. J Clim 27(4):1539–1558
Seidel DJ, Fu Q, Randel WJ, Reichler TJ (2008) Widening of the tropical belt in a changing climate. Nat Geosci 1(1):21–24
Swann AL, Hoffman FM, Koven CD, Randerson JT (2016) Plant responses to increasing co2 reduce estimates of climate impacts on drought severity. Proc Natl Acad Sci 113(36):10019–10024
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485
Van Vuuren DP, Edmonds J, Kainuma M, Riahi K, Thomson A, Hibbard K, Hurtt GC, Kram T, Krey V, Lamarque J-F, et al. (2011) The representative concentration pathways: an overview. Clim Chang 109: 5–31
Yukie H, Otto S (2011) Desertification: a visual synthesis. United Nations Convention to Combat Desertification (UNCCD)
Acknowledgements
We are very grateful to three anonymous reviewers whose valuable comments contributed to significantly improve this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rajaud, A., Noblet-Ducoudré, N. Tropical semi-arid regions expanding over temperate latitudes under climate change. Climatic Change 144, 703–719 (2017). https://doi.org/10.1007/s10584-017-2052-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-017-2052-7