Abstract
The effects of climate change are currently a red-hot issue in the scientific community. However, little attention has been paid to the effects of climate change on the wave climate and, in particular, on wave directionality. In this study, we developed a methodology of trend analysis and extrapolation of mean wave climate. We used the parameters of a typical wave rose: frequencies of wave height intervals and directional sectors. The trend over time was estimated by means of linear regression analysis after applying a transformation according to the nature of the (compositional) data. Then, the wave climate was extrapolated up to 2050 assuming the same previously estimated trend and part of the uncertainty was assessed with the bootstrapping technique. Additionally, to get an idea of the magnitude of the consequences of the identified trends, we carried out an impact assessment, in terms of coastal morphodynamics and harbour operability, comparing the present situation with the extrapolation. To assess the impact on coastal morphodynamics, we compared the gradients of long-shore sediment transport to evaluate possible changes in beach retreat/accretion tendency, and to assess harbour operability, we studied the possible impact on harbour agitation in three port case studies. This study was carried out on the Catalan coast (NW Mediterranean Sea) and was based on 40 nodes of 44 years of wave hindcast data. The main impacts on the wave climate were found to be a reduction in the waves coming from the north and northeast and an increase in events coming from the south. This apparently significant change in directionality could result in changes in the prevailing dynamic pattern along more than 70 % of the Catalan coast (e.g. some apparently stable beaches could become erosive) although these results have associated a large uncertainty and are not statistically significant. On the other hand, harbour agitation is expected to increase with statistical significance (by up to 18 % on average) because the studied ports, like most of Catalonia’s ports, are oriented towards the south-southwest.
Similar content being viewed by others
1 Introduction
Climate change has become a major focus of attention of the scientific community because of its potential impacts on our environment. In coastal engineering, one of the best-known consequences of the greenhouse effect and the resulting global warming is sea-level rise, mainly due to water mass increase (i.e. melting of ice sheets) and thermal volume expansion (e.g. Cazenave and Nerem 2004; Criado-Aldeanueva et al. 2008; Munk 2002), which can be aggravated by changes in storm surges (e.g. Lowe et al. 2001; Mousavi et al. 2011). However, this is not the only process of concern to coastal communities. As pointed out by various authors (e.g. Weisse and von Storch 2010), interactions with the atmosphere might produce some changes in wind and pressure patterns, which in turn can affect the pattern of another important coastal driver: the wave field. This situation can become critical because nowadays a high percentage of coasts are already eroding and some coastal infrastructures face multiple safety and operational problems (e.g. Coelho et al. 2009; Dickson et al. 2007; Sánchez-Arcilla et al. 2010).
Researchers currently use several different methods to study the impact of this phenomenon on the wave field. These methods can be divided into two main groups: i) trend analysis of long-term measured or reconstructed wave data (e.g. Hemer et al. 2008; Wang and Swail 2001, 2002) and ii) future projections obtained from climate models. At the regional scale, the latter method can be divided into statistical (e.g. Wang et al. 2004, 2010; Wang and Swail 2006) and dynamical (e.g. Grabemann and Weisse 2008; Lionello et al. 2008) downscaling. Each of these methodologies has its limitations (often computational cost vs. simplification assumptions), and the attribution problem (Weisse and von Storch 2010) often arises because natural variability, at different time scales, is combined with the possible impact of climate change. In addition, little attention has been paid to the changes on wave direction.
In the context of climate change, this study proposes a methodology for performing trend analysis of wave hindcast data in terms of a wave rose that combines wave height and direction. This methodology, which was partially applied by Casas-Prat and Sierra (2010a,b) for extreme (storm) conditions (analysing separately wave storminess and wave direction), allows to obtain future wave extrapolations without significant computational effort that can be used as an initial estimate, especially when high-resolution regional ensemble wave simulations are not available. It focuses on the Catalan coast, which is located along the NW Mediterranean Sea but although the methods presented were applied to this specific region, they have general applicability and could be used in other areas of the world.
Two facets of the potential impacts of the resulting future wave climate were addressed in this study. First, the effects on coastal dynamics were studied in terms of changes in long-shore sediment transport (LST) and, in turn, in the tendency towards erosion or accretion. Second, the possible increase in harbour agitation, which might result in a decrease in operational capacity, was analysed in three selected harbours along the Catalan coast.
In Section 2, the wave data is presented. In Section 3, the case studies are briefly described. In Section 4, the methodology is explained in detail. In Section 5, the results are presented and discussed, and finally, in Section 6, the conclusions of our study are summarised.
2 Data
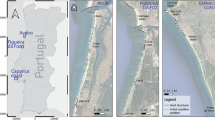
The present study is based on the 44-year hindcast wave climate database (1958–2001) from the European HIPOCAS project (Guedes Soares et al. 2002). This wave data set was obtained with the WAM model and forced by the wind output of the regional atmospheric model REMO, which in turn was forced by the global re-analysis data of NCEP. The HIPOCAS database has been extensively validated for wind, wave and sea-level parameters (Musić and Nicković 2008; Sotillo et al. 2005). This simulation, like most, has some limitations in terms of properly reproducing certain storm events but it generally reproduces mean values quite well (Ratsimandresy et al. 2008). In addition, it offers homogeneous long-term data and high spatial coverage as compared to single-point observations (e.g. buoys). This paper uses the significant wave height (H s ) and the mean wave direction (θ) obtained at 40 selected nodes along the Catalan coast (see Fig. 1), with a spatial and temporal resolution of 12.5 km and 3 h, respectively.
3 Case studies
3.1 Catalan coast
A good review of the wave climate along the Catalan coast is given by Sánchez-Arcilla et al. (2008). The Catalan Sea (NW Mediterranean Sea) is bounded by this coast, the south of France and the Balearic Islands. In this area, the local topography has a significant impact on the wind climate and, therefore, on the wave field. The wind generally ranges from low to medium intensity, but some extreme synoptic events occur. The directional distribution of winds produces a predominance of waves coming from the east and southeast, which are characterised by stronger winds and a longer fetch (of about 600 km). In the most northern area, a considerable proportion of waves also comes from the north.
At the broad regional scale, the Catalan coast stretches about 580 km, but when measured at higher definition, it is found to be approximately 780 km long. Sánchez-Arcilla et al. (2007) carried out an extensive study, ordered by the Catalan Government, of the characteristics of this coast. That study serves as a useful database for further assessment analysis in this area, as for example in the present study. In terms of beach typology, the coast can be roughly divided into two parts. The northern part (Costa Brava, see Fig. 2) mostly consists of beaches nestled between cliffs. The rest of the coast mainly comprises low-lying beaches (with the exception of deltas and occasional abrupt cliffs), which in turn can be divided between sandy and gravelly beaches. In the northern portion of this second part (e.g. Maresme, see Fig. 2), the beaches are generally narrow, with relatively high slopes and gravel or coarse sand originating in the coastal mountains (oriented along a NE axis, parallel to the coast, 30–60 km from the shoreline). In contrast, in the portion of the coast to the south of Barcelona (e.g. Costa Daurada), sediment comes from the pre-coastal depression (which is 100 km long and 20 km wide and lies between the coastal and pre-coastal mountain ranges, the latter lying parallel to the coastal range and further inland), resulting in very fine sand, soft slopes and wider beaches. The median particle sizes of these two types of low-lying beaches are 0.7 mm and 0.4 mm, respectively, calculated using the sediment database obtained by Sánchez-Arcilla et al. (2007).
The largest Catalan delta (Ebre delta, see Fig. 2) is located on the southern part of the coast. This area of high ecological value covers about 32,000 ha, with half of that area lying at an altitude of less than 0.5 m (Alvarado-Aguilar 2009). It is one of the most important wetlands in the Mediterranean, after the Nile and Rhone deltas. The Ebre delta was built up by the surplus of sediment discharge, but it is currently in a critical situation as both sediment input and river discharge have decreased drastically.
The European EUROSION project (2002–2004) classified Catalonia as an area highly exposed to coastal erosion, with 33 % of the coast being eroded on average. This classification took into account several factors, including shoreline instability and the growth of coastal urbanisation over the past few years, among others. The study also revealed that a considerable portion of the land under the influence of coastal erosion is urbanised, industrial and/or of high ecological value, which enhances the risk of a possible erosion event. Compounding the risk, about three million people, or 40 % of the Catalan population, live in coastal areas. Figure 2 shows the classification of the Catalan coast in erosive, stable and accretive, adapted from the EUROSION project, in which most of the Catalan coastline is exposed to erosion.
3.2 Harbours selected
As mentioned in the Introduction, three harbours—Blanes, Fòrum and Tarragona—were selected to study the impact of possible changes in the incoming wave pattern on harbour agitation. Of the 47 harbours on the Catalan coast, these three were selected for their location, type and size. Figure 1 shows that they are evenly spaced along the Catalan coast. The Blanes and Fòrum ports are small. Blanes, the northernmost harbour, is both a marina and a fishing port, whereas the Fòrum port, located close to Barcelona, is a marina that exclusively serves leisure crafts. Finally, Tarragona is a commercial port 4.5 km long and 2 km wide located about 100 km to the south of Barcelona, and it is one of the most active ports in the Mediterranean in terms of cargo and vessel traffic (Mestres et al. 2010). According to the Catalan Government’s 2007–2015 Port Plan, one of the most common problems affecting the functionality of Catalan ports is the high degree of agitation inside them. It is therefore necessary to study the possible intensification of this phenomenon, which is already occurring in some cases.
4 Methodology
The methodology in this study comprises three main aspects: i) present and future wave climate, ii) impact on coastal dynamics, and iii) effects on harbour agitation.
4.1 Present and future wave climate
The wave climate of each selected node (of a total of 40 nodes) was characterised by a wave rose (see Fig. 3), which is a wave graphic tool with several engineering and scientific applications. Eight 45º directional sectors (Δθ i ) were considered, each centred on one of the four cardinal and four ordinal directions: north (N), northeast (NE), east (E), southeast (SE), south (S), southwest (SW), west (W) and northwest (NW). In turn, for each incoming direction, the waves were also grouped on the basis of the magnitude of the significant wave height in metres [0–1, 1–2, 2–3, 3–4, >4]. To calculate these eight directional frequencies (\( {f_{{\Delta {\theta_i}}}} \)) and the frequency of each group of H s and direction (\( {f_{{\Delta {H_i}/\Delta {\theta_j}}}} \)), we used Eq. 1, which is based on the Bayesian inference of Agresti (2002).
where k θ = 8 and k H = 5 are the number of classes and \( {n_{{{\theta_i}}}} \), \( {n_{{\Delta {H_j}/\Delta {\theta_i}}}} \) and n total are the amount of data per each sector Δθ i , per each group ΔH j subjected to a certain Δθ i , and in total. The product of frequencies of Eq. 1 is the estimated total probability of occurrence of each combination of Δθ i and ΔH j , denoted as \( {f_{{\Delta {H_j},\Delta \theta i}}} \) (see Eq. 2).
In contrast to the maximum likelihood estimator (e.g. \( {n_{{\Delta {\theta_i}}}}/{n_{{total}}} \)), the frequencies estimated by Eq. 1 never reach a value of zero. As explained by Casas-Prat and Sierra (2010b), this property is useful for both theoretical and practical reasons for further applications (e.g. taking logarithms). These authors also noted the limitations of this method when it is applied to a limited number of data (e.g. a small number of storms) for which Casas-Prat and Sierra (2010b) recommended to use a different approach to estimate the frequencies, but this is not the case here because \( {n_{{total}}} \) and \( {n_{{\Delta {\theta_i}}}} \) are generally high enough and therefore the Agresti formula can be followed. The present wave climate was thus obtained by simply calculating the aforementioned frequencies: Eq. 1 was applied for all data for the period 1958–2001. Thus, 40 wave roses were obtained, representing the mean wave climate during the second half of the 20th century. This climate, denoted in this paper as the “present” situation, corresponds to the 40 node locations illustrated in Fig. 1.
A future wave climate for the year 2050 was extrapolated based on the tendency found for the 44-year wave hindcast time series. In the context of climate change, this is obviously a first approximation because it does not consider explicitly the greenhouse effect and it assumes the same trend over time. Briefly, the procedure for each node was as follows: i) a wave rose, \( {f_{{\Delta {\theta_i}}}}(t) \) and \( {f_{{\Delta {H_j}/\Delta {\theta_i}}}}(t) \), was calculated for each year using Eq. 1, t = 1958,…,2001; ii) its temporal trend corresponding to the 44 years of data was estimated by statistical analysis; and iii) the wave climate in 2050 was obtained by extrapolating such trend.
The statistical analysis (ii) consisted of a classical linear regression analysis but implemented after applying a transformation to the data. The annual frequencies obtained in (i) are compositional data (Aitchison 1982) because they are quantitative descriptions of the parts of some whole and therefore there is an inherent relation (constant sum) between them, which can be mathematically defined in a simplex space. As noted by Pawlowsky-Glahn and Egozcue (2006), a conversion might be done before performing any statistical analysis based on the covariance matrix, such as regression analysis. Otherwise, the results are clouded by spurious effects. In this study, the isometric log-ratio (ilr) transformation (Egozcue et al. 2003) was used (see Eq. 3). Generally speaking, this transformation translates k frequencies {f 1 ,…,f k } into k−1 coordinates {y 1 ,…,y k−1 } on an orthonormal basis in a real vector space \( {\Re^{{k - 1}}} \), obtained from sequential binary partition (R i , S i ). The conversion can be expressed as the log ratio between the geometric mean of each partition \( \left( {g\left( {{f_{{ \in {R_i}}}}} \right),g\left( {{f_{{ \in {S_i}}}}} \right)} \right) \) multiplied by a normalising factor a(r i ,s i ).
where r i and s i are the number of elements in each partition. The results in terms of the frequencies are fairly insensitive to the chosen partition. In this study, such a partition for wave direction was done as follows: 1) N, NE, E, SE, S, SW vs. W, NW; 2) N, NE, E vs. SE, S, SW; 3) N vs. NE, E; 4) NE vs. E; 5) SE vs. S, SW, 6) S vs. SW and 7) W vs. NW. After some basic algebraic transformations, for a year t Eq. 3 can be rewritten as Eq. 4:
where \( {\mathbf{y}}(t) = {\left[ {{y_1}(t),...,{y_{{k - 1}}}(t)} \right]^T} \), \( {\mathbf{f}}(t) = {\left[ {{f_1}(t),...,{f_k}(t)} \right]^T} \) and M is a matrix of known coefficients of (k−1, k) dimensions. In this study, Eq. 4 was applied for \( {\mathbf{f}}(t) = {{\mathbf{f}}_{{\Delta \theta }}}(t) = {[{f_{{\Delta {\theta_1}}}}(t),...,{f_{{\Delta {\theta_{{{k_{\theta }}}}}}}}(t)]^T} \) and \( {\mathbf{f}}(t) = {{\mathbf{f}}_{{\Delta H/\Delta {\theta_i}}}}(t) = {[{f_{{\Delta {H_1}/\Delta {\theta_i}}}}(t),...,{f_{{\Delta {H_{{{k_H}}}}/\Delta {\theta_i}}}}(t)]^T} \) for i = 1,…, k θ , thus obtaining y ∆θ(t) and \( {{\mathbf{y}}_{{\Delta H/\Delta {\theta_i}}}}(t) \), respectively.
Once the coordinates, which can be assumed to be normally distributed, were obtained, a classical linear regression analysis was carried out for each component (see Eq. 5). Therefore, for each wave rose, 35 simple regressions were computed: (k θ −1) + (k θ −1)·(k H −1) = 7 + 7·4 = 35. We fitted a linear trend (in terms of the coordinates) rather than a more complex tendency, based on the principle of parsimony. As the real (physical) wave climate evolution over time is (still) unknown, we assumed a simple trend shape.
Finally, the 2050 wave climate extrapolation (iii) consists of a wave rose for each node constructed with \( {{\mathbf{\widehat{f}}}_{{\Delta \theta }}}(t = 2050) \) and \( {{\mathbf{\widehat{f}}}_{{\Delta H/\Delta {\theta_i}}}}(t = 2050) \). These were calculated by using the estimated coefficients of Eq. 5 and the inversion of Eq. 4 (for t = 2050), which results in the following general equation:
where C is the closure operation to achieve the relationship \( \sum\limits_{{i = 1}}^{{{k}}} {{{\widehat{p}}_i}} = 1 \) and \( \widehat{{\mathbf{y}}}(t) \) are obtained using Eq. 5. Note the conceptual difference between f(t) and \( \widehat{{\mathbf{f}}}(t) \) (and, correspondingly, between y(t) and \( \widehat{{\mathbf{y}}}(t) \)). The former, f(t), is a direct measure of the data and it is simply obtained by Eq. 1 for a single year t (1958 ≤ t ≤ 2001), whereas the latter, \( \widehat{{\mathbf{f}}}(t) \), is an approximation of the frequency vector for a year t and is obtained according to the linear regression model of Eq. 5 and the subsequent inverse transformation of Eq. 6. However, to simplify the notation, f(t), and consequently f ∆θ(t) and\( {{\mathbf{f}}_{{\Delta H/\Delta {\theta_i}}}}(t) \), will refer to both types of calculations, depending on the context: normally it refers to f(t) for 1958 ≤ t ≤ 2001 and to \( \widehat{{\mathbf{f}}}(t) \) for t > 2001.
4.2 Coastal dynamics
The impact on coastal dynamics was determined by comparing the contribution of each node’s present and future (2050) wave climate to the total long-shore sediment transport (LST), which is one of the most important coastal morphodynamic processes, and, in turn, to the tendency towards beach retreat or accretion.
An excellent review of the literature on the most commonly applied formulas for calculating LST was given by Bayram et al. (2007). Those authors also proposed a new formula—the “Bayram formula”—based on principles of sediment transport physics. They compared the results of various LST formulas with six high-quality data sets on hydrodynamics and sediment transport collected under both field and laboratory conditions. Their new formula provided the best results in terms of both scatter and percentage of data with discrepancy. Worse results were obtained by, in order of agreement, the formulas of Kamphuis (1991, 2002), Inman and Bagnold (1963), and CERC (1984).
In fact, the Bayram formula can be considered an improvement over the well-known CERC (1984) formula (see Eqs. 7 and 8). The CERC formula is still widely used in conditions where current-induced transport is not important (e.g. not in estuaries), but it has a major handicap in its empirical coefficient K: in order to obtain reasonable results, K must be previously calibrated with measured data and applied to similar breaker types. In addition, the proven influence of grain size on LST (King 2005) is not accounted for in the CERC formula.
Therefore, given its superiority in terms of its ability to predict LST in different contexts, and the relative simplicity of the parameters involved, we used the Bayram formula in the present study. As mentioned above, under certain ideal physical conditions, Bayram et al. (2007) reduced their new formula to the CERC formula (Eq. 7) with a coefficient K in terms of ε, the portion of wave energy used to transport sediment:
where Q is the LST, ρ is the density of water (ρ = 1026 kg/m3), ρ s is the density of sand (ρ s = 2650 kg/m3), a is the porosity index (a = 0.4), γ b is the breaker index (γ b = 0.78), cf is the friction coefficient (cf = 0.005), H s,b is the representative significant wave height at breaking, C g,b is the group velocity at breaking, and α b is the angle between wave crest and coastline at breaking. To estimate ε, Bayram et al. (2007) provided a relation between ε and wave and sediment properties (H s,b , T p and w s ) (see Eq. 9), which was obtained by fitting the six aforementioned high-quality data observations:
where T p is the peak wave period and w s is the particle fall speed. Therefore, LST was in fact calculated using the CERC formula but considering a coefficient K, which depends on both wave and sediment properties. The settling velocity, w s , was calculated using the formula developed by Jiménez and Madsen (2003) (see Eq. 10), which relates w s to the nominal diameter (d N ):
where d N = 0.9d S , being d S the sieving diameter, obtained from Sánchez-Arcilla et al. (2007), and v is the kinematic viscosity (v = 10−6 m2/s).
Nevertheless, Eq. 7 only includes the LST produced by a single regular wave represented by H s,b . In order to involve the whole wave climate characterised by the wave roses obtained according to Section 4.1 (for present and future conditions), Eq. 11 was used to estimate the mean annual net LST (Q annual ) assuming that the amount of total sediment is not limited:
where \( {Q_{{\Delta {H_j}/\Delta {\theta_i}}}} \) was computed by using Eq. 7, except for the directions that do not affect the coast at a particular location, in which case \( {Q_{{\Delta {\theta_i},\Delta {H_j}}}} = 0 \). Since \( {Q_{{\Delta {\theta_i},\Delta {H_j}}}} \) is normally expressed in terms of volume transported per second, a constant β = 3.15·10−7 was added for unit conversion. Note that the dependency on time was only included in \( {f_{{\Delta {H_j},\Delta \theta }}}_i \) (see Eq. 2) and thus in \( {f_{{\Delta {\theta_i}}}} \) and \( {f_{{\Delta {H_j}/\Delta {\theta_i}}}} \), calculated as explained in Section 3.1 (see Fig. 4).
To calculate \( {Q_{{\Delta {H_j}/\Delta {\theta_i}}}} \), for each interval ΔH j (defined in Section 3.1), the representative parameter of H s for intermediate-deep water was taken as the centred value of such a interval, with the exception of the largest group, for which a representative value of 5 m was considered, i.e., H s,0 = [0.5, 1.5, 2.5, 3.5, 5] m. Then, the values at breaking , H s,b , were obtained by linear wave propagation (using Snell’s law) until de depth of breaking (h b ), taking into account the refraction and shoaling processes and assuming a constant mean wave period (T m ). The wave period was empirically obtained for each direction by fitting to the hindcast data a relation \( {{T}_{m}} \propto \sqrt {{{{H}_{s}}}} \). The peak period of Eq. 9 was calculated as T p = 1.15 T m as suggested by Puertos del Estado (1992) for this area.
As the aim of this study is to perform a regional scale impact assessment, some additional assumptions were made to simplify the irregularity of the coast. First, in order to have approximate values of the coastline angle, the Catalan coast was divided into six straight stretches (see Fig. 5). The Roses cape (north) and the Ebre delta (south) were not considered here because those parts of the coastline are highly variable in space and therefore require a more local study and, additionally the Roses cape (and surroundings) is an area with a large percentage of rocky coast (see Section 3.1) for which the LST formulas, as the Bayram formula, do not apply. Thus, only wave data from nodes 7 to 34 were used (see Fig. 1). The remaining (studied) coast was assumed to be sandy and the presence of occasional abrupt cliffs or structures was neglected.
Such a configuration of the coast (receptor) was assumed to be permanent in time and therefore we only considered the possible change of the forcing driver (waves). In a local study, not considering the feedback between waves and coastal morphology might introduce an important error which will increase with time. But this error is not significant in the present study performed at regional scale because the possible beach plant variation due to this feedback is negligible compared to the assumptions made to simplify the coastline.
In addition, as mentioned in the Introduction, the impact on coastal dynamics was also characterized by the tendency towards beach retreat/accretion, which was estimated based on the continuity equation (Eq. 12), as similarly done by Hemer (2009). dη/dt was calculated for the cells delimited between two consecutive node projections perpendicular to the coast.
being d the closure depth, which can be calculated by Eq. 13 (Hallermeier 1978):
where H s,12h/y is the significant wave height exceeded 12 h per year. ΔQ/Δx is the gradient of LST which is approximated by the difference between two consecutive values of Q annual in space divided by the distance (Δx) between those values. To estimate Δx, the linear distance between projected nodes was used as outlined in Fig. 5.
We want to emphasise that due to the assumptions made and the relatively long cells (~10 km), the results obtained by Eq. 12 were considered in a qualitative manner. The aim was not to predict the local evolution of the coastline but to estimate in mean terms whether the rate of sediment gain/loss in each cell within the active zone (h<d) will tend to increase, decrease or remain constant. To do this, the values obtained for dη/dt were used to classify the coastal stretches in three different states (as in Fig. 2): stable, erosive and accretive. The threshold used to delimit these states was calculated so as to minimise the discrepancy between the results we obtained for the present tendency and the ones of the EUROSION project (Fig. 2), even though these two datasets have different time spans and spatial scales. In this paper, the present situation refers to the average for the period 1958–2001, whereas the EUROSION project assessed the actual situation for the project period (2002–2004).
4.3 Harbour agitation
To investigate the possible impact on harbour agitation, three representative ports along the Catalan coast were selected (see Fig. 1 and Section 4.2). For each port, the nearest HIPOCAS node was considered: node 14 for Blanes, node 20 for Fòrum and node 30 for Tarragona. The wave roses of these nodes, obtained as explained in Section 3.1 for the two time scenarios (present and future), represent the offshore wave climate conditions at each port.
First, the wave directions capable of affecting the selected harbours were determined. These directions are E, SE and S for Blanes and Fòrum and E, SE, S and SW for Tarragona. For each direction, following the approach detailed in Section 4.1, five wave heights were available (four of which, 0.5 m, 1.5 m, 2.5 m and 3.5 m, corresponded to half of the selected interval, with the last one corresponding to an assumed value of 5 m) and a mean wave period was computed for each wave height.
For the three studied cases, the five H s,0 and T m pairs determined for each direction were propagated, employing linear wave theory, from the node where they were computed to the outer boundary of the numerical agitation model. There, new significant wave heights and wave directions, due to the shoaling and refraction of the waves, were obtained and denoted as H s,ext . These new values were input into the Boussinesq-type model (González-Marco et al. 2008) that was used to study the agitation inside the harbour due to its ability to reproduce processes such as diffraction and reflection, which, in addition to shoaling and refraction, are very important there. The grid sizes were Δx = 5 m at Tarragona, Δx = 3 m at Fòrum and Δx = 2 m at Blanes.
After the numerical simulation, a value of H s was obtained at each grid point inside the harbour and denoted as H s,int (x,y). Then, an average of H s,int (x,y) was computed for the whole harbour for each simulation and denoted as H s,int . In addition, considering the ratio between H s,int and H s,ext , an overall agitation coefficient, denoted as k a , was obtained.
Finally, an annual mean significant wave height, \( \overline {{H_{{s,int}}}} \), was computed for each harbour using Eq. 14:
where \( {H_{{s,in{t_n}}}} \) is the average significant wave height for each simulation n (associated with a particular combination of wave height interval j and direction i); t n is the time (in days) that this direction and wave height interval occurs in a year; N is the number of simulations (15 for Fòrum and Blanes and 20 for Tarragona, corresponding to five wave height intervals and three or four directions); and \( {f_{{\Delta {H_j},\Delta \theta }}}_i \), or f n , is the frequency of occurrence of a wave height interval and direction associated with the simulation n (see Eq. 2). As mentioned above, the range of directions considered here is limited to waves capable of entering the port (\( i = {k_{{{\theta_1}}}},...,{k_{{{\theta_2}}}} \)). For example, for the Tarragona port, θ 1 = 90º (E) and θ 2 = 225º (SW) and therefore i = 3,…,6.
If f n is substituted by the values obtained for the period 1958–2001 (see Section 3.1), the resulting \( \overline {{H_{{s,int}}}} \)is the mean wave height in the present conditions, whereas if f n is substituted by the values extrapolated for 2050, \( \overline {{H_{{s,int}}}} \)is the mean wave height estimated for that year. The impact of long-term changes in wave climate on harbour agitation was estimated by comparing these two values.
4.4 Uncertainty analysis
The role of uncertainty is very important in a long-term analysis in the context of climate change. In this study, the bootstrapping technique was used to bound the frequencies of the 2050 extrapolated wave roses. Such a technique is simple but it is quite powerful with many applications. In fact, for the wave storm energy content, Casas-Prat and Sierra (2010a) compared the confidence bounds obtained by bootstrapping and a more complex Bayesian technique and they found quite similar results.
The procedure for the uncertainty analysis can be summarised as follows. For each node and each original sample of the pairs [t, f ∆θ (t)] and \( [t,\;{{\mathbf{f}}_{{\Delta H/\Delta {\theta_i}}}}(t)] \), obtained after applying Eq. 1 for each single year t, for 1958 ≤ t ≤ 2001, n boot (n boot = 1,000) samples of the sample length were randomly generated allowing repetition. Then, for each of these samples, the trend and the corresponding 2050 extrapolation was estimated according to the methodology explained in Section 4.1 (Eqs. 4, 5 and 6) thus obtaining n boot samples of f ∆θ (t = 2050) and \( {{\mathbf{f}}_{{\Delta H/\Delta {\theta_i}}}}(t = 2050) \), and, in turn, n boot samples of the total probability of occurrence as their product (see Eq. 2): \( {{\mathbf{f}}_{{\Delta {H_j},\Delta \theta }}}_i(t = 2050) \). Such samples served not only to calculate the 95 % marginal confidence intervals of the frequencies of the extrapolated wave roses (as their 0.025 and 0.975 percentiles) but also to assess the uncertainty of the impact on coastal dynamics and harbour agitation: the n boot samples of \( {{\mathbf{f}}_{{\Delta {H_j},\Delta \theta }}}_i(t = 2050) \)were inserted in Eqs. 11 and 14 to obtain, respectively, n boot samples of Q annual and \( \overline {{H_{{s,int}}}} \), and their associated confidence intervals for the future extrapolation.
As explained in Casas-Prat and Sierra (2010b), this methodology only considers uncertainty related to the variability of the data and does not consider, for example, uncertainty related to the extrapolation method. Therefore, this uncertainty is a lower bound of the total uncertainty.
5 Results and discussion
5.1 Present and future wave climate
As explained in Section 4.1, the wave climate was characterised in terms of wave roses for the time period 1958–2001 (present) and for 2050 (future extrapolation). Figure 6 shows an example (node 2) of the linear regression analysis performed in terms of the coordinates, see Eq. 3, (left) and its transformation into the frequency domain (right). In the left panel, the linear trends of the 7 coordinates (obtained after the sequential binary partition explained in Section 4.1) are plotted, whereas in the right panel, such linear trends are expressed in terms of the 8 original (annual) directional frequencies (N, NE, E, SE, S, SW, W and NW). Therefore, although the plotted lines in the right might seem to follow a linear trend, they are not straight lines. Such lines are discretely obtained year by year (1958 < t < 2001) after applying Eq. 6 which is an inversion of the ilr transformation. We want to outline that without previously transforming the data and fitting linear trends directly to the frequencies, one can obtain nonsense results such as negative frequencies or values larger than unity. On the other hand, as mentioned in Section 4.1 the results in terms of frequencies are fairly insensitive to the chosen partition: 1) N, NE, E, SE, S, SW vs. W, NW; 2) N, NE, E vs. SE, S, SW; 3) N vs. NE, E; 4) NE vs. E; 5) SE vs. S, SW, 6) S vs. SW and 7) W vs. NW.
Example of results of trend estimation for the node 2. Left: linear regression applied to the 7 coordinates (y 1,…,y 7). Right: trend in terms of the frequencies of the 8 directions (f 1,…,f 8). Although frequency trends look linear, they follow a non-linear behaviour obtained after undoing the ilr transformation (see Eq. 6). See text for further explanation
In this case, for example, the value of y 2 contrasts the presence of N, NE and E waves (f 1, f 2, f 3) versus SE, S and SW waves (f 4, f 5, f 6). The result of y 2 being positive is expected because it means that the amount of waves coming from N, NE and E is larger than from the sector comprised by SE, S and SW directions, as illustrated in Eq. 15.
Although the magnitude of y does not always have a straightforward physical interpretation, it serves to inter-compare the coordinates’ results. For instance, y 1 is obviously greater than y 2 because y 1 compares the whole range of predominant directions from N to (clockwise) SW against W and NW waves, which are clearly in a minority.
Consequently, the tendency of y 2 to decrease can be interpreted as a reduction in the number of “east-northerly” waves as compared to the “southerly” ones. After undoing the transformation, we realise that, more precisely, a clear tendency to decrease is found for N waves (f 1 ) in contrast to the tendency of rising of S and SE waves, which agrees with the abovementioned reasoning of y 2 evolution. Instead, y 1 fairly remains constant over time, which is reasonable since the ratio of the two groups of compared waves is importantly limited by the coastal configuration.
Extrapolating the trends, the wave roses for 2050 were obtained. Figure 7 shows the results for the nodes 2, 14, 20 and 30 (see Fig. 1), which are intended to be representative of most nearshore locations along the Catalan coast. A comparison of the proportions of each H s partition between present and future scenarios reveals that the magnitude of the wave climate either does not change significantly or that it decreases slightly (e.g. node 2 for N direction). Therefore, the amount of annual wave climate energy seems to remain practically constant. In fact, more significant differences can be seen in the distribution of frequencies among the directions. Node 2 undergoes a significant decrease in N waves (from 36 % to 26 %) whereas S and SE waves tend to increase (from 23 % to 30 % and from 13 % to 20 %, respectively) being consistent with Fig. 6. For nodes 14 and 20, for which the presence of N waves is residual due to the geographic location, an important relative decrease is seen in the NE direction (between 35 % and 60 %); this is compensated by a lower but homogeneous increase in the SW, S and SE directions (up to 30 %). The S frequency for node 30 rises as well (from 31 % to 37 %), but in this case the reduction in the other components is spread out, rather than being concentrated in one direction.
Such a N reduction is in qualitatively agreement with the results obtained by Najac et al. (2011). They applied a mixed statistical-dynamical downscaling based on 14 general circulation models’ projections and found a decrease of the westerly, north-westerly and northerly winds (main forcing of waves) over the southeast of France, which may be directly linked to the obtained change in the directional distribution of waves in the NW Mediterranean.
To assess the significance of the changes found in terms of directional frequency, Fig. 8 illustrates, for the same nodes as in Fig. 6, the 95 % marginal confidence intervals for the 2050 extrapolations (circles), which accompany the expected frequencies for 2050 (continuous line) as compared to the mean values of the period 1958–2001 (dashed line). The n boot bootstrapped samples (in grey) are also plotted. Their envelopes delimit a high-confidence region, which visually integrates the uncertainty between sectors. For example, a highly curved envelope between two consecutive extrapolated frequencies indicates that extreme values of these frequencies have a low probability of occurring simultaneously in the same considered time period. Although the uncertainty is considerable, in several cases the present situation is located close to the confidence limits of the future extrapolation, which means that the probability of change is high. For example, for node 2 the upper bound of the N frequency in the 2050 extrapolation overlaps the frequency obtained for the period 1958–2001, which indicates a 97.5 % probability of N events tending to decrease. A similar situation—but in the opposite direction—occurs for S waves.
Figure 9 shows, again for the same nodes of Fig. 7, the marginal evolution of the S frequency (f S) and its extrapolation up to 2050 using the methodology described in Section 3.1. Thus, the extrapolations and their uncertainties are discretely obtained year by year (as in right panel of Fig. 6). The uncertainty is considerable, partly due to the large interannual variability: during the period 1958–2001. For example, for node 30, f S ranges from 25 % (year 1982) to 37 % (year 2001) and the 95 % confidence interval for the 2050 extrapolation ranges approximately from 30 % to 45 % (with an expected value of 37 %), including the possibility of no significant change. An increasing scenario is more probable, however, and with 80 % confidence the range of 2050 extrapolations is above the mean frequency for the period 1958–2001. Obviously, the uncertainty associated with the extrapolated value increases over time; and, for instance, for a near future (2020) the uncertainty is halved. Similar results were found for the other three nodes of Fig. 9, being the uncertainty associated to node 14 somewhat lower. The relative increase of f S between the expected value for 2050 and the mean situation for the period 1958–2001 is 29 % for node 2, 22 % for 14 and 19 % for 20 and 30.
A comparison of the present results with those obtained by Casas-Prat and Sierra (2010b) under stormy conditions shows that the directional trends in the present study are similar, but that the average uncertainty is lower, partly because the data set is larger.
5.2 Impact on coastal dynamics
The frequencies obtained in Section 5.1 were used to study the impact on coastal dynamics. Since the first two groups (0–2 m), and in particular less than 1 m, comprised most of the data, a sensitivity analysis with partitions of 0.5 m (rather than 1 m) was carried out. The results for sediment transport (not shown here) were very similar; therefore, to simplify the analysis, the initial consideration of partitions of 1 m was followed. A sensitivity analysis of the LST formula was also carried out: the Kamphuis (1991, 2002) and CERC (1984) equations were also applied in addition to the Bayram formula. With the Kamphuis formula, the results were quite similar, though slightly higher than with the Bayram formula. In contrast, the CERC equation with the typical K coefficient of 0.39 recommended by the CERC’s Shore Protection Manual (1984) considerably overpredicted the results (by a factor of 10). This comparison once again underscores the need to calibrate the K coefficient, as other studies have demonstrated.
Figure 10 compares the results of Q annual obtained by the Bayram formula for the period 1958–2001 and for t = 2050. In addition, the 95 % and 80 % confidence intervals are plotted. As explained in Section 4.2, these results were obtained by computing the LST corresponding to each combination of wave height interval and direction, and balancing them to obtain the net LST (see Eq. 11). Positive values of Q annual indicate that the net LST direction is from N to S and vice versa. These Q results are ordered from N to S according to their perpendicular projections to the coast (see Fig. 5) but, to avoid confusion, the node number in the x-axis is the same as in Fig. 1. The spatial distribution of Q annual for the 2050 extrapolation is similar to that of the period 1958–2001; Q annual can therefore be said to be more or less translated to lower values. In some locations, moreover, the reduction is such that even negative values of Q annual are obtained, meaning net LST in the direction opposite to the present general pattern on the Catalan coast. This translation is not exactly constant over space, however; the change is less pronounced along the southern Catalan coast. This decrease in the net LST values is explained by the reduction in the frequency of waves coming from the N and NE (which generate southward LST, or positive values herein) and the increase in the frequency of waves coming from the SE, S and SW (which generate northward LST, or negative values herein).
The negative values of net LST are located in the area around Barcelona and in the northern part of the studied domain. Their consequences might be important because a change in net LST sign can produce, on the one hand, reorientation and/or destabilisation of the shoreline and, on the other, siltation of harbour entrances. However, the uncertainty analysis for Q annual exhibits no statistical significant change at 95 % level since the confidence intervals of 2050 extrapolation includes the estimation of the period 1958–2001 (not the case for some nodes with a reduced interval of 80 % though). Such a large uncertainty can be partly explained by the large sensitivity of LST formulas (in general) to small changes in wave climate and the consequent large interannual variability of Q annual , which, in turn, outline the uncertainty still present in the prediction of longshore sediment transport under current conditions, as pointed out by Sutherland and Gouldby (2003). The mean values of net LST calculated for the present situation are reasonable since not only the order of magnitude is correct but also their maximum value as well. For the period 1958–2001, Q annual is up to 40,000 m3/year, which is pretty close to recent estimated values of Q annual that reach up to 50,000 m3/year (Sole et al. 2010). Such differences are small in the context of LST calculation (Bayram et al. 2007) and in such a large scale.
Nevertheless, certain features of the results reveal some of the limitations of the methodology. For example, some sudden changes between two consecutive nodes are excessive and unrealistic. The reason is probably the simplification of the coast, i.e. sudden changes in the coastline angle between consecutive stretches, or differences in the distance between the nodes and the coast. For instance, node 9 is considerably nearer to the coast than node 10 is. For node 10, then, the final Q annual value theoretically has greater error, as it involves a longer trajectory of the simple linear wave propagation method until breaking. For this reason, the results for the nodes closest to the coast are considered more reliable. This consideration is especially important in the calculation of beach retreat/accretion (dη/dt, see Eq. 12) along the coast: if two projections are very close to one another, the one coming from the node further from the coast is not considered for the calculation of beach erosion/accretion.
Figure 11 shows the results of beach erosion and accretion along the Catalan coast for the two time scenarios considering the most probable situation. Due to the aforementioned limitations related to the methodology and the available data, these results are presented in a qualitative manner and stretches are classified in three stages: erosive, stable or accretive (as explained in Section 4.2). Intensifications (I) and reductions (R) in the detected processes are also indicated. In the present state (1958–2001) shown in Fig. 11, some discrepancies are found with respect to Fig. 2. The results of the present study show more alternative areas of accretion/erosion in the mid-northern part, and the erosion in the mid-southern part is more pronounced. In addition, very local accretion found by the EUROSION project is not always correctly placed in our results (e.g. in the Costa Daurada area), although these differences are reasonable considering the methodology and the different spatial scales employed in the two works (coarser here than in the EUROSION study). For example, the higher percentage of cliffs areas in the northern part of the studied coast may be related with the incoherences found there since in the LST calculation we just considered a sandy coast without transversal limits. Moreover, different time spans were used to construct the pictures, and as a consequence the wave climates might be different. However, processes in some areas (e.g. erosion around Barcelona and accretion in the northernmost part of the domain) are well detected.
The extrapolation up to 2050 shows some changes in the classification of the stretches although a major general change is not detected. Analysing in more detail the behaviour of the different stretches, we observe that six of them maintain the same trend of beach evolution: three erosive and three accretive. Another nine stretches follow the same trend but with a different intensity. Keeping in mind the usual scarcity of—and high demand for—beach sediment on the Catalan coast (for both protection and leisure purposes), we consider that an accretive beach is optimal. Therefore, coming back to Fig. 11, we can say that six stretches will tend to behave “better” (less erosion or more accretion) and three “worse” (more erosion or less accretion). The beach evolution trend “improves” in four of the remaining stretches and “worsens” in five of them. Note that the accretion pattern in the southern part is shifted northwards in the future extrapolation which might be related with the increase of southerly events.
Therefore, according to the 2050 wave climate extrapolations and the employed methodology and taking into account the stretches’ length, 26 % of the Catalan coast would maintain the same beach evolution trend, 31 % would behave worse and 43 % would see an improved trend. This means that these future extrapolations indicate that more than 70 % of the Catalan coast could be affected by changes in wave climate and in particular in wave direction, and that their dynamics could be modified. Of these affected beaches, the evolution trend would worsen for 42 % and improve for 58 %. However, as the change in Q annual is not statistically significant, nor is the change in beach evolution.
5.3 Impact on harbour agitation
As explained in Section 3.3, the wave roses of nodes 14, 20 and 30 are used to calculate the propagation of the wave climate inside the ports of Blanes, Fòrum and Tarragona, respectively (see Fig. 1). Figure 12 shows the results of the mean agitation coefficient k a for each considered approaching direction and as a function of the H s entering the port (H s,ext ). For each of the ports, the entering wave directions that produce the most agitation are, in descending order, SW (only for Tarragona), S, SE and E. This is reasonable, considering the S-SW configuration of the harbour entrances. The degree of this dependency is not consistent, however, from one port to the next. The overall agitation in the Tarragona port seems the most direction-dependent because it has the highest k a (for SW waves) and also the lowest k a (for E waves). Fòrum has the lowest range for this coefficient and, in terms of agitation, it thus seems to have the best configuration to adapt to possible changes in wave direction. As a function of H s,ext , k a is found to be higher for the group of lowest wave height, except for the SW waves entering the Tarragona harbour. This coefficient decreases with H s,ext and tends to stabilise. This is as expected, since lower waves have shorter periods and as a consequence they are shorter and diffract less in the harbour entrance. Therefore, low waves are proportionally less damped than higher waves, which is not worrying as we are ultimately interested in the resulting wave height inside the port, H s,int rather than k a , which is the product of k a ·H s,ext . The increase in k a with H s,ext for SW waves entering the Tarragona port can only be explained by the generation of reflected waves. This is a bit worrying because in this case high values of k a and H s,ext coincide although very extreme waves coming from this direction are very improbable because of the fetch limitation caused by the Ebre delta.
Figures 13, 14 and 15 show, for each of the three ports, the wave heights obtained in two of the simulations (E and S directions with offshore H s,0 = 2.5 m). Agitation is clearly greater for waves coming from the south than for those coming from the east, in particular for the Tarragona and Blanes ports, which agrees with the previous results illustrated in Fig. 12. For E waves in Blanes (Fig. 13), the significant wave height H s inside the harbour, H s,int (x,y), is less than 40 cm—the maximum value recommended by the Spanish Port Authority in berths for leisure boats (Puertos del Estado 2000)—throughout almost the entire domain, reaching 50 cm at only a few points. In contrast, S waves penetrate the harbour more directly and H s,int (x,y) exceeds 40 cm at almost all points, reaching 1 m in some areas. At the Fòrum port (Fig. 14) the differences between the two cases are not as marked as at the other ports, with H s,int (x,y) values of less than 40 cm in many areas. The greatest differences are found in the areas surrounding the port entrance, where H s,int (x,y) can exceed 60 cm for S waves. Finally, in the Tarragona port (Fig. 15), the wave diffraction pattern is well marked in both cases. For E waves, H s,int (x,y) is less than 20 cm in large areas of the harbour and does not exceed 40 cm at any interior point. For S waves, H s,int (x,y) is less than 20 cm at only few points, while in many areas the wave height exceeds 40 cm, even reaching 80 cm in some places.
Table 1 summarises the effects of k a on the overall H s inside the port, \( \overline {{H_{{s,int}}}} \), for the present (1958–2001) and future (2050) scenarios computed using Eq. 14. The ratio between the two is included as well. The values in brackets are the 95 % confidence intervals that were calculated in the uncertainty analysis (see Section 4.4) by means of a bootstrapping technique with 1000 simulations. We want to point out that performing the trend analysis in terms of percentages and not in terms of H s or θ reduced drastically the computational cost as regarding to the confidence bounds estimation. For each bootstrapped sample, we did not have to simulate with the Boussinesq model the H s inside the harbour since the offshore H s to be propagated (representative of each interval \( \Delta {H_j} \) and \( \Delta {\theta_i} \)) was the same with the same direction, the only difference was the frequency of occurrence which only affected the linear combination of Eq. 14.
In absolute terms, the increase in the mean H s is small, but in relative terms the increase ranges from 11 % to 18 % and is always positive, since the lower bounds of the confidence intervals of these ratios are always greater than one. The uncertainty analysis also reveals that the increase can reach as high as 28 % for Blanes, 19 % for Fòrum and 21 % for Tarragona. These agitation increases could entail a decrease in the comfort and safety of the moored vessels as well as a reduction in the operability of the harbours, with the associated economic costs.
The wave climate extrapolation for 2050 and the numerical model results have shown that potential changes in wave direction patterns can have a considerable impact on harbour agitation. Although our analysis was limited to three harbours representative of different port types and geographic locations along the Catalan coast, the results can be extrapolated to most of the harbours in this region, because the entrances to 37 of the 47 harbours in Catalonia are oriented towards the southwest.
6 Conclusions
A 44-year (1958–2001) hindcast database was used to analyse trends in mean wave climate (wave height and direction) and to extrapolate future conditions on the Catalan coast (NW Mediterranean Sea). To perform this trend analysis a methodology was developed and applied to this data assuming that the trend estimated for 1958–2001 applies into the future. The extrapolated results for year 2050 indicated that the total amount of annual wave energy would remain practically constant with respect to the previous situation. More significant differences were observed in the distribution of frequencies among the various directions. In general, the frequency of waves was estimated to decrease from N and NE (which is in qualitatively agreement with the results of Najac et al. 2011) and increase from SE, S and SW. An uncertainty analysis was carried out using a bootstrapping technique. Although the uncertainty of the wave results was found to be considerable, the probability that some wave direction frequencies would change was estimated to be high. A similar tendency was obtained by Casas-Prat and Sierra (2010b) for extreme conditions but in the later case the uncertainty associated was considerably higher due to the reduction in the amount of data, in which just the evolution of wave direction and wave storminess associated to storm events was (separately) addressed.
The extrapolated future wave climate was used to predict the potential impacts on coastal dynamics and harbour agitation in the studied area. The net LST was assessed at different stretches along the Catalan coast. The methodology employed is simple, it has some limitations (simplification of the shoreline, use of a coarse spatial scale, different distances between the coast and the nodes where the wave climate is estimated, etc.) and further work is needed (use of a finer scale, better LST approach, etc. ). However, it was useful for illustrating possible changes in beach evolution trends due to variations in wave direction patterns. Our analysis found that net LST would tend to be lower and, in some cases, negative, meaning a net transport from S to N which is opposite to the main actual net LST. According to such variations, evolution trends would change at about 70 % of the analysed stretches, with 60 % of these changes being positive (i.e. the beach evolution trend would improve) and the other 40 % being negative. This apparent retreat of part of the coast is expected to be accompanied by reorientation of the coast since the changes in net LST are due to changes in wave directionality rather than wave height. Nevertheless, our uncertainty analysis did not find statistical significance in the computed LST changes which might be partly related to the current levels of uncertainty of the prediction of LST as pointed out by Sutherland and Gouldby (2003).
The extrapolated future wave climate was also used to analyse the possible impacts on harbour agitation. Three harbours, representative of different port types and geographic locations along the Catalan coast, were selected. A Boussinesq-type numerical model was used to estimate the penetration of waves inside the harbours. The results showed that in the extrapolated 2050 scenario agitation would increase by 11–18 % (or by as much as 19–28 %, taking into account the upper confidence bounds) in the three harbours, possibly reducing port operability and having an undetermined economic cost. These results could be extrapolated to most of the harbours in this region, because the entrances of 37 of the 47 ports in the area are oriented towards the southwest. For stormy conditions, Casas-Prat and Sierra (2010b) found a similar tendency towards higher agitation inside the Tarragona port. In the later case the expected increase was higher but more uncertain.
Another potential hazard (not studied here) related to changes in wave direction and associated variations in LST patterns is the possible increase in harbour siltation due to an increase in northward sediment transport and the large number of harbours with southward-oriented entrances. This could force harbours to enhance dredging operations, which would entail economic costs and decreased operability. A more detailed study in this sense would be necessary to assess this impact more accurately.
One main conclusion of this work is the need to take wave direction into account in studies of potential impacts of climate change in coastal areas as also pointed out by the recent study of Zacharioudaki and Reeve (2011) in the coastal management framework. Indeed, most studies on this topic only focused on the impact of sea-level rise or wave height alone. The results obtained herein are certainly limited to our assumptions and the use of hindcast data which do not explicitly account for the greenhouse effect and therefore it is advisable to compare our results with the wave projections obtained from projections of the atmosphere from climate models simulations, from which a similar impact assessment could be done. However, even if the future changes in wave direction are different from the ones predicted herein, this study makes clear that potential hazards associated with the wave direction (in this study: potential worse beach evolution trends and larger harbour agitation) must not be disregarded in the context of climate change.
References
Agresti A (2002) Categorical data analysis, 2nd edn. Wiley, New York, p 734
Aitchison J (1982) The statistical analysis of compositional data. J R Stat Soc Ser B 44(2):139–177
Alvarado-Aguilar D (2009) Coastal Flood Hazard Mapping at two scales. Application to the Ebro delta. Ph.D. thesis, Universitat Politècnica de Catalunya
Bayram A, Larson M, Hanson H (2007) A new formula for the total long-shore sediment transport rate. Coast Eng 54:700–710
Casas-Prat M, Sierra JP (2010a) Trend analysis of the wave storminess: the wave direction. Adv Geosci 26:89–92
Casas-Prat M, Sierra JP (2010b) Trend analysis of wave storminess: wave direction. Impact on harbour agitation. Nat Hazards Earth Syst Sci 10:2327–2340
Cazenave A, Nerem RS (2004) Present-day sea level change: observations and causes. Rev Geophys 42:RG3001
CERC (1984) Shore Protection Manual. Coastal Engineering Research Center, Department of the Army, U.S. Corps of Engineers, Washington, DC
Coelho C, Silva R, Veloso-Gomes F, Taveira-Pinto F (2009) Potential effects of climate change on northwest Portuguese coastal zones. J Mar Sci 66(7):1497–1507
Criado-Aldeanueva F, Vera JDR, Garcia-Lafuente J (2008) Steric mass-induced Mediterranean sea level trends from 14 years of altimetry data. Glob Planet Change 60(3–4):563–575
Dickson ME, Walkden MJA, Hall JW (2007) Systematic impacts of climate change on an eroding coastal region over the twenty-first century. Clim Change 84:141–166
Egozcue JJ, Pawlowsky-Glahn V, Mateu-Figueras G, Barceló-Vidal C (2003) Isometric logratio transformations for compositional data analysis. Math Geol 35:279–300
González-Marco D, Sierra JP, Fernández de Ybarra O, Sánchez-Arcilla A (2008) Implications of long waves in harbor Management: The Gijon port case study. Ocean Coast Manag 51:180–201
Grabemann I, Weisse R (2008) Climate change impact on extreme wave conditions in the North Sea: an ensemble study. Ocean Dynam 58:199–212
Guedes Soares C, Carretero-Albiach JC, Weisse R, Alvarez-Fanjul E (2002) A 40 years hindcast of wind, sea level and waves in European waters. Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering, Oslo, Norway, pp. 669–675
Hallermeier RJ (1978) Uses for a Calculated Limit Depth to Beach Erosion. Proceedings of the 16th Conference on Coastal Engineering, Hamburg, Germany, pp. 1493–1512
Hemer MA (2009) Identifying coasts susceptible to wave climate change. J Coast Res SI 56:228–232
Hemer MA, McInnes K, Church JA, O’Grady J, Hunter JR (2008) Variability and trends in the Autstralian wave climate and consequent coastal vulnerability. CSIRO: Final Report for Department of Climate Change Surface Ocean Wave Variability Project, pp. 120
Inman, DL, Bagnold RA (1963) In: Hill MN (ed) Littoral processes, in the Sea, vol 3. Interscience, New York, pp. 529–533
Jiménez JA, Madsen OS (2003) A simple formula to estimate settling velocity of natural sediments. J Waterw Port C-ASCE 129:70–78
Kamphuis JW (1991) Along-shore sediment transport rate. J Waterw Port C-ASCE 177:624–641
Kamphuis JW (2002) A sediment pickup rate formula based on energy dissipation rate by random breaking waves. Proceedings of the 28th International Conference on Coastal Engineering, Cardiff, UK, pp. 2859–2872
King DB (2005) Influence of grain size on sediment transport rates with emphasis on the total long-shore rate. US Army Corps, 2005
Lionello P, Cogo S, Galati MB, Sanna A (2008) The Mediterranean surface wave climate inferred from future scenario simulations. Glob Planet Change 63:152–162
Lowe JA, Gregory JM, Flather RA (2001) Changes in the occurrence of storm surges in the United Kingdom under a future climate scenario using a dynamic storm surge model driven by the Hadley Center climate models. Clim Dynam 18:179–188
Mestres M, Sierra JP, Mösso C, Sánchez-Arcilla A (2010) Sources of contamination and modelled pollutant trajectories in a Mediterranean harbour (Tarragona, Spain). Mar Pollut Bull 60:898–907
Mousavi ME, Irush JL, Frey AE, Olivera F, Edge BL (2011) Global warming and hurricanes: the potencial impact of hurricane intensification and sea level rise on coastal flooding. Clim Change 104:575–597
Munk WH (2002) Twentieth century sea level: an enigma. Proc Nat Acad Sci 99(10):6550–6555
Musić S, Nicković S (2008) 44-year wave hindcast for the Eastern Mediterranean. Coast Eng 55:872–880
Najac J, Lac C, Terray L (2011) Impact of climate change on surface winds in France using a statistical-dynamical downscaling method with mesoscale modelling. Int J Climatol 31:415–430
Pawlowsky-Glahn V, Egozcue JJ (2006) Compositional data and their analysis: an introduction (in compositional data analysis in the geosciences; from theory to practice). Geol Soc Lond Spec Publ 264:1–10
Puertos del Estado (1992) ROM 0.3-91. Oleaje. Anejo I. Clima Marítimo en el Litoral Español (in Spanish). Technical report. Ministerio de Obras Públicas y Transportes, Madrid (Spain)
Puertos del Estado (2000) ROM 3.1-99 Proyecto de la Configuración Marítima de los Puertos, canales de acceso y areas de flotación (in Spanish). Technical report. Ministerio de Fomento, Madrid (Spain)
Ratsimandresy AW, Sotillo MG, Carretero JC, Álvarez-Fanjul E, Haiji H (2008) A 44-year high resolution ocean and atmospheric hindcast for the Mediterranean Basin developed within the HIPOCAS project. Coast Eng 55:827–842
Sánchez-Arcilla A, Jiménez JA, Valdemoro HI, Gracia V, Sole F, Ariza E, Mendoza ET (2007) Estat de la zona costanera a Catalunya (in Catalan). Technical report. Centre Internacional d’Investigació dels Recursos Costaners, pp. 351
Sánchez-Arcilla A, González-Marco D, Bolaños R (2008) A review of wave climate and prediction along the Spanish Mediterranean coast. Nat Hazards Earth Syst Sci 8:1217–1228
Sánchez-Arcilla A, Mósso C, Sierra JP, Mestres M, Harzallah A, Senouci M, El Raey M (2010) Climate drivers of potencial hazards in Mediterranean coasts. Reg Environ Change 11(3):617–636
Sole F, Gracia V, Valdemoro, HI, Mendoza, ET, Jiménez, JA, Sánchez-Arcilla, A (2010) Variations in sediment textural parameters along the Catalan coast. Natural vs human factors. 27th meeting of the International Association of Sedimentologists, Alghero, Italy, September 2009
Sotillo MG, Ratsimandresy AW, Carretero JC, Bentamy A, Valero F, González-Rouco F (2005) A high resolution 44-year atmospheric hindcast for the Mediterranean Basin: contribution to the regional improvement to global reanalysis. Clim Dynam 25:219–236
Sutherland J, Gouldby B (2003) Vulnerability of coastal defences to climate change. Water Mar Eng 156(WM2):137–145
Wang XL, Swail VR (2001) Changes of extreme wave heights in Northern Hemisphere oceans and related atmospheric circulation regimes. J Climate 14(10):2204–2221
Wang XL, Swail VR (2002) Trends of Atlantic wave extremes as simulated in a 40-yr wave hindcast using kinematically reanalyzed wind fields. J Climate 15(9):1020–1035
Wang XL, Swail VR (2006) Climate change signal and uncertainty in projections of ocean wave heights. Clim Dynam 26:109–126
Wang XL, Zwiers FW, Swail VR (2004) North Atlantic Ocean wave climate change scenarios for the twenty-first century. J Climate 17:2368–2383
Wang XL, Swail VR, Cox A (2010) Dynamical versus statistical downscaling methods for ocean wave heights. Int J Climatol 30:317–332
Weisse R, von Storch H (2010) Marine climate and climate change. Storms, wind waves and storm surges. Springer, Praxis Publishing, Chichester, UK
Zacharioudaki A, Reeve DE (2011) Shoreline evolution under climate change wave scenarios. Clim Change 108(1–2):73–105
Acknowledgments
This research was carried out in the frame of the European project “Climate Change and Impact Research: The Mediterranean Environment (CIRCE)” (contract number TST5-CT-2007-036961) and the Spanish project “Vulnerabilidad, impactos y adaptación al cambio climático: estudio integrado sobre la agricultura, recursos hídricos y costas (ARCO)” (contract number 200800050084350). We are grateful to the Organismo Público Puertos del Estado (Spanish National Ports and Harbours Authority) for providing HIPOCAS data. The first author was firstly supported by an UPC PhD grant and is currently enjoying a PhD grant from the Ministerio de Educación (Spanish Ministry of Education). She also acknowledges the support received by the Col·legi d’Enginyers de Camins, Canals i Ports – Catalunya (Civil Engineering Association in Catalonia).
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Casas-Prat, M., Sierra, J.P. Trend analysis of wave direction and associated impacts on the Catalan coast. Climatic Change 115, 667–691 (2012). https://doi.org/10.1007/s10584-012-0466-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-012-0466-9