Abstract
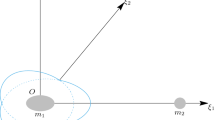
A family of periodic orbits is proven to exist in the spatial lunar problem that are continuations of a family of consecutive collision orbits, perpendicular to the primary orbit plane. This family emanates from all but two energy values. The orbits are numerically explored. The global properties and geometry of the family are studied.















Similar content being viewed by others
Notes
It is noted that there are two consecutive collision orbits, one on the positive \(\hat{q}_3\)-axis and the other on the negative \(\hat{q}_3\)-axis. We just consider the orbit on the positive axis, without loss of generality.
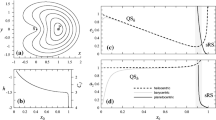
A quick overview of the terminology: by elliptic we mean two conjugate eigenvalues on the unit circle. This implies a weak form of stability: nearby orbits cannot escape quickly. By hyperbolic we mean two real eigenvalues: \(\lambda \) and \(1/\lambda \). We add “negative” to indicate that \(\lambda <0\). The return map in the spatial problem has four eigenvalues, satisfying the symmetry property: if \(\lambda \) is an eigenvalue, then so are \(\bar{\lambda }\), \(1/\lambda \) and \(1/\bar{\lambda }\). This leaves one additional case in this dimension, namely none of the eigenvalues are purely real, nor do they lie on the unit circle: we will call this complex hyperbolic. All forms of hyperbolicity imply instability in the sense that nearby orbits tend to escape quickly: how quickly depends on the absolute value of the largest eigenvalue.
We remind the reader that the critical energy for \(\mu =0.5\) equals \(-2.0\).
References
Albers, P., Frauenfelder, U., van Koert, O., Paternain, G.: Contact geometry of the restricted three-body problem. Commun. Pure Appl. Math. 65, 229–263 (2012)
Belbruno, E.: A new regularization of the restricted three-body problem and an application. Celest. Mech. Dyn. Astron. 25, 397–415 (1981)
Belbruno, E.: A new family of periodic orbits for the restricted problem. Celest. Mech. Dyn. Astron. 25, 195–217 (1981)
Belbruno, E., Frauenfelder, U., van Koert, O.: The \(\varOmega \)-limit set of a family of chords. arXiv:1811.09213 (2018)
CAPD-computer assisted proofs in dynamics, a package for rigorous numerics, http://capd.ii.uj.edu.pl/ Accessed 22 Oct 2018
Cho, W., Kim, G.: The circular spatial restricted 3-body problem. arXiv:1810.05796 (2018)
Frauenfelder, C., van Koert, O.: The Restricted Three-Body Problem and Holomorphic Curves. Pathways in Mathematics. Springer, Berlin (2018)
Hill, G. W.: Researches in the lunar theory. Am. J. Math. 1, 5–27, 129–148, 245–251 (1878)
Jorba, A., Zou, M.: A software package for the numerical integration of ODEs by means of high-order Taylor methods. Exp. Math. 14, 99–117 (2005)
Kapela, T., Simó, C.: Computer assisted proofs for nonsymmetric planar choreographies and for stability of the Eight. Nonlinearity 20, 1241–1255 (2007)
Kummer, M.: On the stability of Hill’s solutions in the plane restricted three body problem. Am. J. Math. 101, 1333–1354 (1979)
Kummer, M.: On the three-dimensional lunar problem and other perturbation problems of the Kepler problem. J. Math. Anal. Appl. 93, 142–194 (1983)
Meyer, K., Hall, G., Offin, D.: Introduction to Hamiltonian Dynamical Systems and the N-body Problem. Applied Mathematical Sciences 90, Springer, New York, (2009)
Yanguas, P., Palacian, F., Meyer, K., Dumas, H.: Periodic solutions in Hamiltonians, averaging, and the lunar problem. SIAM J. Appl. Dyn. Sys. 7, 311–340 (2008)
Rabinowitz, P.: Periodic solutions of Hamiltonian systems. Commun. Pure Appl. Math. 31, 157–184 (1978)
Schmidt, D.: Families of periodic orbits in the restricted problem of three bodies connecting families of direct and retrograde orbits. SIAM J. Appl. Math. 22, 27–37 (1972)
Siegel, C.L., Moser, J.K.: Lectures on Celestial Mechanics. Springer, Berlin (1971)
Wilczak, D., Zgliczyński, P.: Period doubling in the Rossler system—a computer assisted proof. Foundations Comput. Math. 9, 611–649 (2009)
Acknowledgements
Edward Belbruno would like to acknowledge the support of Humboldt Stiftung of the Federal Republic of Germany that made this research possible and the support of the University of Augsburg for his visit from 2018-19. Research by E.B. was partially supported by NSF grant DMS-1814543. Urs Frauenfelder was supported by DFG grant FR 2637/2-1, of the German government. Otto van Koert was supported by NRF grant NRF-2016R1C1B2007662, funded by the Korean Government.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors state that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix: Regularization in coordinates
Moser regularization is based on \(n-\)dimensional stereographic projection. The position and momentum variables are given by \(q = (q_1, q_2, \ldots , q_n) \in \mathbb {R}^n\) , \(p = (p_1, p_2, \ldots , p_n) \in \mathbb {R}^n\). We denote by \((q,p) \in T^*\mathbb {R}^n\) a point in the (co)-tangent bundle of \(\mathbb {R}^n\), where we think of \(\mathbb {R}^n\) as a chart for \(S^n = \{|\xi |^2 = \varSigma _{i=0}^{n} \xi _i^2 = 1\}\), \(\xi = (\xi _0, \xi _1, \ldots , \xi _n)\). We set \(x= - p\) and \(y=q\), and define the (co)-tangent bundle of \(S^n\) as
To go from \(T^*S^n\) to \(T^*\mathbb {R}^n\) we use the map
where \(\tilde{\xi } = (\xi _1, \xi _2, \ldots , \xi _n)\). Collision corresponds to \(\xi _0 = 1\).
To go from \(T^*\mathbb {R}^n\) to \(T^*S^n\), we use the inverse given by
The Belbruno transform employs a Möbius transformation which sends to the collision point \(|p| = \infty \) to \(P=(1,0,\ldots ,0)\in \mathbb {R}^n\). In coordinates for three dimensions (the index \(j=2,3\)), the forward Belbruno transformation is given by
The inverse Belbruno transform is given by
Appendix: Hamiltonian vector field with constraints
The setup is the following. We are given a manifold M, which is a symplectic submanifold of the symplectic manifold \((N,\varOmega )\). We denote the inclusion by \(\iota : M\rightarrow N\), and the induced symplectic form on M by \(\omega :=\iota ^*\varOmega \). We assume that \(M=f_1^{-1}(0) \cap f_2^{-1}(0)\). In addition, we are given a Hamiltonian function \(H_N:N \rightarrow \mathbb {R}\), and we have the induced Hamiltonian \(H_M=\iota ^*H_N\). In our case \(N=T^*\mathbb {R}^{n+1}\) and \(M:=T^*S^n\).
The functions that define M are
In our case, the symplectic manifold \(N=T^*\mathbb {R}^{n+1}\) has a global chart, but \(T^*S^n\) has not. We will give a formula for the Hamiltonian vector field \(X_H\) on M in terms of Hamiltonian vector field on N. In our example, this means that we can use the global coordinates on \(N=T^*\mathbb {R}^{n+1}\). We have
where
The Poisson brackets defined by \(\{ f, g\}:=\omega (X_f, X_g\}\) are of course not needed to do the computations, but they clarify the situation if M is a symplectic submanifold of higher codimension, where a matrix filled with \(\{ f_i, f_j \}\) has to be inverted. A computation shows that the above vector field is tangent to the submanifold M and that it is the Hamiltonian vector field.
Rights and permissions
About this article
Cite this article
Belbruno, E., Frauenfelder, U. & van Koert, O. A family of periodic orbits in the three-dimensional lunar problem. Celest Mech Dyn Astr 131, 7 (2019). https://doi.org/10.1007/s10569-019-9882-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10569-019-9882-8