Bioeconomic management of invasive vector-borne diseases

Abstract

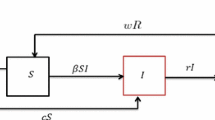
Invasive insects, arthropods, and other invertebrates are of concern due to the role some play in introducing and transmitting pathogens via a pathogen–vector relationship. Indeed, vector-borne diseases represent a significant portion of emerging diseases. We compare and contrast three strategic approaches to managing a vector-borne pathogen: conventional strategies based on disease ecology without regard to economic tradeoffs and cost-effective strategies based on a bioeconomic framework. Conventional strategies entail managing the vector population below a threshold value based on R ₀—the basic reproductive ratio of the pathogen, which measures a pathogen’s ability to invade uninfected systems. This does not account for post-infection dynamics, nor does it balance ecological and economic tradeoffs. Thresholds take on a more profound role under a bioeconomic paradigm: rather than unilaterally determining vector control choices, thresholds inform control choices and are influenced by them. Simulation results show cost-effective strategies can lower overall program costs and may be less sensitive to parameter estimation.

Appendix

(A) Derivation of condition (7)

Upon imposing the requirement that h _i  < 1, condition (6) indicates that

$$ 1 > \beta_{wi} \theta_{w} /\theta_{i} - (\beta_{wi} \theta_{w} + \delta_{i} ) = \beta_{wi} \theta_{w} (1/\theta_{i} - 1) - \delta_{i} . $$

(A1)

Condition (A1) can be re-written as

$$ \delta_{i} + 1 > \beta_{wi} \theta_{w} (1/\theta_{i} - 1) = \beta_{wi} \theta_{w} (N_{i} /I_{i} - I_{i} /I_{i} ) = \beta_{wi} \theta_{w} (S_{i} /I_{i} ). $$

(A2)

Write $\theta_{w} = I_{w} /N_{w}$ and solve for S _i :

$$ S_{i} < \left[ {\delta_{i} + 1} \right]{\frac{{I_{i} N_{w} }}{{\beta_{wi} I_{w} }}} = \left[ {\delta_{i} + 1} \right]{\frac{{\alpha_{w} K_{w} }}{{\beta_{iw} \beta_{wi} }}}{\frac{{I_{i} }}{{I_{w} }}}{\frac{{N_{w} }}{{K_{w} }}}{\frac{{\beta_{iw} }}{{\alpha_{w} }}}, $$

(A3)

where the last equality simply comes from multiplying both the numerator and the denominator by $\alpha_{w} K_{w} \beta_{iw}$. Upon applying the distributive property, condition (A3) becomes

$$ S_{i} < \left[ {{\frac{{\alpha_{w} \delta_{i} K_{w} }}{{\beta_{iw} \beta_{wi} }}} + {\frac{{\alpha_{w} K_{w} }}{{\beta_{iw} \beta_{wi} }}}} \right]{\frac{{I_{i} }}{{I_{w} }}}{\frac{{N_{w} }}{{K_{w} }}}{\frac{{\beta_{iw} }}{{\alpha_{w} }}} = \left[ {N_{Ti} + {\frac{{\alpha_{w} K_{w} }}{{\beta_{iw} \beta_{wi} }}}} \right]{\frac{{I_{i} }}{{I_{w} }}}{\frac{{N_{w} }}{{K_{w} }}}{\frac{{\beta_{iw} }}{{\alpha_{w} }}}, $$

(A4)

which is condition (7).

(B) Optimal vector management

Problem (12) can be formulated as a linear control problem (i.e., the problem is linear in the control variable y _i ). The Hamiltonian for the problem is:

$$ H = - {\frac{{cy_{i}^{{}} }}{{N_{i} }}} + \lambda_{w} \dot{S}_{w} + \mu_{w} \dot{I}_{w} + \lambda_{i} \dot{S}_{i} + \mu_{i} \dot{I}_{i} , $$

(B1)

where $\lambda_{j}$ is the co-state variable associated with the susceptible stock of population j, and $\mu_{j}$ is the co-state variable associated with the infected stock of population j (j = w,i).The marginal value of y _i on the Hamiltonian is:

$$ {\frac{\partial H}{{\partial y_{i} }}} = - {\frac{c}{{N_{i} }}} - \lambda_{i} {\frac{{S_{i} }}{{N_{i} }}} - \mu_{i} {\frac{{I_{i} }}{{N_{i} }}} $$

(B2)

The marginal value in (B2) vanishes along a singular path. When the value is positive (negative), then h _i should be set at its maximum (minimum) value. Generally, the system will not be on the singular path initially, which means an extremal control must be used to move the system as quickly as possible to the singular path (if one exists) (Clark 2005). As there is no upper bound on y _i , harvests can only occur at a maximum rate for an instant. Harvests can persist at y _i  = 0 or at the singular level for a longer time. Hence, except for an initial jump, we have

$$ y_{i} = \dot{y}_{i} = 0,\,{\text{or}}\quad \partial H/\partial y_{i} = 0. $$

(B3)

The remaining necessary conditions for problem (12) are:

$$ \dot{\lambda }_{w} = - {\frac{\partial H}{{\partial S_{w} }}} $$

(B4)

$$ \dot{\mu }_{w} = - {\frac{\partial H}{{\partial I_{w} }}} $$

(B5)

$$ \dot{\lambda }_{i} = - {\frac{\partial H}{{\partial S_{i} }}} $$

(B6)

$$ \dot{\mu }_{i} = - {\frac{\partial H}{{\partial I_{i} }}} $$

(B7)

The transversality conditions are:

$$ \lambda_{w} (\tau ) = {\frac{\partial V}{{\partial S_{w} }}} > 0 $$

(B8)

$$ \mu_{w} (\tau ) = 0 $$

(B9)

$$ \lambda_{i} (\tau ) = 0 $$

(B10)

$$ \mu_{i} (\tau ) = 0 $$

(B11)

Conditions (B10) and (B11), along with (B2), indicates that h _i (τ) = 0. Taking the time derivative of the Hamiltonian yields:

$$ \begin{aligned} {\frac{\partial H}{\partial t}} & = {\frac{\partial H}{{\partial y_{i} }}}\dot{y}_{i} + \sum\limits_{j = w,i} {\left[ {{\frac{\partial H}{{\partial S_{j} }}}\dot{S}_{j} + {\frac{\partial H}{{\partial I_{j} }}}\dot{I}_{j} + {\frac{\partial H}{{\partial \lambda_{j} }}}\dot{\lambda }_{j} + {\frac{\partial H}{{\partial \mu_{j} }}}\dot{\mu }_{j} } \right]} \\ {\frac{\partial H}{\partial t}} & = 0 + \sum\limits_{j = w,i} {\left[ {{\frac{\partial H}{{\partial S_{j} }}}\dot{S}_{j} + {\frac{\partial H}{{\partial I_{j} }}}\dot{I}_{j} + \dot{S}_{j} \dot{\lambda }_{j} + \dot{I}_{j} \dot{\mu }_{j} } \right]} \\ {\frac{\partial H}{\partial t}} & = 0 + \sum\limits_{j = w,i} {\left[ {{\frac{\partial H}{{\partial S_{j} }}}\dot{S}_{j} + {\frac{\partial H}{{\partial I_{j} }}}\dot{I}_{j} + \dot{S}_{j} \left( { - {\frac{\partial H}{{\partial S_{j} }}}} \right) + \dot{I}_{j} \left( { - {\frac{\partial H}{{\partial I_{j} }}}} \right)} \right]} = 0. \\ \end{aligned} $$

(B12)

The second row of (B12) comes from condition (B3), while the third row comes from conditions (B4)–(B11). Hence, H is constant after possibly an initial pulse harvest. Define this constant value of H by χ, i.e., H = χ. Using the results H = χ and h _i (τ) = 0, along with the transversality conditions (B8)–(B11), we have

$$ H(\tau ) = 0 + \lambda_{w} (\tau )\dot{S}_{w} (\tau ) = - {\frac{\partial V}{{\partial S_{w} (\tau )}}}\beta_{iw} I_{i} (\tau ){\frac{{S_{w} (\tau )}}{{N_{w} (\tau )}}} = \chi < 0, $$

(B13)

which means H(t) < 0 for all t ∈ [0, τ).

As H is a measure of economic welfare, the result H(τ) < 0 means that extending the time horizon to τ reduces welfare. It would be optimal to diminish the time horizon to some value $\tau^{\prime} < \tau$, such that $H(\tau^{\prime}) = 0$, as setting $H(\tau^{\prime}) = 0$ means there is no value to extending the time horizon any further (Clark 2005). However, this is not possible since τ is biologically-determined and is therefore exogenously fixed. The implication is that it is optimal to take all actions as soon as possible: an impulse control at time t = 0. The intuition is as follows. First, there is no incentive to delay management because problem (12) is a linear control problem with no discounting. If discounting occurred at a very high rate, then future costs (and benefits) would be worth less and so one would want to wait to invest in vector controls. With no discounting, costs today and in the future are valued equally, so there is no penalty from investing early. But there is a penalty to investing later, as the only stock of concern, S _w , can only decrease when the disease problem gets worse. So it is optimal for all vector reduction to take place immediately. The cost associated with an impulse control used for the initial cull is $c\ln [N_{i0} /(N_{i0} - y_{i} (0))]$ (Clark 2005).To determine the optimal initial harvest, rewrite the problem as

$$ \begin{array}{*{20}c} {\mathop {\text{Max}}\limits_{{y_{i} (0)}} } & { - c\ln \left[ {{\frac{{N_{i0} }}{{N_{i0} - y_{i} (0)}}}} \right] + V(S_{w} (\tau ))} \\ \end{array} $$

(B14)

subject to the equations of motion and the initial conditions as before, except that now we have the following initial conditions for the vector populations: $S_{i} (0^{ + } ) = S_{i0} (1 - y_{i} (0)/N_{i0} )$ and $I_{i} (0^{ + } ) = I_{i0} (1 - y_{i} (0)/N_{i0} )$. The objective function in (B14) now does not depend on time, and the equations of motion no longer depend on human choices. We solve the equations of motion (1)–(4) as functions of the stock levels after the initial cull, and then rewrite problem (B14) as

$$ \begin{array}{*{20}c} {\mathop {\text{Max}}\limits_{{y_{i} (0)}} } & { - c\ln \left[ {{\frac{{N_{i0}^{{}} }}{{N_{i0}^{{}} - y_{i}^{{}} (0)}}}} \right] + V(S_{w} (\tau ,S_{w0} ,I_{w0} ,S_{i0} [1 - y_{i} (0)/N_{i0} ],I_{i0} [1 - y_{i} (0)/N_{i0} ]))} \\ \end{array} , $$

(B15)

or, more simply, as

$$ \begin{array}{*{20}c} {\mathop {\text{Max}}\limits_{{h_{i} (0)}} } & { - c\ln \left[ {{\frac{1}{{(1 - h_{i}^{{}} (0))}}}} \right] + V(S_{w} (\tau ,S_{w0} ,I_{w0} ,S_{i0} [1 - h_{i} (0)],I_{i0} [1 - h_{i} (0)]))} \\ \end{array} $$

(B16)

The optimality condition for this problem is:

$$ {\frac{c}{{(1 - h_{i}^{{}} (0))}}} = {\frac{{\partial V\left( {S_{w} \left( \tau \right)} \right)}}{{\partial S_{w} }}}\left[ { - {\frac{{\partial S_{w} }}{{\partial S_{i} (0^{ + } )}}}S_{i0} - {\frac{{\partial S_{w} }}{{\partial I_{i} (0^{ + } )}}}I_{i0} } \right] $$

(B17)

The left hand side of (B17) is the marginal cost of vector controls. Marginal costs approach infinity as the harvest rate $h_{i} (0)$ approaches unity; hence it is not optimal to eradicate the vector population assuming the marginal benefits of eradication are finite. The right hand side is the marginal net benefit of vector controls in time period 0. Society benefits from a larger value of $S_{w} (\tau )$. This value is increased at the margin as $I_{i} (0^{ + } )$ is reduced (i.e., $- \partial S_{w} /\partial I_{i} (0^{ + } ) > 0$), and it may increase or decrease as $S_{i} (0^{ + } )$ is reduced (i.e., $- \partial S_{w} /\partial S_{i} (0^{ + } )_{ < }^{ \ge } 0$).

It is worth noting that the impacts of the initial cull will depend on the time horizon τ. The smaller is τ, the larger the impact of a given initial cull on $S_{w} (\tau )$, as the vector population will have less time to rebound and infect the host population. In contrast, a larger τ gives infected vectors more time to rebound and infect hosts after the initial cull. Our numerical sensitivity analysis indicates that the less control is required when τ is small, as having only few controls can yield effective protection of the host population in this case while keeping costs low. The optimal level of vector controls is initially increasing in τ, as vector control efforts are initially substituted for reduced protection effectiveness as τ is increased. If τ is too large, however, the level of control is reduced in response to reduced effectiveness; more hosts become infected while society saves from reduced control costs.