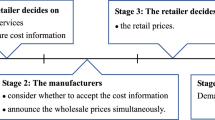
Abstract
This paper investigates the effects of reselling and agency contracts on the platform’s incentive to share information under two scenarios, i.e., the recommendation scenario and non-recommendation scenario. Through analyzing the equilibrium solutions, we derive the following results. First, comparing the recommendation and non-recommendation scenarios, the platform prefers the recommendation scenario under the reselling contract. However, contrary to traditional wisdom, when the recommendation efficiency is relatively more efficient, the platform chooses the non-recommendation scenario in the agency contract; as the recommendation efficiency becomes less efficient, the recommendation scenario is preferred in the agency contract. Second, for the reselling contract, the platform prefers to withhold demand information in the recommendation and non-recommendation scenarios. However, the platform voluntarily shares this information under the agency contract for the two scenarios. Third, the platform’s optimal strategy depends on the commission rate, the platform’s recommendation efficiency, and the level of information accuracy. Intuitively, a lower commission rate induces the platform to prefer the reselling contract in the recommendation and non-recommendation scenarios. However, a higher commission rate does not always make the platform choose the agency contract. The recommendation efficiency and the level of information accuracy affect the platform’s optimal strategy. Furthermore, given the platform’s optimal strategy, there are Pareto optimal regions that make the manufacturer better off. That is, the platform and the manufacturer achieve a win–win situation. Finally, in an extension of the model, this paper shows the platform’s optimal strategy when a hybrid contract is used, which also demonstrates the robustness of the results.








Similar content being viewed by others
References
Abhishek, V., Jerath, K., & Zhang, Z. J. (2016). Agency selling or reselling? Channel structures in electronic retailing. Management Science, 62(8), 2259–2280.
Adomavicius, G., Bockstedt, J. C., Curley, S. P., & Zhang, J. J. (2018). Effects of online recommendations on consumers’ willingness to pay. Information Systems Research, 29(1), 84–102.
Ai, X. Z., Chen, J., & Ma, J. H. (2012). Contracting with demand uncertainty under supply chain competition. Annals of Operations Research, 201(1), 17–38.
Bian, W., Shang, J., & Zhang, J. (2016). Two-way information sharing under supply chain competition. International Journal of Production Economics, 178, 82–94.
Chen, L., Nan, G., & Li, M. (2018). Wholesale pricing or agency pricing on online retail platforms: The effects of customer loyalty. International Journal of Electronic Commerce, 22(4), 576–608.
Choi, T. M., Li, J., & Wei, Y. (2013). Will a supplier benefit from sharing good information with a retailer? Decision Support Systems, 56, 131–139.
Chu, L. Y., Shamir, N., & Shin, H. (2017). Strategic communication for capacity alignment with pricing in a supply chain. Management Science, 63(12), 4366–4388.
De, P., Hu, Y., & Rahman, M. S. (2010). Technology usage and online sales: An empirical study. Management Science, 56(11), 1930–1945.
Dong, C., Yang, Y., & Zhao, M. (2018). Dynamic selling strategy for a firm under asymmetric information: Direct selling vs. Agent selling. International Journal of Production Economics, 204, 204–213.
Fawcett, S. E., Wallin, C., Allred, C., Fawcett, A. M., & Magnan, G. M. (2011). Information technology as an enabler of supply chain collaboration: A dynamic-capabilities perspective. Journal of Supply Chain Management, 47(1), 38–59.
Geng, X. J., Tan, Y. L., & Wei, L. (2018). How add-on pricing interacts with distribution contracts. Production and Operations Management, 27(4), 605–623.
Ghoshal, A., Kumar, S., & Mookerjee, V. (2015). Impact of recommender system on competition between personalizing and non-personalizing firms. Journal of Management Information Systems, 31(4), 243–277.
Guo, L. (2009). The benefits of downstream information acquisition. Marketing Science, 28(3), 457–471.
Ha, A. Y., Tian, Q., & Tong, S. L. (2017). Information sharing in competing supply chains with production cost reduction. M&Som-Manufacturing & Service Operations Management, 19(2), 246–262.
Ha, A. Y., & Tong, S. (2008). Contracting and information sharing under supply chain competition. Management Science, 54(4), 701–715.
Ha, A. Y., Tong, S., & Zhang, H. (2011). Sharing demand information in competing supply chains with production diseconomies. Management Science, 57(3), 566–581.
Hao, L., & Tan, Y. (2019). Who wants consumers to be informed? Facilitating information disclosure in a distribution channel. Information Systems Research, 30(1), 34–49.
Huang, S., Guan, X., & Chen, Y. J. (2018). Retailer information sharing with supplier encroachment. Production and Operations Management, 27(6), 1133–1147.
Kumar, A., & Hosanagar, K. (2019). Measuring the value of recommendation links on product demand. Information Systems Research, 30(3), 819–838.
Li, B., Zhu, M., Jiang, Y., & Li, Z. (2016). Pricing policies of a competitive dual-channel green supply chain. Journal of Cleaner Production, 112, 2029–2042.
Li, C., Chu, M., Zhou, C., & Xie, W. (2019a). Is it always advantageous to add-on item recommendation service with a contingent free shipping policy in platform retailing? Electronic Commerce Research and Applications, 37, 1–11.
Li, L., Chen, J., & Raghunathan, S. (2018). Recommender system rethink: Implications for an electronic marketplace with competing manufacturers. Information Systems Research, 29(4), 1003–1023.
Li, L., & Zhang, H. (2008). Confidentiality and information sharing in supply chain coordination. Management Science, 54(8), 1467–1481.
Li, L. D. (2002). Information sharing in a supply chain with horizontal competition. Management Science, 48(9), 1196–1212.
Li, X. J., Chen, J., & Ai, X. Z. (2019b). Contract design in a cross-sales supply chain with demand information asymmetry. European Journal of Operational Research, 275(3), 939–956.
Mishra, B. K., Raghunathan, S., & Yue, X. (2009). Demand forecast sharing in supply chains. Production and Operations Management, 18(2), 152–166.
Mukhopadhyay, S. K., Su, X. M., & Ghose, S. (2009). Motivating retail marketing effort: Optimal contract design. Production and Operations Management, 18(2), 197–211.
Pathak, B., Garfinkel, R., Gopal, R. D., Venkatesan, R., & Yin, F. (2010). Empirical analysis of the impact of recommender systems on sales. Journal of Management Information Systems, 27(2), 159–188.
Raju, J. S., & Roy, A. (2000). Market information and firm performance. Management Science, 46(8), 1075–1084.
Shang, W. X., Ha, A. Y., & Tong, S. (2016). Information sharing in a supply chain with a common retailer. Management Science, 62(1), 245–263.
Shen, Y. L., Willems, S. P., & Dai, Y. (2019). Channel selection and contracting in the presence of a retail platform. Production and Operations Management, 28(5), 1173–1185.
Tian, L., Vakharia, A. J., Tan, Y., & Xu, Y. (2018). Marketplace, reseller, or hybrid: Strategic analysis of an emerging e-commerce model. Production and Operations Management, 27(8), 1595–1610.
Wang, J., Huang, P., Zhao, H., Zhang, Z., Zhao, B., Lee, D. L., & Acm. (2018). Billion-scale commodity embedding for e-commerce recommendation in alibaba. In Kdd'18: Proceedings of the 24th ACM Sigkdd international conference on knowledge discovery & data mining (pp. 839–848).
Wu, H., Cai, G., Chen, J., & Sheu, C. (2015). Online manufacturer referral to heterogeneous retailers. Production and Operations Management, 24(11), 1768–1782.
Xu, G. Y., Dan, B., Zhang, X. M., & Liu, C. (2014). Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract. International Journal of Production Economics, 147, 171–179.
Xue, W. L., Zuo, J. J., & Xu, X. L. (2017). Analysis of market competition and information asymmetry on selling strategies. Annals of Operations Research, 257(1–2), 395–421.
Yan, R., & Pei, Z. (2015). Incentive information sharing in various market structures. Decision Support Systems, 76, 76–86.
Yan, Y. C., Zhao, R. Q., & Xing, T. T. (2019). Strategic introduction of the marketplace channel under dual upstream disadvantages in sales efficiency and demand information. European Journal of Operational Research, 273(3), 968–982.
Yang, D. H., & Gao, X. (2017). Online retailer recommender systems: A competitive analysis. International Journal of Production Research, 55(14), 4089–4109.
Yu, Y., Sun, L., & Guo, X. (2020). Dual-channel decision in a shopping complex when considering consumer channel preference. Journal of the Operational Research Society, 71(10), 1638–1656.
Yue, X., & Liu, J. (2006). Demand forecast sharing in a dual-channel supply chain. European Journal of Operational Research, 174(1), 646–667.
Zennyo, Y. (2020). Strategic contracting and hybrid use of agency and wholesale contracts in e-commerce platforms. European Journal of Operational Research, 281(1), 231–239.
Zhang, J. L., & Chen, J. (2013). Coordination of information sharing in a supply chain. International Journal of Production Economics, 143(1), 178–187.
Zhang, Q., Tang, W., Zaccour, G., & Zhang, J. (2019). Should a manufacturer give up pricing power in a vertical information-sharing channel? European Journal of Operational Research, 276(3), 910–928.
Zhang, S. C., & Zhang, J. X. (2020). Agency selling or reselling: E-tailer information sharing with supplier offline entry. European Journal of Operational Research, 280(1), 134–151.
Zhao, D. Z., & Li, Z. B. (2018). The impact of manufacturer’s encroachment and nonlinear production cost on retailer’s information sharing decisions. Annals of Operations Research, 264(1–2), 499–539.
Zhou, M. S., Dan, B., Ma, S. X., & Zhang, X. M. (2017). Supply chain coordination with information sharing: The informational advantage of GPOs. European Journal of Operational Research, 256(3), 785–802.
Zhou, Y.-W., Guo, J., & Zhou, W. (2018). Pricing/service strategies for a dual-channel supply chain with free riding and service-cost sharing. International Journal of Production Economics, 196, 198–210.
Zhou, Z. Z., & Zhu, K. X. (2010). The effects of information transparency on suppliers, manufacturers, and consumers in online markets. Marketing Science, 29(6), 1125–1137.
Acknowledgements
The authors are grateful to the editor and the anonymous reviewers for their valuable and constructive comments. This study was supported by the Major Program of the National Social Science Foundation of China [No. 18ZDA060].
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Lemma 1
Under mode RN, the expected profit of the platform is given as:
Taking the first order derivative of \(\pi_{P}^{RN}\) with respect to \(p^{RN}\) and \(s^{RN}\), we can derive
Let \(\frac{{\partial \pi_{P}^{RN} }}{{\partial p^{RN} }} = 0\), and \(\frac{{\partial \pi_{P}^{RN} }}{{\partial s^{RN} }} = 0\), we have
The Hessian matrix is:
To guarantee the profit function is concave and quadratic with \(p^{RN} \left( {w^{RN} } \right)\) and \(s^{RN} \left( {w^{RN} } \right)\), \(\eta > \eta_{{0}}\) should be satisfied, where \(\eta_{{0}} { = }\frac{{\gamma^{2} }}{2}\).
Under mode RN, the manufacturer does not know the demand information, and the manufacturer decides the wholesale price based on the expected demand \(E\left[ {q^{RN} } \right]\). The expected profit of the manufacturer is \(\pi_{M}^{RN} = E\left[ {w^{RN} q^{RN} } \right]\). Substituting \(p^{RN} \left( {w^{RN} } \right)\) and \(s^{RN} \left( {w^{RN} } \right)\) into the expected profit of the manufacturer, we obtain that \(\frac{{\partial \pi_{M}^{RN} }}{{\partial w^{RN} }} = \frac{{\eta \left( {a_{0} - 2w^{RN} } \right)}}{{2\eta - \gamma^{2} }}\), and \(\frac{{\partial^{2} \pi_{M}^{RN} }}{{\partial \left( {w^{RN} } \right)^{2} }} = - \frac{2\eta }{{2\eta - \gamma^{2} }}\). Since \(\eta > \eta_{{0}}\), it is obvious \(\frac{{\partial^{2} \pi_{M}^{RN} }}{{\partial \left( {w^{RN} } \right)^{2} }} < 0\). The expected profit of the manufacturer is concave in \(w^{RN}\), and we have the optimal wholesale price is \(w^{RN * } = \frac{{a_{0} }}{2}\).
Substituting \(w^{RN * } = \frac{{a_{0} }}{2}\) into \(p^{RN} \left( {w^{RN} } \right)\) and \(s^{RN} \left( {w^{RN} } \right)\), the equilibrium solutions of mode RN are \(p^{RN * } = \frac{{a_{0} \left( {\eta \left( {3 - 2z} \right) - \gamma^{2} } \right) + 2\eta zf}}{{2\left( {2\eta - \gamma^{2} } \right)}}\) and \(s^{RN * } = \frac{{\gamma \left( {a_{0} \left( {1 - 2z} \right) + 2zf} \right)}}{{2\left( {2\eta - \gamma^{2} } \right)}}\). Based on the equilibrium solutions of mode RN, the ex ante profits are \(\pi_{M}^{RN * } = \frac{{\eta a_{0}^{2} }}{{4\left( {2\eta - \gamma^{2} } \right)}}\) and \(\pi_{P}^{RN * } = \frac{{\eta \left( {a_{0}^{2} + 4z\sigma_{0}^{2} } \right)}}{{8\left( {2\eta - \gamma^{2} } \right)}}\).
The proof of equilibrium solutions under mode RS is similar to that under mode RN. Under mode RS, the expected profit of the platform is \(\pi_{P}^{RS} = E\left[ {\left( {p^{RS} - w^{RS} } \right)q^{RS} - \frac{\eta }{2}\left( {s^{RS} } \right)^{2} \left| f \right.} \right]\). And we have \(p^{RS} \left( {w^{RS} } \right) = \frac{{\eta E\left[ {\alpha \left| f \right.} \right] + w^{RS} \left( {\eta - \gamma^{2} } \right)}}{{2\eta - \gamma^{2} }}\), and \(s^{RS} \left( {w^{RS} } \right) = \frac{{\gamma \left( {E\left[ {\alpha \left| f \right.} \right] - w^{RS} } \right)}}{{2\eta - \gamma^{2} }}\).
The Hessian matrix is:
When \(\eta > \eta_{{0}}\), \(\left| H \right| = 2\eta - \gamma^{2} > 0\). And the objective function is concave. Under mode RS, the platform discloses the demand information. Therefore, the manufacturer makes decisions conditional on the demand signal \(E\left[ {q^{RS} \left| f \right.} \right]\). The expected profit of the manufacturer is:
Substituting \(p^{RS} \left( {w^{RS} } \right)\) and \(s^{RS} \left( {w^{RS} } \right)\) into the expected profit of the manufacturer, we obtain that \(\frac{{\partial \pi_{M}^{RS} }}{{\partial w^{RS} }} = \frac{{\eta \left( {E\left[ {\alpha \left| f \right.} \right] - 2w^{RS} } \right)}}{{2\eta - \gamma^{2} }}\) and \(\frac{{\partial^{2} \pi_{M}^{RS} }}{{\partial \left( {w^{RS} } \right)^{2} }} = - \frac{2\eta }{{2\eta - \gamma^{2} }} < 0\).
Let the first order condition \(\frac{{\partial \pi_{M}^{RS} }}{{\partial w^{RS} }} = 0\), the optimal wholesale price is derived, that is \(w^{RS * } = \frac{{a_{0} \left( {1 - z} \right) + zf}}{2}\). Substituting \(w^{RS * } = \frac{{a_{0} \left( {1 - z} \right) + zf}}{2}\) into \(p^{RS} \left( {w^{RS} } \right)\) and \(s^{RS} \left( {w^{RS} } \right)\), the equilibrium solutions and the ex ante profits of mode RS are derived as follows.
Proof of Proposition 1
In the reselling contract, \(w^{RN * } - w_{B}^{RN * } = 0\), \(p^{RN * } - p_{B}^{RN * } = \frac{{\gamma^{2} \left( {a_{0} \left( {1 - 2z} \right) + 2fz} \right)}}{{4\left( {2\eta - \gamma^{2} } \right)}}\), \(q^{RN * } - q_{B}^{RN * } = \frac{{\gamma^{2} \left( {a_{0} \left( {1 - 2z} \right) + 2fz} \right)}}{{4\left( {2\eta - \gamma^{2} } \right)}}\); \(w^{RS * } - w_{B}^{RS * } = 0\), \(p^{RS * } - p_{B}^{RS * } = \frac{{\gamma^{2} \left( {a_{0} \left( {1 - z} \right) + fz} \right)}}{{4\left( {2\eta - \gamma^{2} } \right)}}\), \(q^{RS * } - q_{B}^{RS * } = \frac{{\gamma^{2} \left( {a_{0} \left( {1 - z} \right) + fz} \right)}}{{4\left( {2\eta - \gamma^{2} } \right)}}\). Based on the equilibrium solutions in Lemmas 1 and 3, we can derive that \(w^{RN * } = w_{B}^{RN * }\), \(p^{RN * } > p_{B}^{RN * }\), \(q^{RN * } > q_{B}^{RN * }\); \(w^{RS * } = w_{B}^{RS * }\), \(p^{RS * } > p_{B}^{RS * }\), \(q^{RS * } > q_{B}^{RS * }\).
In the agency contract, \(p^{AN * } - p_{B}^{AN * } = \frac{{a_{0} \theta \gamma^{2} }}{{2\left( {\eta - \theta \gamma^{2} } \right)}}\), \(q^{AN * } - q_{B}^{AN * } = 0\); \(p^{AS * } - p_{B}^{AS * } = \frac{{\theta \gamma^{2} \left( {a_{0} \left( {1 - z} \right) + fz} \right)}}{{2\left( {\eta - \theta \gamma^{2} } \right)}}\), \(q^{AS * } - q_{B}^{AS * } = 0\). It is easy to derive that \(p^{AN * } > p_{B}^{AN * }\), \(q^{AN * } = q_{B}^{AN * }\); \(p^{AS * } > p_{B}^{AS * }\), \(q^{AS * } = q_{B}^{AS * }\).
Proof of Proposition 2
Based on the equilibrium solutions in Lemmas 1–3, when \(0 < \eta \le \eta_{0}\), the platform can only choose the non-recommendation scenario under the reselling contract. When \(\eta > \eta_{0}\), we can obtain that \(\pi_{P}^{RN * } - \pi_{BP}^{RN * } = \frac{{\gamma^{2} \left( {a_{0}^{2} + 4z\sigma_{0}^{2} } \right)}}{{16\left( {2\eta - \gamma^{2} } \right)}} > 0\), \(\pi_{P}^{RS * } - \pi_{BP}^{RS * } = \frac{{\gamma^{2} \left( {a_{0}^{2} + z\sigma_{0}^{2} } \right)}}{{16\left( {2\eta - \gamma^{2} } \right)}} > 0\). Under the agency contract, the platform can only choose the non-recommendation scenario when \(0 < \eta \le \eta_{1}\). When \(\eta > \eta_{1}\), we can derive that \(\pi_{P}^{AN * } - \pi_{BP}^{AN * } = \frac{{a_{0}^{2} \theta^{2} \gamma^{2} \left( {\eta - 2\theta \gamma^{2} } \right)}}{{8\left( {\eta - \theta \gamma^{2} } \right)^{2} }}\), \(\pi_{P}^{AS * } - \pi_{BP}^{AS * } = \frac{{\theta^{2} \gamma^{2} \left( {\eta - 2\theta \gamma^{2} } \right)\left( {a_{0}^{2} + z\sigma_{0}^{2} } \right)}}{{8\left( {\eta - \theta \gamma^{2} } \right)^{2} }}\). As a relust, if \(\eta_{1} < \eta \le \eta_{2}\), \(\pi_{P}^{AN * } < \pi_{BP}^{AN * }\), \(\pi_{P}^{AS * } < \pi_{BP}^{AS * }\); otherwise, \(\pi_{P}^{AN * } > \pi_{BP}^{AN * }\), \(\pi_{P}^{AS * } > \pi_{BP}^{AS * }\), where \(\eta_{0} = \frac{{\gamma^{2} }}{2}\), \(\eta_{1} = \frac{{3\theta \gamma^{2} }}{2}\), \(\eta_{2} = 2\theta \gamma^{2}\).
Proof of Proposition 3
Based on the equilibrium solutions of the reselling contract, the value of information sharing under the recommendation scenario and non-recommendation scenario are obtained. Under the recommendation cenario, we have \(v_{P}^{R} = \pi_{P}^{RS * } - \pi_{P}^{RN * } = - \frac{{3z\eta \sigma_{0}^{2} }}{{8\left( {2\eta - \gamma^{2} } \right)}}\), \(v_{M}^{R} = \pi_{M}^{RS * } - \pi_{M}^{RN * } = \frac{{z\eta \sigma_{0}^{2} }}{{4\left( {2\eta - \gamma^{2} } \right)}}\), and \(v^{R} = \left( {\pi_{M}^{RS * } + \pi_{P}^{RS * } } \right) - \left( {\pi_{M}^{RN * } + \pi_{P}^{RN * } } \right) = - \frac{{z\eta \sigma_{0}^{2} }}{{8\left( {2\eta - \gamma^{2} } \right)}}\); and under the non-receommendation scenario, we have \(v_{BP}^{R} = \pi_{BP}^{RS * } - \pi_{BP}^{RN * } = - \frac{{3z\sigma_{0}^{2} }}{16}\), \(v_{BM}^{R} = \pi_{BM}^{RS * } - \pi_{BM}^{RN * } = \frac{{z\sigma_{0}^{2} }}{8}\), and \(v_{B}^{R} = \left( {\pi_{BM}^{RS * } + \pi_{BP}^{RS * } } \right) - \left( {\pi_{BM}^{RN * } + \pi_{BP}^{RN * } } \right) = - \frac{{z\sigma_{0}^{2} }}{16}\). Since \(\eta > \eta_{0}\) in Lemma 1, we have \(v_{P}^{R} < 0\), \(v_{M}^{R} > 0\), \(v^{R} < 0\), \(v_{BP}^{R} < 0\), \(v_{BM}^{R} > 0\), and \(v_{B}^{R} < 0\).
Proof of Proposition 4
Based on the results given in the proof of Proposition 3, and \(z = {{\sigma_{{0}}^{{2}} } \mathord{\left/ {\vphantom {{\sigma_{{0}}^{{2}} } {\left( {\sigma_{{0}}^{{2}} + \sigma_{r}^{{2}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sigma_{{0}}^{{2}} + \sigma_{r}^{{2}} } \right)}}\), it is easy to verify the results in Table
3.
As shown in Table 3, we can prove the Proposition 4. For the manufacturer, \(\frac{{\partial v_{BM}^{R} }}{{\partial \sigma_{0} }} > 0\), \(\frac{{\partial v_{BM}^{R} }}{{\partial \sigma_{r} }} < 0\), \(\frac{{\partial v_{M}^{R} }}{{\partial \sigma_{0} }} > 0\), \(\frac{{\partial v_{M}^{R} }}{{\partial \sigma_{r} }} < 0\). For the platform, \(\frac{{\partial v_{BP}^{R} }}{{\partial \sigma_{0} }} < 0\), \(\frac{{\partial v_{BP}^{R} }}{{\partial \sigma_{r} }} > 0\), \(\frac{{\partial v_{P}^{R} }}{{\partial \sigma_{0} }} < 0\), \(\frac{{\partial v_{P}^{R} }}{{\partial \sigma_{r} }} > 0\). For the supply chain, \(\frac{{\partial v_{B}^{R} }}{{\partial \sigma_{0} }} < 0\), \(\frac{{\partial v_{B}^{R} }}{{\partial \sigma_{r} }} > 0\), \(\frac{{\partial v^{R} }}{{\partial \sigma_{0} }} < 0\), \(\frac{{\partial v^{R} }}{{\partial \sigma_{r} }} > 0\).
Proof of Proposition 5
Based on the equilibrium solutions of the agency contract, the value of information sharing under the recommendation scenario and non-recommendation scenario are obtained. Under the recommendation cenario, we have \(v_{P}^{A} = \pi_{P}^{AS * } - \pi_{P}^{AN * } = \frac{{z\eta \theta \sigma_{0}^{2} \left( {2\eta - 3\theta \gamma^{2} } \right)}}{{8\left( {\eta - \theta \gamma^{2} } \right)^{2} }}\), \(v_{M}^{A} = \pi_{M}^{AS * } - \pi_{M}^{AN * } = \frac{{z\eta \sigma_{0}^{2} \left( {1 - \theta } \right)}}{{4\left( {\eta - \theta \gamma^{2} } \right)}}\), and \(v^{A} = \left( {\pi_{M}^{AS * } + \pi_{P}^{AS * } } \right) - \left( {\pi_{M}^{AN * } + \pi_{P}^{AN * } } \right) = \frac{{z\eta \sigma_{0}^{2} \left( {2\eta - \theta \gamma^{2} \left( {2 + \theta } \right)} \right)}}{{8\left( {\eta - \theta \gamma^{2} } \right)^{2} }}\); and under the non-receommendation scenario, we have \(v_{BP}^{A} = \pi_{BP}^{AS * } - \pi_{BP}^{AN * } = \frac{{z\theta \sigma_{0}^{2} }}{4}\), \(v_{BM}^{A} = \pi_{BM}^{AS * } - \pi_{BM}^{AN * } = \frac{{z\sigma_{0}^{2} \left( {1 - \theta } \right)}}{4}\), and \(v_{B}^{A} = \left( {\pi_{BM}^{AS * } + \pi_{BP}^{AS * } } \right) - \left( {\pi_{BM}^{AN * } + \pi_{BP}^{AN * } } \right) = \frac{{z\sigma_{0}^{2} }}{4}\).
To ensure that the manufacturer and the retailer participating in the game, the ex ante profits in Lemma 2 should satisfy the condition \(\eta > \eta_{1}\), and it is easy to derive \(v_{P}^{A} > 0\),\(v_{M}^{A} > 0\), \(v^{A} > 0\), \(v_{BP}^{A} > 0\), \(v_{BM}^{A} > 0\), and \(v_{B}^{A} > 0\).
Proof of Proposition 6
Based on the results given in the proof of Proposition 5, and \(z = {{\sigma_{{0}}^{{2}} } \mathord{\left/ {\vphantom {{\sigma_{{0}}^{{2}} } {\left( {\sigma_{{0}}^{{2}} + \sigma_{r}^{{2}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sigma_{{0}}^{{2}} + \sigma_{r}^{{2}} } \right)}}\), it is easy to verify the results in Table
4.
As shown in Table 4, we can prove the Proposition 6. For the platform, \(\frac{{\partial v_{BP}^{A} }}{{\partial \sigma_{0} }} > 0\), \(\frac{{\partial v_{BP}^{A} }}{{\partial \sigma_{r} }} < 0\), \(\frac{{\partial v_{P}^{A} }}{{\partial \sigma_{0} }} > 0\), \(\frac{{\partial v_{P}^{A} }}{{\partial \sigma_{r} }} < 0\). For the manufacturer, \(\frac{{\partial v_{BM}^{A} }}{{\partial \sigma_{0} }} > 0\), \(\frac{{\partial v_{BM}^{A} }}{{\partial \sigma_{r} }} < 0\), \(\frac{{\partial v_{M}^{A} }}{{\partial \sigma_{0} }} > 0\), \(\frac{{\partial v_{M}^{A} }}{{\partial \sigma_{r} }} < 0\). For the supply chain, \(\frac{{\partial v_{B}^{A} }}{{\partial \sigma_{0} }} > 0\), \(\frac{{\partial v_{B}^{A} }}{{\partial \sigma_{r} }} < 0\), \(\frac{{\partial v^{A} }}{{\partial \sigma_{0} }} > 0\), \(\frac{{\partial v^{A} }}{{\partial \sigma_{r} }} < 0\).
Proof of Proposition 7
From Propositions 3 and 5, we can derive that the potential optimal strategies for the platform are mode BRN, mode BAS, mode RN, and mode AS. Since \(0 < \theta < \frac{1}{2}\), we derive that \(\left\{ {\begin{array}{*{20}c} {\eta_{0} > \eta_{2} > \eta_{1} ,} & {0 < \theta < \frac{1}{4}} \\ {\eta_{2} > \eta_{0} > \eta_{1} ,} & {\frac{1}{4} < \theta < \frac{1}{3}} \\ {\eta_{2} > \eta_{1} > \eta_{0} ,} & {\frac{1}{3} < \theta < \frac{1}{2}} \\ \end{array} } \right.\).
-
(i)
When \(0 < \theta < \frac{1}{4}\), \(\eta_{0} > \eta_{2} > \eta_{1}\), the platfrom’s optiaml strategy is given as follows:
-
(a)
When \(0 < \theta < \frac{1}{4}\), \(0 < \eta \le \eta_{1}\), the platform can only choose the non-recommendation scenario in two contracts. Therefore, the platfrom’s optiaml strategy can be obtained by comparing mode BRN and mode BAS. From Lemma 3, we have the following result: \(\pi_{BP}^{RN * } - \pi_{BP}^{AS * } = \frac{{a_{0}^{2} \left( {1 - 4\theta } \right) + 4z\sigma_{0}^{2} \left( {1 - \theta } \right)}}{16}\). Since \(0 < \theta < \frac{1}{4}\), \(0 < \eta \le \eta_{1}\), it is easy to obtain \(\pi_{BP}^{RN * } > \pi_{BP}^{AS * }\).
-
(b)
When \(0 < \theta < \frac{1}{4}\), \(\eta_{1} < \eta \le \eta_{2}\), the platform can only choose non-recommendation scenario in the reselling contract, but non-recommendation scenario and recommendation scenario are meaningful in the agency contract. The results in Proposition 2 show that the platform still prefers the non-recommendation scenario when \(\eta_{1} < \eta \le \eta_{2}\) in the agency contract. Hence, \(\pi_{BP}^{RN * } > \pi_{BP}^{AS * }\) still holds.
-
(c)
When \(0 < \theta < \frac{1}{4}\), \(\eta_{2} < \eta \le \eta_{0}\), the platform still prefers mode BRN under the reselling contract. However, under the agecny contract, we have \(\pi_{P}^{AS * } > \pi_{BP}^{AS * }\). Therefore, by comparing mode BRN and mode AS, we have \(\pi_{BP}^{RN * } - \pi_{P}^{AS * } = \frac{1}{16}\left( {a_{0}^{2} + 4z\sigma_{0}^{2} - \frac{{2\eta \theta \left( {2\eta - 3\theta \gamma^{2} } \right)\left( {a_{0}^{2} + z\sigma_{0}^{2} } \right)}}{{\left( {\eta - \theta \gamma^{2} } \right)^{2} }}} \right) > 0\). As a result, when \(0 < \theta < \frac{1}{4}\), \(0 < \eta \le \eta_{0}\), the platform prefers mode BRN.
-
(d)
When \(0 < \theta < \frac{1}{4}\), \(\eta > \eta_{0}\), we have \(\pi_{P}^{RN * } > \pi_{BP}^{RN * }\) and \(\pi_{P}^{AS * } > \pi_{BP}^{AS * }\). Therefore, by comparing mode RN and mode AS, we obtain that \(\pi_{P}^{RN * } - \pi_{P}^{AS * } = \frac{1}{8}\eta \left( {\frac{{\theta \left( {3\theta \gamma^{2} - 2\eta } \right)\left( {a_{0}^{2} + z\sigma_{0}^{2} } \right)}}{{\left( {\eta - \theta \gamma^{2} } \right)^{2} }} + \frac{{a_{0}^{2} + 4z\sigma_{0}^{2} }}{{2\eta - \gamma^{2} }}} \right) > 0\). As a result, when \(0 < \theta < \frac{1}{4}\), \(0 < \eta \le \eta_{0}\), the platform will choose mode BRN; when \(\eta > \eta_{0}\), mode RN is preferred.
-
(a)
-
(ii)
When \(\frac{1}{4} < \theta < \frac{1}{3}\), \(\eta_{1} < \eta_{0} < \eta_{2}\), the conditions of the platform’s optimal strategy are complex.
-
(a)
When \(\frac{1}{4} < \theta < \frac{1}{3}\), \(0 < \eta \le \eta_{1}\), the platform can only choose non-recommendation scenario in two contracts. When \(\frac{1}{4} < \theta < \frac{1}{3}\), \(\eta_{1} < \eta \le \eta_{0}\), the platform prefers non-recommendation scenario in two contracts though both non-recommendation scenario and recommendation scenario are meaningful in the agency contract. Hence, we have \(\pi_{BP}^{RN * } - \pi_{BP}^{AS * } = \frac{{a_{0}^{2} \left( {1 - 4\theta } \right) + 4z\sigma_{0}^{2} \left( {1 - \theta } \right)}}{16}\). Let \(z_{BP} = \frac{{a_{0}^{2} \left( {4\theta - 1} \right)}}{{4\sigma_{0}^{2} \left( {1 - \theta } \right)}}\), then \(\pi_{BP}^{RN * } < \pi_{BP}^{AS * }\) if \(0 < z \le \min \{ z_{BP} ,{\kern 1pt} {\kern 1pt} 1\}\); \(\pi_{BP}^{RN * } > \pi_{BP}^{AS * }\) if \(\min \{ z_{BP} ,{\kern 1pt} {\kern 1pt} 1\} < z < 1\).
-
(b)
When \(\frac{1}{4} < \theta < \frac{1}{3}\), \(\eta_{0} < \eta \le \eta_{2}\), the platform can choose the non-recommendation scenario and recommendation scenario in both contracts. Since \(\pi_{P}^{RN * } > \pi_{BP}^{RN * }\) and \(\pi_{P}^{AS * } < \pi_{BP}^{AS * }\), we have \(\pi_{BP}^{AS * } - \pi_{P}^{RN * } = \frac{1}{8}\left( {2\theta \left( {a_{0}^{2} + z\sigma_{0}^{2} } \right) - \frac{{\eta \left( {a_{0}^{2} + 4z\sigma_{0}^{2} } \right)}}{{2\eta - \gamma^{2} }}} \right) < 0\). Hence, mode RN is chosen.
-
(c)
When \(\frac{1}{4} < \theta < \frac{1}{3}\), \(\eta > \eta_{2}\), we have \(\pi_{P}^{RN * } - \pi_{P}^{AS * } = \frac{\eta }{8}\left( {\frac{{\theta \left( {3\theta \gamma^{2} - 2\eta } \right)\left( {a_{0}^{2} + z\sigma_{0}^{2} } \right)}}{{\left( {\eta - \theta \gamma^{2} } \right)^{2} }} + \frac{{a_{0}^{2} + 4z\sigma_{0}^{2} }}{{2\eta - \gamma^{2} }}} \right)\).
Let \(z_{P} = \frac{{a_{0}^{2} \left( {2\theta^{2} \gamma^{4} - 6\eta \theta^{2} \gamma^{2} - \eta^{2} \left( {1 - 4\theta } \right)} \right)}}{{\sigma_{0}^{2} \left( {\theta^{2} \gamma^{4} + 4\eta^{2} \left( {1 - \theta } \right) - 6\eta \theta \gamma^{2} \left( {1 - \theta } \right)} \right)}}\), when \(\eta > \eta_{2}\) and \(0 < z < \min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{P} \} ,{\kern 1pt} {\kern 1pt} 1\}\), \(\pi_{P}^{RN * } < \pi_{P}^{AS * }\); when \(\eta > \eta_{2}\) and \(\min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{p} \} ,{\kern 1pt} {\kern 1pt} 1\} < z < 1\), \(\pi_{P}^{RN * } > \pi_{P}^{AS * }\).
-
(a)
-
(iii)
When \(\frac{1}{3} < \theta < \frac{1}{2}\), \(\eta_{0} < \eta_{1} < \eta_{2}\), the conditions of the platform’s optimal strategy are given as follows.
-
(a)
When \(\frac{1}{3} < \theta < \frac{1}{2}\), \(0 < \eta \le \eta_{0}\); the platform prefers non-recommendatin scenario under two contracts. Hence, \(\pi_{BP}^{RN * } < \pi_{BP}^{AS * }\) if \(0 < z < \min \{ z_{BP} ,{\kern 1pt} {\kern 1pt} 1\}\); \(\pi_{BP}^{RN * } > \pi_{BP}^{AS * }\) if \(\min \{ z_{BP} ,{\kern 1pt} {\kern 1pt} 1\} < z < 1\).
-
(b)
When \(\frac{1}{3} < \theta < \frac{1}{2}\), \(\eta_{0} < \eta \le \eta_{1}\); or \(\frac{1}{3} < \theta < \frac{1}{2}\), \(\eta_{1} < \eta \le \eta_{2}\), the platform always prefers mode RN under the reselling contract and mode BAS under the agency contact. Hence, \(\pi_{BP}^{AS * } - \pi_{P}^{RN * } = \frac{1}{8}\left( {2\theta \left( {a_{0}^{2} + z\sigma_{0}^{2} } \right) - \frac{{\eta \left( {a_{0}^{2} + 4z\sigma_{0}^{2} } \right)}}{{2\eta - \gamma^{2} }}} \right) < 0\).
-
(c)
When \(\frac{1}{3} < \theta < \frac{1}{2}\), \(\eta > \eta_{2}\), the results are same as proved above. Hence, we obtain the results in Proposition 7.
-
(a)
Proof of Corollary 1
Given the platform’s optimal strategy, if the manufacturer can better off, the manufacturer will accept this contract.
-
(i)
When \(0 < \theta < \frac{1}{4}\), the platform’s optiaml strategy is mode BRN or mode RN.
-
(a)
When \(0 < \theta < \frac{1}{4}\), \(0 < \eta \le \eta_{1}\), the platfrom’s optiaml strategy is mode BRN. However, given the platform’s strategy, \(\pi_{BM}^{RN * } - \pi_{BM}^{AS * } = - \frac{{a_{0}^{2} \left( {1 - 2\theta } \right) + 2z\sigma_{0}^{2} \left( {1 - \theta } \right)}}{8} < 0\). Hence, the manufacturer is worse off in mode BRN. Similarly, when \(0 < \theta < \frac{1}{4}\), \(\eta_{1} < \eta \le \eta_{2}\), we have \(\pi_{BM}^{RN * } - \pi_{BM}^{AS * } < 0\). When \(0 < \theta < \frac{1}{4}\), \(\eta_{2} < \eta \le \eta_{0}\), we have \(\pi_{BM}^{RN * } - \pi_{M}^{AS * } = \frac{{a_{0}^{2} \left( {\theta \left( {2\eta - \gamma^{2} } \right) - \eta } \right) - 2z\eta \sigma_{0}^{2} \left( {1 - \theta } \right)}}{{8\left( {\eta - \theta \gamma^{2} } \right)}} < 0\). Hence, when \(0 < \eta \le \eta_{0}\), the platform and the manufacturer can not reach a consensus.
-
(b)
When \(0 < \theta < \frac{1}{4}\), \(\eta > \eta_{0}\), we have \(\pi_{M}^{RN * } - \pi_{M}^{AS * } = \frac{{\eta a_{0}^{2} \left( {\gamma^{2} - \eta } \right)\left( {1 - 2\theta } \right)}}{{4\left( {2\eta - \gamma^{2} } \right)\left( {\eta - \theta \gamma^{2} } \right)}} - \frac{{z\sigma_{0}^{2} \eta \left( {1 - \theta } \right)}}{{4\left( {\eta - \theta \gamma^{2} } \right)}}\). Let \(z_{M} = \frac{{a_{0}^{2} \left( {\gamma^{2} - \eta } \right)\left( {1 - 2\theta } \right)}}{{\sigma_{0}^{2} \left( {2\eta - \gamma^{2} } \right)\left( {1 - \theta } \right)}}\), when \(0 < z < \min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{M} \} ,{\kern 1pt} {\kern 1pt} 1\}\), \(\pi_{M}^{RN * } > \pi_{M}^{AS * }\); when \(\min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{M} \} ,{\kern 1pt} {\kern 1pt} 1\} < z < 1\), \(\pi_{M}^{RN * } < \pi_{M}^{AS * }\). As a result, when \(0 < \theta < \frac{1}{4}\), \(\eta > \eta_{0}\), \(0 < z < \min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{M} \} ,{\kern 1pt} {\kern 1pt} 1\}\), the platform’s and manufacturer’s optimal strategy is mode RN, and they can achieve a win–win situation.
-
(a)
-
(ii)
When \(\frac{1}{4} < \theta < \frac{1}{2}\), the proof process is similar, and we obtain the results as follows.
-
(a)
When \(\frac{1}{4} < \theta < \frac{1}{2}\), \(0 < \eta \le \eta_{0}\), and \(0 < z < \min \{ z_{BP} ,{\kern 1pt} {\kern 1pt} 1\}\), mode BAS makes the manufacturer better off. In addition, when \(\frac{1}{4} < \theta < \frac{1}{2}\), \(\eta_{0} < \eta \le \eta_{2}\), mode RN makes the manufacturer better off.
-
(b)
When \(\frac{1}{4} < \theta < \frac{1}{2}\), \(\eta > \eta_{2}\), the optimal strategy for the platform and the manufacturer is affected by the information accuracy. For the platform, if \(0 < z < \min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{P} \} ,{\kern 1pt} {\kern 1pt} 1\}\), \(\pi_{P}^{RN * } < \pi_{P}^{AS * }\); if \(\eta > \eta_{2}\) and \(\min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{p} \} ,{\kern 1pt} {\kern 1pt} 1\} < z < 1\), \(\pi_{P}^{RN * } > \pi_{P}^{AS * }\). For the manufacturer, if \(0 < z < \min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{M} \} ,{\kern 1pt} {\kern 1pt} 1\}\), \(\pi_{M}^{RN * } > \pi_{M}^{AS * }\); if \(\min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{M} \} ,{\kern 1pt} {\kern 1pt} 1\} < z < 1\), \(\pi_{M}^{RN * } < \pi_{M}^{AS * }\). Through analyzing, we obtain that \(z_{P} < z_{M}\) if \(\eta_{2} < \eta < \eta_{3}\); and \(z_{P} > z_{M}\) if \(\eta > \eta_{3}\). Therefore, when \(\frac{1}{4} < \theta < \frac{1}{2}\), \(\eta_{2} < \eta < \eta_{3}\), \(\min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{p} \} ,{\kern 1pt} {\kern 1pt} 1\} < z < \min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{M} \} ,{\kern 1pt} {\kern 1pt} 1\}\), mode RN makes the manufacturer better off; When \(\frac{1}{4} < \theta < \frac{1}{2}\), \(\eta > \eta_{3}\), \(\min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{M} \} ,{\kern 1pt} {\kern 1pt} 1\} < z < \min \{ \max \{ 0,{\kern 1pt} {\kern 1pt} z_{P} \} ,{\kern 1pt} {\kern 1pt} 1\}\), mode AS makes the manufacturer better off, where \(\eta_{3} = \frac{{\gamma^{2} }}{4}\left( {3 + \sqrt {\frac{{9 - 33\theta + 32\theta^{2} }}{1 - \theta }} } \right)\).
-
(a)
Proof of Corollary 2
It is easy to derive that \(\frac{{\partial z_{BP} }}{\partial \eta } = 0\), \(\frac{{\partial z_{M} }}{\partial \eta } = - \frac{{a_{0}^{2} \gamma^{2} \left( {1 - 2\theta } \right)}}{{\sigma_{0}^{2} \left( {2\eta - \gamma^{2} } \right)^{2} \left( {1 - \theta } \right)}} < 0\), and \(\frac{{\partial z_{P} }}{\partial \eta } = \frac{{6a_{0}^{2} \gamma^{2} \theta \left( {\eta - \theta \gamma^{2} } \right)\left( {\eta \left( {1 - \theta } \right) - \theta \gamma^{2} \left( {2 - 3\theta } \right)} \right)}}{{\sigma_{0}^{2} \left( {4\eta^{2} \left( {1 - \theta } \right) - 6\eta \theta \gamma^{2} \left( {1 - \theta } \right) + \gamma^{4} \theta^{2} } \right)^{2} }} > 0\).
1.1 Proof of the equilibrium solutions for mode BHN and mode BHS
Given the hybrid contract of the non-recommendation scenario, there exist equilibrium solutions for mode BHN and mode BHS, respectively. The optimal decisions are as follows:
-
(i)
\(w_{B}^{HN * } = \frac{{a_{0} \left( {1 - \theta } \right)}}{{2\left( {1 + \beta } \right)}}\left( {\frac{\beta }{1 - \beta } + \frac{{\phi \left( {8 + \beta \left( {8\theta - \beta^{2} \left( {1 + \theta } \right)^{2} } \right)} \right)}}{{8\left( {1 - \theta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} }}} \right)\), \(p_{BM}^{HN * } { = }\frac{{a_{0} }}{{2\left( {1 - \beta^{2} } \right)}}\left( {1 - \phi + \frac{{\beta \phi \left( {2\left( {5 - 3\theta } \right) - \beta^{2} \left( {1 - \theta^{2} } \right)} \right)}}{{8\left( {1 - \theta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} }}} \right)\), \(p_{BP}^{HN * } = \frac{1}{2}\left( {\phi \left( {a_{0} \left( {1 - z} \right) + zf} \right) + \frac{{a_{0} }}{1 + \beta }\left( {\frac{\beta }{1 - \beta } + \frac{{\phi \left( {4\left( {1 - \theta } \right)\left( {1 - \beta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} } \right)}}{{8\left( {1 - \theta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} }}} \right)} \right)\);
-
(ii)
\(w_{B}^{HS * } { = }\frac{{\left( {1 - \theta } \right)\left( {a_{0} \left( {1 - z} \right) + zf} \right)}}{{2\left( {1 + \beta } \right)}}\left( {\frac{\beta }{1 - \beta } + \frac{{\phi \left( {8 + \beta \left( {8\theta - \beta^{2} \left( {1 + \theta } \right)^{2} } \right)} \right)}}{{8\left( {1 - \theta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} }}} \right)\), \(p_{BM}^{HS * } = \frac{{\left( {a_{0} \left( {1 - z} \right) + zf} \right)}}{{2\left( {1 - \beta^{2} } \right)}}\left( {1 - \phi + \frac{{\beta \phi \left( {2\left( {5 - 3\theta } \right) - \beta^{2} \left( {1 - \theta^{2} } \right)} \right)}}{{8\left( {1 - \theta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} }}} \right)\), \(p_{BP}^{HS * } { = }\frac{{\left( {a_{0} \left( {1 - z} \right) + zf} \right)}}{2}\left( {\phi + \frac{1}{1 + \beta }\left( {\frac{\beta }{1 - \beta } + \frac{{\phi \left( {4\left( {1 - \theta } \right)\left( {1 - \beta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} } \right)}}{{8\left( {1 - \theta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} }}} \right)} \right)\).
1.2 Proof of the equilibrium solutions for mode HN and mode HS
Given the hybrid contract of recommendation scenario, there exist equilibrium solutions for mode HN and mode HS, respectively. The optimal decisions are as follows:
-
(i)
\(w^{HN * } = \frac{{a_{0} \eta \left( {1 - \theta } \right)\left( {H_{4} + H_{5} + H_{6} + H_{7} } \right)}}{{2\left( {H_{1} + H_{2} + H_{3} } \right)}}\), \(p_{M}^{HN * } = \frac{{a_{0} \eta \left( {2 - \phi \left( {2 - \beta } \right)} \right)}}{{H_{8} }} + \frac{{w^{HN * } \left( {\beta \eta \left( {3 - \theta } \right) - \phi \gamma^{2} \left( {\beta \phi \left( {2 - \theta } \right) + \left( {1 - \phi } \right)\left( {1 - \theta } \right)} \right)} \right)}}{{H_{8} \left( {1 - \theta } \right)}}\), \(s^{HN * } = \frac{{\gamma \left( {\phi \left( {\phi \left( {a_{0} \left( {1 - z} \right) + zf} \right) - w^{HN * } } \right) + p_{M}^{HN * } \left( {\beta \phi + \theta \left( {2 - \phi \left( {2 - \beta } \right)} \right)} \right)} \right)}}{{2\eta - \gamma^{2} \phi^{2} }}\), \(p_{P}^{HN * } = \frac{{\eta \phi \left( {a_{0} \left( {1 - z} \right) + zf} \right) + w^{HN * } \left( {\eta - \gamma^{2} \phi^{2} } \right) + p_{M}^{HN * } \left( {\beta \eta \left( {1 + \theta } \right) + \phi \theta \gamma^{2} \left( {1 - \phi } \right)} \right)}}{{2\eta - \gamma^{2} \phi^{2} }}\);
-
(ii)
\(w^{HS * } = \frac{{\eta \left( {1 - \theta } \right)\left( {a_{0} \left( {1 - z} \right) + zf} \right)\left( {H_{4} + H_{5} + H_{6} + H_{7} } \right)}}{{2\left( {H_{1} + H_{2} + H_{3} } \right)}}\), \(p_{M}^{HS * } = \frac{{\eta \left( {a_{0} \left( {1 - z} \right) + zf} \right)\left( {2 - \phi \left( {2 - \beta } \right)} \right)}}{{H_{8} }} + \frac{{w^{HS * } \left( {\beta \eta \left( {3 - \theta } \right) - \phi \gamma^{2} \left( {\beta \phi \left( {2 - \theta } \right) + \left( {1 - \phi } \right)\left( {1 - \theta } \right)} \right)} \right)}}{{H_{8} \left( {1 - \theta } \right)}}\), \(\begin{gathered} s^{HS * } = \frac{{w^{HS * } \gamma }}{{H_{8} }}\left( {\frac{{\beta \theta \left( {3 - \theta } \right)\left( {1 - \phi } \right) + \phi 2\beta^{2} }}{{\left( {1 - \theta } \right)}} - \phi \left( {2 - \theta \beta^{2} } \right)} \right) \\ + \frac{{\gamma \left( {a_{0} \left( {1 - z} \right) + zf} \right)\left( {\phi \left( {\beta + \left( {2 - \beta } \right)\phi } \right) + 2\theta \left( {1 - \phi } \right)\left( {1 - \phi \left( {1 - \beta } \right)} \right)} \right)}}{{H_{8} }} \\ \end{gathered}\), \(\begin{gathered} p_{P}^{HS * } = \frac{{\eta \left( {a_{0} \left( {1 - z} \right) + zf} \right)\left( {\beta \left( {1 + \theta } \right)\left( {1 - \phi } \right) + 2\phi } \right)}}{{H_{8} }} \\ + \frac{{w^{HS * } }}{{H_{8} }}\left( {2\eta - \theta \gamma^{2} + \frac{{\eta \beta^{2} \left( {1 + \theta } \right) + \phi \gamma^{2} \left( {\left( {\theta \left( {2 + \beta - \theta \left( {2 - \beta } \right)} \right) - \beta } \right) - \phi \left( {1 + \left( {1 - \beta } \right)\left( {1 - \theta - \theta^{2} } \right)} \right)} \right)}}{1 - \theta }} \right) \\ \end{gathered}\).
Where \(H_{1} = - \eta^{2} \left( {1 - \beta^{2} } \right)\left( {8\left( {1 - \theta } \right) + \beta^{2} \left( {1 + \theta } \right)^{2} } \right)\),
Rights and permissions
About this article
Cite this article
Chen, X., Li, B., Chen, W. et al. Influences of information sharing and online recommendations in a supply chain: reselling versus agency selling. Ann Oper Res 329, 717–756 (2023). https://doi.org/10.1007/s10479-021-03968-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-03968-7