Abstract
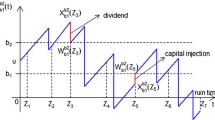
The paper features a hybrid dividend payment strategy on an insurance surplus with stochastic income. The hybrid dividend strategy works as follows: A delay-clock starts whenever the surplus up-shoots, due to a premium arrival, to a level between barriers ‘k’ and ‘\( \ell \)’, such that \( 0 \leqslant u \leqslant k \leqslant \ell < \infty \). Further, the clock restarts along with each premium or claim arrival, provided the surplus still lies between ‘k’ and ‘\( \ell \)’. However, when the surplus exits to a level outside the range between two barriers, the clock terminates. The insurer pays a dividend of an amount exceeding the level ‘k’ to shareholders on two scenarios. In one situation, the insurer pays dividend if delay-clock alarms before a premium or claim arrival. In the other situation, the insurer pays dividend instantaneously if surplus exceeds the second barrier ‘\( \ell \)’. The aggregate premiums and claims are both following mutually independent compound Poisson processes, both having exponential amount sizes which are further independent to corresponding inter-arrival times. A scheme for determining analytic expressions for piecewise Volterra integral equations, with boundary conditions, which are satisfied by the expected discounted dividend paid before ruin and the Gerber–Shiu function are discussed in detail when the delay-clock also follows an exponential distribution. We discuss a numerical example to show the tractability of the scheme and to brief the impact of hybrid dividend strategy over the classical De Finetti barrier strategy for paying dividends.



Similar content being viewed by others
References
Albrecher, H., Cheung, E. C., & Thonhauser, S. (2011). Randomised observation periods for the compound Poisson risk model: Dividends. ASTIN Bulletin: The Journal of the IAA, 41(2), 645–672.
Bao, Z.-H., & Ye, Z.-X. (2007). The Gerber-Shiu discounted penalty function in the delayed renewal risk process with random income. Applied Mathematics and Computation, 184(2), 857–863.
Beekman, J. A. (1985). A series for infinite time ruin probabilities. Insurance: Mathematics and Economics, 4(2), 129–134.
Boikov, A. V. (2003). The Cramer-Lundberg model with stochastic premium process. Theory of Probability & Its Applications, 47(3), 489–493.
Boucherie, R. J., & Boxma, O. J. (1996). The workload in the M/G/1 queue with work removal. Probability in the Engineering and Informational Sciences, 10(2), 261–277.
De Finetti, B. (1957). Su un’impostazione alternativa della teoria collettiva del rischio. In Transactions of the XVth international congress of Actuaries (Vol. 2, pp. 433–443). New York.
Dibu, A. S., Jacob, M. J., Papaioannou, A. D., & Ramsden, L. (2020). Delayed capital injections for a risk process with Markovian arrivals. Methodology and Computing in Applied Probability. https://doi.org/10.1007/s11009-020-09796-9.
Dong, H., Zhao, X. H., & Liu, Z. M. (2010). Risk process with barrier and random income. Applied Mathematics E-Notes, 10, 191–198.
Gerber, H. U., & Shiu, E. S. (1998). On the time value of ruin. North American Actuarial Journal, 2(1), 48–72.
Gerber, H. U., & Shiu, E. S. (2004). Optimal dividends: Analysis with Brownian motion. North American Actuarial Journal, 8(1), 1–20.
Labbé, C., & Sendova, K. P. (2009). The expected discounted penalty function under a risk model with stochastic income. Applied Mathematics and Computation, 215(5), 1852–1867.
Lin, X. S., Willmot, G. E., & Drekic, S. (2003). The classical risk model with a constant dividend barrier: Analysis of the Gerber-Shiu discounted penalty function. Insurance: Mathematics and Economics, 33(3), 551–566.
Melnikov, A. (2002). Risk analysis in finance and insurance. Boca Raton: CRC.
Sendova, K. P., Yang, C., & Zhang, R. (2018). Dividend barrier strategy: Proceed with caution. Statistics & Probability Letters, 137, 157–164.
Su, W., Shi, B., & Wang, Y. (2019). Estimating the Gerber-Shiu function under a risk model with stochastic income by Laguerre series expansion. Communications in Statistics-Theory and Methods, 49, 1–23.
Temnov, G. (2004). Risk process with random income. Journal of Mathematical Sciences, 123(1), 3780–3794.
Zhang, Z. (2016). Estimating the Gerber-Shiu function by Fourier-sinc series expansion. Scandinavian Actuarial Journal, 10, 1–22.
Zhang, Z., Eric, C., & Cheung, K. (2016). The Markov additive risk process under an Erlangized dividend barrier strategy. Methodology and Computing in Applied Probability, 18(2), 275.
Zhang, Z., & Yang, H. (2010). On a risk model with stochastic premiums income and dependence between income and loss. Journal of computational and applied mathematics, 234(1), 44–57.
Zhao, Y., & Yin, C. (2012). The expected discounted penalty function under a renewal risk model with stochastic income. Applied Mathematics and Computation, 218(10), 6144–6154.
Acknowledgements
We would like to thank the anonymous reviewers for their valuable suggestions on improving the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Dibu, A.S., Jacob, M.J. On a double barrier hybrid dividend strategy in a compound Poisson risk model with stochastic income. Ann Oper Res 315, 969–984 (2022). https://doi.org/10.1007/s10479-021-03937-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-03937-0
Keywords
- Compound Poisson risk model
- Double-barrier dividend
- Hybrid dividend
- Piecewise Volterra integral equation