Abstract
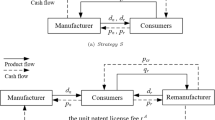
Manufacturers are increasingly taking positive actions to handle used products by adopting “recycling materials” (RM), “remanufacturing product” (RP) or the hybrid strategy combining with both RM and RP (RMP). Under each strategy, in addition to the optimal quantity and price of new product, manufacturers may also face important decisions on the optimal quantity and price of remanufactured product and (or) recycling materials. To address such challenging issues, we consider a manufacturer who sells a new product to consumers, and examine the optimal recovery strategy and associated decisions by developing three models, i.e., models without incorporating recovery strategy, with considering recovery strategy and both recovery strategy and government subsidy. We further explore the impacts of product quality and government subsidy on the optimal decisions. Our results show that, neither recovery strategy including not implementing recovery strategy is always superior to the others, which depends on cost savings from remanufacturing products and benefits of recycling materials. Interestingly, the manufacturer with a higher product quality prefers to choose RP but RM otherwise. Government subsidy increases the manufacturer’s profit under each recovery strategy. In general, government subsidy helps to increase consumer surplus but reduce environment impact. However, as government subsidy increases, the manufacturer may prefer to implement RMP rather than RP, which may result in less consumer surplus and more environmental impact. Therefore, a higher subsidy unexpectedly may lead to a lower social welfare. This suggests that, the government should design an appropriate and more practical subsidy policy to dispose used products.




Similar content being viewed by others
References
Abbey, J. D., Kleber, R., Souza, G. C., & Voigt, G. (2017). The role of perceived quality risk in pricing remanufactured products. Production and Operations Management,26(1), 100–115.
Agrawal, V. V., Atasu, A., & Van Ittersum, K. (2015). Remanufacturing, third-party competition, and consumers’ perceived value of new products. Management Science,61(1), 60–72.
Agrawal, V. V., Ferguson, M., & Souza, G. C. (2016). Trade-in rebates for price discrimination and product recovery. IEEE Transactions on Engineering Management,63(3), 326–339.
Agrawal, V. V., Ferguson, M., Toktay, L. B., & Thomas, V. M. (2012). Is leasing greener than selling? Management Science,58(3), 523–533.
Akan, M., Ata, B., & Savaşkan-Ebert, R. C. (2013). Dynamic pricing of remanufacturable products under demand substitution: A product life cycle model. Annals of Operations Research,211(1), 1–25.
Aksen, D., Aras, N., & Karaarslan, A. G. (2009). Design and analysis of government subsidized collection systems for incentive-dependent returns. International Journal of Production Economics,119(2), 308–327.
Atasu, A., Sarvary, M., & Van Wassenhove, L. N. (2008). Remanufacturing as a marketing strategy. Management Science,54(10), 1731–1746.
Atasu, A., & Souza, G. C. (2013). How does product recovery affect quality choice? Production and Operations Management,22(4), 991–1010.
Atasu, A., & Subramanian, R. (2012). Extended producer responsibility for e-waste: Individual or collective producer responsibility? Production and Operations Management,21(6), 1042–1059.
Atasu, A., & Van Wassenhove, L. N. (2012). An operations perspective on product take-back legislation for e-waste: Theory, practice, and research needs. Production and Operations Management,21(3), 407–422.
Baldé, C. P., Wang, F., Kuehr, R., & Huisman, J. (2015). The global e-waste monitor–2014. Bonn: United Nations University, IAS–SCYCLE.
Boone, T., Vaidyanathan, J., & Ganeshan, R. (Eds.). (2012). Sustainable supply chains: Models, methods, and public policy implications (Vol. 174). Berlin: Springer.
Calcott, P., & Walls, M. (2005). Waste, recycling, and “design for environment”: Roles for markets and policy instruments. Resource and Energy Economics,27(4), 287–305.
Debo, L. G., Toktay, L. B., & Van Wassenhove, L. N. (2005). Market segmentation and product technology selection for remanufacturable products. Management Science,51(8), 1193–1205.
Esenduran, G., Kemahlıoğlu-Ziya, E., & Swaminathan, J. M. (2016). Take-back legislation: Consequences for remanufacturing and environment. Decision Sciences,47(2), 219–256.
Esenduran, G., Kemahlıoğlu-Ziya, E., & Swaminathan, J. M. (2017). Impact of take-back regulation on the remanufacturing industry. Production and Operations Management,26(5), 924–944.
Ferguson, M. E., & Toktay, L. B. (2006). The effect of competition on recovery strategies. Production and Operations Management,15(3), 351–368.
Ferrer, G. (1996). Market segmentation and product line design in remanufacturing. Fontainebleau: INSEAD.
Ferrer, G., & Swaminathan, J. M. (2006). Managing new and remanufactured products. Management Science,52(1), 15–26.
Geyer, R., Van Wassenhove, L. N., & Atasu, A. (2007). The economics of remanufacturing under limited component durability and finite product life cycles. Management Science,53(1), 88–100.
Gui, L., Atasu, A., Ergun, Ö., & Toktay, L. B. (2015). Efficient implementation of collective extended producer responsibility legislation. Management Science,62(4), 1098–1123.
Han, X., Wu, H., Yang, Q., & Shang, J. (2016). Reverse channel selection under remanufacturing risks: Balancing profitability and robustness. International Journal of Production Economics,182, 63–72.
Han, X., Yang, Q., Shang, J., & Pu, X. (2017). Optimal strategies for trade-old-for-remanufactured programs: Receptivity, durability, and subsidy. International Journal of Production Economics,193, 602–616.
Hauser, W., & Lund, R. T. (2003). The remanufacturing industry: Anatomy of a giant. Boston: Boston University.
Heese, H. S., Cattani, K., Ferrer, G., Gilland, W., & Roth, A. V. (2005). Competitive advantage through take-back of used products. European Journal of Operational Research,164(1), 143–157.
Huisman, J., Boks, C. B., & Stevels, A. L. N. (2003). Quotes for environmentally weighted recyclability (QWERTY): Concept of describing product recyclability in terms of environmental value. International Journal of Production Research,41(16), 3649–3665.
Liu, H., Lei, M., Deng, H., Leong, G. K., & Huang, T. (2016). A dual channel, quality-based price competition model for the WEEE recycling market with government subsidy. Omega,59, 290–302.
Liu, Z., Tang, J., Li, B. Y., & Wang, Z. (2017). Trade-off between remanufacturing and recycling of WEEE and the environmental implication under the chinese fund policy. Journal of Cleaner Production,167, 97–109.
Ma, W. M., Zhao, Z., & Ke, H. (2013). Dual-channel closed-loop supply chain with government consumption-subsidy. European Journal of Operational Research,226(2), 221–227.
Majumder, P., & Groenevelt, H. (2001). Competition in remanufacturing. Production and Operations Management,10(2), 125–141.
Mitra, S., & Webster, S. (2008). Competition in remanufacturing and the effects of government subsidies. International Journal of Production Economics,111(2), 287–298.
Ongondo, F. O., & Williams, I. D. (2011). Mobile phone collection, reuse and recycling in the UK. Waste Management,31(6), 1307–1315.
Plambeck, E., & Wang, Q. (2009). Effects of e-waste regulation on new product introduction. Management Science,55(3), 333–347.
Saphores, J. D. M., Ogunseitan, O. A., & Shapiro, A. A. (2012). Willingness to engage in a pro-environmental behavior: An analysis of e-waste recycling based on a national survey of US households. Resources, Conservation and Recycling,60, 49–63.
Savaskan, R. C., Bhattacharya, S., & Van Wassenhove, L. N. (2004). Closed-loop supply chain models with product remanufacturing. Management Science,50(2), 239–252.
United States International Trade Commission. (2012). Remanufactured goods: An overview of the US and global industries, markets, and trade. USITC Publication,4356, 332–525.
Vasudevan, H., Kalamkar, V., & Terkar, R. (2012). Remanufacturing for sustainable development: Key challenges, elements, and benefits. International Journal of Innovation, Management and Technology,3(1), 84.
Walls, M., & Palmer, K. (2001). Upstream pollution, downstream waste disposal, and the design of comprehensive environmental policies. Journal of Environmental Economics and Management,41(1), 94–108.
Wu, C. H. (2012). Product-design and pricing strategies with remanufacturing. European Journal of Operational Research,222(2), 204–215.
Zhao, S., & Zhu, Q. (2017). Remanufacturing supply chain coordination under the stochastic remanufacturability rate and the random demand. Annals of Operations Research,257(1–2), 661–695.
Acknowledgements
The work was partly supported by programs granted by the National Natural Science Foundation of China (NSFC) (Nos. 71571051 and 71571115) and the National Natural Science Foundation of Guangdong Province (No. 2015A030313492). The authors cordially thank the editor and two anonymous referee for their helpful comments and suggestions, which significantly helped to improve our paper.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Proof of Theorem 1
It can be verified that \( \Pi^{R} \) is strictly concave in \( q_{n}^{R} \), \( q_{r}^{R} \), and \( q_{d}^{R} \). The Lagrangian and the Karush–Kuhn–Tucker optimality conditions of model R are:
According to the Karush–Kuhn–Tucker condition method, we can derive four optimal strategies, which are characterized as follows.
Case NR (\( \lambda_{1} = 0 \), \( \lambda_{2} > 0 \), and \( \lambda_{3} > 0 \)):
When \( \lambda_{2} > 0 \), and \( \lambda_{3} > 0 \), we can have \( q_{r}^{R} = 0 \), and \( q_{d}^{R} = 0 \), respectively. Therefore, from Eq. (A.1), we can obtain
Substituting them into the linear inverse demand functions in model R, we have:
The values of \( \lambda_{2} \) and \( \lambda_{3} \) must be positive, and the first constraint of model R must be nonnegative, leading to the necessary condition in this case: \( \Delta < c(1 - \alpha ). \)
Case RM (\( \lambda_{1} = 0 \), \( \lambda_{2} > 0 \), and \( \lambda_{3} = 0 \)):
Based on Eqs. (A.1)–(A.3) and (A.7), we can derive:
Substituting them into the linear inverse demand functions in model R, we obtain:
The value of \( \lambda_{2} \) must be positive, and the first and third constraints of model R must be nonnegative, which leads to the necessary condition in this case: \( c(1 - \alpha ) \le \Delta < \frac{b}{{t^{2} }} + c(1 - \alpha ). \)
Case RMP (\( \lambda_{1} = 0 \), \( \lambda_{2} = 0 \), and \( \lambda_{3} = 0 \)):
From Eqs. (A.1)–(A.3), we can obtain: \( q_{n}^{R*} = \frac{{b + Qt(1 - \alpha ) - t^{2} \Delta }}{2t(1 - \alpha )} \), \( q_{d}^{R*} = \frac{b\beta + t((1 - \alpha )(ct\beta + b) - t\beta \Delta )}{2t(1 - \alpha )\alpha \beta }\quad {\text{and}}\quad q_{r}^{R*} = \frac{{t^{2} (\Delta - c(1 - \alpha )) - b}}{2t(1 - \alpha )\alpha }. \)
Substituting optimal prices into the linear inverse demand functions in model R, we have:
In this case, the constraints in model R must be nonnegative; thus, the necessary condition for this case is: \( \frac{b}{{t^{2} }} + c(1 - \alpha ) \le \Delta < \frac{{b\alpha (1 - \alpha ) + (b + ct^{2} (1 - \alpha ))\beta }}{{\beta t^{2} }}. \).
Case RP (\( \lambda_{1} = 0 \), \( \lambda_{2} = 0 \), and \( \lambda_{3} > 0 \)):
From Eqs. (A.1)–(A.3) and (A.8), we can obtain:
Substituting optimal prices into the linear inverse demand functions in model R, we have:
The value of \( \lambda_{3} \) must be positive, and the first and second constraints of model R must be nonnegative, leading to the necessary condition in this case \( \Delta \ge \frac{{b\alpha (1 - \alpha ) + (b + ct^{2} (1 - \alpha ))\beta }}{{\beta t^{2} }}. \)
The proof of model RS is similar to that of model R, and thus omitted here. We provide optimal decisions and outcomes of models R and RS in Tables 2 and 3, respectively. □
1.2 Proof of Corollary 1
We explore the monotonicity of threshold interval lengths by using partial differentiation techniques. For example, taking the first-order partial derivatives of \( \bar{\Delta }_{2} - \bar{\Delta }_{1} \) with respect to \( t \), we have \( \frac{{\partial (\bar{\Delta }_{2} - \bar{\Delta }_{1} )}}{\partial t} = - \frac{2b}{{t^{3} }} \). Therefore, \( \bar{\Delta }_{2} - \bar{\Delta }_{1} \) decreases with \( t \). All the first-order partial derivatives of threshold interval lengths are given in Table 4. According to these results of first-order partial derivatives, we can reach the findings in Corollary 1. □
1.3 Proof of Proposition 2
We use partial differentiation techniques to examine the sensitivities of optimal solutions to product quality level \( t \). The proof is similar to the proof of Corollary 1, and thus omitted here. □
1.4 Proof of Corollary 2
Substituting optimal solutions under strategy NR into the profit function in model R, we have \( \Pi^{NR} = \frac{{(Q - ct)^{2} t}}{4} \). It can be verified that \( \Pi^{NR} \) is strictly concave in \( t \). By solving the first-order condition \( \frac{{\partial \Pi^{NR} }}{\partial t} = 0 \), we can have the optimal product quality level is \( \bar{t}_{NR}^{*} = Q/3c \). Similarly, we can derive the optimal product quality level under strategy RM is \( \bar{t}_{RM}^{*} = Q/3c. \)
Substituting optimal solutions under strategy RMP into the profit function in model R, we have
It can be verified that \( \Pi^{R} \) is strictly concave in \( t \), because \( \frac{{\partial^{2} \Pi^{R} }}{{\partial t^{2} }} > 0 \). Taking the first-order partial derivatives of \( \Pi^{R} \) with respect to \( t \), we can have \( \frac{{\partial \Pi^{R} }}{\partial t} = \frac{Q\alpha (Q - 2ct)}{4} + \frac{R}{{4\alpha t^{2} (1 - \alpha )}} \), where \( R = 3t^{4} (1 - \alpha )((2c - 1)\Delta + (1 - \alpha )c^{2} ) + b(2t^{2} (\Delta - c(1 - \alpha )) + b) > 0 \). Therefore, we have \( \bar{t}_{RMP} > \frac{Q}{2c} > \bar{t}_{RM} = \bar{t}_{NR} \). Similarly, we can have \( \frac{{\partial \Pi^{R} }}{\partial t} = Q(Q - 2ct) + \frac{T}{{4(\alpha t(1 - \alpha ) + \beta )^{3} }} \), where
Therefore, we can derive that \( \bar{t}_{RP} > \bar{t}_{RMP} > \bar{t}_{RM} = \bar{t}_{NR} . \) □
1.5 Proof of Proposition 3
We use partial differentiation techniques to investigate the sensitivities of optimal solutions to government subsidy \( s \). The proof is similar to the proof of Corollary 1, and thus omitted here. □
1.6 Proof of Proposition 4
According to Eqs. (5), (6), we can derive \( CS^{R} = \frac{1}{8t(Q - ct)^{2}} \), and \( CS^{RS} = \frac{1}{8t(Q - ct)^{2}} \) under RM, we can derive \( CS^{R} = \frac{{t(b^{2} + t^{2} (1 - \alpha )(c^{2} t^{2} + (Q - 2)(Q - 2 + 2ct)\alpha ) + 2ct^{4} (1 - \alpha )\Delta + t^{4} \Delta^{2} + 2bt^{2} (c(1 - \alpha ) + \Delta ))}}{8t(1 - \alpha )\alpha } \), and \( CS^{RS} = \frac{{t(b^{2} + t^{2} (1 - \alpha )(c^{2} t^{2} + (Q - 2)(Q - 2 + 2ct)\alpha ) + 2ct^{4} (1 - \alpha )\Delta + t^{4} \Delta^{2} + 2bt^{2} (c(1 - \alpha ) + \Delta ))}}{8t(1 - \alpha )\alpha } \) under RMP, respectively. By comparing the values of \( CS^{R} \) and \( CS^{RS} \), we can obtain \( CS^{R} = CS^{RS} \) under RM and RMP. Thus, the proof of Proposition 4a is completed. Similarly, we can easily prove Proposition 4b, c. □
1.7 Proof of Proposition 5
According to Eq. (7), we can derive \( RR^{R} = \frac{b}{(Q - ct)t\beta } \) and \( RR^{RS} = \frac{b + s}{(Q - ct)t\beta } \) under RM. By comparing the values of \( RR^{R} \) and \( RR^{RS} \), we can find \( RR^{R} < RR^{RS} \). Similarly, based on Eqs. (10), (11), we can derive \( H^{NR} = \frac{{e_{d} (Q - ct)}}{2} \) under NR, and \( H^{R} = \frac{{e_{d} ((Q - ct)\beta - b)}}{2\beta } \), \( H^{RS} = \frac{{e_{d} ((Q - ct)\beta - b - s)}}{2\beta } \) under RM, respectively. By comparing the values of \( H^{NR} \), \( H^{R} \) and \( H^{RS} \), we can find \( H^{R} > H^{RS} \). Similarly, we can have \( RR^{R} < RR^{RS} \) and \( H^{R} > H^{RS} \) under RMP and RP. Thus, we can obtain Proposition 5a.
Substituting optimal quantities into \( RR \) under NR, RM, RMP and RP, respectively, we can obtain \( RR_{NR} = 0 \), \( RR_{RM} = \frac{b}{(Q - ct)t\beta } \), \( RR_{RMP} = \frac{bt(1 - \alpha )}{\beta (b + t(Q + Q\alpha - \Delta t))} \), and \( RR_{RP} = \frac{{t^{2} (\Delta - c(1 - \alpha ))}}{Q(t\alpha (1 - \alpha ) + \beta ) - t(c\beta + t\alpha \Delta )} \), respectively. Taking the first-order partial derivatives of \( RR_{RM} \), \( RR_{RMP} \), \( RR_{RP} \) with respect to \( \Delta \), respectively, we have \( \frac{{\partial RR_{RM} }}{\partial \Delta } = 0 \),\( \frac{{\partial RR_{RMP} }}{\partial \Delta } = \frac{{bt^{3} (1 - \alpha )}}{{\beta (b + t(Q + Q\alpha - \Delta t))^{2} }} > 0 \), \( \frac{{\partial RR_{RP} }}{\partial \Delta } = \frac{{t^{2} (t\alpha (Q + ct)(1 - \alpha ) + \beta (Q - ct))}}{{(Q(t\alpha (1 - \alpha ) + \beta ) - t(c\beta + t\alpha \Delta ))^{2} }} > 0 \). Therefore, \( RR_{RM} \) is independent of \( \Delta \), but \( RR_{RMP} \) and \( RR_{RP} \) increase with \( \Delta \). Substituting \( \bar{\Delta }_{1} \) and \( \bar{\Delta }_{2} \) into \( RR \) under RM, we can obtain \( RR_{{RM/\bar{\Delta }_{1} }} = \frac{b}{(Q - ct)t\beta } \) and \( RR_{{RMP/\bar{\Delta }_{2} }} = \frac{b}{(Q - ct)t\beta } \). Similarly, we can obtain \( RR_{{RMP/\bar{\Delta }_{2} }} = \frac{b}{(Q - ct)t\beta } \), \( RR_{{RMP/\bar{\Delta }_{3} }} = \frac{b}{(Q - ct)t\beta - b\alpha } \) and \( RR_{{RP/\bar{\Delta }_{3} }} = \frac{b}{(Q - ct)t\beta - b\alpha } \).
Thus, we have \( RR_{RM} = \frac{b}{(Q - ct)\beta } \) when \( \bar{\Delta }_{1} \le \Delta < \bar{\Delta }_{2} \); \( \frac{b}{(Q - ct)t\beta } \le RR_{RMP} < \frac{b}{(Q - ct)t\beta - b\alpha } \) when \( \bar{\Delta }_{2} \le \Delta < \bar{\Delta }_{3} \) and \( \frac{b}{(Q - ct)t\beta - b\alpha } \le RR_{RP} \) when \( \bar{\Delta }_{3} \le \Delta \). By comparing the values of \( RR_{NR} \), \( RR_{RMP} \), \( RR_{RM} \) and \( RR_{RP} \), we have \( RR_{NR} < RR_{RM} \le RR_{RMP} < RR_{RP} \). Using the same techniques, we can obtain \( H_{NR} > H_{RM} \ge H_{RMP} > H_{RP} \). Thus, we can prove Proposition 5b. □
Rights and permissions
About this article
Cite this article
Han, X., Shen, Y. & Bian, Y. Optimal recovery strategy of manufacturers: Remanufacturing products or recycling materials?. Ann Oper Res 290, 463–489 (2020). https://doi.org/10.1007/s10479-018-2929-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-018-2929-5