Normal compression wave scattering by a permeable crack in a fluid-saturated poroelastic solid

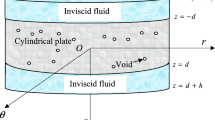
Abstract

A mathematical formulation is presented for the dynamic stress intensity factor (mode I) of a finite permeable crack subjected to a time-harmonic propagating longitudinal wave in an infinite poroelastic solid. In particular, the effect of the wave-induced fluid flow due to the presence of a liquid-saturated crack on the dynamic stress intensity factor is analyzed. Fourier sine and cosine integral transforms in conjunction with Helmholtz potential theory are used to formulate the mixed boundary-value problem as dual integral equations in the frequency domain. The dual integral equations are reduced to a Fredholm integral equation of the second kind. It is found that the stress intensity factor monotonically decreases with increasing frequency, decreasing the fastest when the crack width and the slow wave wavelength are of the same order. The characteristic frequency at which the stress intensity factor decays the fastest shifts to higher frequency values when the crack width decreases.

Appendices

Appendix A: Details of theoretical derivations

1.1 Part 1: Solution of the dual integral equations (58) and (59)

To solve the dual integral equations (58) and (59), Eq. (59) is integrated with respect x over the interval $\left( {0,x} \right)$. The results for the pair of the dual integral equations are summarized as follows

$$\begin{aligned}&\int \nolimits _0^\infty {\hat{{B}}\left( k \right) \cos \left( {kx} \right) \hbox {d}k} =0,\quad x>a, \nonumber \\&\int \nolimits _0^\infty {\left[ {1+H\left( k \right) } \right] \hat{{B}}\left( k \right) \sin \left( {kx} \right) \hbox {d}k} =-xf\left( \omega \right) ,\nonumber \\&\quad 0\le x\le a. \end{aligned}$$

(A1)

According to the Fourier cosine transform, a displacement related function $B\left( x \right)$ can be defined by

$$\begin{aligned} B\left( x \right) =\frac{2}{{\uppi }}\int \nolimits _0^\infty {\hat{{B}}\left( k \right) \cos \left( {kx} \right) \hbox {d}k}, \end{aligned}$$

(A2)

where $B\left( x \right)$ must be zero for $x>a$ as required by Eq. (A1). Hence, the Fourier inversion theorem leads to the expression,

$$\begin{aligned} \hat{{B}}\left( k \right) =\int \nolimits _0^a {B\left( x \right) \cos \left( {kx} \right) \hbox {d}x}. \end{aligned}$$

(A3)

For the mode I crack problem, the normal stress possesses a square-root singularity near the tip of a plane strain crack. To obtain the solution of this pair, we set

$$\begin{aligned} B\left( x \right) =\int \nolimits _x^a {\frac{\lambda \left( \tau \right) \tau }{\sqrt{\tau ^{2}-x^{2}}}\hbox {d}\tau },\quad 0\le x\le a, \end{aligned}$$

(A4)

where the function $\lambda \left( \tau \right)$ is required to be continuous on the interval $\left[ {0, a} \right]$. Substitution of Eq. (A4) into Eq. (A3), change of the order of integration, and application of the identity [21]

$$\begin{aligned} \int \nolimits _0^\tau {\frac{\cos \left( {kx} \right) }{\sqrt{\tau ^{2}-x^{2}}}\hbox {d}x} =\frac{{\uppi }}{2}J_0 \left( {k\tau } \right) , \end{aligned}$$

(A5)

where $J_0$ is the zero-order Bessel function of the first kind, leads to the expression

$$\begin{aligned} \hat{{B}}\left( k \right) =\frac{{\uppi }}{2}\int \nolimits _0^a {\lambda \left( \tau \right) \tau J_0 \left( {k\tau } \right) \hbox {d}\tau }. \end{aligned}$$

(A6)

Substitution Eq. (A6) into the second equation of Eq. (A1), change of the order of integration, and application of the relation [21]

$$\begin{aligned} \int \nolimits _0^\infty {J_0 \left( {k\tau } \right) \sin \left( {kx} \right) \hbox {d}k} =\left\{ {\begin{array}{ll} 0, &{}\quad 0<x<\tau , \\ \frac{1}{\sqrt{x^{2}-\tau ^{2}}}, &{}\quad 0<\tau <x \\ \end{array}} \right. \end{aligned}$$

(A7)

renders the following Abel’s integral equation [22]

$$\begin{aligned} \int \nolimits _0^x {\frac{\lambda \left( \tau \right) \tau }{\sqrt{x^{2}-\tau ^{2}}}\hbox {d}\tau } =\beta \left( x \right) ,\quad 0\le x\le a, \end{aligned}$$

(A8)

where

$$\begin{aligned} \beta \left( x \right)= & {} -\frac{2}{{\uppi }}xf\left( \omega \right) -\int \nolimits _0^\infty H\left( k \right) \nonumber \\&\left[ {\int \nolimits _0^a {\lambda \left( \tau \right) \tau J_0 \left( {k\tau } \right) \hbox {d}\tau } } \right] \sin \left( {kx} \right) \hbox {d}k. \end{aligned}$$

(A9)

The solution of the Abel’s integral equation is (see Refs. [6, 7])

$$\begin{aligned} \lambda \left( \tau \right) =\frac{2}{{\uppi }}\int \nolimits _0^\tau {\frac{{\beta }^{\prime }\left( x \right) }{\sqrt{\tau ^{2}-x^{2}}}\hbox {d}x} ,\quad 0\le \tau \le a, \end{aligned}$$

(A10)

where ${\beta }^{\prime }\left( x \right)$ denotes the derivative of $\beta \left( x \right)$.

Substitution of Eq. (A9) into Eq. (A10), change of the order of integration, and application of Eq. (A5) yields a Fredholm integral equation of the second kind

$$\begin{aligned}&\lambda \left( \tau \right) +\int \nolimits _0^a {\lambda \left( {{\tau }^{\prime }} \right) {\tau }^{\prime }\left[ {\int \nolimits _0^\infty {H\left( k \right) kJ_0 \left( {k\tau } \right) J_0 \left( {k{\tau }^{\prime }} \right) \hbox {d}k} } \right] \hbox {d}{\tau }^{\prime }} \nonumber \\&\quad =-\frac{2}{{\uppi }}f\left( \omega \right) ,\quad 0\le \tau \le a. \end{aligned}$$

(A11)

To obtain the coefficient $\hat{{B}}\left( k \right)$, we multiply both sides of Eq. (A11) by $\frac{{\uppi }}{2}J_0 \left( {k\tau } \right) \tau$ and integrate the resulting equation with respect to $\tau$ from $\tau =0$ to $\tau =a$. Change of the order of integration and use of identities [21]

$$\begin{aligned}&\int \nolimits _0^a {\tau J_0 \left( {{k}^{\prime }\tau } \right) J_0 \left( {k\tau } \right) \hbox {d}\tau } \nonumber \\&\quad =\frac{{k}^{\prime }aJ_{-1} \left( {{k}^{\prime }a} \right) J_0 \left( {ka} \right) -kaJ_{-1} \left( {ka} \right) J_0 \left( {{k}^{\prime }a} \right) }{k^{2}-{k}^{\prime 2}}, \nonumber \\&\int \nolimits _0^a {\tau J_0 \left( {k\tau } \right) \hbox {d}\tau } =\frac{aJ_1 \left( {ka} \right) }{k} \end{aligned}$$

(A12)

lead to a new Fredholm equation

$$\begin{aligned}&\hat{{B}}\left( k \right) +\int \nolimits _0^\infty {K_{\hat{{B}}} \left( {k,{k}^{\prime }} \right) \hat{{B}}\left( {{k}^{\prime }} \right) \hbox {d}{k}^{\prime }} =-f\left( \omega \right) ak^{-1}J_1 \left( {ka} \right) \nonumber \\ \end{aligned}$$

(A13)

with the kernel function

$$\begin{aligned} K_{\hat{{B}}} \left( {k,{k}^{\prime }} \right)= & {} {k}^{\prime }aH\left( {{k}^{\prime }} \right) \nonumber \\&\times \left[ {\frac{{k}^{\prime }J_{-1} \left( {{k}^{\prime }a} \right) J_0 \left( {ka} \right) -kJ_{-1} \left( {ka} \right) J_0 \left( {{k}^{\prime }a} \right) }{k^{2}-{k}^{\prime 2}}} \right] ,\nonumber \\ \end{aligned}$$

(A14)

where $J_n$ is the n-order Bessel function of the first kind.

Now introduce a function $\varphi \left( x \right) =-\sqrt{x}\lambda \left( x \right)$ such that it is governed by the following Fredholm equation

$$\begin{aligned}&\varphi \left( x \right) +\int \nolimits _0^a {K_\varphi \left( {x,{x}^{\prime }} \right) \varphi \left( {{x}^{\prime }} \right) \hbox {d}{x}^{\prime }}=\frac{2}{{\uppi }}\sqrt{x}f\left( \omega \right) ,\quad 0\le x\le a,\nonumber \\ \end{aligned}$$

(A15)

whose kernel, being symmetric in x and ${x}^{\prime }$, is

$$\begin{aligned} K_\varphi \left( {x,{x}^{\prime }} \right) =\sqrt{x{x}^{\prime }}\int \nolimits _0^\infty {H\left( k \right) kJ_0 \left( {kx} \right) J_0 \left( {k{x}^{\prime }} \right) \hbox {d}k} . \end{aligned}$$

(A16)

As is shown in the next part, the function $\varphi \left( a \right)$ is related to the dynamic stress intensity factor. The integral (A16) cannot be expressed in terms of tabulated functions. However, it can be simplified and written in a form more suitable for numerical evaluation. The method is to extend the integrand into the complex half-plane $\hbox {Re}\left( k \right) \ge 0$ and use contour integration to reduce the integral to a finite range. Details of the procedure are given in “Appendix B”.

1.2 Part 2: Stress intensity factor

The function $\hat{{B}}\left( k \right)$ given by Eq. (A6) can be expressed in terms of $\varphi \left( x \right)$ as

$$\begin{aligned} \hat{{B}}\left( k \right) =-\frac{{\uppi }}{2}\int \nolimits _0^a {\sqrt{x}\varphi \left( x \right) J_0 \left( {kx} \right) \hbox {d}x}. \end{aligned}$$

(A17)

Integrate the function $\hat{{B}}\left( k \right)$ in Eq. (A17) by parts, and retain the term contributing to the singular behavior of the stress component at the crack tip, we obtain

$$\begin{aligned} \hat{{B}}\left( k \right) =-\frac{{\uppi }}{2k}\varphi \left( a \right) \sqrt{a}J_1 \left( {ka} \right) +\cdots . \end{aligned}$$

(A18)

Substituting Eq. (A18) into Eq. (62) yields

$$\begin{aligned} \sigma _{yy}^{(s)} \left( {x,0} \right)= & {} -\varphi \left( a \right) \sqrt{a}\int \nolimits _0^\infty h\left( k \right) J_1 \left( {ka} \right) \nonumber \\&\cos \left( {kx} \right) \hbox {d}k+\cdots ,\quad x>a. \end{aligned}$$

(A19)

Now, we rewrite the integral in Eq. (A19) in equivalent form

$$\begin{aligned}&\int \nolimits _0^\infty {h\left( k \right) J_1 \left( {ka} \right) \cos \left( {kx} \right) } \hbox {d}k\nonumber \\&\quad =\int \nolimits _0^\infty {h^{\infty }J_1 \left( {ka} \right) \cos \left( {kx} \right) } \hbox {d}k \nonumber \\&\qquad +\int \nolimits _0^\infty {\left[ {h\left( k \right) -h^{\infty }} \right] J_1 \left( {ka} \right) \cos \left( {kx} \right) } \hbox {d}k, \end{aligned}$$

(A20)

where

$$\begin{aligned} h^{\infty }= & {} \frac{\uppi }{E}\sum _{i=1}^2 \left[ \left( {\chi _2 -\chi _3 } \right) \left( {H-\mu +C\chi _1 } \right) k_1^2\right. \nonumber \\&\left. +\left( {\chi _3 -\chi _1 } \right) \left( {H-\mu +C\chi _2 } \right) k_2^2 \right] \end{aligned}$$

(A21)

denotes $\mathop {\lim }\nolimits _{k\rightarrow \infty } h\left( k \right)$. Evidently, the second integral on the right hand of Eq. (A20) is finite, while the first integral gives rise to stress singularity at $x=a^{+}$. Therefore, we may write the total normal stress as

$$\begin{aligned} \sigma _{yy} \left( {x,0} \right)= & {} -\varphi \left( a \right) \sqrt{a}h^{\infty }\int \nolimits _0^\infty {J_1 \left( {ka} \right) \cos \left( {kx} \right) } \hbox {d}k\nonumber \\&+\,\hbox {non-singular terms,}\quad x>a. \end{aligned}$$

(A22)

Fig. 6

Integration contours (arrowed solid lines) and branch cuts (dotted lines) in the complex k-plane. The left panel $H_0^{(1)} \left( {k{x}^{\prime }} \right)$-contour, the right panel $H_0^{(2)} \left( {k{x}^{\prime }} \right)$-contour

Next, using the equation [21]

$$\begin{aligned}&\int \nolimits _0^\infty {J_1 \left( {ka} \right) \cos \left( {kx} \right) } \hbox {d}k=\frac{-a}{\sqrt{x^{2}-a^{2}}\left( {x+\sqrt{x^{2}-a^{2}}} \right) },\quad x>a, \nonumber \\ \end{aligned}$$

(A23)

we obtain

$$\begin{aligned} \sigma _{yy} \left( {x,0} \right)= & {} \frac{\varphi \left( a \right) a\sqrt{a}h^{\infty }}{\sqrt{x^{2}-a^{2}}\left( {x+\sqrt{x^{2}-a^{2}}} \right) }\nonumber \\&+\hbox {non-singular terms,}\quad x>a. \end{aligned}$$

(A24)

Now, inserting Eq. (A24) into Eq. (61) yields

$$\begin{aligned} K_1 =\varphi \left( a \right) h^{\infty }. \end{aligned}$$

(A25)

Appendix B: Manipulation of the kernel $K_\varphi \left( {x,{x}^{\prime }} \right)$

The purpose of this appendix is to reformulate the integral $K_\varphi \left( {x,{x}^{\prime }} \right)$ given by Eq. (A16) to a finite range. This can be accomplished by using the method of contour integration. The procedure is to choose the branch cuts consistently with the restriction (37) and then extend the integrand into the complex half-plane $\hbox {Re}\left( k \right) \ge 0$. The derivation follows the method given by Song et al. [9] who treat an 3D elastic wave scattering problem by a permeable penny-shaped crack in a poroelastic medium. Here we give some details of the manipulation of the integral (A16).

Because of the symmetry $K_\varphi \left( {x,{x}^{\prime }} \right) =K_\varphi \left( {{x}^{\prime },x} \right)$ it is no restriction to impose the condition ${x}^{\prime }\ge x$. The principle in the contour integration used here to reformulate the kernel $K_\varphi \left( {x,{x}^{\prime }} \right)$ is to write one of the Bessel functions in the integrand as the sum of Hankel functions:

$$\begin{aligned} J_0 \left( {k{x}^{\prime }} \right) =\frac{1}{2}\left[ {H_0^{(1)} \left( {k{x}^{\prime }} \right) +H_0^{(2)} \left( {k{x}^{\prime }} \right) } \right] . \end{aligned}$$

(B1)

In anticipation of a special convergence problem the integral (A16) is expressed by the limit

$$\begin{aligned} K_\varphi \left( {x,{x}^{\prime }} \right)= & {} \frac{\sqrt{x{x}^{\prime }}}{2}\mathop {\lim }\limits _{\delta \rightarrow 0^{+}} \int \nolimits _\delta ^\infty H\left( k \right) kJ_0 \left( {kx} \right) \nonumber \\&\left[ {H_0^{(1)} \left( {k{x}^{\prime }} \right) +H_0^{(2)} \left( {k{x}^{\prime }} \right) } \right] \hbox {d}k. \end{aligned}$$

(B2)

The integral is, therefore, separated into two parts, one containing $\hbox {e}^{\mathrm{i}k{r}^{\prime }}$ and the other containing $\hbox {e}^{-\mathrm{i}k{r}^{\prime }}$. The function $H\left( k \right)$ given by Eq. (60) associated with Eq. (55) is repeated here for convenience in an equivalent way:

$$\begin{aligned} H\left( k \right)= & {} \frac{4\mu }{Ek}\left[ {\left( {\chi _3 -\chi _2 } \right) \left( {k^{2}-\sigma _1 k_1^2 } \right) \left( {k^{2}-\sigma _3 k_1^2 } \right) \eta _1^{-1} } \right. \nonumber \\&{+}\left( {\chi _1 -\chi _3 } \right) \left( {k^{2}-\sigma _2 k_2^2 } \right) \left( {k^{2}-\sigma _4 k_2^2 } \right) \eta _2^{-1} \nonumber \\&\left. -\left( {\chi _1 -\chi _2 } \right) k^{2}\eta _3 \right] -1. \end{aligned}$$

(B3)

where $\sigma _1$, $\sigma _2$, $\sigma _3$, $\sigma _4$, and E are given by Eqs. (51), (53), and (57).

Consider the function $H\left( k \right)$ in the complex plane for a given frequency, $\pm k_i\ \left( {i=1,2,3} \right)$ are branch points of the multivalued function $H\left( k \right)$. To accomplish the integrals (B2), we adopt the branch cuts and integration contours shown in Fig. 6. The first term which containing $H_0^{(1)} \left( {k{x}^{\prime }} \right)$ is integrated along the closed contour in the left panel, while the second containing $H_0^{(2)} \left( {k{x}^{\prime }} \right)$ is integrated along the contour in the right panel. As neither of the integrands contains any poles within the closed contours, the original integrals in Eq. (B2) with the restriction (37) can be replaced by integrals over the remainder of the contours, taken in the opposite direction.

For large or small values of $\left| \xi \right|$ the asymptotic behavior of the Bessel functions is [23]

$$\begin{aligned}&\left. {\begin{array}{l} J_0 \left( \xi \right) \sim \sqrt{\frac{2}{{\uppi }\xi }}\cos \left( {\xi -\frac{{\uppi }}{4}} \right) \\ H_0^{(1)} \left( \xi \right) \sim \sqrt{\frac{2}{{\uppi }\xi }}\hbox {e}^{\mathrm{i}\left( {\xi -\frac{{\uppi }}{4}} \right) } \\ H_0^{(1)} \left( \xi \right) \sim \sqrt{\frac{2}{{\uppi }\xi }}\hbox {e}^{-\mathrm{i}\left( {\xi -\frac{{\uppi }}{4}} \right) } \\ \end{array}} \right\} \quad \left| \xi \right| \rightarrow \infty , \end{aligned}$$

(B4)

$$\begin{aligned}&\left. {\begin{array}{l} J_0 \left( \xi \right) \sim 1 \\ H_0^{(1)} \left( \xi \right) \sim \mathrm{i}\frac{2}{{\uppi }}\ln \frac{\xi }{2} \\ H_0^{(1)} \left( \xi \right) \sim -\mathrm{i}\frac{2}{{\uppi }}\ln \frac{\xi }{2} \\ \end{array}} \right\} \quad \left| \xi \right| \rightarrow 0. \end{aligned}$$

(B5)

With the definition in Eq. (B3) of $H\left( k \right)$, it is seen that $H\left( k \right) {\sim }k^{-2}$ as $\left| k \right| \rightarrow \infty$. The part of the integrand containing $H_0^{(1)} \left( {k{x}^{\prime }} \right)$ therefore behaves asymptotically like $\left| k \right| ^{-2}$ in the upper half-plane, while that containing $H_0^{(2)} \left( {k{x}^{\prime }} \right)$ behaves asymptotically like $\left| k \right| ^{-2}$ in the lower half-plane. According to Jordan’s lemma the integrals along the large quarter circles do not contribute.

The integration along the arcs around the coordinate origin O depends on the asymptotic behavior of the integrands as $k\rightarrow 0$. The functions $H\left( k \right) k^{2}J_0 \left( {kx} \right) H_0^{(1, 2)} \left( {k{x}^{\prime }} \right)$ tend to zero as $k\rightarrow 0$ so that the integrals along the arcs around the point O do not contribute either.

Furthermore, the contributions from the imaginary axis cancel resulting from the symmetry relation [24]

$$\begin{aligned} -kJ_0 \left( {-kx} \right) H_0^{(1)} \left( {-k{x}^{\prime }} \right) =kJ_0 \left( {kx} \right) H_0^{(2)} \left( {k{x}^{\prime }} \right) . \end{aligned}$$

(B6)

The function $\left( {k-k_i } \right) H\left( k \right) kJ_0 \left( {kx} \right) H_0^{(1)} \left( {k{x}^{\prime }} \right)$ tends to zero as $k\rightarrow k_i$. Thus, there is no contribution from small circles wrapping around branch points.

Now collection of the integration along the branch cuts leads to the expression that is more compact and amenable to numerical evaluation

$$\begin{aligned} \frac{K_\varphi \left( {x,{x}^{\prime }} \right) }{4\mathrm{i}\mu }= & {} \frac{\sqrt{x{x}^{\prime }}}{E}\left[ \left( {\chi _3 -\chi _2 } \right) k_1^4 \int \nolimits _0^1 {\left( {\xi ^{2}-\sigma _1 } \right) \left( {\xi ^{2}-\sigma _3 } \right) } \right. \nonumber \\&\times \frac{J_0 \left( {k_1 x\xi } \right) H_0^{(1)} \left( {k_1 {x}^{\prime }\xi } \right) }{\sqrt{1-\xi ^{2}}}\hbox {d}\xi \nonumber \\&+\left( {\chi _1 -\chi _3 } \right) k_2^4 \int \nolimits _0^1 \left( {\xi ^{2}-\sigma _2 } \right) \left( {\xi ^{2}-\sigma _4 } \right) \nonumber \\&\times \frac{J_0 \left( {k_2 x\xi } \right) H_0^{(1)} \left( {k_2 {x}^{\prime }\xi } \right) }{\sqrt{1-\xi ^{2}}} \hbox {d}\xi \nonumber \\&+\left( {\chi _1 -\chi _2 } \right) k_3^4 \int \nolimits _0^1 \xi ^{2}\sqrt{1-\xi ^{2}}J_0 \left( {k_3 x\xi } \right) \nonumber \\&\times \left. H_0^{(1)} \left( {k_3 {x}^{\prime }\xi } \right) \hbox {d}\xi \right] , \end{aligned}$$

(B7)

where $\xi$ is a dimensionless real variable.