Elastoplastic homogenization of particulate composites complying with the Mohr–Coulomb criterion and undergoing isotropic loading

Abstract

This work aims at determining the overall response of a two-phase elastoplastic composite to isotropic loading. The composite under investigation consists of elastic particles embedded in an elastic perfectly plastic matrix governed by the Mohr–Coulomb yield criterion and a non-associated plastic flow rule. The composite sphere assemblage model is adopted, and closed-form estimates are derived for the effective elastoplastic properties of the composite either under tensile or compressive isotropic loading. In the case when elastic particles reduce to voids, the composite in question degenerates into a porous elastoplastic material. The results obtained in the present work are of interest, in particular, for soil mechanics.

Graphical abstract

Appendix

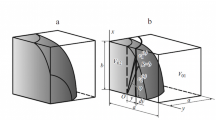
Consider a composite sphere $\varOmega$ made of phase 2 surrounded by a concentric coating consisting of phase 1. Let the outer surface $\partial \varOmega$ of $\varOmega$ be subjected to a monotonous isotropic loading $p_{0}$ starting from zero. Before $p_{0}$ reaches the initial yielding load $p^{\prime }$, both the core and coating remain linearly elastic. The corresponding stress fields in the core and coating can be analytically and explicitly determined as in Ref. [3]. Introducing these results into the M–C yield function of Eq. (5), we obtain the yielding condition:

$$\begin{aligned} f^{(1)}(\varvec{\sigma })\!= & {} \!\frac{p_{0}[\mu _{1}\left( \frac{a}{r}\right) ^{3}(\kappa _{1}\!-\!\kappa _{2})(-\!3\gamma \!-\!\sin \phi )\!+\!\kappa _{1}(4\mu _{1}\!+\!3\kappa _{2})\sin \phi ]}{4\mu _{1}c(\kappa _{1}\!-\!\kappa _{2})\!-\!\kappa _{1}(4\mu _{1}\!+\!3\kappa _{2})}\nonumber \\&-\, C\cos \phi \leqslant 0. \end{aligned}$$

(92)

Let us study the question of whether the above yield condition can be fulfilled when accounting for the tensile and compressive loading modes and considering all values of the internal friction angle $\phi \in (0,\frac{\uppi }{2})$. The following four cases need to be distinguished:

• (1) Tensile loading $p_{0}\leqslant 0$ and $\kappa _{1}>\kappa _{2},$ leading to $\gamma =-1$. Then, we can verify that Eq. (92) is satisfied first at the interface $r=a^{+}$ when $p_{0}=p^{\prime }$.

• (2) Tensile loading $p_{0}\leqslant 0$, but $\kappa _{1}<\kappa _{2},$ giving rise to $\gamma =+1$. The plastification of the matrix takes place first at the interface $r=a^{+}$ when $p_{0}=p^{\prime }$.

• (3) Compressive loading $p_{0}\geqslant 0$ and $\kappa _{1}>\kappa _{2}$. In this case, $\gamma =+1$. The yield condition can hold only when $\sin \phi <(2\delta _{1}+1)^{-1}.$ Otherwise, the two constituent phases will remain elastic for any pressure $p_{0}$.

• (4) Compressive loading $p_{0}\geqslant 0$ but $\kappa _{1}<\kappa _{2}$. Correspondingly, $\gamma =-1.$ The initial plastification can be produced only if $\sin \phi <-(2\delta _{1}+1)^{-1}$.

Once the matrix gets plastified for $p_{0}=p^{\prime }$ and when $p_{0}$ increases, an annular plastic zone expands from the inner coating surface $\rho =a^{+}$ towards the outer coating surface $\rho =b$. At the current pressure $p_{0},$ the non-zero displacement, strain, and stress fields in the two elastic zones can be found in Ref. [3]. For the purpose of comparison, the same notation is used as in Ref. [1]:

• $0\leqslant r\leqslant a,$ the elastic core made of phase 2,

  $$\begin{aligned} u_{r}^{(2)}= & {} a_{2}r,\ \ \varepsilon _{r}^{(2)}=\varepsilon _{\theta }^{(2)}=\varepsilon _{\varphi }^{(2)}=a_{2}, \end{aligned}$$

  (93)
  $$\begin{aligned} \sigma _{r}^{(2)}= & {} \sigma _{\theta }^{(2)}=\sigma _{\varphi }^{(2)}=3\kappa _{2}a_{2}; \end{aligned}$$

  (94)

• $\rho \leqslant r\leqslant b,$ the elastic part of the matrix made of phase 1,

  $$\begin{aligned}&u_{r}^{(1)} =a_{1}r+\frac{b_{1}}{r^{2}},\quad \varepsilon _{r}^{(1)}=a_{1}- \frac{2b_{1}}{r^{3}},\nonumber \\&\varepsilon _{\theta }^{(1)}=\varepsilon _{\varphi }^{(1)}=a_{1}+\frac{b_{1}}{r^{3}},\end{aligned}$$

  (95)
  $$\begin{aligned}&\sigma _{r}^{(1)} =3\kappa _{1}a_{1}-\frac{4\mu _{1}b_{1}}{r^{3}},\nonumber \\&\sigma _{\theta }^{(1)}=\sigma _{\varphi }^{(1)}=3\kappa _{1}a_{1}+\frac{2\mu _{1}b_{1}}{r^{3}}, \end{aligned}$$

  (96)

  where $a_{1},b_{1}$ and $a_{2}$ are constants to be determined by the boundary and interface continuity conditions.

The stress field of the plastic zone in the coating must satisfy the Mohr–Coulomb condition of Eq. (92) and the equilibrium equation

$$\begin{aligned} \frac{\hbox {d}\sigma _{r}^{(1)}}{\hbox {d}r}+\frac{2(\sigma _{r}^{(1)}-\sigma _{\theta }^{(1)})}{r}=0. \end{aligned}$$

(97)

The solution to this equation is given by

$$\begin{aligned} \sigma _{r}^{(1)}= & {} -D\zeta ^{-2q}+C\cot \phi , \end{aligned}$$

(98)

$$\begin{aligned} \sigma _{\theta }^{(1)}= & {} \sigma _{\varphi }^{(1)}=D(q-1)\zeta ^{-2q}+C\cot \phi , \end{aligned}$$

(99)

where $\zeta =r / \rho$ and D is an unknown constant to be determined below. The strain field of the matrix includes an elastic part specified as

$$\begin{aligned} \varepsilon _{\mathrm{e}r}^{(1)}= & {} \frac{\sigma _{r}^{(1)}}{E_{1}}-\frac{2\nu _{1}\sigma _{\theta }^{(1)}}{E_{1}}, \nonumber \\ \varepsilon _{\mathrm{e}\theta }^{(1)}= & {} \varepsilon _{\mathrm{e}\varphi }^{(1)}=\frac{-\nu _{1}\sigma _{r}^{(1)}}{ E_{1}}+\frac{(1-\nu _{1})\sigma _{\theta }^{(1)}}{E_{1}}, \end{aligned}$$

(100)

and a plastic part written in the form

$$\begin{aligned} \varepsilon _{\mathrm{p}r}^{(1)}=\omega \beta _{1}^{\prime },\quad \varepsilon _{\mathrm{p}\theta }^{(1)}=\varepsilon _{\mathrm{p}\varphi }^{(1)}=-\frac{\omega \beta _{2}^{\prime }}{2}, \end{aligned}$$

(101)

where $\beta _{1}^{\prime }$ and $\beta _{2}^{\prime }$ are given in Eq. (28) and $\omega$ represents an unknown scalar function of r. Thus, the strain components of the matrix have the expressions

$$\begin{aligned} \varepsilon _{r}^{(1)}= & {} \frac{\sigma _{r}^{(1)}}{E_{1}}-\frac{2\nu _{1}\sigma _{\theta }^{(1)}}{E_{1}}+\omega \beta _{1}^{\prime }, \end{aligned}$$

(102)

$$\begin{aligned} \varepsilon _{\theta }^{(1)}= & {} \varepsilon _{\varphi }^{(1)}=\frac{-\nu _{1}\sigma _{r}^{(1)}}{E_{1}}+\frac{(1-\nu _{1})\sigma _{\theta }^{(1)}}{ E_{1}}-\frac{\omega \beta _{2}^{\prime }}{2}. \end{aligned}$$

(103)

Substituting the above strain components into the compatibility equation

$$\begin{aligned} \frac{\hbox {d}\varepsilon _{\theta }^{(1)}}{\hbox {d}r}+\frac{\varepsilon _{\theta }^{(1)}-\varepsilon _{r}^{(1)}}{r}=0, \end{aligned}$$

(104)

we obtain

$$\begin{aligned} \omega (r)=\frac{LD}{E_{1}}(\zeta ^{-2q}-\zeta ^{-s}), \end{aligned}$$

(105)

with s and L defined in Eq. (49)-2 and Eq. (49)-3. Finally, the strain components of the coating read

$$\begin{aligned} \varepsilon _{r}^{(1)}= & {} \frac{1}{E_{1}}\left[ D\left( 2\nu _{1}(1-q)+L\beta _{1}^{\prime }-1\right) \zeta ^{-2q}\right. \nonumber \\&\left. \quad -LD\beta _{1}^{\prime }\zeta ^{-s}+\left( 1-2\nu _{1}\right) C\cot \phi \right] , \end{aligned}$$

(106)

$$\begin{aligned} \varepsilon _{\theta }^{(1)}= & {} \varepsilon _{\varphi }^{(1)}=\frac{1}{E_{1}} \left[ D\left( q-1+2\nu _{1}-\nu _{1}q-\frac{1}{2}L\beta _{2}^{\prime }\right) \zeta ^{-2q}\right. \nonumber \\&\left. \quad -\frac{LD\beta _{2}^{\prime }}{2}\zeta ^{-s}+\left( 1-2\nu _{1}\right) C\cot \phi \right] . \end{aligned}$$

(107)

The radial displacement component can be determined as follows:

$$\begin{aligned} u_{r}^{(1)}=\varepsilon _{\theta }^{(1)}r= & {} \frac{r}{E_{1}}\left[ D\left( q-1+2\nu _{1}-\nu _{1}q-\frac{1}{2}L\beta _{2}^{\prime }\right) \zeta ^{-2q}\right. \nonumber \\&\left. -\frac{LD\beta _{2}^{\prime }}{2}\zeta ^{-s}+\left( 1-2\nu _{1}\right) C\cot \phi \right] . \end{aligned}$$

(108)

The above unknowns $a_{1},$ $a_{2},$ $b_{1}$  and D, calculated by using the interface continuity conditions, are specified by

$$\begin{aligned} a_{1}= & {} \frac{D(2q-3)}{9\kappa _{1}}+\frac{C\cot \phi }{3\kappa _{1}}, \end{aligned}$$

(109)

$$\begin{aligned} a_{2}= & {} \frac{-D\xi ^{2q}+C\cot \phi }{3\kappa _{2}}, \end{aligned}$$

(110)

$$\begin{aligned} b_{1}= & {} \frac{Dq\rho ^{3}}{6\mu _{1}}, \end{aligned}$$

(111)

and Eq. (51).

By the boundary condition at $r=b,$ the relationship between the pressure $p_{0},$ the isotropic strain volume average $\varepsilon _{0}$ in terms of $\xi =\rho /a$ is derived as in Eqs. (46) and (58). From Eqs. (45), (46), (47), and (59) the expressions of $\kappa _\mathrm{s}^{*}$ and $\kappa _\mathrm{t}^{*}$ can be obtained as in Eqs. (60) and (61).

Finally, when the annular plastic zone extends to the outer surface or, in other words, when the matrix gets totally plastified, the pressure applied on $r=b$ is equal to $p^{\prime \prime }$. The scalar function $\omega (r)$ takes the following form

$$\begin{aligned} \omega (r)=\frac{LD}{E_{1}}\varsigma ^{-2q}+A\varsigma ^{-s}, \end{aligned}$$

(112)

where $\varsigma =r/b$ and D,  A are unknown constants to be specified below. Following the similar calculation procedure from Eq. (105) to Eq. (108), together with the interface continuity conditions at $r=a$ as well as the boundary condition of Eq. (42), the expressions of D,  A and elastic parameter $a_{2}$ can be obtained as follows:

$$\begin{aligned} D= & {} p_{0}+C\cot \phi ,\end{aligned}$$

(113)

$$\begin{aligned} a_{2}= & {} -\frac{1}{3\kappa _{2}}\left[ c^{-2q/3}p_{0}+\left( c^{-2q/3}-1\right) C\cot \phi \right] , \end{aligned}$$

(114)

$$\begin{aligned} A= & {} -\frac{1}{3\beta _{2}^{\prime }\kappa _{2}E_{1}}\left\{ c^{(s-2q)/3}\left( C\cot \phi +p_{0}\right) \left[ \kappa _{2}/\kappa _{1}\left( 3\kappa _{1}-E_{1}\right) \right. \right. \nonumber \\&\left. (q-2)+6\kappa _{2}(1-q)+3\beta _{2}^{\prime }\kappa _{2}L-2E_{1}\right] +c^{s/3}C\cot \phi \nonumber \\&\left. \left[ 2\kappa _{2}/\kappa _{1}\left( 3\kappa _{1}-E_{1}\right) -6\kappa _{2}+2E_{1}\right] \right\} . \end{aligned}$$

(115)

The isotropic strain and strain-rate averages over the coated sphere are given in Eqs. (62) and (63).