Abstract
This paper describes the application of a microscopic defocusing image system to track 3D particle motions in microflow around a microcubic array near a microchannel wall surface. The measurement principle and calibration method were evaluated to provide accurate 3D microparticle location. Particle trajectories were measured in two microchannels. Measured velocity profiles of Hele–Shaw flows for two Reynolds numbers agreed well with theoretical profiles. Three-dimensional particle tracking in fluid flow around a microcubic array exhibited quasi-periodic and non-periodic trajectory modes. The experimental results indicated that 3D particle motions are spatially and time dependent even when the flow rate is constant, and microparticle trajectories may deviate from steady flow streamlines.
Similar content being viewed by others
1 Introduction
Great progress in fluid diagnosing methods at micro- and nanoscales has been made in recent decades promoting developments in physics, chemistry, biology, medicine, and microelectromechanical systems (MEMS). Most previous studies have focused upon flow structure measurements in microdevices (Cierpka and Kähler 2012). Transportation, separation, and collection of solid particles, biological cells, liquid droplets, and gas bubbles have become very important in the study of microfluidic internal flows (Stone et al. 2004).
The influence of complex three-dimensional (3D) wall surface structures on internal flows at micro- or nanoscales should also be considered, and many studies have investigated the influence of wall roughness on flow field and friction characteristics (Natrajan and Christensen 2010; Gamrat et al. 2008; Wang and Wang 2007). Recent studies have indicated that hierarchical micro- or nanostructures on a solid surface can have significant effects on hydrophobic and hydrophilic characteristics, changing flow structure and friction characteristics significantly (Nosonovsk and Bhushan 2008; Ou and Rothstein 2005; Choi and Kim 2006; Lu et al. 2010). However, there are few experimental studies of wall surface roughness flow field influence (Gamrat et al. 2008); particularly, the motion of microparticles influenced by 3D wall surface microstructure has been seldom reported.
Various optical measurement techniques related to particle motions on the microscopic scale have been recently developed. Microscopic particle image velocimetry (micro-PIV) and microscopic particle tracking velocimetry (micro-PTV) have allowed detailed detection of full field microparticle motion. The micro-PIV technique, first introduced by Santiago et al. (1998), captures two or more images of moving particles and analyzes their motion using spatial correlation to infer the fluid velocity field (Wereley and Meinhart 2010). On the other hand, micro-PTV is based on single-particle position recognition to detect individual particle trajectories. Particle motion behaviors and local flow characteristics can be investigated by tracking 3D particle trajectories. To investigate the microparticle motions influenced by wall surface microstructure, 3D microparticle tracking techniques need to be employed. Up till now, several 3D microparticle tracking techniques have been developed following different principles.
Stereoscopic micro-PTV techniques measure all three velocity components of particles using two cameras. Out-of-plane particle velocity is derived from two different perspectives, i.e., at least two different views are required. Both cameras record the illuminated particles, and in-plane velocity vectors can be estimated using PTV algorithms (Bown et al. 2006). However, micro-PIV technique microscope objectives have a large numerical aperture, which limits off-axis viewing angle (Wereley and Meinhart 2010). In addition, the technique requires complex calibration (Cierpka and Kähler 2012).
Digital holographic micro-PTV applies digital holography to the microscopic domain. Particle spatial positions can be reconstructed from holographic images using the image sensor to record scattered and non-scattered light interference patterns as a hologram. Digital holography for microflows was first introduced by Yang and Chuang (2005), and Satake et al. (2006) subsequently developed a holographic particle tracking method. However, the technique requires significant computational overhead for reconstruction. In-line holography requires coherent light from opposite the camera; hence, a second optical access is necessary and particle concentration is limited (Cierpka and Kähler 2012).
Astigmatism micro-PTV breaks the axial symmetry of an optical system, allowing particle depth coding in 2D images. A cylindrical lens replaces the optical field lens, creating a deformation imaging system (Hain et al. 2009; Cierpka et al. 2011). The main advantage of this method is relatively low cost and easy application that enables full 3D and three-component (3D3C) measurement with standard microscope equipment. The influence of unwanted image aberrations can be excluded by calibration (Cierpka and Kähler 2012).
Defocusing particle image techniques use different particle image patterns to obtain the particle depth using diffraction, or fix a mask with pinholes in the optical system (Park and Kihm 2006; Yoon and Kim 2006; Pereira et al. 2007; Peterson et al. 2008). 3D particle tracking can be relatively easily realized using defocusing particle image techniques, which have been widely applied to measure particle trajectories in 3D flow structures.
Park and Kihm (2006) developed microdefocusing from its macroscopic counterpart (Willert and Gharib 1992) to track the velocity of 500-nm-diameter fluorescent particles in a 100 × 100 μm microchannel. This method tracks line-of-sight flow vectors by correlating diffraction pattern ring size variations with defocusing distances of small particle locations. Yoon and Kim (2006) used a high-speed camera (1000 fps) and a pinhole mask to track particle trajectories in 768 × 388 × 50 μm microchannels. Depth calibration was performed in a microvolume, and compensation functions were obtained. Effects of pinhole masks with different pattern sizes were also described. Pereira et al. (2007) applied this technique to measure 2-μm-diameter fluorescent particles in evaporating liquid. A microvolume 400 × 300 μm2 and 150 μm depth was mapped using an inverted microscope equipped with a 20× objective lens. Peterson et al. (2008) measured the velocity profile in a 50-μm-deep channel by manually identifying the particles and calculating the size of the outer diffraction ring. They found particles with 3 μm diameter were sufficient for later data processing. However, large uncertainty can be generated due to the short illumination time of the small particles (100 ms) and the consequential low signal-to-noise ratio (SNR) (Cierpka and Kähler 2012). Lu et al. (2008) applied the same technique to measure zebra fish embryonic heartbeat patterns. Fluorescent tracer particles (1 μm) were injected into the blood stream, and velocity fields of cardiovascular blood flow and trajectories of heart-wall motions were obtained. Lin et al. (2008) proposed an annular-aperture-based defocusing technique for 3D particle metrology from a single camera view. They showed that depth uncertainty of 23 μm could be achieved over a range of 10 mm for macroscopic systems. Nasarek (2010) measured toroidal flow in a microchannel with a depth of 50 μm. Measurement accuracy was estimated to be ± 2 pixels, which was ± 2 μm for the optical setup employed. Deviation in the z direction was determined from the mean standard deviation of the measured radii from the calibration procedure. Tien et al. (2014) developed color-coded 3D microparticle tracking velocimetry based on Tien et al. (2008) and applied it to microbackward-facing step flows. Experimental location uncertainties were less than 0.10 and 0.08 μm for in-plane and 0.82 μm for out-of-plane components, respectively. Displacement uncertainties were 0.62 and 0.63 μm for in-plane and 0.77 μm for out-of-plane components, respectively. Winer et al. (2014) developed a defocusing image technique to determine 3D locations of cell-sized particles in microscale flows, which was the first implementation of this technique for particle focusing applications.
In this study, defocusing particle image technique was employed to investigate 3D microparticle motions in the microchannels. The current paper describes the construction of a high-speed defocusing particle image system and related calibration based on Yoon and Kim (2006), and particle trajectories in two different microchannels were measured. The primary contribution of this study is to obtain 3D trajectories of particles in the flow around a microcubic array near the wall surface, identifying two distinct trajectory modes.
2 Experimental system and methods
2.1 Defocusing image technique
Figure 1 shows the defocusing image optical principle. Fluorescence passes through the 3-pinhole mask and forms an image on the CMOS sensor. The image of an out-of-plane particle will be split into three image points composing a regular triangle due to the mask, where the length and direction of the regular triangle are determined by the particle depth. The particle location in the image plane is the triangle center, which is also the circumcircle center. The three image points coincide at a single image point when the particle is located in the focal plane. The out-of-plane particle depth is correlated with the optical geometry and triangle scale of the three image points. Hence, we can develop a calibration function between the particle depth and image characteristics based on the device geometry. “Appendix” shows the detailed defocusing image processing used in this study.
2.2 Experimental system
Figure 2 shows a schematic of the high-speed microparticle tracking system based on the defocusing image technique developed by Yoon and Kim (2006). The system was constructed by adapting an existing inverse micro-PIV system (LaVision, Germany). The light source was a 532 nm, 5W continuous laser (Beijing ZK Laser Co., Ltd., China). Particle images were captured using a MEMRECAM HX-6 type CMOS high-speed camera (NAC, Japan), with maximum 5000 fps capacity, and sensor pixel pitch = 11 μm. The camera was set to capture 640 × 640 pixel images at 1000 fps. To obtain high-quality particle images, a 20×/0.4 (M/NA) L D Plan-Neofluar microscope objective (Carl Zeiss, Germany) was employed to observe particle motions within the 205 × 205 × 50 μm view field. Fluorescent particles with 2 μm diameter (Thermo scientific, USA) were chosen for the particle tracking experiments. Particle material was polystyrene (PS), with 1.05 g/cm3 density, and excitation and emission peaks at 542 and 612 nm, respectively. A high-precision 3D translation stage was installed in an existing inverse micro-PIV system to accurately control the 3D position of the microchannels. The minimum controllable displacement of 3D coordinates was 100 nm. Flows were driven by a syringe pump (Longer LSP02-1B type, China) at set flow rates.
2.3 Experimental materials and methods
2.3.1 Hele–Shaw flows
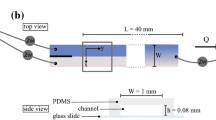
Two particle trajectory experiments were implemented with Hele–Shaw flows to verify the implemented defocusing image method and system. We fabricated a 5 mm × 2 mm × 50 μm (length × width × depth) microchannel from polydimethylsiloxane (PDMS) and covered it with a glass plate, as shown in Fig. 3, where Fig. 3a shows the streamwise direction and Fig. 3b shows the cross section. The microchannel had 40:1 aspect ratio (width/depth), so flow fields between the top and the bottom wall surfaces can be considered as typical 2D Poiseuille flows, i.e., side wall effects can be ignored.
Deionized water was driven into the microchannel from the inlet by the syringe pump. The outlet was connected to the atmosphere through a thin short plastic pipe. Aqueous suspensions of fluorescent particles (solid volume concentration = 1%) were mixed with deionized water to produce a particle density ratio of 1:1000. Particle images were acquired through the inverted microscope objective at 1000 fps. Particles moved with the water flow in different planes, noted as different colors in Fig. 4, and particle trajectories were obtained using the high-speed defocusing image system.
Drawing the particle trajectories was time-consuming because particle density was low. Since the velocity profiles in the z direction may be expected to be symmetrical parabolic curves (Poiseuille flows), measurements were mainly implemented within the top half of the microchannel region to decrease data processing. Up to 25,000 particle images were acquired, and individual particles at different depths of the microchannel (Fig. 4) were tracked to obtain their 2D trajectories and experimental velocity profiles, which were compared with the theoretical 2D streamlines and velocity profiles for flows between parallel plates.
2.3.2 Flow around microcubic arrays
Figure 5 shows the fabricated microchannel structure, comprising a set of microcubes in a cubic arrangement, with 131 and 25 microcubes in the streamwise and spanwise directions, respectively. Table 1 shows the microchannel and microcubic array geometrical parameters. Particle motion and trajectories near the complex wall surface were obtained using the proposed 3D micro-PTV defocusing image system. Syringe pump flow rate was set as q = 371.6 µl/h; hence, Re = 0.05 (Re = hU/ν, where U = q/A is the average velocity over the microchannel cross section, A = Wh is the cross-sectional area, and ν = 1 × 10−6 m2/s), and the flow around the microcubic array is typical Stokes flow (Re ≪ 1). The particle tracking measurement area was located near the center of the microchannel array, with four microcubes in the field of view. Defocused particle images were acquired at the same frame rate as discussed previously (1000 fps), and the 3D particle trajectories were obtained.
For the particle tracking experiments, we employed Wiener filtering to remove image noise, and Video Spot Tracker (VST, v07.02) software to track the defocused particle image centroid. VST tracked the three points of defocused particle images on the horizontal plane (xy-plane) and recorded their coordinates simultaneously. Particle trajectories were subsequently synthetized using Eqs. (A.1)–(A.3). Particle depth was derived from the depth calibration function, Eqs. (A.4) and (A.5). Accurate horizontal coordinates were obtained by correcting the centroid using Eqs. (A.6) and (A.7).
3 Experimental results and discussion
3.1 Particle trajectories in Hele–Shaw flow
Figure 6 shows particle trajectories for Re = 0.025 and 0.05 (Re = Ud/ν, where U is the average velocity over the microchannel cross section, d = 50 μm is the microchannel depth, and ν = 1 × 10−6 m2/s is the kinematic viscosity of water). Colored circles denote tracked particles, with different colors representing different depths in the microchannel. Particle trajectories for both Hele–Shaw flows form a group of parallel straight lines along the depth direction from the top wall of the microchannel. The interval between adjacent particles represents the distance particles move at the (constant) capture rate. For both flow rates, the interval increases with increasing distance from the wall. Thus, fluid velocities increase with increasing distance from the wall. These outcomes are consistent with typical shear flow field characteristics. Figure 6a shows that the distance between subsequent measurement points becomes progressively smaller going from left to right in the topmost particle trajectory, which may be because the stronger fluid viscous effect near wall surface slows the particles.
To validate the experimental particle trajectories, particle Stokes numbers, St, at low Reynolds number, are calculated as (Zhang et al. 2016)
where ρ p and ρ f are particle and fluid density, respectively, d p is the particle diameter, U is the average fluid velocity, and μ is the dynamic viscosity. In this study, ρ p ≈ ρ f , hence
Equation (2) indicates that St is proportional to Re (for fixed d p /d), so St ≪ 1 (Re ≪ 1). The Stokes number is the ratio of particle response time to flow response time. A particle with high St will require longer time to adjust to the flow, whereas one with low St will adjust faster (Zhang et al. 2016). Since St ≪ 1, particle flow response will be very quick, i.e., particle trajectories should agree well with streamlines.
Figure 7 compares experimental and theoretical velocity profiles for Re = 0.025 and 0.05. The experimental velocity in a particle trajectory (Fig. 6) was determined based on the averaged particle displacements in this particle trajectory and the time interval. Theoretical velocity profiles were determined for Poiseuille flow between two parallel planes,
where U = 0.5 and 1 mm/s for Re = 0.025 and 0.05, respectively; z0 = − 61.6 ± 2 μm is the depth coordinate to the bottom wall surface, based on depth field = 4 μm for the 20× microscope objective. The theoretical velocity profiles agree well with experimental points. Since the velocity profile is a function of z2 and depth calibration error is significantly larger than for the x and y directions (Fig. 17), measurement errors mainly arise from depth calibration errors, with lesser contribution from image quality and particle recognition.
3.2 Particle trajectories around a microcubic array fabricated on the wall
3.2.1 Particle tracking
Figure 8 shows overlapping particle trajectories for two depth regions, approximately − 17 to − 26 µm and − 25 to − 45 µm (Fig. 8a, b, respectively; where z = 0 is 10 μm below the bottom surface in Fig. 5a). The former is far from the microcubes, and the latter is in or close to the microcubes. Trajectory depth is denoted by color, as shown in the color bars. Particle trajectories tend to follow a wave pattern throughout the flow field.
Particle tracking through the microchannel structure around a microcubic array fabricated on the wall for: a z ≥ − 26 μm, b z ≤ − 25 μm, c top view of numerically computed Stokes flow streamlines around the microcubic array (Hu et al. 2003)
Figure 8c compares particle trajectories with numerically computed streamlines for 3D Stokes flow around the microcubic array (Hu et al. 2003), where the fluid converges in the wider space between two elements and diverges in the narrower path, periodically. (The top and bottom streamlines in this plot seem to intersect with the cube geometry, which may be due to drawing error.) Experimental particle tracking and numerical simulation for 3D Stokes flow both exhibit the periodic wave pattern and amplitude variations. From Eqs. (1) and (2), St ≪ 1, so particle trajectories should agree well with the streamlines. Thus, we can conclude that the observed particle trajectories were consistent with that of steady Stokes flow streamlines overall.
In contrast to the numerical solution for steady Stokes flow, particle motion will be disturbed by various small perturbations, causing the particles to deviate from the steady Stokes flow streamlines. The 3D microchannel structure will increase the probability of disturbance. Two trajectory modes were observed in the experiments, as shown in Fig. 9 for the − 25 to − 45 μm depth region. The flow conditions between Figs. 8 and 9 are the same. Quasi-periodic trajectory mode particle trajectories agreed well with steady Stokes streamlines, as shown in Fig. 8c, whereas non-periodic trajectory mode particle trajectories showed significant departures from steady Stokes flow streamlines. The flow was not absolutely steady experimentally, so we use “quasi-periodic” instead of “periodic” in this study. Figure 9a (taken from Fig. 8b) shows that particle trajectories exhibited a quasi-periodic wave pattern in the horizontal plane. Different situations occur for some local positions (Fig. 9b), with non-periodic trajectories in the same positions, e.g., particle trajectories A, B, and C deviate significantly from the steady streamline. Deeper particles, e.g., trajectory A, tend to show larger deviation, where the trajectory turns from the right side of the upstream microcube to the left side of the downstream microcube (right and left defined facing the streamwise direction), breaking particle trajectory periodicity. Thus, particle motion does not absolutely follow the streamlines under constant flow rate.
Particle deviation from theoretical trajectories or streamlines can be attributed to several factors. Flow inertia is an important reason for particle migration across streamlines in macroscopic pipes (Segré and Silberberg 1962; Matas et al. 2004). Di Carlo et al. (2009) and Abbas et al. (2014) showed that inertial cross-streamline migration occurred at microscales. Individual spherical particles cannot exhibit cross-streamline migration under viscosity-dominated Stokes flow (Bretherton 1962; Di Carlo et al. 2009; Abbas et al. 2014). Diameters of flow-tracing particles for micro-PIV/PTV typically range from 200 nm to 2 μm, and Brownian motion may cause random thermal noise in the velocity fields (Wereley and Meinhart 2010). Thus, the flow-tracing particles can be perturbed from the stochastic fluctuations in Stokes flows, deviating from their original trajectories, particularly for strongly disturbed flow regions. Sufficiently large particles, e.g., 2 μm diameter, can effectively dampen the influence of fluid stochastic fluctuations, reducing the probability of particle deviation from streamlines. Hence, the experimental observations indicate that non-periodic trajectory modes maybe result from stochastic fluctuations in strongly disturbed flow fields, but are not the dominant mode since the flow-tracing particles were sufficiently large. Further study will implemented to determine the exact cause for streamline crossing in this particular type of flow.
3.2.2 Three-dimensional quasi-steady trajectory structure
Figure 10 shows a group of typical particle trajectories around two adjacent microcubes along the streamwise direction, taken from Fig. 8, viewed from several directions. Figure 10a, b shows the particle trajectories on the horizontal (xy) and vertical (xz) planes, respectively, within the − 17 to − 26 µm depth region. Figure 10c, d shows particle trajectories on the horizontal and vertical planes within the − 25 to − 45 µm depth region, respectively.
Figure 10e shows the 3D trajectory structure, where the vertical planes were created by mirroring actual measurements. Comparing Fig. 10a, c, two trajectory modes are apparent. The quasi-periodic mode is the main trajectory mode in the region far from microcubes (− 17 to − 26 µm), whereas a non-periodic mode occurs in the deeper region (− 25 to − 45 µm) most likely due to strong disturbance from the microcubes. Comparing Fig. 10b, d, particle trajectories projections on the vertical plane show waveforms due to the microcube periodic peak and valley structure, with increased amplitude closer to the microcubes. Figure 10e shows that particle trajectories alternately converge and diverge to form 3D spatial curves embracing the microcubes, presenting a complete picture of 3D particle migrations in Stokes flow around a microcubic array on the wall surface.
4 Conclusions
In this study, a high-speed microscope defocusing particle image system based on Yoon and Kim (2006) was constructed to track microparticle motions in the flow field, and a calibration function was applied between the configuration parameters for defocusing the particle image and the particle’s out-of-plane position.
To verify the reliability of the proposed defocusing particle image tracking system and define measurement accuracy, flows between parallel plates were measured for Re = 0.025 and 0.05. The results show that particle trajectories for both flows form a group of parallel straight lines along the depth direction from the top wall of the microchannel. The measured velocity profiles showed good agreement with theoretical velocity profiles of 2D Poiseuille flows between two parallel plates.
Particle trajectories were measured for 3D flow around a microcubic array fabricated on the wall surface. The experimental results showed that particle trajectories were consistent with 3D Stokes flow streamlines. Quasi-periodic and non-periodic particle trajectory modes were observed. The former was the main trajectory mode, with the latter occurring in or close to the microcubic array, most likely due to stronger disturbance from the 3D structure.
References
Abbas M, Magaud P, Gao Y et al (2014) Migration of finite sized particles in a laminar square channel flow from low to high Reynolds numbers. Phys Fluids 26:123301
Bown MR, MacInnes JM, Allen RWK et al (2006) Three-dimensional, three-component velocity measurements using stereoscopic micro-PIV and PTV. Meas Sci Technol 17:2175–2185
Bretherton FP (1962) The motion of rigid particles in a shear flow at low Reynolds number. J Fluid Mech 14:284–304
Choi CH, Kim CJ (2006) Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys Rev Lett 96:066001
Cierpka C, Kähler CJ (2012) Particle imaging techniques for volumetric three-component (3D3C) velocity measurements in microfluidics. J Vis 15:1–31
Cierpka C, Rossi M, Segura R et al (2011) On the calibration of astigmatism particle tracking velocimetry for microflows. Meas Sci Technol 22:015401
Di Carlo D, Edd JF, Humphry KJ et al (2009) Particle segregation and dynamics in confined flows. Phys Rev Lett 102:094503
Gamrat G, Favre-Marinet M, Le Person S et al (2008) An experimental study and modelling of roughness effects on laminar flow in microchannels. J Fluid Mech 594:399–423
Hain R, Kähler CJ, Radespiel R (2009) Principles of a volumetric velocity measurement technique based on optical aberrations. In: Nitsche W, Dobriloff C (eds) Imaging measurement methods for flow analysis, Notes on numerical fluid mechanics and multidisciplinary design, vol 106. Springer, Berlin, pp 1–10
Hu YD, Werner C, Li DQ (2003) Influence of three dimensional roughness on pressure-driven flow through microchannels. J Fluids Eng 125:871–879
Lin D, Angarita-Jaimes NC, Chen S et al (2008) Three-dimensional particle imaging by defocusing method with an annular aperture. Opt Lett 33:905–907
Lu J, Pereira F, Fraser SE et al (2008) Three-dimensional real-time imaging of cardiac cell motions in living embryos. J Biomed Opt 13:014006
Lu S, Yao ZH, Hao PF et al (2010) Drag reduction in ultrahydrophobic channels with micro-nano structured surfaces. Sci China 53:1298–1305
Matas JP, Morris JF, Guazzelli É (2004) Inertial migration of rigid spherical particles in Poiseuille flow. J Fluid Mech 515:171–195
Nasarek R (2010) Temperature field measurements with high spatial and temporal resolution using liquid crystal thermography and laser induced fluorescence. PhD dissertation, Technische Universität Darmstadt, Germany
Natrajan VK, Christensen KT (2010) The impact of surface roughness on flow through a rectangular microchannel from the laminar to turbulent regimes. Microfluid Nanofluid 9:95–121
Nosonovsk M, Bhushan B (2008) Mutltiscale dissipative mechanisms and hierarchical surfaces: friction, superhydrophobicity and biomimetics. Springer, Berlin
Ou J, Rothstein JP (2005) Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces. Phys Fluids 17:103606
Park JS, Kihm KD (2006) Three-dimensional micro-PTV using deconvolution microscopy. Exp Fluids 40:491–499
Pereira F, Lu J, Castaño-Graff E et al (2007) Microscale 3D flow mapping with µDDPIV. Exp Fluids 42:589–599
Peterson SD, Chuang H, Wereley ST (2008) Three-dimensional particle tracking using microparticle image velocimetry hardware. Meas Sci Technol 19:115406.1–115406.8
Santiago JG, Werely ST, Meinhart CD et al (1998) A particle image velocimetry system for microfluidics. Exp Fluids 25:316–319
Satake S, Kunugi T, Sato K et al (2006) Measurements of 3D flow in a micro-pipe via micro digital holographic particle tracking velocimetry. Meas Sci Technol 17:1647–1651
Segré G, Silberberg A (1962) Behaviour of macroscopic rigid spheres in Poiseuille flow Part 2. Experimental results and interpretation. J Fluid Mech 14:136–157
Stone HA, Stroock AD, Ajdari A (2004) Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu Rev Fluid Mech 36:381–411
Tien WH, Kartes P, Yamasaki T et al (2008) A color-coded backlighted defocusing digital particle image velocimetry system. Exp Fluids 44:1015–1026
Tien WH, Dabiri D, Hove JR (2014) Color-coded three-dimensional micro particle tracking velocimetry and application to micro backward-facing step flows. Exp Fluids 55:1684–1697
Wang HL, Wang Y (2007) Influence of three-dimensional wall roughness on the laminar flow in microtube. Int J Heat Fluid Flow 28:220–228
Wereley ST, Meinhart CD (2010) Recent advances in micro-particle image velocimetry. Annu Rev Fluid Mech 42:557–576
Willert CE, Gharib M (1992) Three-dimensional particle imaging with a single camera. Exp Fluids 12:353–358
Winer MH, Ahmadi A, Cheung KC (2014) Application of a three-dimensional (3D) particle tracking method to microfluidic particle focusing. Lab Chip 14:1443–1451
Yang CT, Chuang HS (2005) Measurement of a microchamber flow by using a hybrid multiplexing holographic velocimetry. Exp Fluids 39:385–396
Yoon SY, Kim KC (2006) 3D particle and 3D velocity field measurement in a microvolume via the defocusing concept. Meas Sci Technol 17:2897–2905
Yoon SY, Kihm KD, Kim KC (2011) Correlation of fluid refractive index with calibration coefficient for micro-defocusing digital particle image velocimetry. Meas Sci Technol 22:037001
Zhang L, Jebakumar AS, Abraham J (2016) Lattice Boltzmann method simulations of Stokes number effects on particle motion in a channel flow. Phys Fluids 28:063306
Zhao PJ (2015) Study on the three-dimensional particle tracking velocimetry based on the defocusing microscopic image, Master dissertation, China Jiliang University, China
Acknowledgements
This study was funded by the National Natural Science Foundation of China (Grants 11472261 and 11172287) and the High Level Scholarship Foundation of Jinling Institute of Technology. Their support is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Three-pinhole mask
A three-pinhole mask was installed behind the microscope objective to acquire the defocused particle images, as shown in Fig. 11. Following Yoon and Kim (2006), holes were chosen to be d = 2 mm and arranged in a regular triangle where the circle incorporating the pinhole centers had a diameter, D = 4 mm.
Particle coordinates in the image plane can be expressed as
and
where D is the circumcircle diameter of the regular triangle; a, b, and c are the distances between the three points; p = (a + b+c)/2; (X, Y) is the particle coordinate in the image plane; and (X1, Y1), (X2, Y2), and (X3, Y3) are the coordinates of the three defocused points, respectively, in the image plane.
1.2 Defocused particle image and recognition
Figure 12 shows a typical set of defocused particle images for various planes away from the reference plane, analogous to Yoon and Kim (2006). The regular triangles composed by the defocused images show inverse configurations for particles located at symmetrical positions with respect to the focal plane.
This study adopted similarity degree (Yoon and Kim 2006) to recognize defocused particle images, as shown in Fig. 13 for 29 images at one depth.
1.3 Calibration
To calibrate the system, particles were fixed on a glass plate by evaporating a low particle density solution, and defocused images were acquired at every 2 μm distance between the glass plate and microscopic objective using the high-precision 3D translation stage along the out-of-plane direction. The working fluid for the particle tracking experiments was deionized water, whereas for calibration the particles were exposed in air. Therefore, the calibration particle depth will deviate from the real particle depth due to the different refractive indexes between water and air. Yoon et al. (2011) suggested a correction coefficient
where (∂z/∂D)fluid and (∂z/∂D)ref are the calibration coefficients, and nfluid and nref are the refractive indexes for the working and reference (used in the calibration) fluids, respectively.
Once (∂z/∂D)ref is determined experimentally using a reference fluid with nref, the calibration coefficient for a working fluid with nfluid can be determined from Eq. (A.4) (Yoon et al. 2011). As the working (deionized water) and reference (air) fluid refractive indexes are 1.333 and 1.0003, respectively, calibration error after correction calculated from Eq. (A.4) is smaller than 1.38%. To further reduce calibration error, we averaged 5800 samples from 200 defocused images of 29 sample particles, with depth z = − 70 to − 14 µm at 2-µm intervals, as shown in Fig. 14. The defocused image circumcircle diameter showed a good linear relationship with depth,
where a = (∂z/∂D)ref is the calibration coefficient, b is constant, and nfluid/nref = 1.332. Least squares fitting showed a = − 0.887 and b = 2.29, with correlation coefficient R2 = 0.9997.
1.4 Compensation method for particle position drift
Particle position drifts occur when calculating the depth coordinate of calibration particles, which leads to position uncertainties in all three directions. To solve this, drifts along x and y coordinates were tested for each plate location, as shown in Fig. 15. Consistent drift is evident across the depth range in the x direction (Fig. 15a), with approximately 6 pixels maximum drift, whereas y direction drift is somewhat less consistent (Fig. 15b) and also somewhat larger, with maximum drift > 10 pixels.
Therefore, we employed bivariate polynomial compensation (Yoon and Kim 2006) to correct for coordinate drift,
and
where x, y, and z are the physical particle coordinates; a0–a5 and b0–b5 are compensation coefficients in the x and y directions, respectively, as listed in Table 2. In the compensation procedure, x and y coordinates of the measurement points in Fig. 16 are substituted into Eqs. (A.6) and (A.7), establishing two groups of overdetermined equations (the number of equations is more than unknown quantity) about coefficients a0–a5 and b0–b5. The least squares method was employed to solve the two groups of equations.
Figure 16 shows the resultant corrected position coordinates using 30 pictures of particle images (29 particle images in every picture) and a total of 870 groups of particle image data. Although some drift remains after compensation, it is significantly and sufficiently decreased.
To evaluate measurement accuracy, root-mean-square errors (RMSE) for x, y, and z directions are calculated as
and
where n is the total number of particle images; subscripts com, cal, and meas refer to coordinates for compensation, calibration particles in the reference plane (z = 0), and measurement points, respectively.
Figure 17 shows that Rx, Ry, and Rz fluctuate around averages of 0.1468, 0.1859, and 0.4329 µm, respectively, with little evidence of remaining depth-related drift. Considering the various factors, including the slight nonlinear variation of image diameter with calibration depth (Pereira et al. 2007; Zhao 2015), depth direction RMSE is 2–3 times that of the horizontal directions, which is consistent with Yoon and Kim (2006) and Pereira et al. (2007).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, H., Zhao, P. Tracking microparticle motions in three-dimensional flow around a microcubic array fabricated on the wall surface. Microfluid Nanofluid 22, 30 (2018). https://doi.org/10.1007/s10404-018-2047-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10404-018-2047-3