Abstract
Although Scots pine (Pinus sylvestris L.) is one of the most economically important European timber trees, there is still insufficient data about biomass variability and its relationships with stand features. Therefore, we aimed: (1) to develop biomass models for different aboveground biomass components at tree and stand levels, as well as biomass conversion and expansion factors (BCEFs), (2) to assess the relationships between stand parameters and aboveground biomass and BCEFs and (3) to compare stand biomass obtained using BCEFs with models developed based on stand parameters (age, basal area, stand volume and mean height). Using a chronosequence (3–117 years old) of 120 plots within even-aged pure Scots pine stands and 791 sample trees, we prepared tree- and stand-level allometric equations and BCEFs for aboveground biomass determination. Using stand age, density, stand volume and mean height, we prepared a set of models for biomass and BCEFs. Our study indicated that stand biomass increased with increasing height, volume and age and with decreasing stand density during stand development. Stand-level models provided better accuracy than BCEF-based models. The best predictors of biomass were stand volume and mean height. We also confirmed highly dynamic increases in stand biomass and decreases in BCEFs in the youngest phase of stand growth and relative stabilization in later stages of Scots pine stand development. The models obtained may be used in large-scale forest biomass inventories and increase our knowledge of carbon sequestration in forest biomass.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Stand biomass is one of the most important measures of space and resource utilization in forest ecosystems. As carbon content in plant tissues is relatively constant, in comparison with the variability of stand biomass (e.g., Lehtonen et al. 2004; Martin and Thomas 2011; Jagodziński et al. 2012), assessment of biomass allows calculation of how much carbon has been sequestrated in an ecosystem. This utility of biomass calculation confers its high importance in carbon inventories, allowing estimation of carbon sequestration in forests. In the age of changing climate (Thuiller et al. 2011; Sohngen and Tian 2016) and increasing concentration of CO2 in the atmosphere (IPCC 2013), increasing accuracy of biomass estimation is an urgent need of science. This is especially important, as forests are one of the most important terrestrial pools of carbon (Pan et al. 2011) and may help to mitigate negative effects of climatic change (Chmura et al. 2010; Lindner et al. 2014; Dyderski et al. 2018).
Usually stand biomass may be assessed using the two main approaches: allometric equations at both tree and stand levels (e.g., Baskerville 1972; Zianis et al. 2005; Zasada et al. 2008; Xie et al. 2016; Forrester et al. 2017) and stand-level assessments based on biomass conversion and expansion factors (e.g., Lehtonen et al. 2004; Teobaldelli et al. 2009; Wojtan et al. 2011; Jagodziński et al. 2017). The former is a regression model between two variables expressed in units of different dimensions. The most common are tree-level models, allowing for biomass estimation based on dimensions of single trees. This tool uses general allometric rules of biomass scaling according to the organism’s dimensions (Weiner 2004; McCarthy and Enquist 2007; Poorter et al. 2015). Although these models usually have high accuracy (Zianis et al. 2005), their applicability is limited only to datasets containing single tree observations. For that reason usage of tree-level methods of biomass estimation is time and money demanding. BCEFs are coefficients which allow calculation of stand biomass using information on volume (Eggleston et al. 2006; Somogyi et al. 2007). As BCEFs are volume dependent, their application is only possible when this information is available. However, most forest inventories provide this data, as stand volume is the most important parameter from the economical point of view. For that reason, BCEFs are more useful for cases of large-scale analyses (Neumann et al. 2016). Nevertheless, BCEFs are developed using biomass calculated from tree-level inventories; thus, their accuracy is biased at the level of tree-level biomass estimation and development of stand-level models.
Stand biomass, as a function of resource availability, also depends on the other stand features. Allometric trajectories of biomass models are modified by stand age (Wirth et al. 2004; Lehtonen et al. 2004; Jagodziński et al. 2017). Biomass production and allocation also depend on stand density (Jagodziński and Oleksyn 2009a, b). Also, measures of stand density and dimensions, such as volume and basal area, are often used in modeling of stand biomass or BCEFs (Teobaldelli et al. 2009; Castedo-Dorado et al. 2012; Lehtonen et al. 2016; Jagodziński et al. 2017). Biomass allocation patterns (i.e., ratio of stem, branches, root and foliage masses), influencing stand biomass, also differ among habitat types. For example, site-specific allometric models were provided for peatlands (e.g., Laiho and Finér 1996; Hytönen and Aro 2012; Lehtonen et al. 2016), post-agricultural sites (e.g., Uri et al. 2007; Bijak et al. 2013; Jagodziński et al. 2014) or post-industrial sites (e.g., Pietrzykowski and Socha 2011; Kuznetsova et al. 2011; Jagodziński et al. 2014). The differences in growth of trees are also connected with provenances and genotypes, reflecting adaptations to soil and climate (e.g., Oleksyn et al. 1999; Bussotti et al. 2015; Chakraborty et al. 2016). For that reason, for large-scale inventories there is a need to provide generalized models (e.g., Wirth et al. 2004; Muukkonen 2007; Forrester et al. 2017), taking into account stand parameters which are usually available in forest inventory datasets.
Scots pine (Pinus sylvestris L.) is the most extensively distributed tree species in Eurasia (Houston Durrant et al. 2016). Its range covers an area from Spain to Eastern Siberia, from boreal to Mediterranean zones. This species typically dominates in poor habitats, connected with sandy soils and harsh climates; however, it has a broad ecological amplitude. Scots pine is able to colonize both extremely dry and extremely wet sites (Ellenberg 1988; Houston Durrant et al. 2016). For that reason, this species has high economic importance in Europe, with a 20% share of timber production (Houston Durrant et al. 2016). Nevertheless, our knowledge about its biomass production is disproportionally low relative to its geographical range and economic usage (Cienciala et al. 2006; Forrester et al. 2017). For Scots pine, Zianis et al. (2005) provided 205 allometric equations for the entirety of Europe. Forrester et al. (2017) found 107 allometric models useful for large-scale analyses, rejecting those not based on diameter at breast height. BCEFs and allometric equations for Scots pine biomass estimation were also reviewed by Neumann et al. (2016) and by Lakida et al. (1996). Numerous raw data of tree- and stand-level biomass are provided in Schepaschenko et al. (2017). Although accounting for large extents within Scots pine geographical range, as well as its variability in ecophysiology and patterns of biomass allocation (e.g., Oleksyn et al. 1999; Lehtonen 2005; Finér et al. 2007; Jagodziński and Oleksyn 2009a; Repola and Ahnlund Ulvcrona 2014; Bronisz and Zasada 2016), this number of biomass estimation models might still be insufficient for proper reporting of carbon sequestration in forest ecosystems. This insufficiency results from local specificities and biogeographic trends. Moreover, despite studies on stand biomass of Scots pine in Poland, at this time there are no published studies covering a whole chronosequence of this species biomass in Poland using both tree- and stand-level approaches. Thus, we aimed: (1) to develop biomass models for different aboveground biomass components at tree and stand levels, as well as biomass conversion and expansion factors (BCEFs) for Scots pine, (2) to assess the relationships between stand parameters and aboveground biomass and biomass conversion and expansion factors (BCEFs) and (3) to compare stand biomass obtained using BCEFs with models developed based on stand parameters (age, basal area, stand volume and mean height).
Methods
Study sites and material
We established 120 plots in pure even-aged Scots pine stands ranging from 3 to 117 years old and on all site types typical for this species, including long-term forest (forest growing on forest sites, in contrast to first-generation forests), post-agricultural and post-industrial sites (Table 1, S1). The plots were established during different studies; thus, their selection was usually connected with visual estimation as being representative of larger areas of neighborhood forests. Plot sizes varied from 0.008 to 0.6125 ha, to maintain sufficient numbers of trees to analyze stand features (at least 100 trees per plot). Sample stands grew in a wide range of habitats, mostly poor and mesic soils, which are potential sites of pine forests, and poor sites of oak forests, constituting optimal sites for Scots pine (Ellenberg 1988). Within our dataset, we also included stands established in habitats of fertile deciduous forests, where Scots pine was planted to increase its wood production. All plots were located in lowlands of Western and Central Poland, in a zone of transition between maritime and continental temperate climate (51.21–53. 92°N; 14.34–18.59°E).
Field and laboratory methods
Diameters of all trees and heights of at least 20% of trees were measured within each study plot. Within study plots, we selected and harvested four to twelve sample trees to obtain weight of the biomass components. We cut off branches of all trees and weighed branches with needles. After that, in the field we weighed subsamples of branches with needles (at least 5% for large trees and usually > 20% for smaller trees). Each subsample was divided into needles and branches in the laboratory and then dried and weighed. Sample trees were selected to be representative of the diameter distribution—one tree from each quantile. Samples of needles (FL), branches (BR) and stems (ST, including wood and bark) were oven-dried to a constant mass (65 °C). Then, plant material was weighed with an accuracy of 1 g. Using the proportion of dry and fresh masses of samples and total fresh masses of biomass components obtained in the field, we calculated total dry mass of each biomass component for a particular model tree. As biomass of dead branches and cones strongly varies among trees, study sites and growing seasons, we decided to exclude these tree components from analyses, focusing on biomass of FL, BR, ST and their sum—aboveground biomass (AB). For each plot, we measured stand density (N), mean height weighted by basal area (Hg), growing stock volume (V) and age (A).
Data analysis
We used site-specific Naslund’s models from the lmfor::ImputeHeights() function (Mehtatalo 2008) to impute heights for each tree (R Core Team 2017). We also calculated volume of the whole stem. We decided to take into account volume of whole stems instead of merchantable volume, as the youngest trees have no merchantable volume. We also did not account for merchantable branch biomass, as it was present only in 19 of 791 sample trees and constituted a maximum of 3.4% of total stem volume. Volume of each tree stem was calculated using diameter measurements of sections 1 m in length. We assumed the shape of each section as a cylinder and the shape of the last section as a cone. Due to different origins of datasets used, we did not measure volume for 219 young sample trees (< 20 years old) and 24 older sample trees (up to 47 years old). To estimate volume of these trees, we used a machine learning technique—the random forest model (Breiman 2001) implemented in the caret::train() function (Kuhn 2008) in R software (R Core Team 2017) for obtaining tree volume, based on the diameter, height and age of the trees. We are conscious that joining datasets with measured and predicted volume undermines assumptions of methods identity. However, in our study we did not focus on tree volume estimation, but we calculated it for the purpose of calculating stand volume. Thus, we decided not to remove 54 study plots to decrease uncertainty of our models. This model had RMSE = 0.002 and R2 = 0.98, and RMSE = 0.03 and R2 = 0.98 for younger and older trees, respectively. At the stand level, we calculated Hg, but for the 35 youngest stands we calculated mean height, as diameters at breast height were not available.
In our study, we provided three methods of Scots pine biomass estimation: individual tree biomass models, stand level biomass models and stand level BCEFs. For each biomass component, we calculated nonlinear regression models, using the allometric model, as in previous biomass studies (Zianis et al. 2005; Zasada et al. 2008; Bronisz and Zasada 2016; Bronisz et al. 2016; Jagodziński et al. 2018):
where W—dry mass of the considered biomass component (kg), D—diameter (cm), H—height (m). For the youngest trees (up to 10 years old), we provided model accounting only for tree height, as the youngest trees may not reach breast height (130 cm):
Similar models were used to calculate volume of each tree within stands.
We used the provided tree-level biomass models to estimate biomass of each stand studied. In stands with A < 11 years old, we used Eq. 3 and for older stands we used Eq. 2. For stand-level biomass analyses, we calculated biomass conversion and expansion factors (BCEFs) as BCEF = W/V, where W—dry mass of the considered biomass component (Mg ha−1), obtained as a sum of tree biomass components and V—growing stock volume (m3 ha−1). For assessment of relationships between BCEFs and stand characteristics, we also used power models:
where z—stand characteristic (N, Hg, V or A), a and b—model coefficients. We used Eq. 4, with W instead of BCEF, in stand-level biomass models. To prevent lack of normality of residuals and problems with heteroscedasticity, we used iterative reweighted least squared regression implemented in the robustbase::nlrob() function (Myers 1986; Maechler et al. 2018). In this method, the regression curve is refitted in each iteration by weighting observations by the residuals. To check normality of standardized residuals and homoscedasticity, we examined diagnostic plots (standardized residuals versus fitted values). Furthermore, we compared them with volume-based functions and biomass estimations based on BCEFs. Because of variance inflation resulting from intercorrelations between predictors and problems with nonlinear regression convergence, we provided stand-level biomass models for only one independent variable. Although using multiple sample trees from multiple plots would justify application of mixed models (e.g., Repola 2009; Repola and Ahnlund Ulvcrona 2014; Bates et al. 2015), for purposes of model simplicity and applicability by practitioners we chose to use simple linear and nonlinear regression techniques. In all cases, we also calculated other measures of model quality—Akaike’s information criterion (AIC), mean error (ME), root mean squared error (RMSE) and modeling efficiency (MEf) using the following formulas:
where log—natural logarithm, \(\hat{\pi}\)—likelihood estimator of model fitness, k—number of model parameters, n—sample size, yi—ith observed dependent variable value, \(\hat{y}_{i}\)—ith predicted dependent variable value, \(\bar{y}\)—mean value of the dependent variable. Although R2 for nonlinear models is biased and does not provide the proper amount of variance explained by the models, we decided to provide this measure as rough estimations of R2 of linear models (MEf).
For model development, we used nonlinear, least-square regression using the stats::nls() function (R Core Team 2017). For comparison of model quality, we presented AIC of BCEFs and stand biomass models and AIC0—AIC of the null model (intercept only), according to Mac Nally et al. (2018). All analyses were conducted using R software (R Core Team 2017).
Results
Biomass of stands
Tree-level biomass models had coefficients of determination (MEf) ranging from 0.836 to 0.990, with an average of 0.922 ± 0.016 (Table 2). The highest values were for total aboveground biomass and stem biomass, and the lowest for branches and foliage biomass. Models based on height only, obtained for young trees (up to 10 years old) had lower accuracy than those for older trees. Total aboveground biomass of the stands studied ranged from 0.11 to 291.25 Mg ha−1, with an average of 65.62 ± 7.12. Biomass of branches ranged from 0.01 to 32.89 Mg ha−1, with an average of 9.64 ± 0.68. Biomass of needles ranged from 0.05 to 17.06 Mg ha−1, with an average of 5.43 ± 0.32. Biomass of stems ranged from 0.08 to 256.10 Mg ha−1, with an average of 53.39 ± 6.37.
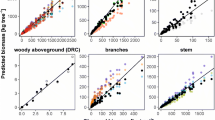
Total aboveground biomass of Scots pine stands increased with increasing stand height, growing stock volume and age, and decreased with increasing stand density (Fig. 1; Table 3). Similar trends were found for particular biomass components; however, increases in foliage and branch biomass quickly reached a plateau, with little to no increase in older stands. For total aboveground biomass and all compartments, the best model was based on stand volume (MEf from 0.322 in FL to 0.985 in ST). Other biomass components were also strongly correlated with stand height. The weakest predictor of biomass, regardless of the component considered, was stand density (MEf from 0.014 in FL to 0.633 in ST).
Relationships between stand characteristics and stand biomass components: total aboveground (AB), branches (BR), foliage (FL) and stem (ST). Parameters of nonlinear regression models are presented in Table 3
Biomass conversion and expansion factors
BCEFs of Scots pine for total aboveground biomass ranged from 0.3173 to 4.5022, with an average of 0.6207 ± 0.0423, for branch biomass from 0.0287 to 1.3933, with an average of 0.1427 ± 0.0138, for foliage biomass from 0.0087 to 1.1576, with an average of 0.1538 ± 0.0155, and for stem biomass from 0.1667 to 1.9146, with an average of 0.3984 ± 0.0201. BCEF values were constant for older stands, but in the youngest stands its values were decreasing with increasing stand age, height and growing stock volume, and increasing with increasing density (Fig. 2; Table 4). However, the rate of these dynamics was distinct only at low values of these parameters and reached a plateau after c.a. 30 years old. The best predictor of BCEFs was stand volume (MEf from − 0.044 to 0.459), except for branches where the best was stand density (MEf = 0.099). These relationships were weak; however, in most cases RMSE was lower than 0.001 Mg m−3, which was connected with low variability of BCEFs in the higher part of the range of the parameters studied. For that reason, in the older stands (above 10 years old), we may assume mean BCEFs for AB—0.4767 ± 0.00698, for BR—0.1224 ± 0.0116, for FL—0.0844 ± 0.0120 and for ST—0.3648 ± 0.0067.
Relationships between stand characteristics and BCEFs for biomass components: total aboveground (AB), branches (BR), foliage (FL) and stem (ST). Parameters of nonlinear regression models are presented in Table 4
Discussion
Effect of stand age
Our results indicated the important role of age in differing relationships between stand features and biomass, as well as BCEFs. The most distinct effect of age was found in the youngest stands, where differentiation of BCEFs and biomass was the highest. This is similar to the results of Jagodziński et al. (2017) for young stands of Betula pendula, where the estimated age breakpoint was c.a. 5 years old. In our study, there was a strong decrease in BCEFs after c.a. 10 years of stand development and after that time BCEFs were more or less constant, similar to a study focused only on young trees (Jagodziński et al. 2018). Also Schepaschenko et al. (2018) revealed this trend using a large dataset from Eurasia. This trend was confirmed for age-class-specific biomass models based on stand parameters (Fig. 3), where strong relationships occurred in the younger stands.
Distributions of deviations between biomass calculated using stand parameter biomass models (Table 3; black dots) and using BCEF models using different stand parameters (columns) multiplied by growing stock volume (Table 4; open dots) for total aboveground biomass (AB), branches (BR), foliage (FL) and stem (ST) biomass. Lines indicate 1:1 proportions
Higher variability of younger stands is connected with different conditions of juvenile growth. This may result from management treatment or site conditions. Moreover, in smaller plants, there are higher proportions of foliage and branches (Mikšys et al. 2007; Uri et al. 2012; Poorter et al. 2015), the biomass of which is less uniform than stem biomass, which constitutes most of the biomass in older trees. Foliage biomass strongly depends on different site-specific factors (Poorter and De Jong 1999; Jagodziński and Kałucka 2008; Rademacher et al. 2009); thus, its variation affects model accuracy. A similar pattern was found for BCEFs by Lehtonen et al. (2004). However, our previous paper (Jagodziński et al. 2018), where for young stands we used site-specific allometric tree-level models, showed similar patterns. Therefore, this effect is consistent regardless of the accuracy of biomass estimation method. Similarly low coefficients of determination for BCEF models were provided by Lehtonen et al. (2004). As older trees are composed mainly of stem biomass, which is strictly related to growing stock volume, this constancy may suggest using constant BCEF values for these trees. Effects of stem mass ratio may be confirmed by higher accuracy of models for BCEFs without leaves than with leaves, provided by Teobaldelli et al. (2009). Constant lines for modeled BCEFs for older Scots pines were also provided by other authors (Lehtonen et al. 2004; Jalkanen et al. 2005; Teobaldelli et al. 2009; Wojtan et al. 2011).
Effect of other stand features
In our study, the most important features influencing biomass and BCEFs were stand height and growing stock volume. These two factors are mostly related to stem biomass, which constitutes the majority of aboveground biomass (Poorter et al. 2015). As these parameters within the same age are site-dependent, we may assume that these models allow predictions to overcome site-specific conditions at the stand level and may also be better than preparing models for different site indices, which are different in particular countries. Other studies revealed high importance of site index in shaping stand biomass (e.g., Shepashenko et al. 1998; Teobaldelli et al. 2009; Schepaschenko et al. 2018). However, when we compare heteroscedasticity of models based on height and growing stock volume, those based on height seem to be more homoscedastic (Fig. 3). Stand density was the weakest predictor of stand biomass, similar to Castedo-Dorado et al. (2012). Despite its importance in shaping biomass allocation (Jagodziński and Oleksyn 2009b), its primary impact is connected with shaping growth conditions, especially single tree dimensions—at higher density individual trees have lower diameters and higher heights (Jagodziński and Oleksyn 2009a); therefore, this parameter is also included in stand height and growing stock volume.
Accuracy of models and applicability
Our study confirmed higher accuracy of tree-level than stand-level methods. Our study also showed that biomass estimation based on stand-level biomass models and BCEFs gives similar accuracy, when the best models are taken into account. However, for branch and foliage biomass, tree-stand-based models give overestimated results, and BCEFs give underestimated results, compared to biomass calculated using tree-level approaches (Fig. 3). A similar trend, but with lower magnitude of bias, was found for volume-based models. However, due to high randomness, foliage and branch biomass are the most difficult to estimate, both at the levels of trees and stands, similar to other studies (e.g., Zianis et al. 2005; Teobaldelli et al. 2009; Wojtan et al. 2011; Castedo-Dorado et al. 2012).
Regional stand-level biomass models obtained in our study may be applied in large-scale inventories, including those using airborne laser scanning and other remote sensing techniques. These inventories can easily and quickly provide large amounts of data. However, they provide the highest accuracy for height measurements (Niemi et al. 2015; Kauranne et al. 2017). For that reason, high accuracy of models based on stand height may allow for increasing applicability of these methods. Moreover, it may be used for young stands or when data on stand volume is not available, due to lack of ownership interests or remote localities (Jagodziński et al. 2017, 2018).
Conclusions
Our study provided a comprehensive set of tree- and stand-level biomass models. We also described how stand biomass increases with increasing height, growing stock volume and age, and with decreasing stand density during stand development. Our study indicated highly dynamic increases of biomass and decreases of BCEFs in the youngest phase of stand growth and relative stabilization in later phases. Our models showed that accurate biomass assessment may be conducted using airborne methods, providing data on stand height (Jagodziński et al. 2018).
References
Baskerville GL (1972) Use of logarithmic regression in the estimation of plant biomass. Can J For Res 2:49–53. https://doi.org/10.1139/x72-009
Bates D, Mächler M, Bolker B, Walker S (2015) Fitting linear mixed-effects models using lme4. J Stat Soft 67:1–48. https://doi.org/10.18637/jss.v067.i01
Bijak S, Zasada M, Bronisz A et al (2013) Estimating coarse roots biomass in young silver birch stands on post-agricultural lands in central Poland. Silva Fenn 47:963. https://doi.org/10.14214/sf.963
Breiman L (2001) Random forests. Mach Learn 45:5–32. https://doi.org/10.1023/A:1010933404324
Bronisz K, Zasada M (2016) Simplified empirical formulas to determine the dry biomass of aboveground components of trees for Scots pine. Sylwan 160:277–283
Bronisz K, Strub M, Cieszewski C et al (2016) Empirical equations for estimating aboveground biomass of Betula pendula growing on former farmland in central Poland. Silva Fenn 50:1559. https://doi.org/10.14214/sf.1559
Bussotti F, Pollastrini M, Holland V, Brüggemann W (2015) Functional traits and adaptive capacity of European forests to climate change. Environ Exp Bot 111:91–113. https://doi.org/10.1016/j.envexpbot.2014.11.006
Castedo-Dorado F, Gómez-García E, Diéguez-Aranda U et al (2012) Aboveground stand-level biomass estimation: a comparison of two methods for major forest species in northwest Spain. Ann For Sci 69:735–746. https://doi.org/10.1007/s13595-012-0191-6
Chakraborty D, Wang T, Andre K et al (2016) Adapting Douglas-fir forestry in Central Europe: evaluation, application, and uncertainty analysis of a genetically based model. Eur J For Res 135:919–936. https://doi.org/10.1007/s10342-016-0984-5
Chmura DJ, Howe GT, Anderson PD, St. Clair B (2010) Adaptation of trees, forests and forestry to climate change. Sylwan 154:587–602
Cienciala E, Černý M, Tatarinov F et al (2006) Biomass functions applicable to Scots pine. Trees 20:483–495. https://doi.org/10.1007/s00468-006-0064-4
Dyderski MK, Paź S, Frelich LE, Jagodziński AM (2018) How much does climate change threaten European forest tree species distributions? Glob Change Biol 24:1150–1163. https://doi.org/10.1111/gcb.13925
Eggleston S, Buedia L, Miwa K et al (2006) IPCC guidelines for national greenhouse gas inventories, prepared by the National Greenhouse Gas Inventories Programme. IGES, Kanagawa
Ellenberg H (1988) Vegetation ecology of central Europe. Cambridge University Press, Cambridge
Finér L, Helmisaari H-S, Lõhmus K et al (2007) Variation in fine root biomass of three European tree species: Beech (Fagus sylvatica L.), Norway spruce (Picea abies L. Karst.), and Scots pine (Pinus sylvestris L.). Plant Biosyst 141:394–405. https://doi.org/10.1080/11263500701625897
Forrester DI, Tachauer IHH, Annighoefer P et al (2017) Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. For Ecol Manag 396:160–175. https://doi.org/10.1016/j.foreco.2017.04.011
Houston Durrant T, de Rigo D, Caudullo G (2016) Pinus sylvestris in Europe: distribution, habitat, usage and threats. In: San-Miguel-Ayanz J, de Rigo D, Caudullo G et al (eds) European Atlas of forest tree species. Publication Office of the European Union, Luxembourg, pp 132–133
Hytönen J, Aro L (2012) Biomass and nutrition of naturally regenerated and coppiced birch on cutaway peatland during 37 years. Silva Fenn 46:377–394
IPCC (2013) Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Jagodziński AM, Kałucka I (2008) Age-related changes in leaf area index of young Scots pine stands. Dendrobiology 59:57–65
Jagodziński AM, Oleksyn J (2009a) Ecological consequences of silviculture at variable stand densities. I. Stand growth and development. Sylwan 153:75–85
Jagodziński AM, Oleksyn J (2009b) Ecological consequences of silviculture at variable stand densities. II. Biomass production and allocation, nutrient retention. Sylwan 153:147–157
Jagodziński AM, Jarosiewicz G, Karolewski P, Oleksyn J (2012) Carbon concentration in the biomass of common species of understory shrubs. Sylwan 156:650–662
Jagodziński AM, Kałucka I, Horodecki P, Oleksyn J (2014) Aboveground biomass allocation and accumulation in a chronosequence of young Pinus sylvestris stands growing on a lignite mine spoil heap. Dendrobiology 72:139–150. https://doi.org/10.12657/denbio.072.012
Jagodziński AM, Zasada M, Bronisz K et al (2017) Biomass conversion and expansion factors for a chronosequence of young naturally regenerated silver birch (Betula pendula Roth) stands growing on post-agricultural sites. For Ecol Manag 384:208–220. https://doi.org/10.1016/j.foreco.2016.10.051
Jagodziński AM, Dyderski MK, Gęsikiewicz K et al (2018) How do tree stand parameters affect young Scots pine biomass?—allometric equations and biomass conversion and expansion factors. For Ecol Manag 409:74–83. https://doi.org/10.1016/j.foreco.2017.11.001
Jalkanen A, Mäkipää R, Ståhl G et al (2005) Estimation of the biomass stock of trees in Sweden: comparison of biomass equations and age-dependent biomass expansion factors. Ann For Sci 62:845–851. https://doi.org/10.1051/forest:2005075
Kauranne T, Pyankov S, Junttila V et al (2017) Airborne laser scanning based forest inventory: comparison of experimental results for the Perm Region, Russia and Prior Results from Finland. Forests 8:72. https://doi.org/10.3390/f8030072
Kuhn M (2008) Building predictive models in R using the caret package. J Stat Softw 28:1–26. https://doi.org/10.18637/jss.v028.i05
Kuznetsova T, Lukjanova A, Mandre M, Lõhmus K (2011) Aboveground biomass and nutrient accumulation dynamics in young black alder, silver birch and Scots pine plantations on reclaimed oil shale mining areas in Estonia. For Ecol Manag 262:56–64. https://doi.org/10.1016/j.foreco.2010.09.030
Laiho R, Finér L (1996) Changes in root biomass after water-level drawdown on pine mires in southern Finland. Scand J For Res 11:251–260. https://doi.org/10.1080/02827589609382934
Lakida P, Nilsson S, Shvidenko A (1996) Estimation of forest phytomass for selected countries of the former European U.S.S.R. Biomass Bioenergy 11:371–382. https://doi.org/10.1016/S0961-9534(96)00030-X
Lehtonen A (2005) Estimating foliage biomass in Scots pine (Pinus sylvestris) and Norway spruce (Picea abies) plots. Tree Physiol 25:803–811. https://doi.org/10.1093/treephys/25.7.803
Lehtonen A, Mäkipää R, Heikkinen J et al (2004) Biomass expansion factors (BEFs) for Scots pine, Norway spruce and birch according to stand age for boreal forests. For Ecol Manag 188:211–224. https://doi.org/10.1016/j.foreco.2003.07.008
Lehtonen A, Palviainen M, Ojanen P et al (2016) Modelling fine root biomass of boreal tree stands using site and stand variables. For Ecol Manag 359:361–369. https://doi.org/10.1016/j.foreco.2015.06.023
Lindner M, Fitzgerald JB, Zimmermann NE et al (2014) Climate change and European forests: what do we know, what are the uncertainties, and what are the implications for forest management? J Environ Manag 146:69–83. https://doi.org/10.1016/j.jenvman.2014.07.030
Mac Nally R, Duncan RP, Thomson JR, Yen JDL (2018) Model selection using information criteria, but is the “best” model any good? J Appl Ecol. https://doi.org/10.1111/1365-2664.13060
Maechler M, Rousseeuw P, Croux C, Todorov V, Ruckstuhl A, Salibian-Barrera M, Verbeke T, Koller M, Conceicao ELT, Palma MA (2018) Robustbase: basic robust statistics R package version 0.93-3. http://CRAN.R-project.org/package=robustbase. Accessed 24 Apr 2019
Martin AR, Thomas SC (2011) A reassessment of carbon content in tropical trees. PLoS ONE 6:e23533. https://doi.org/10.1371/journal.pone.0023533
McCarthy MC, Enquist BJ (2007) Consistency between an allometric approach and optimal partitioning theory in global patterns of plant biomass allocation. Funct Ecol 21:713–720. https://doi.org/10.1111/j.1365-2435.2007.01276.x
Mehtatalo L (2008) Forest Biometrics with examples in R. Lecture notes for the forest biometrics course. http://cs.uef.fi/~lamehtat/documents/lecture_notes.pdf. Accessed 24 Apr 2019
Mikšys V, Varnagiryte-Kabasinskiene I, Stupak I et al (2007) Above-ground biomass functions for Scots pine in Lithuania. Biomass Bioenergy 31:685–692. https://doi.org/10.1016/j.biombioe.2007.06.013
Muukkonen P (2007) Generalized allometric volume and biomass equations for some tree species in Europe. Eur J For Res 126:157–166. https://doi.org/10.1007/s10342-007-0168-4
Myers R (1986) Classical and modern regression with applications. Duxbury Press, Boston
Neumann M, Moreno A, Mues V et al (2016) Comparison of carbon estimation methods for European forests. For Ecol Manag 361:397–420. https://doi.org/10.1016/j.foreco.2015.11.016
Niemi M, Vastaranta M, Peuhkurinen J, Holopainen M (2015) Forest inventory attribute prediction using airborne laser scanning in low-productive forestry-drained boreal peatlands. Silva Fenn. https://doi.org/10.14214/sf.1218
Oleksyn J, Reich PB, Chalupka W, Tjoelker MG (1999) Differential above- and below-ground biomass accumulation of European Pinus sylvestris populations in a 12-year-old provenance experiment. Scand J For Res 14:7–17. https://doi.org/10.1080/02827589908540804
Pan Y, Birdsey RA, Fang J et al (2011) A large and persistent carbon sink in the World’s forests. Science 333:988–993. https://doi.org/10.1126/science.1201609
Peichl M, Arain MA (2007) Allometry and partitioning of above- and belowground tree biomass in an age-sequence of white pine forests. For Ecol Manag 253:68–80. https://doi.org/10.1016/j.foreco.2007.07.003
Pietrzykowski M, Socha J (2011) An estimation of Scots pine (Pinus sylvestris L.) ecosystem productivity on reclaimed post-mining sites in Poland (central Europe) using of allometric equations. Ecol Eng 37:381–386. https://doi.org/10.1016/j.ecoleng.2010.10.006
Poorter H, De Jong ROB (1999) A comparison of specific leaf area, chemical composition and leaf construction costs of field plants from 15 habitats differing in productivity. New Phytol 143:163–176. https://doi.org/10.1046/j.1469-8137.1999.00428.x
Poorter H, Jagodzinski AM, Ruiz-Peinado R et al (2015) How does biomass distribution change with size and differ among species? An analysis for 1200 plant species from five continents. New Phytol 208:736–749. https://doi.org/10.1111/nph.13571
Rademacher P, Khanna PK, Eichhorn J, Guericke M (2009) Tree growth, biomass, and elements in tree components of three beech sites. In: Brumme R, Khanna PK (eds) Functioning and management of European beech ecosystems. Springer, Berlin, pp 105–136
R Core Team (2017) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna
Repola J (2009) Biomass equations for Scots pine and Norway spruce in Finland. Silva Fenn 43:625–647
Repola J, Ahnlund Ulvcrona K (2014) Modelling biomass of young and dense Scots pine (Pinus sylvestris L.) dominated mixed forests in northern Sweden. Silva Fenn 48:1190. https://doi.org/10.14214/sf.1190
Schepaschenko D, Shvidenko A, Usoltsev V et al (2017) A dataset of forest biomass structure for Eurasia. Sci Data 4:sdata201770. https://doi.org/10.1038/sdata.2017.70
Schepaschenko D, Moltchanova E, Shvidenko A et al (2018) Improved estimates of biomass expansion factors for Russian forests. Forests 9:312. https://doi.org/10.3390/f9060312
Shepashenko D, Shvidenko A, Nilsson S (1998) Phytomass (live biomass) and carbon of Siberian forests. Biomass Bioenergy 14:21–31. https://doi.org/10.1016/S0961-9534(97)10006-X
Sohngen B, Tian X (2016) Global climate change impacts on forests and markets. For Policy Econ 72:18–26. https://doi.org/10.1016/j.forpol.2016.06.011
Somogyi Z, Cienciala E, Mäkipää R et al (2007) Indirect methods of large-scale forest biomass estimation. Eur J For Res 126:197–207. https://doi.org/10.1007/s10342-006-0125-7
Teobaldelli M, Somogyi Z, Migliavacca M, Usoltsev VA (2009) Generalized functions of biomass expansion factors for conifers and broadleaved by stand age, growing stock and site index. For Ecol Manag 257:1004–1013. https://doi.org/10.1016/j.foreco.2008.11.002
Thuiller W, Lavergne S, Roquet C et al (2011) Consequences of climate change on the tree of life in Europe. Nature 470:531–534. https://doi.org/10.1038/nature09705
Uri V, Vares A, Tullus H, Kanal A (2007) Above-ground biomass production and nutrient accumulation in young stands of silver birch on abandoned agricultural land. Biomass Bioenergy 31:195–204. https://doi.org/10.1016/j.biombioe.2006.08.003
Uri V, Varik M, Aosaar J et al (2012) Biomass production and carbon sequestration in a fertile silver birch (Betula pendula Roth) forest chronosequence. For Ecol Manag 267:117–126. https://doi.org/10.1016/j.foreco.2011.11.033
Weiner J (2004) Allocation, plasticity and allometry in plants. Perspect Plant Ecol Evol Syst 6:207–215. https://doi.org/10.1078/1433-8319-00083
Wirth C, Schumacher J, Schulze E-D (2004) Generic biomass functions for Norway spruce in Central Europe—a meta-analysis approach toward prediction and uncertainty estimation. Tree Physiol 24:121–139. https://doi.org/10.1093/treephys/24.2.121
Wojtan R, Tomusiak R, Zasada M et al (2011) Trees and their components biomass expansion factors for Scots pine (Pinus sylvestris L.) of western Poland. Sylwan 155:236–243
Xie X, Cui J, Shi W et al (2016) Biomass partition and carbon storage of Cunninghamia lanceolata chronosequence plantations in Dabie Mountains in East China. Dendrobiology 76:165–174. https://doi.org/10.12657/denbio.076.016
Zasada M, Bronisz K, Bijak S et al (2008) Empirical formulae for determination of the dry biomass of aboveground parts of the tree. Sylwan 152:27–39
Zianis D, Muukkonen P, Mäkipää R, Mencuccini M (2005) Biomass and stem volume equations for tree species in Europe. The Finnish Society of Forest Science, The Finnish Forest Research Institute, Helsinki
Acknowledgements
The study was carried out under the research Project REMBIOFOR “Remote sensing based assessment of woody biomass and carbon storage in forests,” financially supported by The National Centre for Research and Development, Warsaw, Poland, under the BIOSTRATEG program (Agreement No. BIOSTRATEG1/267755/4/NCBR/2015). We also used data from the following research projects: “Environmental and genetic factors affecting productivity of forest ecosystems on forest and post-industrial habitats” (2011–2015) and “Carbon balance of the major forest-forming tree species in Poland” (2007–2011) financed by the General Directorate of State Forests, Warsaw, Poland. We kindly thank Dr. Lee E. Frelich (The University of Minnesota Center for Forest Ecology, USA) for valuable comments to the manuscript and linguistic support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Christian Ammer.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jagodziński, A.M., Dyderski, M.K., Gęsikiewicz, K. et al. Effects of stand features on aboveground biomass and biomass conversion and expansion factors based on a Pinus sylvestris L. chronosequence in Western Poland. Eur J Forest Res 138, 673–683 (2019). https://doi.org/10.1007/s10342-019-01197-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10342-019-01197-z