1 Introduction

Modelling of critical illness survival data being primary developed in the context of, e.g. health insurance contracts, also plays an important role in the currently analysed problems related to viatical market and life insurances with an accelerated death benefits option.

Critical illness insurances (CII) called also dread disease insurances (DDI) are typical examples of limited-coverage health insurance products. They provide the policyholder with a benefit in case of dread disease, which are included in a set of illnesses specified by the policy conditions such as heart attack, cancer or stroke (see Dash and Grimshaw 1993; Haberman and Pitacco 1999; Pitacco 1994, 2014). Such insurance policies can be shaped in several different ways for instance depending on the specific insurance market. The basic benefit is a lump sum benefit, which is paid on diagnosis of a specified condition, rather than on disablement. The other type of benefit consists of a set of fixed-amount benefits (annuity payments). It is worth noting that CII policy does not meet any specific needs and doesn’t protect the policyholder against such financial loss as of earnings, reimbursement of medical or other expenses incurred. The insured can use the obtained benefits for any purpose.

Nowadays, due to the growth of the secondary market, increase of interest in products providing an acceleration benefit in a situation related to terminal illness has been observed. An insured person who has a life insurance would like to use it when he has financial problems connected with health. In such situation, the easiest way of receiving financial compensation from life insurance is to withdraw from the insurance contract. Then the insurer is obliged to pay the surrender value. The insured can also sell his/her policy on the secondary market for an amount that is greater than the surrender value (and less than the death benefit). Then the viatical company takes over the payment of the insurance premiums, and in case of death of the insured, it gets the death benefits. Such agreements, called viatical settlements (see e.g. Bhuyan 2009; Gatzert 2010; Neeraj 2003), are offered to people who have developed a terminal disease. The other possibility for the insured to receive prior financial gratification is to buy a life insurance with an ADBs option that allows the insured to obtain the death benefit when he is still alive. Sometimes insurance companies allow the insured to re-buy the option of an accelerated payment of death benefits after the diagnosis of the disease. This flexibility is stimulated by the strongly growing viatical market for life insurance.

A statistical model for survival analysis is equivalent to a two-state Markov process with one direct transition from a transient alive state to an absorbing death state. This model is insufficient in framework of study and analysing the detailed life history data which occur frequently in practice, as for example in CII. In the literature, depending on the analysed problem, there have been observed two basic approaches of designing a suitable model. On the one hand, the alive state can be split into two or more transient states which, in applications, typically correspond to occurrences of various medical complications, like for example in case of an acute myocardial infarction (Hougaard and Madsen 1985) or insulin-dependent diabetes (Andersen 1988). On the other hand, the death state can be split into two or more absorbing states, which in applications typically correspond to analysing causes of death and the competing risks survival analysis. The basic model for CII (e.g. Haberman and Pitacco 1999; Pitacco 1994, 2014) combines both approaches, but does not include the specific terms of contracts offered by insurers and is not suitable for costing viatical products and life insurances with ADBs option, in particular in case of lung cancer disease.

The aim of this contribution is two-fold. In the first part we present a general multiple state model for critical illness insurances, which takes into account that a probability of death for a dread disease sufferer may depend on the duration of the disease and the payment of benefits associated with a severe disease are related to a diagnosis and the disease stage. Due to the nature of the analyzed products, we propose to split the death state in a different way than in the basic model for CII.

In order to cost insurance and viatical contract, the probabilistic structure is necessary. Then, in the second part, we focus on the modelling of the probabilistic structure of the proposed multiple state model for products associated with the risk of lung cancer which is one of the most frequently studied cancers (i.e. Diaconu et al. 2016). For determining the transition matrix related to the discrete-time Markov model, we use the methodology developed for the construction of multi-state life tables. The numerical results are based on the actual data for the Lower Silesian Voivodship in Poland. Thus we derive the transition matrix for the proposed model, which can be used to cost CII contracts, life insurances with ADBs option and viatical settlements.

The paper is organized as follows. In Sect. 2, after a brief description of the classical multiple state model for the CII, we propose a more general multiple state model for such insurances. In Sect. 3 we apply introduced in Sect. 2 a general multiple state model to the insurance against the risk of lung cancer, which is an example of the CII. Then we focus on a study of the description of the probabilistic structure of this model. Based on the actual data for the Lower Silesian Voivodship in Poland, we estimate transition probabilities for CII associated with the lung cancer in Sect. 4. In Sect. 5 we point out obtained results to possible applications in practice.

2 An actuarial model for critical illness insurance

Multiple state modelling is a stochastic tool for describing different kind of demographic problems such as: projection elderly disability (Gaag et al. 2005), analysing process of return and reentry migration (Vega and Brazil 2015) and labour-migration dynamics (Bijwaard 2014) or unemployment dynamics (Dbicka and Mazurek 2001). But the most commonly applied multistate model in biostatistics is the active-illness-death model (e.g. Bijwaard 2014; Haberman and Pitacco 1999; Pitacco 2014; Putter et al. 2007).

Following Haberman and Pitacco (1999) with a given insurance contract we assign a multiple state model. That is, at any time the insured risk is in one of a finite number of states labelled by \(1,2,\ldots ,N\) or simply by letters. Let \({{\mathcal {S}}}\) be the state space. Each state corresponds to an event which determines the cash flows (premiums and benefits). Additionally, by \({\mathcal {T}}\) we denote the set of direct transitions between states of the state space. Thus \({\mathcal {T}}\) is a subset of the set of pairs \(\left( {i,j} \right) \), i.e., \({\mathcal {T}} \subseteq \{ \left( {i,j} \right) \mid i \ne j; i,j \in {\mathcal {S}} \}\). Note that the pair \(({\mathcal {S}},{\mathcal {T}})\) is called a multiple state model, and describes all possible insured risk events as far as their evolution is concerned (usually up to the end of insurance). In this paper we consider an insurance contract issued at time 0 (defined as the time of issue of the insurance contract) and according to a plan terminating at a later time n (n is the term of policy). Moreover, let x be the age at the policy issue.

Fig. 1
figure 1

A general multiple state model for CII with benefits

Full size image

The most basic multiple state model for CII, analysed in Dash and Grimshaw (1993), has the following form

$$\begin{aligned} (\mathcal {S},\mathcal {T})=(\{a,i,d\},\{(a,i),(a,d),(i,d)\}), \end{aligned}$$

where a means that the insured is active or healthy, i indicates that the insured person is ill and suffers from a dread disease and d is related to the death of the insured. A more advanced model was investigated in Haberman and Pitacco (1999), Pitacco (1994), Pitacco (2014), where instead of a single state d, it distinguishes between death being due to dread disease d(D) and other causes d(O)

$$\begin{aligned} (\mathcal {S},\mathcal {T})=(\{a,i,d(D),d(O)\}, \{(a,i),(a,d(O)),(a,d(D))(i,d(O)),(i,d(D))\}.\nonumber \\ \end{aligned}$$
(1)

A multiple state model for such a critical illness cover is presented in Fig. 1a. Next to the arcs, benefits related to the transition between states are marked, where c is a given lump sum (death benefit), \(c^{ad}\) is an additional lump sum (disease benefit) and \(\lambda \) is the so called acceleration parameter\((0 \le \lambda \le 1)\). The amount \(c\lambda +1\mathrm{I}_{\{\lambda =0\}} c^{ad}\) is payable after the dread disease diagnosis, while the remaining amount \(c(1-\lambda )\) is payable after death, if the two random events occur within the policy term n.

Note that the multiple state model (1) covers all forms of critical illness insurances, namely

  • if \(\lambda =0\), then the model describes a rider benefit as an additional benefit,

  • if \(0< \lambda <1\), then the model describes a rider benefit as an acceleration of part of the basic life cover,

  • if \(\lambda =1\), then the model describes a stand-alone cover.

If \(\lambda =1\), the state i is absorbing, because the whole insurance cover ceases immediately after dread disease diagnosis and the payment of the sum assured (in this model direct transitions (i, d(O)) and (i, d(D)) are not present). If \(0 \le \lambda <1\), state i is irreversible.

The amount of benefits is determined in the insurance contract (at the time the contract is concluded). Costing of any insurance products is always connected with the probability structure of the model. In case of dread disease cover, data such as incidence rates of dread disease is required. A frequent problem is that the needed data is not available or only in a limited form. Therefore, one has to make assumptions, which have impact on the actuarial values such as premiums and reserves. For the CII designed in Fig. 1a, the outline of possible assumptions and methods for calculating premiums rates for a critical illness cover is presented in Dash and Grimshaw (1993). One of the objectives is to assume that the probability of death of a sick person does not depend on the duration of the disease. Moreover, the dread disease insurances are products, which are very sensitive to the development of medicine. Not all dread diseases are as mortal as some years ago and yet this type of insurances are of long-term type. Thus insurers introduce very strict conditions for the right to receive the benefit associated with a severe disease. Beside a diagnosis, the disease stage is important. This implies that the model presented in Fig. 1a is insufficient.

In this paper we propose a multiple state model for critical illness insurance, which takes into account that the probability of death for a dread disease sufferer may depend on the duration of the disease and the payment of benefits associated with a severe disease depend on a diagnosis and the disease stage.

It is important to know that critical illness benefits are paid on the diagnosis, it means to insured person who is permanently (terminally) ill. Therefore, in order to accommodate such a condition in the model of CII, state i has to be divided into two states:

\(i^D\):

the insured person is ill. In this stage the remission of the disease is still possible, although return to health state is impossible.

\(i^{DD}\):

the insured person is terminally ill. In this stage the remission of the disease is very unlikely.

After such a division a multiple state model for CII covers has a form presented in Fig. 1b where

d(O, D):

the death of the insured person who is ill or due to other cases.

d(DD):

the death of the insured person who is terminally ill.

Note that in the model presented in Fig. 1b we describe death states in a different way than in Fig. 1a. The main reason is that in described CII, values of benefits are connected with the insured’s health situation just before his death, not with the cause of death.

Moreover, the direct transition (a, d(DD)) is omitted. In particular, this means that all dread disease deaths of the terminally ill insured are represented by the state d(DD). It is a situation analogous to the one given in Fig. 1a where deaths due to dread disease are represented by the pair of transitions (a, i) and (i, d(D)), the direct transition (a, d(D)) is not possible.

Note that the term terminally ill in the context of health care refers to a person who is suffering from a serious illness and whose life is not expected to go beyond 24 months at the maximum. In practice the period of permanently illness is different for each disease. For example the HIV+ patients with more than approximately 4,5 years of life expectancy are treated as patients in relatively good health.

Let \(m_s\) be an maximum future lifetime of s-years-old terminaly ill person. We assume that \(m_s=m\) for each s-years-old terminally ill person. Moreover, it is reasonable to assume that the probability of death for a dread disease sufferer depends on the duration of the disease. To consider the influence of illness duration on the mortality probabilities, we split state \(i^{DD}\) into m states \(i^{DD(h)}\)\((h=1,2,\ldots ,m)\), where \(i^{DD(h)}\) means that the insured is terminally sick between \(h-1\) and h year (compere Amsler 1968; Gregorius 1993; Haberman and Pitacco 1999; Janssen and Manca 2006, 2007). Note that state \(i^{DD(h)}\) is a reflex state (that is strictly transitional and after one unit of time, the insured risk leaves this state). Finally, we arrive at a general multiple state model for critical illness insurances, which is presented in Fig. 1c.

3 Lung cancer as an example of dread disease

3.1 Multiple state model

After cardiovascular diseases, malignant tumors pose the second cause of death in developed countries. In particular, lung cancer belongs to the group of tumors characterized by the highest morbidity and mortality rates. It is the most frequent in population of men and the second frequent in population of women after breast cancer. Additionally, lung cancer is so-called tumour with unfavourable prognosis. For example in Poland, by analysing epidemiological data it can be concluded that only about 16% of women and 11% of men outlive five years after the diagnosis (Wojciechowska and Didkowska 2014). Because of the high prevalence and mortality rates, the relatively short survival time after the diagnosis, lung cancer is a perfect example of the deadly disease, which should be covered by critical illness insurances.

Epidemiological data confirms the existence of significant differences between the incidence of lung cancer in men and women populations. The morbidity rate is several times higher in men population. In many European countries, in the second part of the eighties of the twentieth century, the tendency of stabilizing the incidence rate is observed among men. A different situation occurs in case of women. The number of cancer cases continues to grow, which is undoubtedly caused by cultural changes, such as an increase in the number of smokers among women in the post-war generation. Due to the growing number of smokers among women, we should expect a further increase in the number of cancer cases in the population of women.

The incidence rate depends also on age (e.g. Arbeev et al. 2005a, b; Ukraintseva and Yashin 2003). Lung cancer occurs very rarely among patients up to forty years of age. The incidence begins to increase after the age of fifty. The peak incidence occurs at the sixth and seventh decades of life. By analysing geographical data, a significant diversity of incidence and mortality rates is observed in different regions of Europe. In Poland, the morbidity and mortality vary significantly among particular provinces (voivodships). Thus, age, sex and region of residence should be taken into account in the analysis of the etiology of lung cancer.

The length of life of a person suffering from lung cancer depends on his condition and in particular on whether or not he has distant metastases. Our research (based on the data set of individual hospitalizations from the Lower Silesia Department of the National Health Fund (unpublished)) shows that when the distant metastases are diagnosed, the maximum duration of sick’s life does not exceed 4 years (i.e. \(m=4\)). Besides, during these four years, the probability of survival one year is different for each of this four years. That is why in case of CII for lung cancer, the model (presented in Fig. 1c with the state space after numeration) has six states associated with health situation of the insured person which mean that the insured:

1:

is alive and not sick with malignant lung tumour (a),

2:

is diagnosed of lung cancer without metastasis to lymph nodes, brain, bones or so-called distant metastases (\(i^D\)),

3:

is suffering from cancer for a year after diagnosis of distant metastases (\(i^{DD(1)}\)),

4:

is suffering from cancer for the second year after diagnosis of distant metastases (\(i^{DD(2)}\)),

5:

is suffering from cancer for a third year after diagnosis of distant metastases (\(i^{DD(3)}\)),

6:

is suffering from cancer for a fourth after diagnosis of distant metastases (\(i^{DD(4)}\)).

Other states are associated with the death of the insured person who, before his death:

7:

was healthy or is diagnosed of lung cancer without metastasis (d(O, D)),

8:

had a lung cancer with distant metastases (d(DD)).

3.2 Probabilistic structure of the model

We focus on a discrete-time model, where insurance payments are made at the ends of time intervals (years). Let X(x, t) denote the state of an individual (the policy) at time t (\(t \in \text {T}= \{0,1,2,\dots ,n\}\)), where x is an age at entry. Hence the evolution of the insured risk is given by a discrete-time stochastic process \(\{ {X(x,t); t\in \text {T}} \}\), with values in the finite set \(\mathcal {S}=\{ 1, 2,\ldots ,8\}\). The individual’s presence in a given state or movements between states may have some financial impact like payments of premiums or benefits. Practically it means, that lump sum benefits are paid immediately before the end of the year if the process \(\{ {X(x,t); t\in \text {T}} \}\) changes the state at that year and with this changes paying such benefit is connected. Premiums are paid immediately after the beginning of the year. In order to valuate the insurance contract during n-years insurance period, the knowledge of probabilities of realizing particular cash flows is necessary.

To describe the probabilistic structure of \(\{X(x,t)\}\), for any moment \(k \in \{0,1,2,\ldots ,n \}\), we introduce vector

$$\begin{aligned} {\varvec{P}}^{[x]}(k) =\left( \mathbb {P}^{[x]}_{1}(k), \mathbb {P}^{[x]}_{2}(k), \mathbb {P}^{[x]}_{3}(k), \ldots ,\mathbb {P}^{[x]}_{8}(k)\right) ^T \in \mathbb {R}^{8}, \end{aligned}$$

where \(\mathbb {P}^{[x]}_{j}(k)=\mathbb {P}(X(x,k)=j)\). Note that \({\varvec{P}}^{[x]}(0)={\varvec{P}}(0) \in \mathbb {R}^{8}\) is a vector of the initial distribution (usually it is assumed that state 1 is an initial state, that is \( {\varvec{P}}(0) =(1,0,0,0,0,0,0,0)^T\) for each x).

Under the assumption that \(\{X(x,t)\}\) is a nonhomogeneous Markov chain, to get the sequence of matrices \(\{{\varvec{P}}^{[x]}(k)\}_{k=0}^{n}\), it is enough to know \({\varvec{P}}(0)\) and the sequence of matrices \( {\varvec{Q}}^{[x]}(0), {\varvec{Q}}^{[x]}(1),{\varvec{Q}}^{[x]}(2), \ldots , {\varvec{Q}}^{[x]}(n-1)\), where \({\varvec{Q}}^{[x]}(k)=\left( q^{[x]}_{ij}(k)\right) _{i,j=1}^{8}\) and \(q^{[x]}_{ij}(k)=\mathbb {P}(X(x,k+1)=j | X(x,k)=i)\) is a transition probability.

A transition matrix of \(\{X(x,t)\}\) for CII model given in Fig. 1c with \(m=4\) (for lung cancer disease) has the following form

$$\begin{aligned} {\varvec{Q}}^{[x]}(k)= \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} q^{[x]}_{11}(k) &{} q^{[x]}_{12}(k) &{} q^{[x]}_{13}(k) &{} 0 &{} 0 &{} 0 &{} q^{[x]}_{17}(k) &{} 0 \\ 0 &{} q^{[x]}_{22}(k) &{} q^{[x]}_{23}(k) &{} 0 &{} 0 &{} 0 &{} q^{[x]}_{27}(k) &{} 0 \\ 0 &{} 0 &{} 0 &{} q^{[x]}_{34}(k) &{} 0 &{} 0 &{} 0 &{} q^{[x]}_{38}(k) \\ 0 &{} 0 &{} 0 &{} 0 &{} q^{[x]}_{45}(k) &{} 0 &{} 0 &{} q^{[x]}_{48}(k) \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} q^{[x]}_{56}(k) &{} 0 &{} q^{[x]}_{58}(k) \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 1 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \nonumber \\ \end{aligned}$$
(2)

In the next section we provide formulas for \(q^{[x]}_{ij}(k)\).

3.3 Multiple increment–decrement tables

Transition probabilities can be determined using a multiple increment–decrement table (or multiple state life table). The number of functions of such a table is closely linked to multiple state model \((\mathcal {S}, \mathcal {T})\) (cf. Dbicka 2012; Bowers et al. 1986; Haberman 1983a, b; Jordan 1982; Mattsson 1997). The simplest multiple increment–decrement table, which refers to an x year old person is a life table \(\{l_{[x]+k}\}_{k \ge 0}\), where \(l_{[x]+k}\) is a number of those alive at the beginning of time interval \([x+k,x+k+1)\). Then \(d_{[x]+k}=l_{[x]+k}-l_{[x]+k+1}\) is the number of deaths during the time interval \([x+k,x+k+1)\). In general, one can assign for a multiple state model \((\mathcal {S}, \mathcal {T})\) and an x year old person the multiple increment–decrement table, which consists of functions described for each transient state \(i \in \mathcal {S}\):

\(l^{i}_{[x]+k}\):

denotes the number of lives in state i at age \(x + k\),

\(d^{ij}_{[x]+k}\):

the number of lives at age \(x+k\), which during period \([x+k, x+k+1)\) left the state i and transit to state j.

The following recurrence relation holds

$$\begin{aligned} l^{i}_{[x]+k+1}=l^{i}_{[x]+k} - \sum _{j:(i,j) \in \mathcal {T}} d^{ij}_{[x]+k} + \sum _{j:(j,i) \in \mathcal {T}} d^{ji}_{[x]+k}, \end{aligned}$$
(3)

where \(\sum _{j:(i,j) \in \mathcal {T}} d^{ij}_{[x]+k}\) is a number of lives, which left the state i in time interval \((x+k,x+k+1]\), and \(\sum _{j:(j,i) \in \mathcal {T}}d^{ji}_{[x]+k}\) is a number of lives, which entered state i in time interval \((x+k,x+k+1]\).

The multiple increment–decrement table

$$\begin{aligned}&\left\{ l_{[x]+k}^{1},l_{[x]+k}^{2},l_{[x]+k}^{3},l_{[x]+k}^{4},l_{[x]+k}^{5},l_{[x]+k}^{6}, d_{[x]+k}^{12}, d_{[x]+k}^{13}, d_{[x]+k}^{17}, d_{[x]+k}^{23}, d_{[x]+k}^{27}, \right. \nonumber \\&\quad \left. d_{[x]+k}^{34}, d_{[x]+k}^{38}, d_{[x]+k}^{45}, d_{[x]+k}^{48}, d_{[x]+k}^{56}, d_{[x]+k}^{58} \right\} _{k \ge 0} \end{aligned}$$
(4)

refers to an x year old person for \(({\mathcal {S}},{\mathcal {T}})\) given in Fig. 1c for lung cancer disease (i.e. with \(m=4\)). Since \(q_{68}^{[x]}(k)=1\), then \(d_{[x]+k}^{68}=l_{[x]+k}^{6}\). This is why \(d_{[x]+k}^{68}\) can be omitted in (4).

The following relations holds between elements of \({\varvec{Q}}^{[x]}(k)\) and functions of multiple increment–decrement table for \(({\mathcal {S}},{\mathcal {T}})\):

  • if i is absorbing, then

    $$\begin{aligned} q^{[x]}_{ij}(k)= \left\{ \begin{array}{l@{\quad }l} 1 &{}\mathrm{for}\,\,j=i \\ 0 &{}\mathrm{for}\,\, j \ne i \end{array} \right. , \end{aligned}$$
    (5)

  • if i is transient, then

    $$\begin{aligned} q^{[x]}_{ij}(k)= \left\{ \begin{array}{lll} \frac{l^{i}_{[x]+k+1}- \sum _{j:(i,j) \in \mathcal {T}} d^{ij}_{[x]+k}}{l^{i}_{[x]+k}} &{}\quad \mathrm{for}&{} j=i \\ \frac{d^{ij}_{[x]+k}}{l^{i}_{[x]+k}} &{}\quad \mathrm{for}&{} (i,j) \in {\mathcal {T}} \\ 0 &{}\quad \mathrm{for}&{} (i,j) \notin {\mathcal {T}} \end{array}. \right. \end{aligned}$$
    (6)

Where the numerators in (6) result directly from the recursive relation (3) and state properties. The denominators are the number of lives in state i at the beginning of k-th year of the insurance period.

The preparation of multiple increment–decrement tables for each age x is cumbersome and not always needed. In further analysis we suppose that the distribution of \(\{X(x,t)\}\) can be expressed by the distribution of process \(\{X(0,s)\}\) with regard to a 0 year old person. This assumption is known as the hypothesis of aggregation (HA), which can be equivalently formulated in several ways. Observe that, according to the model presented in Fig. 1c for \(m=4\), the alive state has been split into six transient states (i.e. states \(1,2,\ldots 6\)) and the death state has been split into two absorbing states corresponding to health situation of the insured just before his death (i.e. states 7 and 8). Then, HA for the considered model is equivalent to the condition

$$\begin{aligned} \bigwedge _{j \in \{1,2,\ldots 6\}} \mathbb {P}(X(x,k)=j)= & {} \mathbb {P}(X(0,x+k)=j \mid X(0,x) \in \{1,2,3,\ldots ,6\})\quad \quad \end{aligned}$$
(7)

for x and k that \(\mathbb {P}(X(x,k)=j)>0\).

Based on (7), it can be shown that

$$\begin{aligned} q^{[x]}_{ij}(k)= & {} \mathbb {P}(X(x,k)=j \mid X(x,k-1)=i) \\= & {} \mathbb {P}(X(0,x+k)=j \mid X(0,x+k-1)=i) \\= & {} q^{[0]}_{ij}(x+k) \end{aligned}$$

so we obtain \(\left\{ {\varvec{Q}}^{[x]}(k)\right\} ^{n-1}_{k=0}=\left\{ {\varvec{Q}}^{[0]}(x+k)\right\} ^{n-1}_{k=0}\).

In order to simplify the notation, let \(\{X(s)\}:=\{X(0,s)\}\) and for given x we have \({\varvec{Q}}(k):={\varvec{Q}}^{[0]}(x+k)\) with

$$\begin{aligned} q_{ij}(k)=\mathbb {P}(X(x+k+1)=j \mid X(x+k)=i). \end{aligned}$$

Probabilities \(q_{ij}(s)\), \(s\ge 0\) can be calculated in the same way as in (5) and (6) but using the multiple increment–decrement table

$$\begin{aligned} \left\{ l_{s}^{1},l_{s}^{2},l_{s}^{3},l_{s}^{4},l_{s}^{5},l_{s}^{6}, d_{s}^{12}, d_{s}^{13}, d_{s}^{17}, d_{s}^{23}, d_{s}^{27}, d_{s}^{34}, d_{s}^{38}, d_{s}^{45}, d_{s}^{48}, d_{s}^{56}, d_{s}^{58} \right\} _{s \ge 0} . \end{aligned}$$
(8)

Unfortunately, an appropriate set of data allowing to create the multiple increment–decrement table (8) is not always available. If so, estimation of \({\varvec{Q}}(k)\) is needed. In Sect. 4 we focus on this problem in case of lung cancer disease.

4 Estimation of transition probabilities

4.1 Data

Due to the influence of the residence place on morbidity and mortality rates of lung cancer an analysis based on data from Lower Silesia separately for men and women populations was performed. In order to estimate the transition probabilities three databases have been used.

First, in the analysis of future life time, the life tables for 2008, separately for population of men and women were used (www.stat.gov.pl/en/topics/population/life-expectancy/).

Secondly, the information about the morbidity and mortality rates is obtained on the basis of the National Cancer Registry for the Lower Silesia Region (Wojciechowska and Didkowska 2014). The register is created on the basis of individual declarations of tumors by hospitals. Note that, in the year 2008, the percentage of the declarations submitted in Lower Silesia region exceeds 95% and belongs to the best registries in Poland. Therefore, this database is reliable.

In the analysis, the data set of individual hospitalization from the Lower Silesia Department of the National Health Fund was used (unpublished). The number of patients with lung cancer was identified using the disease code (C33 and C34 according to the system of codes from ICD-10). Patients were identified using the coded numbers of the Universal Electronic System for Registration of the Population (Social Security). Data for the period from 2006 to 2011 was included in the analysis. The year 2008, as one of the middle periods, has been established as the reference year. The choice of the middle period allows to consider the histories of hospitalization of these patients in the time horizon from 2006 to 2011.

Populations of men and women are examined separately, due to a different structure of the morbidity and mortality associated with lung cancer. A data set concerning histories of hospitalization because of malignant lung cancer in 2008 in 62 hospitals was used. In the entire Lower Silesia Voivodeship, 2246 men (at age 20–94) and 945 women (at age 23–93) were hospitalized.

Since we do not know the exact date of death, we have only knowledge about a cessation of traditional treatment and the transfer of a patient to a hospice, the survival time is determined with an accuracy of a year.

4.2 Active

This section concerns probabilities associated with state 1 of the CII model i.e. probabilities of the first row of the matrix (2)

Due to (6), under HA, we obtain

$$\begin{aligned} q_{11}(k)= & {} \frac{l^{1}_{x+k}-\Big (d^{12}_{x+k}+d^{13}_{x+k}+d^{17}_{x+k}\Big )}{l^{1}_{x+k}}, \\q_{12}(k)= & {} \frac{d^{12}_{x+k}}{l^{1}_{x+k}},q_{13}(k)=\frac{d^{13}_{x+k}}{l^{1}_{x+k}} ,q_{17}(k)=\frac{d^{17}_{x+k}}{l^{1}_{x+k}}. \end{aligned}$$

Note that the probability of developing lung cancer without detected metastases can be decomposed as follows

$$\begin{aligned} q_{12}(k)=\left( {\frac{d^{12}_{x+k}+d^{13}_{x+k}}{l_{x+k}}}\right) / \left( {\frac{l^{1}_{x+k}}{l_{x+k}}}\right) -\left( {\frac{d^{13}_{x+k}}{d^{12}_{x+k}+d^{13}_{x+k}}}\right) / \left( {\frac{l^{1}_{x+k}}{d^{12}_{x+k}+d^{13}_{x+k}}}\right) \end{aligned}$$
(9)

The expression \((d^{12}_{x+k}+d^{13}_{x+k})/l_{x+k}\) (called the morbidity rate) denotes the ratio of the number of people who fell ill to the whole population. It is calculated on the basis of the crude cancer incidence rate using data from Wojciechowska and Didkowska (2014).

Let \(\zeta _{s}^{(t)}=\frac{\check{l}_{s}^{(t)}}{100{,}000}\) denote the crude cancer incidence rate for t-th year as the number of cases of illness \(\check{l}_{s}^{(t)}\) per 100,000 of the studied population at age s, calculated in five-year age groups. Because \(\zeta _{s}^{(t)}\) has significant variability, therefore we used the average of the crude cancer incidence rates

$$\begin{aligned} {\bar{\zeta }}_{s}=\frac{1}{5} \sum _{t=2006}^{2010}\zeta _{s}^{(t)}. \end{aligned}$$
(10)

It can easily be seen that the proportion of people without lung cancer and the whole population is close to one, which allows an assumption that

$$\begin{aligned} {\frac{l^{1}_{s}}{l_{s}}}\approx 1. \end{aligned}$$
(11)

Note that

$$\begin{aligned} q_{12}(k)+ q_{13}(k) = \frac{d^{12}_{x+k}+d^{13}_{x+k}}{l^{1}_{x+k}} =\frac{d^{12}_{x+k}+d^{13}_{x+k}}{l_{x+k}} \cdot \frac{l_{x+k}}{l^{1}_{x+k}} \end{aligned}$$
(12)

Putting (10) and (11) into (12) we obtain

$$\begin{aligned} q_{12}(k)+ q_{13}(k) = {\bar{\zeta }}_{x+k}. \end{aligned}$$
(13)

The estimation of \((d^{13}_{x+k})/(d^{12}_{x+k}+d^{13}_{x+k})\) required to separate a cohort of patients who, in 2008, had lung cancer diagnosed. Patients are divided into two groups. Patient with metastases during the first diagnosis belong to the first group. The second group consists of patient without metastases during the first diagnosis. Let \(\beta _{s}\) denote the percentage of s year old patients who fell ill in 2008 with the first diagnosis showing the existence of distant metastases is calculated in five-year age groups.

Then the probability (9) takes the following form [based on (13) and definition of \(\beta _{s}\)]

$$\begin{aligned} q_{12}(k)={\bar{\zeta }}_{x+k}/1-\beta _{x+k}/ {\bar{\zeta }}_{x+k}={\bar{\zeta }}_{x+k}(1-\beta _{x+k}). \end{aligned}$$
(14)

By the same argument

$$\begin{aligned} q_{13}(k)={\bar{\zeta }}_{x+k} \cdot \beta _{x+k}. \end{aligned}$$
(15)

To estimate the probability of death of a healthy person for the reason other than lung cancer, the crude cancer mortality rate \({\varpi }_{s}\) should be defined as a number of deaths \(\check{d}_{s}\) per 100,000 of the studied population at age s (calculated in five-year age groups) and can be expressed as follows

$$\begin{aligned} {\varpi }_{s}=\frac{\check{d}_{s}-d^{17}_{s}}{l_{s}}. \end{aligned}$$
(16)

Hence by (11) and (16) we arrive at

$$\begin{aligned} q_{17}(s) =\left( \frac{\check{d}_{s}}{l_{s}}-{\varpi }_{s}\right) / \left( \frac{l^{1}_{s}}{l_{s}}\right) =q_{s}-{\varpi }_{s}. \end{aligned}$$
(17)

Following the same procedure as for \(\zeta _{s}^{(t)}\), let

$$\begin{aligned} {\bar{\varpi }}_{s}=\frac{1}{5} \sum _{t=2006}^{2010}\varpi _{s}^{(t)} \end{aligned}$$
(18)

where \(\varpi _{s}^{(t)}=\frac{\check{d}_{s}^{(t)}}{100{,}000}\) is the crude rates for t-th year obtained on basis of data from Wojciechowska and Didkowska (2014). We finally obtain the following formula

$$\begin{aligned} q_{17}(k)=q_{x+k}-{\bar{\varpi }}_{x+k}, \end{aligned}$$
(19)

where \(q_{x+k}={d_{x+k}}/{l_{x+k}}\) is the probability of dying during the time interval \([x+k,x+k+1)\) calculated on the base of a life table.

Noting that the sum of the transition probabilities from a given state is equal to one, then using (14), (15) and (19) we obtain

$$\begin{aligned} q_{11}(k)=1- (q_{x+k}-{\bar{\varpi }}_{x+k})-{\bar{\zeta }}_{x+k}. \end{aligned}$$
(20)

In the second part of this section, we present methods for estimation of \({\bar{\zeta }}_{s}\), \({\beta }_{s}\) and \({\bar{\varpi }}_{s} \) for \(s=20, 21,\ldots 100\).

The average crude rates of morbidity and mortality from lung cancer estimated on the basis of raw indicators from the years 2006-2010 are shown in Table 1 (Appendix A). The rates were estimated on the basis of reports from the National Cancer Registry (Wojciechowska and Didkowska 2014).

In order to estimate the percentage of people who fell ill in 2008 and were diagnosed with metastatic disease, a cohort of patients with lung cancer who, during 2008, fell ill with lung cancer has been separated. In that year, 1353 men and 605 women were diagnosed with lung cancer in the region of Lower Silesia. Patients received one of the two diagnoses. The first option was a recognition of metastases to lymph nodes in the chest and so called distant metastases. The analysis included an additional period of four weeks after making the first diagnosis. This period, treated as the additional time which is required to obtain the results of diagnostic tests, is taken into account in the model. If, during this period, the existence of metastasis was confirmed, the patient was classified to the same group as patients who received a diagnosis of metastatic disease during the first visit. From a formal point of view, the patient moved at once from the first state to the third.

The diagnosis stating only the tumour incidence in the lungs but without metastasis was identified as the second possible type of diagnosis. In the considered model it is assumed that a patient with a diagnosis of the absence of metastasis goes into the second state.

Due to the fact that the incidence and mortality rates of lung cancer from the National Cancer Registry are presented in five-year age groups, the percentage of people diagnosed with metastases was also estimated in such groups. The patients in the age group of 20 to 40 years pose an exception. In this age group lung cancer occurs extremely rarely, therefore a twenty-year age limit was used for the estimation. On the basis of data set from Lower Silesia Department of the National Health Fund (unpublished), the percentage of patients with diagnosable metastases during the first visit is shown in Table 2 (Appendix A).

Fig. 2
figure 2

Transition probabilities from state 1 to state 2 or 3

Full size image

In Fig. 2 we present probabilities (14) and (15) with respect to age and sex of an insured person. Looking at the graphs, a significant difference in incidence between men and women can be observed. Men succumb to lung cancer several times more often than women. A different regularity is also noticeable. In the older age groups diagnosis without metastases is often posed. For women it is around 60 year of age, for men around 70. In the youngest groups, lung cancer is diagnosed with metastases. In interpreting the results, it should be remembered that the disease is considered from the point of view of a calendar year, rather than the annual individual patient’s medical history. Thus, a history of an insured person who enters the oncological health care system in January (at the beginning of a year) looks quite different from that of a patient who was diagnosed in December (at the end of a year). For this reason, the percentage of people diagnosed with metastases may appear to be lower than it might seem from the epidemiological data. The chosen method of analysis enables to take into account the fact that an insured person could potentially fall ill throughout the year since the inception of the insurance contract. In the event that this happens at the beginning of this year, the chance of occurrence of metastases is higher than when it happens at the end of the year.

Based on Polish Life Tables 2008 (www.stat.gov.pl/en/topics/population/life-expectancy/), the probabilities (19) and (20) with respect to age and sex of a person are presented in Fig. 3.

Fig. 3
figure 3

Transition probabilities from state 1 to state 7, and the probability of remaining in state 1

Full size image

4.3 Lung cancer without metastasis

Evaluating of transition probabilities for patients who were diagnosed with cancer without metastases [i.e. probabilities of the second row of the matrix (2)] is the next step of the analysis. Estimating of probabilities is associated with the analysis of the history of hospitalization of patients with lung cancer who, during the first admission in 2008, had no metastasis. Patients were hospitalized for the first time in 2006, 2007 or 2008. There is a need to define the cohort of patients, who were ill in 2006 and 2007 and at the beginning of 2008 did not have metastases as well as patients, who fell ill in 2008 without metastases as the first diagnosis. The percentage of patient who, during this year metastases were diagnosed, is calculated. The transition probability \(q_{23}(k)\) can be estimated using \(\varrho _{x+k}\), which is the proportion of patients suffering from lung cancer in 2008, who got metastases during the year and it is estimate based on Lower Silesia Department of the National Health Fund (unpublished). In further considerations, we accept that \(q_{27}(k)=q_{x+k}\). It is connected with the fact, that a sick person, who has not metastases, has a higher risk of death than a healthy person, so we also take into account the possibility of dying for one of many reasons, including lung cancer. Taking into account the above considerations, we obtain \(q_{22}(k)= 1-q_{x+k}-\varrho _{x+k}\).

Patients who, during 2008, suffered from lung cancer and in the initial diagnosis in 2008 they did not have metastases, pose the studied cohort at this stage. 1098 men and 533 women belonged to the analyzed cohorts.

In case of the second state, the examination of history of the disease from the perspective of an insurance company makes the chance of an insured person to remain without metastasis apparently higher than it results from the epidemiological data. While comparing the empirical percentages of diagnosed metastases calculated for particular years of age in a given year in populations of men and women, some differences can be spotted for both populations. In women population, the percentage of diagnosis with metastasis is highest in the age group of 45 years, then it gradually decreases. In male population it grows, reaching a peak in the age group about of 60 years, then subsides gradually. It should be noted that, in age groups with the highest lung cancer incidence rates (from 50 to 70 years), the probability of diagnosis of metastasis for a patient with determined lung cancer is higher in men population.

The chance of getting a diagnosis of metastatic is modelled using a Bernoulli distributed random variable. The parameter \(\varrho \) is defined as the success probability and is estimated using the logistic regression model. In this model, an independent variable is an age of a patient. In both populations, patients below 45 years of age occur very rarely. For this group of patients the probability of diagnosis with metastases is calculated using the nearest neighbor method. This means that the probability is constant in this group and equals the probability of diagnosis for a 45 years-old person. In female population, logistic regression model parameters were estimated for patients over 45 years of age. In the population of men, patients above 45 years of age are divided into two groups, the first form 45 to 59 years of age, and the second above 59 years of age. In these two groups, the probabilities of diagnosis with metastases are estimated using separate logistic regression models. A specified age group division ensures the best fitting of the model to the data.

The division of men population into two groups (to 59 years old and above 59 years old) has enabled obtaining the best fitted model. In case of women population any division is not necessary. A possible explanation for this phenomenon could be related to health behaviour which has influence on the probability of metastases detection. Completely different health behaviour is observed in male and female population in Poland. Women often use medical services regardless of their age. The situation is quite different for men. The men at working age are reluctant to use medical services, preventive examinations and avoid visits to doctors. Changes in health behaviour occur in pre-retirement age. Men above 59 years old are more often begin to use medical services, including preventive examinations. This phenomenon is very visible in the analysis of treatments cost in Poland. The average treatment cost for a man above 60-years old is rapidly growing and it is much higher than the average treatment cost for a woman at the same age. In case of younger groups of patients, the average treatment cost is higher for woman.

Parameter estimators of models for male and female populations are presented in Table 3 (Appendix B). The goodness of fit of model is evaluated on the basis of Wald’s test results, Lemesow Hosmer test and values of deviation. Selection of model was based on information criterion AIC. The results are presented in Table 4 (Appendix B).

Transition probabilities associated with state 2 are presented in Fig. 4. All the needed probabilities \(q_{x+k}\) were taken from Polish Life Tables 2008 (www.stat.gov.pl/en/topics/population/life-expectancy/).

Fig. 4
figure 4

Probabilities connected with state 2

Full size image

4.4 Lung cancer with metastasis

After receiving the diagnosis of metastasis, a patient is considered to be terminally ill. This section concerns probabilities associated with this situation i.e. probabilities of rows from third to sixth of the matrix (2).

Note that all state \(i=3,4,5,6\) are reflex states, then \(q_{ii}(k)=0\) and we get

$$\begin{aligned} q_{i8}(k)= & {} 1-q_{i i+1}(k). \end{aligned}$$
(21)

A person with diagnosed metastases lives no longer than four years, so \(q_{68}(k)=1\).

In particular, the estimation of \(q_{34}(k)\) (and \(q_{38}(k)\)) is equivalent to modelling of the survival time of patients, who had metastatic disease before 2008, who were diagnosed with metastatic during their first visit in 2008 or they got metastases during 2008.

Due to the low incidence rate of lung cancer with metastatic among young people between 20 and 39 years old, the probabilities associated with the states from 3 to 6 were estimated using the nearest neighbor method. Hence this probabilities are equal to probabilities calculated for 40-year old persons.

Based on analysis of the mortality of the cohort members at age \(s=40,41,\ldots ,100\), we estimate transition probabilities (21) for \(i=3,4,5\). Let us introduce a variable \(T_s\), which denotes the number of years that the s-years-old patient from the analyzed cohort survived. On the basis of empirical data Lower Silesia Department of the National Health Fund (unpublished) we assume that \(T_s\) takes values from 0 to 3. If \(T_s=0\), which means that a patient died during the first year (counting from the first hospitalization with diagnosed metastases during 2008). If \(T_s=1\), it means that a patient died during the second year et cetera. A patient survives for maximum four years.

On the basis of the probability distribution of variable \(T_s\), the transition probabilities connected with state 3 are calculated as \({q_{38}(s) =\mathbb {P}\left( T_s=0\right) }\) and

$$\begin{aligned} {q_{34}(s) =\mathbb {P}\left( T_s=1\right) +\mathbb {P}\left( T_s=2\right) +\mathbb {P}\left( T_s=3\right) .} \end{aligned}$$

On the basis of conditional probabilities, we estimate for \(i=4,5,6\) the transition probabilities to state 8 in the following way

$$\begin{aligned} q_{i8}(s) =\mathbb {P}\left( T_s=i-3\left| T_s>i-4\right. \right) =\frac{\mathbb {P}\left( T_s=i-3\right) }{1-\sum _{j=0}^{i-4}\mathbb {P}\left( T_s=j\right) }. \end{aligned}$$

Finally we obtain for male population (see Appendix C):

$$\begin{aligned} q_{38}(s)= & {} \left\{ \begin{array}{lll} 0.768485 &{}\quad \mathrm{for}&{} s \in [20,40] \\ 0.89706 r(s) &{}\quad \mathrm{for}&{} s > 40 \end{array} \right. , \end{aligned}$$
(22)
$$\begin{aligned} q_{48}(s)= & {} \left\{ \begin{array}{lll} 0.380912 &{}\quad \mathrm{for}&{} s \in [20,40] \\ \frac{0.10294 r(s)}{1-0.89706 r(s)} &{}\quad \mathrm{for}&{} s > 40 \end{array} \right. , \end{aligned}$$
(23)
$$\begin{aligned} q_{58}(s)= & {} \left\{ \begin{array}{lll} 0.953154 &{}\quad \mathrm{for}&{} s \in [20,40] \\ \frac{\frac{\exp (3.20885+0.044698s)}{1+\exp (3.20885+0.044698s)}-r(s)}{r(s)} &{}\quad \mathrm{for}&{} s > 40 \end{array} \right. , \end{aligned}$$
(24)

where \(r(s)=\frac{ \exp (0.044698s)}{1+\exp (0.044698s)}\).

Note that according to (21), the survival probabilities connected with the third to sixth states are defined by the probabilities of death.

In case of female population, the Poisson regression with identity link function is used to model the probability of survival (see Appendix C). The probabilities of death \(q_{i8}(k)\) (for \(i = 3,4,5\)) are calculated similarly to those for men and we obtain

$$\begin{aligned} q_{38}(s)= & {} \left\{ \begin{array}{lll} 0.715503 &{}\quad \mathrm{for}&{} s \in [20,40] \\ \exp (-w(s))&{}\quad \mathrm{for}&{} s > 40 \end{array} \right. , \end{aligned}$$
(25)
$$\begin{aligned} q_{48}(s)= & {} \left\{ \begin{array}{lll} 0.841937 &{}\quad \mathrm{for}&{} s \in [20,40] \\ \frac{w(s)\exp (-w(s))}{1-\exp (-w(s))} &{}\quad \mathrm{for}&{} s > 40 \end{array} \right. , \end{aligned}$$
(26)
$$\begin{aligned} q_{58}(s)= & {} \left\{ \begin{array}{lll} 0.891591 &{}\quad \mathrm{for}&{} s \in [20,40] \\ \frac{0.5w(s)^2\exp (-w(s))}{1-(1+w(s))\exp (-w(s))}&{}\quad \mathrm{for}&{} s > 40 \end{array} \right. , \end{aligned}$$
(27)

where \(w(s)=-0.005435s+0.552179\).

Fig. 5
figure 5

Probabilities of death for terminally ill persons

Full size image

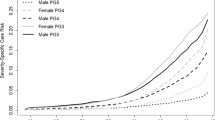
In Fig. 5 we present probabilities of death for terminally ill men (Fig. 5a) and women (Fig. 5b) with respect to age.

The statistical analyzes presented in Sect. 4 and Appendixes are carried out by means of Statistica 10.

5 Conclusions

The multiple state model presented in Sect. 2 is suitable not only for modelling the critical illness insurance contracts but also for other health insurances. It can also be adapted to insurance contracts against the loss of income due to disability or the loss of health (income protection). The introduced model allows for combining CII with life insurance. In such a combination disease benefits are usually provided as an acceleration benefit to a life insurance.

The results of Sect. 4 can be directly used to build the multiple increment–decrement tables for (proposed in Sect. 3) the multiple state model connected with lung cancer in the following form (Dbicka and Zmyślona 2016)

$$\begin{aligned} \left\{ q_{11}(s),q_{12}(s),q_{13}(s),q_{22}(s),q_{23}(s),q_{34}(s),q_{45}(s),q_{56}(s) \right\} _{s \ge 0}. \end{aligned}$$

Such tables are useful for the valuation of insurance contracts (premiums and reserves) or outflows from Health Found consisting of health-related expenses.

Death probabilities (22)–(24) and (25)–(27) concerning the population of those suffering from lung cancer with metastasis (e.g. states 3, 4, 5, 6, 8) are needed to calculate the value of viatical settlement payments (Dbicka and Heilpern 2017).