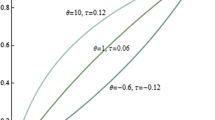Abstract
Assuming absolute continuity of marginals, we give the distribution for sums of dependent random variables from some class of Archimedean copulas and the marginal distribution functions of all order statistics. We use conditional independence structure of random variables from this class of Archimedean copulas and Laplace transform. Additionally, we present an application of our results to \({{\mathrm{VaR}}}\) estimation for sums of data from Archimedean copulas.
Similar content being viewed by others
1 Introduction
Let \(X_{1},\ldots ,X_{n}\) be absolutely continuous random variables with the marginal cumulative distribution functions (c.d.f.) \(F_{i}\) and the marginal densities \(f_{i}\), \(i=1,\ldots ,n\). The joint distribution function of \( \left( X_{1},\ldots ,X_{n}\right) \) is absolutely continuous and so is the respective copula \(C:[0,1]^{n}\rightarrow [0,1]\). Then by Sklar (1959),
for all \(\left( x_{1},\ldots ,x_{n}\right) \in \mathbb {R}^{n}\).
The random vector \((X_{1},\ldots ,X_{n})\) has Archimedean copula (Nelsen 1999) with generator \(\varphi \) if
for all \(u_{i}\in [0,1]\), \(i=1,\ldots ,n\), where \(\varphi \) is a continuous strictly decreasing function from \(\left[ 0,1\right] \) to \( [0,\infty )\) such that \(\varphi (0)=\infty \), \(\varphi (1)=0\), and the derivatives of \(\varphi ^{-1}\)of all order satisfying
for all \(u\in (0,1)\), \(i=1,2,\ldots \) . Such a function \(\varphi ^{-1}\) is called completely monotone. Then from the Bernstein theorem (Bernstein 1928) there exists a random variable \(\varTheta \ge 0\) such that \(\varphi ^{-1}\) is the Laplace transform of \(\varTheta \) (Nelsen 1999),
Additionally, we assume that
where
for \(i=1,\ldots ,n\). Under these assumptions the random variables (r.v.’s) \(X_{1},\ldots ,X_{n}\) are conditionally independent given \(\varTheta =\theta \). This is equivalent to
This construction has been presented in Marshall and Olkin (1988) and developped by Frees and Valdez (1998).
In actuarial risk management analysis it is worth considering the distribution of aggregate claims of a portfolio of single claims \( X_{1},\ldots ,X_{n}\) from an Archimedean copula, i.e.
In this way the portfolio consists of n dependent risks, where the dependence structure is defined by the Archimedean copula. In Wüthrich (2003) and Alink et al. (2004, 2005) the asymptotic distribution of (5) with an application to Value-at-Risk (\({{\mathrm{VaR}}}\)) estimation was given. More precisely if \((X_{1},\ldots ,X_{n})\) has Archimedean copula with regularly varying generator \(\varphi \) at \(0^{+}\) with index \(\alpha \), that is,
and the common marginal c.d.f. F belongs to the Fréchet domain of attraction (F is regularly varying at \(-\infty \) with index \(\beta \)), then
where the constant \(q_{n}^{F}(\alpha ,\beta )\) depends on \(F,\varphi \) only through \(\alpha \) and \(\beta \). The form of the constant \(q_{n}^{F}(\alpha ,\beta )\) for \(n>2\) is quite complicated and it is difficult to use (6) for \(n>2\). Alink et al. (2004, 2005) and Wüthrich (2003) also obtained similar results for Gumbel or Weibull extreme-value families. Using the results by de Haan and Resnick (1977), Barbe et al. (2006) extend (6) beyond Archimedean dependence structures, where \(X_{i}\) is multivariate regularly varying (for definition see Barbe et al. 2006). For Archimedean dependence structure their result agrees with (6). Our main result (Theorem 1) gives the non-asymptotic distribution of (5) for Archimedean copulas without additional restrictions on the generator \( \varphi \) and without the assumptions of identical and regular distributions of \(F_{i}\), \(i=1,\ldots ,n\). For \(n=2\) Theorem 1 is equivalent by a change of variable to the result by Cherubini et al. (2008), who proved
where \(D_{1}\) is the partial derivative with respect to the first argument and \(C_{\varphi }\) is the Archimedean copula. The distribution of (5) can also be computed numerically using the AEP algorithm (Arbenz et al. 2011). Observe that \(\mathbb {P}\left( S_{n}\le t\right) =\mathcal {P}(S(\mathbf {0},t))\), where \(\mathcal {P}\) is a probability measure on \(\mathbb {R}^{n}\) and the simplex \(S(\mathbf {0},t)\subset \mathbb {R}^{n}\) is given by \(S(\mathbf {0} ,t)=\{\mathbf {x:}\) \(x_{k}>0\) for all k and \(\sum _{k=1}^{n}x_{k}\le t\}\), for \(t>0\) and \(S(\mathbf {0},t)=\{\mathbf {x:}\) \(x_{k}\le 0\) for all k and \( \sum _{k=1}^{n}x_{k}>t\}\) for \(t<0\). In the AEP algorithm the simplex is approximated by hypercubes. Based on Theorem 1 we propose a simple Monte Carlo (MC) simulation for the calculation of this distribution (see Remarks 1, 2, 3), which may be considered as an alternative to the AEP algorithm, especially when n is large. The computation cost of the AEP algorithm for \(n\ge 6\) is very high and in practice the AEP algorithm is used for \(2\le n\le 5\) (see Arbenz et al. 2011, p. 577). Another profit of our non-asymptotic approach in comparison to the asymptotic results can be seen in Sect. 4.2 (see Figs. 1, 2, Remark 5 and Final Conclusions), where we consider the problem of \({{\mathrm{VaR}}}\) estimation for sums of Archimedean copulas.
In the following, we consider the distribution of order statistics for Archimedean copulas. The characterization of this distribution has been also given in (Jaworski and Rychlik 2008). Let \(X_{1:n}\le \cdots \le X_{n:n}\) be order statistics. Following David and Nagaraja (2003) and Galambos (1982), we write the distribution function of the mth order statistic \(X_{m:n}\) from the sample as
If \(X_{1},\ldots ,X_{n}\) are exchangeable, then
Applying (1) to (7), we obtain the distribution function of the order statistics for Archimedean copulas (see Proposition 1). When \( X_{1},\ldots ,X_{n}\) are independent and identically distributed (i.i.d.) with common c.d.f. F, then we have a well-known formula for the c.d.f. of the mth smallest order statistic:
In Sect. 4 we present \({{\mathrm{VaR}}}\) estimation for sums of Archimedean copulas using the distribution of the maximum of r.v.’s. from Archimedean copulas [lower confidence intervals for \({{\mathrm{VaR}}}\) with examples and asymptotic behavior for small quantiles (Lemma 1), where the marginal distribution is subexponential (Goldie and Klüppelberg 1998)]. Using conditional independence for r.v.’s from Archimedean copulas, in the case where the marginal distribution is subgaussian, in Lemma 2 we obtain an exponentional inequality for large deviations for sums of Archimedean copulas.
2 Distribution for sums for Archimedean copulas
In this section we consider the distribution for sums for Archimedean copulas. The asymptotic distribution of such sums under some technical assumptions was given in Alink et al. (2004, 2005) and Wüthrich (2003). Let \( S_{n}=\sum _{i=1}^{n}X_{i}\).
Theorem 1
If \(X_{1},\ldots ,X_{n}\) come from an Archimedean copula (1)–(4), then for all \(n\ge 2\),
(if the integral exists) where \(s_{n-1}(t)=\sum \nolimits _{i=1}^{n-1}\varphi \left( F_{i+1}\left( u_{i}\right) \right) +\varphi \left( F_{1}\left( t-\sum \limits _{i=1}^{n-1}u_{i}\right) \right) \), \(\left( \varphi ^{-1}(s)\right) ^{\left( n-1\right) }=\frac{d^{n-1}}{du^{n-1}}\varphi ^{-1}(s)\) and \( f_{i}=F_{i}^{^{\prime }}\).
Proof
First, we prove that for all \(n\ge 2\),
Assuming (10) is true for \(n-1\) and using the fact that \(S_{n-1}\) and \(X_{n}\) are conditionally independent given \(\varTheta =\theta \), and
we obtain
Then by induction, we have (10). Using (10), we obtain
Obviously, the relation
now yields (9).
Popular Archimedean copulas such as the Gumbel and Clayton copulas can be derived from the construction (2)–(4) [see Marshall and Olkin 1988]. Remarks 1, 2, 3 below are devoted to the numerical computation of (9).
Remark 1
If we simulate N times \(n-1\) independent variables \(U_{i}^{j}=u_{i}^{j}\) for \(i=1,\ldots ,n-1\) and \(j=1,\ldots ,N\) from the distribution of density \(f_{i+1}\), then MC calculation of (9) yields
where \(H_{n}\left( x\right) =\left( \varphi ^{-1}(s)\right) ^{\left( n-1\right) }|_{s=x}\).
Observe that, for the case of the Clayton copula, the probability \(\mathbb {P} \left( S_{n}\le t\right) \) is given by the following simple formula.
Corollary 1
For the Clayton copula with \(\varphi ^{-1}(t)=\left( 1+\alpha t\right) ^{- \frac{1}{\alpha }}\) for \(\alpha >0\), we have, for all \(n\ge 2\),
if the integral exists.
Proof
For the Clayton copula with parameter \(\alpha \), we have \(\varTheta \sim \varGamma \left( \frac{1}{\alpha },\alpha \right) \) and \(\varphi (p)=\frac{1}{ \alpha }\left( p^{-\alpha }-1\right) \), \(\varphi ^{^{\prime }}(p)=-p^{-\alpha -1}\) and
Therefore, from (12), we get (13).
Remark 2
For the Clayton copula, if we simulate N times \(n-1\) independent variables \(U_{i}^{j}=u_{i}^{j}\) for \(i=1,\ldots ,n-1\) and \(j=1,\ldots ,N\) from the distribution of density \(f_{i+1}\), then MC calculation of (13) yields
Remark 3
For the Gumbel copula with \(\alpha \ge 1\) from Remark 1 one may observe that if we simulate N times \(n-1\) independent variables \( U_{i}^{j}=u_{i}^{j}\) for \(i=1,\ldots ,n-1\) and \(j=1,\ldots ,N\) from the distribution of density \(f_{i+1}\), then MC calculation of (9) yields
(a)
(b)
(c)
where \(w_{j}^{n}(t):=\sum \limits _{i=1}^{n}\varphi \left( F_{i+1}\left( u_{i}^{j}\right) \right) +\varphi \left( F_{1}\left( t-\sum \limits _{i=1}^{n}u_{i}^{j}\right) \right) \) for \(n=1,2,3\) and \(\varphi (x)=\left( \ln \left( 1/x\right) \right) ^{\alpha }\).
From Theorem 1 and Corollary 1 we have simple formulas for the distribution of (5) for \(n=2\).
Corollary 2
-
(a)
For the Clayton copula with parameter \(\alpha >0\),
$$\begin{aligned} \mathbb {P}\left( S_{2}\le t\right) =\frac{\alpha \varGamma \left( 1+\frac{1}{\alpha } \right) }{\varGamma \left( \frac{1}{\alpha } \right) }\int \limits _{-\infty }^{\infty }\frac{ \left( F_{2}(u)\right) ^{-\alpha -1}f_{2}(u)}{\left( \left( F_{2}(u)\right) ^{-\alpha }+\left( F_{1}(t-u)\right) ^{-\alpha }-1\right) ^{1+\frac{1}{\alpha } }}du \text {.} \end{aligned}$$ -
(b)
For the Gumbel copula with parameter \(\alpha \ge 1\),
$$\begin{aligned} \mathbb {P}\left( S_{2}\le t\right) =-\frac{1}{\alpha }\int \limits _{-\infty }^{\infty }e^{-\left( w(t)\right) ^{\frac{1}{\alpha } }}\left( w(t)\right) ^{-1+\frac{1}{\alpha } }\frac{1}{F_{2}(u)}\left( \ln \left( \frac{1}{F_{2}(u)}\right) \right) ^{\alpha -1}f_{2}(u)du\text {,} \end{aligned}$$where \(w(t)=\varphi \left( F_{2}(u)\right) +\varphi \left( F_{1}(t-u)\right) \) and \(\varphi (x)=\left( \ln \left( 1/x\right) \right) ^{\alpha }\). In both formulas it is assumed that the integrals exist.
3 Order distributions for Archimedean copulas
Our main result in this section is
Proposition 1
If \(X_{1},\ldots ,X_{n}\) come from an Archimedean copula (1)–(2), then
When \(X_{1},\ldots ,X_{n}\) are identically distributed with marginal c.d.f. F, then
Proof
Straightforward from (7).
Therefore, we get immediately
Corollary 3
-
(i)
For the Gumbel copula with \(\varphi ^{-1}(t)=\exp \left( -t^{\frac{1}{ \alpha }}\right) \) for \(\alpha \ge 1\), we have
$$\begin{aligned} \mathbb {P}\left( X_{m:n}\le x\right) =\sum _{j=m}^{n}\left( -1\right) ^{j-m} \genfrac(){0.0pt}1{j-1}{m-1}\genfrac(){0.0pt}1{n}{j}\exp \left( -\left( \sum _{i=1}^{j}\left( \ln \left( \frac{1}{F_{i}(x)}\right) \right) ^{\alpha }\right) ^{\frac{1}{\alpha }}\right) \text {.} \end{aligned}$$When \(X_{1},\ldots ,X_{n}\) are identically distributed with marginal c.d.f. F, then
$$\begin{aligned} \mathbb {P}\left( X_{m:n}\le x\right) =\sum _{j=m}^{n}\left( -1\right) ^{j-m} \genfrac(){0.0pt}1{j-1}{m-1}\genfrac(){0.0pt}1{n}{j}\left( F(x)\right) ^{j^{\frac{1}{\alpha }}}\text {.} \end{aligned}$$ -
(ii)
For the Clayton copula with \(\varphi ^{-1}(t)=\left( 1+\alpha t\right) ^{-\frac{1}{\alpha }}\) for \(\alpha >0\), we have
$$\begin{aligned} \mathbb {P}\left( X_{m:n}\le x\right) =\sum _{j=m}^{n}\left( -1\right) ^{j-m} \genfrac(){0.0pt}1{j-1}{m-1}\genfrac(){0.0pt}1{n}{j}\left( 1+\sum _{i=1}^{j}\left( \left( F_{i}(x)\right) ^{-\alpha }-1\right) \right) ^{-\frac{1}{\alpha }}\text {.} \end{aligned}$$
When \(X_{1},\ldots ,X_{n}\) are identically distributed with marginal c.d.f. F, then
4 Applications
We consider the problem of interval estimation for \({{\mathrm{VaR}}}\) for sums of n identically distributed random variables from Archimedean copulas. Denote\({{\mathrm{VaR}}}_{\gamma }(S_{n}):=D_{n}^{-1}(\gamma )\), where \(D_{n}\) is the distribution function of \(S_{n}\) given by (5).
4.1 Lower confidence intervals for \({{\mathrm{VaR}}}\)
In practice we are often interested in finding a level \(c_{\delta }\) such that
for some large \(\delta \). This is equivalent to \(\mathbb {P}\left( S_{n}\le c_{\delta }\right) =1-\delta \) and \(c_{\delta }\) is a quantile of small order \(1-\delta \). Hence, we wish to estimate \({{\mathrm{VaR}}}_{\gamma }(S_{n})\) for small \(\gamma \).
From the lower bound for \({{\mathrm{VaR}}}\) for sums of dependent variables in (Mesifioui and Quessy 2005, Remark 3.3), we know that for all \(\gamma \le F(x^{*})\),
where F is the marginal c.d.f. of \(X_{i}\), \(i=1,\ldots ,n\), and we assume that \(f(x)=dF(x)/dx\) is non-decreasing for all \(x\le x^{*}\) for some fixed point \(x^{*}\) (for example a unimodal distribution with mode at \( x^{*}\)). We build a lower confidence interval for \({{\mathrm{VaR}}}_{\gamma }(S_{n})\) in the form
where \(1-\beta \) is the confidence coefficient. From (16) it is sufficient to find r such that
By (15), note that
Below we list max r satisfying (17) for the Gumbel and Clayton copulas for small \(\gamma \) for a few parameters \(\alpha \) for a unimodal marginal c.d.f. F.
Remark 4
In real applications, we often do not know the function \(\varphi \), or if we know the formula of \(\varphi \), we do not know the parameters of this function. Hence, we must estimate \(\varphi \) or its parameters. Let \(\hat{ \varphi }\) be an estimator of \(\varphi \) (nonparametric if \(\varphi \) is unknown or parametric if only a formula of \(\varphi \) is known). Then, by replacing \(\varphi \) with \(\hat{\varphi }\) in (17), we obtaine an estimator of the lower confidence interval for \({{\mathrm{VaR}}}_{\gamma }(S_{n})\).
4.2 Bound for large losses for sums of Archimedean copulas
In this subsection we assume that the losses of a portfolio of n assets are given by \(\tilde{S}_{n}=-\sum _{i=1}^{n}X_{i}\), where \(X_{i}\ge 0\) and come from Archimedean copulas (2)–(4). We search for \( t_{\gamma }>0\) such that
for some small \(\gamma >0\).
Below, we consider two cases. The first is when the marginal c.d.f. F is subexponential (e.g. heavy tailed), and the second when F is subgaussian.
A c.d.f. F supported on \([0,\infty )\) belongs to the subexponentional class \(\mathcal {S}\) if for some (equivalently, all) \(n\ge 2\),
where \(f(x)\sim g(x)\) means \(\lim _{x\rightarrow \infty }\frac{f(x)}{g(x)}=1\) , \(\bar{F}(x)=1-F(x)\), and \(F^{*n}\) is the n-fold convolution of F. Obviously for i.i.d. \(X_{1},\ldots ,X_{n}\) we have \(\bar{F}^{*n}(x)= \mathbb {P}\left( X_{1}+\ldots +X_{n}>x\right) \).
Lemma 1
If \(F\in \mathcal {S}\), \(X_{i}\) for \(i=1,\ldots ,n\) are non-negative and come from Archimedean copulas (2)–(4), then for all \(n\ge 2\),
Proof
Since \(X_{1},\ldots ,X_{n}\) are independent given \(\varTheta =\theta \), from the fact that \(F\in \mathcal {S}\) (see Goldie and Klüppelberg 1998) we have
Since \(\mathbb {P}\left( \max _{1\le i\le n}X_{i}>nt\mid \varTheta =\theta \right) >0\) for all \(\theta >0\), we may write
Consequently, from (15), we have \(\mathbb {P}\left( \max _{1\le i\le n}X_{i}>nt\right) =\mathbb {P}\left( X_{n:n}>nt\right) =1-\varphi ^{-1}\left( n\varphi \left( F\left( nt\right) \right) \right) \). Therefore, we obtain ( 19).
From (19) we may find \(t_{\infty }\) such that \(\mathbb {P}\left( \tilde{ S}_{n}\le -nt_{\infty }\right) =\mathbb {P}\left( S_{n}\ge nt_{\infty }\right) =\gamma \), namely
Remark 5
If \(\mathbb {P}(X_{i}>x)=L(x)x^{-\alpha }\) for \(\alpha >0\), for \(i=1,\ldots ,n \), where L is a slowly varying function as \(x\rightarrow \infty \), then \(F\in \mathcal {S}\) (see Goldie and Klüppelberg 1998) and we may apply formulas (19)–(20) for the marginal Pareto distribution where \(\mathbb {P}(X_{i}>x)=\left( \frac{\theta }{x}\right) ^{\beta }\), \(\theta \), \(\beta >0\). In the case when the Archimedean generator \(\varphi \) is regularly varying with index \( -\alpha \) at all x (\(\lim _{y\rightarrow x}\frac{F(yt)}{F(y)}=t^{-\alpha }\) for all \(t>0\)), Wüthrich (2003) showed that
where \(q_{n}^{F}\left( \alpha ,\beta \right) \) is some constant depending on \(\varphi \) and F [see (6)]. For \(n>2\) it is very difficult to calculate \(q_{n}^{F}\left( \alpha ,\beta \right) \) directly. If \(n=2\) and the marginal distribution of \(-X_{i}\) is the Pareto distribution with parameters \(\theta ,\beta \), and \(\varphi \) is regularly varying with index \( -\alpha \) for \(\alpha =1/\beta \), then \(q_{n}^{F}\left( \alpha ,\beta \right) =(1/2)^{\beta }(1+\beta )\). If we set \(\beta =2\), then \(t_{W}\) such that \(\mathbb {P}\left( \tilde{S}_{n}\le -nt_{W}\right) \sim (1/2)^{\beta }(1+\beta )\left( \frac{\theta }{t_{W}}\right) ^{\beta }=\gamma \) is given by the formula
For the Clayton copula with \(\alpha =1/2\) (regularly varying with index \( -\alpha \)) and F the c.d.f. of the Pareto distribution with parameters \( \theta \) and \(\beta =2\), from (20) we obtain
In Fig. 1 we see \(t_{_{W}}\) and \(t_{\infty }\) for \(\theta =5\), \(\beta =2\) as functions of \(\gamma \in (0,0.0025)\). Additionally we indicate \(t_{*}\) corresponding to \(\mathbb {P}(S_{2}\ge 2t_{*})=\gamma \), where the c.d.f. of \(S_{2}\) is calculated from \(N=1000\) MC simulation based on Remark 2 from the Clayton copula with \(\alpha =1/2\) and marginal Pareto distribution with \(\theta =5\) and \(\beta =2\).
We say that a r.v. X is subgaussian (more precisely, b-subgaussian) if there is some \(b>0\) such that for every \(t\in \mathbb {R}\) one has \(\mathbb {E} e^{tX}\le e^{b^{2}t^{2}/2}\).
Lemma 2
If the marginal distributions of \(X_{i}\) are b-subgaussian, non-negative for \(i=1,\ldots ,n\) and come from Archimedean copulas (2)–(4), then for all \(n\ge 2\) and any \(t>0\),
Proof
From the Markov inequality for every \(x>0\),
Since \(X_{1},\ldots ,X_{n}\) are independent given \(\varTheta =\theta \), we have
From the fact that \(\left( \mathbb {E}\left( e^{xX_{1}}\mid \varTheta =\theta \right) \right) ^{n}\le \mathbb {E}\left( e^{nxX_{1}}\mid \varTheta =\theta \right) \), we obtain
and since \(X_{1}\) is b-subgaussian,
Let \(G(x)=e^{-ntx+b^{2}x^{2}n^{2}/2}\). By standard calculation we find that G has global minimum \(x_{\min }=\frac{t}{b^{2}n}\), and \(G(x_{\min })=\exp \left( - \frac{t^{2}}{2b^{2}}\right) \), which yields (22).
As a consequence of (22) we may find \(t_{\gamma }\) satisfying (18 ), because \(\mathbb {P}\left( \tilde{S}_{n}\le -nt_{\gamma }\right) =\mathbb {P}\left( S_{n}\ge nt_{\gamma }\right) \le \exp \left( -\frac{t_{\gamma }^{2}}{2b^{2}} \right) \le \gamma \). Hence \(t_{\gamma }\ge b\sqrt{2\ln \left( \frac{1}{\gamma } \right) }\). In this case Wüthrich (2003) showed that if \(X_{1}\), \(X_{2}\) have the standard normal distribution with Archimedean generator \(\varphi \) regularly varying with index \(-1\), then
as \(t\rightarrow \infty \). In Fig. 2 we see \(t_{\gamma }\), \(t_{W}\) from (23) as functions of \(\gamma \in (0,0.0025)\), and \(t_{*}\) corresponding to \(\mathbb {P}(S_{2}\ge 2t_{*})=\gamma \), where the c.d.f. of \(S_{2}\) is calculated from \(N=1000\) MC simulations based on Remark 2 from the Clayton copula with \(\alpha =1\) and marginal standard normal distribution.
Final Conclusions We have obtained simple formulas for distributions for order statistics from Archimedean copulas, and the formulas have been applied to construct non-parametric confidence intervals for \({{\mathrm{VaR}}}\) for sums for Archimedean copulas. From Tables 1, 2 we can see that the lower bound of the confidence interval for \({{\mathrm{VaR}}}\) for the Gumbel copula is decreasing when the parameter \(\alpha \) is increasing. For the Clayton copula the lower bound of the confidence interval for \({{\mathrm{VaR}}}\) is almost constant when \(\alpha \) is increasing.
Based on Fig. 1, if the marginal distribution F is Pareto for the Clayton copula for \(\alpha =1/2\), then \({{\mathrm{VaR}}}_{\gamma }\left( S_{2}\right) \) for very small \(\gamma \) is more overestimated when we use the asymptotic formula (21) of Wüthrich (2003) than if we use the formula from our Lemma 1. If the marginal distribution F is standard normal and we consider the Clayton copula for \(\alpha =1\), then from Fig. 2 we see that \({{\mathrm{VaR}}}_{\gamma }\left( S_{2}\right) \) for very small \(\gamma \) is overestimated from formula (23) by Wüthrich (2003) and underestimated by the formula from our Lemma 2. In Theorem 1 we gave the distribution of \(S_{n}\) and this exact distribution simulated from MC samples was useful for the evaluation of the asymptotic distribution of \(S_{n}\) obtained by Wüthrich (2003) and in our Lemmas 1, 2.
References
Alink S, Löwe M, Wüthrich MV (2004) Diversification of aggregate dependent risks. Insur Math Econ 35:77–95
Alink S, Löwe M, Wüthrich MV (2005) Analysis of the expected shortfall of aggregate dependent risks. ASTIN Bull 35:25–43
Arbenz P, Embrechts P, Puccetti G (2011) The AEP algorithm for the fast computation of the distribution of the sum of dependent random variables. Bernoulli 17(2):562–591
Barbe P, Fougères A-L, Genest C (2006) On the tail behaviour of sums of dependent risks. ASTIN Bull 36:361–373
Bernstein SN (1928) Sur les fonctions absolument monotones. Acta Math 52:1–66
Cherubini U, Mulinacci S, Romagnoli S (2008) Copula based martingale processes and financial prices dynamics. Working paper (2008)
David HA, Nagaraja HN (2003) Order statistics, 3rd edn. Wiley, Hoboken
de Haan L, Resnick SI (1977) Limit theory for multidimensional sample extremes. Z Wahr Geb 40:317–337
Frees EW, Valdez EA (1998) Understanding relationships using copulas. N Am Actuar J 2:1–25
Galambos J (1982) The role of exchangeability in the theory of order statistics. In: Koch G, Spizzichino F (eds) Exchangeability in probability and statistics. North-Holland, Amsterdam, pp 75–87
Goldie Ch M, Klüppelberg C (1998) Subexponential distributions. In: Adler R, Feldman R, Taqqu MS (eds) A practical guide to heavy tails: statistical techniques for analysing heavy tailed distributions. Birkhäuser, Boston, pp 453–459
Jaworski P, Rychlik T (2008) On distributions of order statistics for absolutely continuous copulas with applications to reliability. Kybernetika 44:757–776
Marshall AW, Olkin I (1988) Families of multivariate distributions. JASA 83:834–841
Mesifioui M, Quessy J-F (2005) Bounds on the value-at-risk for sum of possibly dependent risks. Insur Math Econ 37:135–151
Nelsen RB (1999) An introduction to copulas. (Lecture Notes in Statistics 139) Springer, New York
Sklar A (1959) Fonctions de répartition à n dimensions et leurs marges. Publ Inst Stat Univ Paris 8:229–231
Wüthrich MV (2003) Asymptotic value-at-risk estimates for sums of dependent random variables. ASTIN Bull 33:75–92
Acknowledgments
I would like to thank the Associate Editor and two referees for their helpful constructive comments which helped me to improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Furmańczyk, K. Archimedean copulas with applications to \({{\mathrm{VaR}}}\) estimation. Stat Methods Appl 25, 269–283 (2016). https://doi.org/10.1007/s10260-015-0326-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-015-0326-7