Contraction of collecting lymphatics: organization of pressure-dependent rate for multiple lymphangions

Abstract

The paper describes the extension of a previously developed model of pressure-dependent contraction rate to the case of multiple lymphangions. Mechanical factors are key modulators of active lymphatic pumping. As part of the evolution of our lumped-parameter model to match experimental findings, we have designed an algorithm whereby the time until the next contraction depends on lymphangion transmural pressure in the contraction just completed. The functional dependence of frequency on pressure is quantitatively matched to isobaric contraction experiments on isolated lymphatic segments. When each of several lymphangions is given this ability, a scheme for their coordination must be instituted to match the observed synchronization. Accordingly, and in line with an experiment on an isolated lymphatic vessel segment in which we measured contraction sequence and conduction delay, we took the fundamental principle to be that local timing can be overridden by signals to initiate contraction that start in adjacent lymphangions, conducted with a short delay. The scheme leads to retrograde conduction when the lymphangion chain is pumping against an adverse pressure difference, but antegrade conduction when contractions occur with no or a favourable pressure difference. Abolition of these conducted signals leads to chaotic variation of cycle-mean flow-rate from the chain, diastolic duration in each lymphangion, and inter-lymphangion delays. Chaotic rhythm is also seen under other circumstances. Because the model responds to increasing adverse pressure difference by increasing the repetition rate of contractions, it maintains time-average output flow-rate better than one with fixed repetition rate.

Appendices

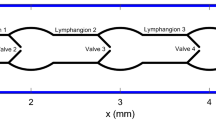
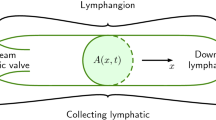
Appendix 1: Equations for n lymphangions with inlet/outlet pipette resistance

Mass conservation: $\frac{dD_i }{dt}=\frac{D_i ^{3}}{32\,\upmu L^{2}}\left( {p_{1,i} -2p_{{\mathrm{m},}i} +p_{2,i} } \right)$, for $i=1$ to n; D, diameter; t, time; $\mu$, viscosity; L, lymphangion length; p, pressure; and suffices 1, m and 2 denote the upstream end, mid–point, and downstream end of a lymphangion.⁵

Momentum conservation: $p_{1,i} -p_{{\mathrm{m},}i} =\frac{64\,\upmu L}{\pi D_i ^{4}} \frac{p_{2,i-1} -p_{1,i} }{R_{\mathrm{V}} \left( {p_{2,i-1} ,p_{1,i} ;p_{\mathrm{e}} } \right) }$,

and $p_{{\mathrm{m},}i} -p_{2,i} =\frac{64\upmu L}{\pi D_i ^{4}}\frac{p_{2,i} -p_{1,i+1} }{R_{\mathrm{V}} \left( {p_{2,i} ,p_{1,i+1} ;p_{\mathrm{e}} } \right) }$, where

$R_{{\mathrm{V},}i} =R_{{\mathrm{Vn}}} +\frac{R_{{\mathrm{Vx}}} }{1+\exp \left[ {-s_{\mathrm{o}} \left( {\Delta p_{{\mathrm{V},}i} -\Delta p_{{\mathrm{o},}i} } \right) } \right] },$ with $\Delta p_{{\mathrm{V},}i} =p_{2,i-1} -p_{1,i}$;

$R_{\mathrm{V}}$, valve resistance; $R_{\mathrm{Vn}}$, minimum valve resistance; $R_{\mathrm{Vx}}+R_{\mathrm{Vn}}$, maximum valve resistance; $s_{\mathrm{o}}$, a constant defining the rate of transition. The open/close threshold $\Delta p_{{\mathrm{o},}i}$ is a nonlinear function of $p_{2,i-1} -p_{\mathrm{e}}$ when closed, and of $p_{1,i} -p_{\mathrm{e}}$ when open; see Bertram et al. (2014b).

For $i=1$ only, $p_{2,i-1} =p_{2,0} =p_{\mathrm{a}} -R_{\mathrm{a}} \frac{p_{2,0} -p_{1,1} }{R_{{\mathrm{V},}1} }$; for $i=n$ only, $p_{1,i+1} =p_{\mathrm{b}} +R_{\mathrm{b}} \frac{p_{2,n} -p_{1,n+1} }{R_{{\mathrm{V},}n+1} }$; $p_{\mathrm{a}}$ and $p_{\mathrm{b}}$ are the pressures in the up- and downstream reservoirs, and $R_{\mathrm{a}}$ and $R_{\mathrm{b}}$ are the resistances of the up- and downstream micropipettes cannulating the vessel segment, respectively.

Constitutive relations: the passive and maximally contracted states are defined by the curves $D_{i,{\mathrm{psv}}} =f_{\mathrm{psv}} \left( {\Delta p_{\mathrm{tm,}i} } \right)$ and $D_{i,\mathrm{act}} =f_{\mathrm{act}} \left( {\Delta p_{\mathrm{tm,}i} } \right)$, respectively, where $\Delta p_{\mathrm{tm,}i} =p_{\mathrm{m,}i} -p_{\mathrm{e}}$; see Bertram et al. (2017). A contraction consists of smooth evolution of the $D_i \left( {\Delta p_{\mathrm{tm,}i} } \right)$-relation between these extremes governed by $D_i =D_{i,\mathrm{psv}} -M\left( t \right) \left[ {D_{i,\mathrm{psv}} -D_{i,\mathrm{act}} } \right]$, where the time-course of active contraction $M\left( t \right)$ is calculated as detailed by Bertram et al. (2017); at its simplest, it is an inverted cosine wave with frequency f and duration 1 / f.

Pressure-dependent diastolic duration: the period of relaxation between systoles (in the absence of activation signals conducted from other lymphangions) is calculated at each instant of end-systole as $\Delta t_{\mathrm{r,}i} =\frac{1}{f_{\mathrm{tw,}i} }-\frac{1}{f}$, where $f_{\mathrm{tw,}i} =60y_i$, with $y_i =-\,1.39q_i ^{2}+12.6q_i +0.647$, $q_i =\ln \left( {1+x_i } \right)$, and $x=f\int _{t_\mathrm{c} }^{t_\mathrm{c} +1/f} {\Delta p_{\mathrm{tm},i} } dt$ is the average transmural pressure (in $\mathrm{cmH}_{2}\hbox {O}$) over the preceding systole starting at time ${{ t}}_{\mathrm{c}}$; see Bertram et al. (2017).⁶

Appendix 2: Numerical scheme for organizing contraction times

Two vectors are maintained throughout the simulation, each of length equal to the number of lymphangions plus two (i.e. including the two part-lymphangions at the ends).

The first vector, say $s_{\mathrm{old}}$, contains the times at which each lymphangion last began contraction. The second, say $s_{\mathrm{new}}$, contains the most up-to-date information about the times at which each lymphangion will next start contraction. The algorithm is as follows:

• 1. Initialize: at $t = t_{0}$, all lymphangions start contracting, so set the vector elements $s_{\mathrm{old}}(i)= t_{0}$ for all i. Set $s_{\mathrm{new}}(i)=t_{\mathrm{large}}$ for all i, where $t_{\mathrm{large}}$ is some large positive value greater than the maximum time in the full simulation.

• 2. At the conclusion of each (full) timestep dt in the Runge-Kutta integration, at time t:

  • (a) For each lymphangion $L_{i}$, if $s_{\mathrm{new}}(i)$ lies in the interval [t - dt, t], initiate contraction of lymphangion $L_{i}$, update $s_{\mathrm{old}}(i)=s_{\mathrm{new}}(i)$, and propagate the signals to nearest-neighbour lymphangions $L_{i-1}$ and $L_{i+1}$. These lymphangions may then initialize contraction after a delay $t_{\mathrm{p}}$, by updating $s_{\mathrm{new}}(i + 1) = \mathrm{min}(\hbox {s}_{\mathrm{new}}({i}+ 1)$, $t+t_{\mathrm{p}})$ and similarly for $s_{\mathrm{new}}(i - 1)$, but the updates can only occur if they are outside the current relevant refractory period, e.g. for the case of the neighbouring lymphangion $L_{i+1}$, set $s_{\mathrm{new}}(i + 1) = t+t_{\mathrm{p}}$ only if $t+t_{\mathrm{p}} > s_{\mathrm{old}}(i + 1)$ + $t_{\mathrm{n}}$.

  • (b) For each lymphangion $L_{i}$, if the time of conclusion of a contraction lies in the interval [$t - dt, t$], update $s_{\mathrm{new}}(i) = \hbox {min}(s_{\mathrm{old}}(i)+ t_{\mathrm{n}}$, $t+t_{\mathrm{r}})$, where $t_{\mathrm{r}}$ is calculated according to the average of $\Delta p_{\mathrm{tm}}(t)$ over the just-concluded contraction.