Sparse Kalman filtering approaches to realized covariance estimation from high frequency financial data

Abstract

Estimation of the covariance matrix of asset returns from high frequency data is complicated by asynchronous returns, market microstructure noise and jumps. One technique for addressing both asynchronous returns and market microstructure is the Kalman-Expectation-Maximization (KEM) algorithm. However the KEM approach assumes log-normal prices and does not address jumps in the return process which can corrupt estimation of the covariance matrix. In this paper we extend the KEM algorithm to price models that include jumps. We propose a sparse Kalman filtering approach to this problem. In particular we develop a Kalman Expectation Conditional Maximization algorithm to determine the unknown covariance as well as detecting the jumps. In order to promote a sparse estimate of the jumps,we consider both Laplace and the spike and slab jump priors. Numerical results using simulated data show that each of these approaches provide for improved covariance estimation relative to the KEM method in a variety of settings where jumps occur.

Appendices

Appendices

A Kalman smoothing equations

The Kalman smoother can be used to compute the posterior distribution of X(t) given Y and an estimate of $\varTheta = [D,\varGamma ,\varSigma _{o}',J]$. From [35] the posterior distribution is normal and is completely characterized by the following quantities for $m=T$

$$\begin{aligned} \bar{X}(t|m)= & {} \mathbb {E}(X(t)|y(1:m))\\ P(t|m)= & {} cov (X(t),X(t)|y(1:m))\\ P(t,t-1|m)= & {} cov (X(t),X(t-1)|y(1:m)). \end{aligned}$$

These values can be computed efficiently using a set of well known forward and backward recursions [34] known as the Rauch–Tung–Striebel (RTS) smoother. The forward recursions are

$$\begin{aligned} \bar{X}(t|t-1)= & {} \bar{X}(t-1|t-1)+D+J(t) \end{aligned}$$

(24)

$$\begin{aligned} P(t|t-1)= & {} P(t-1|t-1)+\varGamma \end{aligned}$$

(25)

$$\begin{aligned} G(t)= & {} P(t|t-1)I(t)^{T}\left( I(t)P(t|t-1)I(t)^{T} + \varSigma _{o}^{2}(t)\right) ^{-1} \end{aligned}$$

(26)

$$\begin{aligned} \bar{X}(t|t)= & {} \bar{X}(t|t-1) +G(t)(y(t)-I(t)\bar{X}(t|t-1)) \end{aligned}$$

(27)

$$\begin{aligned} P(t|t)= & {} P(t|t-1) - G(t)I(t)P(t|t-1) \end{aligned}$$

(28)

with $\bar{X}(0|0)=\mu$ and $P(0|0)=K$.

The backward equations are given by

$$\begin{aligned} H(t-1)= & {} P(t-1|t-1)P(t|t-1)^{-1} \\ \bar{X}(t-1|T)= & {} \bar{X}(t-1|t-1) + H(t-1)(\bar{X}(t|T)-\bar{X}(t|t-1)) \\ P(t-1|T)= & {} P(t-1|t-1) \\&+ H(t-1)(P(t|T)-P(t|t-1))H(t-1)^{T}. \end{aligned}$$

A backward recursion for computing $P(t,t-1|T)$ is

$$\begin{aligned} P(t-1,t-2|T)= & {} P(t-1|t-1)H(t-2)^{T} \\&+ H(t-1)\left( P(t,t-1|T)-P(t-1|t-1) \right) H(t-2)^{T} \end{aligned}$$

where

$$\begin{aligned} P(T,T-1|T)=(I -G(T)I(T))P(T-1|T-1). \end{aligned}$$

(29)

B Convergence of KECM algorithms

Convergence of the EM and ECM algorithms in general is considered in [30, 36] respectively. It is shown in [30] that the ECM algorithm converges to stationary point of the log posterior under the following mild regularity conditions

• 1. Any sequence $\varTheta ^{(k)}$ obtained using the ECM algorithm lies in a compact subset of the parameter space, $\varOmega$. For our case we need to restrict the parameter space such that $\sigma _{o}^{2} \ne 0$ and $\varGamma$ is positive definite.

• 2. $\mathcal {G}(\varTheta ,\varTheta ')$ is continuous in both $\varTheta$ and $\varTheta '$.

• 3. The log posterior $L(\varTheta )$ is continuous in $\varOmega$ and differentiable in the interior of $\varOmega$.

1.1 B.1 Algorithm 1

Since the Laplace prior on J is not differentiable condition 3 is not satisfied and the results in [30] are not directly applicable. However the proofs and solution set in [30] can be modified to handle this irregularity.

Before addressing condition 3 we first verify condition 1. We start by examining the sequence of covariance estimates $\varGamma ^{(k)}$.

Lemma 1

Assume a noisy asset price is observed at least one time for each asset for $t>1$ and that $\tilde{I}(t) \ne 0$ for all t. Let $\varGamma ^{(k)}$ be a sequence of solutions obtained with Algorithm 1, where $\varGamma ^{(0)}$ is positive definite. Then sequences $\varGamma ^{(k)}$ and $\frac{1}{s^{(k)}}$ are bounded where $s^{(k)}$ is the minimum eigenvalue of $\varGamma ^{(k)}$. In addition the sequence $\sigma _{o,i}^{2,(k)}$ is bounded below and above by positive values for all i.

Proof

Since $W_{o}$ is positive definite we have from Eq. (9) that $s^{(k)}$ is bounded below by a positive constant which implies $\frac{1}{s^{(k)}}$ is bounded. Similarly by Eq. (10) we have $\sigma _{o,i}^{2,(k)}$ is bounded below by a positive constant. To prove that $\varGamma ^{(k)}$ is bounded we note that the posterior may be written as

$$\begin{aligned} p(\theta |y)= & {} C_{1}p(y|\theta )p(\theta ) \\= & {} C_{1}p(y(1)|\theta )p(\theta )\prod _{t=2}^{T}p(y(t)|y(1:t-1),\theta )\\\le & {} C_{2} p(y(1)|\theta )\prod _{t=2}^{T}p(y(t)|y(1:t-1),\theta ) \end{aligned}$$

where $C_{1}$ is a constant not dependent on $\theta$ and where $C_{2} = C_{1}\sup _{\theta }p(\theta )$. Note that $C_{2} < \infty$.

For $t>1$ each of the conditional distributions $p(y(t)|y(1:t-1),\theta )$ is a normal distribution with covariance

$$\begin{aligned} Q(t)=\tilde{I}(t)P(t|t-1)\tilde{I}(t)^{T}+\sigma _{o}^{2}I \end{aligned}$$

where for notational simplicity we suppress the dependence of Q(t) and $P(t|t-1)$ on k. Since $\sigma _{o,i}^{2}$ is bounded below by a positive value, it follows that $\frac{1}{|Q(t)|}$ is bounded.

Now suppose that $\varGamma ^{(k)}$ is unbounded. Then since

$$\begin{aligned} P(t|t-1) = P(t-1|t-1)+\varGamma \end{aligned}$$

$P(t|t-1)$ is unbounded as k goes to $\infty$. Since an observation of each asset’s price occurs at least once for $t>1$ it follows that $Q(\tau )$ is unbounded (as $k \rightarrow \infty$) for some $\tau >1$. Then since the smallest eigenvalue of $Q(\tau )$ is bounded below by a positive constant, the determinant of $Q(\tau )$ is unbounded. Thus a subsequence of $p(y(\tau )|y(1:\tau -1),\varTheta ^{(k)})$ will approach 0. Since $\frac{1}{|Q(t)|}$ is bounded, $p(y(t)|y(1:t-1),\varTheta ^{(k)})$ will remain bounded above for all t. Then using (30) we have

$$\begin{aligned} p(\theta |y)\le & {} C_{2} p(y(1)|\theta )\prod _{t=2}^{T}p(y(t)|y(1:t-1),\theta ) \\= & {} C_{2} p(y(\tau )|y(1:\tau -1),\theta )\prod _{t\ne \tau }^{T}p(y(t)|y(1:t-1),\theta ) \end{aligned}$$

which implies a subsequence of $p(\varTheta ^{(k)}|y)$ will converge to 0. This contradicts the monotonicity of the ECM algorithm [30]. The proof that the sequence $\sigma _{o,i}^{2,(k)}$ is bounded above for all i is similar. $\square$

Lemma 2

Assume the conditions of Lemma 1. Let $\lambda (t)^{-1,(k)}$ be a sequence of solutions obtained with Algorithm 1 where $\varGamma ^{(0)}$ is positive definite. Then there exist finite positive numbers a, b where $a\le \lambda _{i}(t)^{(k)} \le b$ for all t, k and i.

Proof

By the update equation (14) we may set $b=\frac{\alpha _{\lambda }+2}{\beta _{\lambda }}$ which is positive and finite. By way of contradiction assume the lower bound does not hold. Then for some i and t there exists a subsequence $\lambda _{i}(t)^{(k_{n})}$ such that $\lim _{n \rightarrow \infty } \lambda _{i}(t)^{-1,(k_{n})} =\infty$. Since each $\lambda _{i}(t)^{-1}$ is the mode of an inverse gamma distribution it follows that the posterior scale parameter,($\beta _{\lambda }+|j^{(k_{n})}|$) goes to infinity . This implies that $p(\lambda _{i}(t)^{-1,(k_{n})},j_{i}(t)^{(k_{n})}) \rightarrow 0$. Since each prior density function is bounded as $\lambda _{i}(t) \rightarrow 0$ this implies that $p(\theta )$ goes to zero, contradicting the monotonicity of the ECM algorithm. Thus there exists an $a>0$ such that $\lambda _{i}(t)^{(k)}>a$ for all t, k and i. $\square$

Now we prove that the sequences $J^{(k)}$ and $D^{(k)}$ are also well behaved.

Lemma 3

Assume the conditions of Lemma 1. Let $J^{(k)}$ and $D^{(k)}$ be sequences of solutions obtained with Algorithm 1 where $\varGamma ^{(0)}$ is positive definite. Then sequences $J^{(k)}$ and $D^{(k)}$ are bounded.

Proof

From Lemma 1 the likelihood $p(y|\theta )$ is bounded above. Recall from the previous lemma that there exists an $a>0$ such that for all k, $\lambda _{i}(t)^{(k)} \ge a$. Since the prior density function is bounded above for each parameter it follows that $\lim _{j \rightarrow \infty } p(\theta ) =0$. This implies $J^{(k)}$ is bounded by the monotonicity of the ECM algorithm. Since $\lim _{d \rightarrow \infty } p(\theta ) =0$ it also follows that $D^{(k)}$ is bounded. $\square$

The above lemmas imply the following corollary.

Corollary 1

The sequence $\varTheta ^{(k)}$ is bounded and all limit points are feasible ( e.g. variance non-zero, positive definite covariance).

Now we derive some additional properties of the limit points of $\varTheta ^{(k)}$. To do this we shall refer to Zangwill’s convergence theorem [37]. To use Zangwill’s theorem, we first define $\mathcal {A}$ to be a point to set mapping defined by the ECM algorithm i.e. $\varTheta ^{(k+1)} \in \mathcal {A}(\varTheta ^{(k)})$. Let us define a solution set, $\mathcal {S}$, as the set of $\theta$ such that

$$\begin{aligned} \theta _{1}= & {} \arg \max _{v} \mathcal {G}\left( \left[ v,\theta _{2},\theta _{3},\theta _{4},\theta _{5} \right] ,\theta \right) \\ \theta _{2}= & {} \arg \max _{v} \mathcal {G}\left( \left[ \theta _{1},v,\theta _{3},\theta _{4},\theta _{5} \right] ,\theta \right) \\ \theta _{3}= & {} \arg \max _{v} \mathcal {G}\left( \left[ \theta _{1},\theta _{2},v,\theta _{4},\theta _{5} \right] ,\theta \right) \\ \theta _{4}= & {} \arg \max _{v} \mathcal {G}\left( \left[ \theta _{1},\theta _{2},\theta _{3},v,\theta _{5} \right] ,\theta \right) \\ \theta _{5}= & {} \arg \max _{v} \mathcal {G}\left( \left[ \theta _{1},\theta _{2},\theta _{3},\theta _{4},v \right] ,\theta \right) . \end{aligned}$$

By definition $\theta \in \mathcal {A}(\theta )$ for all $\theta \in \mathcal {S}$. This along with the monotonicity of the ECM algorithm implies that $L(\theta )$ is an ascent function, i.e.

$$\begin{aligned} L(\theta ')> L(\theta ) \quad \text{ for } \text{ all } \theta \not \in \mathcal {S}, \theta ' \in \mathcal {A}(\theta )\\ L(\theta ')\ge L(\theta ) \quad \text{ for } \text{ all } \theta \in \mathcal {S}, \theta ' \in \mathcal {A}(\theta ). \end{aligned}$$

Since $\mathcal {G}(\theta ,\theta ')$ is continuous in both $\theta$ and $\theta '$ we have that $\mathcal {A}$ is a closed mapping. Thus we have the following theorem.

Theorem 1

All limit points of $\varTheta ^{(k)}$ belong to $\mathcal {S}$.

Proof

This is a direct consequence of Zangwill’s convergence theorem [37] (also known as the Global convergence theorem [27]). To invoke the theorem we must meet the following conditions

• $\varTheta ^{(k)}$ belongs to a compact subset of the feasible solutions

• $\mathcal {A}$ is closed

• There exists a continuous ascent function

All three of these conditions were shown above, thus the theorem follows from Zangwill’s convergence theorem. $\square$

Now we show that if $\theta ' \in \mathcal {S}$ then $\theta '$ is in some sense a “stationary” point of the log posterior $L(\theta )=\log p(\theta |y)$.

Theorem 2

Let $\theta ' \in \mathcal {S}$. Then

$$\begin{aligned} \nabla _{\theta _{i}} L(\theta )_{|\theta =\theta '} =0 \quad \text{ for } i \in {1,2,3,5} \end{aligned}$$

and

$$\begin{aligned} 0 \in \partial _{\theta _{4}} L(\theta )_{|\theta =\theta '}. \end{aligned}$$

Proof

To show this we first note that $L(\theta )$ can be written as [30]

$$\begin{aligned} L(\theta |y) = \mathcal {G}(\theta ,\theta ') - H(\theta ,\theta ') \end{aligned}$$

where

$$\begin{aligned} H(\theta ,\theta ') = \mathbb {E}_{p(x|y,\theta ')}\log p(X|y,\theta ). \end{aligned}$$

From the information inequality we have that $H(\theta ',\theta ') \ge H(\theta ,\theta ')$ for all feasible $\theta$. Since $H(\theta ,\theta ')$ is differentiable with respect to $\theta$ it follows that

$$\begin{aligned} \nabla _{\theta } H(\theta ,\theta ')_{|\theta =\theta '} = 0. \end{aligned}$$

Since $\nabla _{\theta _{i}}\mathcal {G}(\theta ,\theta ')_{|\theta =\theta '}=0$ for $i \in {1,2,3,5}$ it follows that

$$\begin{aligned} \nabla _{\theta _{i}} L(\theta )_{|\theta =\theta '} =0 \quad \text{ for } i \in {1,2,3} \end{aligned}$$

Also since $\mathcal {G}(\theta ,\theta ')$ and $H(\theta ,\theta ')$ are convex in j, and $\theta ' \in \mathcal {S}$, it follows that

$$\begin{aligned} 0 \in \partial _{\theta _{4}} \mathcal {G}(\theta ,\theta ') \end{aligned}$$

which implies

$$\begin{aligned} 0 \in \partial _{\theta _{4}} L(\theta ,\theta '). \end{aligned}$$

$\square$

1.2 B.2 Algorithm 3

Analogous results to Corollary 1 and Theorem 1 may proven for Algorithm 3 using same arguments as Algorithm 1. The following result is analogous to Theorem 2.

Theorem 3

Let $\theta ' \in \mathcal {S}$ where $\mathcal {S}$ is the set of fixed points of the Algorithm 3. Then

$$\begin{aligned} \nabla _{\theta _{i}} L(\theta )_{|\theta =\theta '} =0\quad \text{ for } i \in {1,2,3,5,6}. \end{aligned}$$

The proof of this result is the same as Theorem 2.

C Procedure for selecting $q(\lambda )$

In this section we outline the method for selecting the distribution $q(\lambda )$ for a special case of when the prior distribution of volatility of each asset is identical. Suppose the squared volatility of each asset return is inverse gamma distributed with scale c and shape $\eta$. Let $\sigma _{v}^{2}$ be distributed as $IG(c,\eta )$ and be statistically independent of $\zeta '$ and $\sigma _{j}^{2}$.

To determine an appropriate prior distribution of $\lambda$ we first obtain samples of $\lambda$,

$$\begin{aligned} \tilde{\lambda }_{1}, \dots , \tilde{\lambda }_{M_{\lambda }} \end{aligned}$$

by the performing the following steps

• 1. For $k=1, \dots , M_{\lambda }$

• 2. Draw independent samples from the distribution of $(\sigma _{v}^{2'},\zeta ',\sigma _{j}^{2'})$. This is relatively straight forward using standard statistical functions due to the independence assumptions.

• 3. Determine a $\lambda '$ such that $\lambda ' \sim _{\sigma _{v}^{2'}} (\zeta ',\sigma _{j}^{2'})$. This can be done via Monte Carlo integration as shown below.

  • For a large number L draw a sample $v_{1} \dots v_{L}$ from the distribution $\mathcal {N}(0,\sigma _{v}^{2})$.

  • Compute $P_{i}=Pr(J=0|J+V=v_{i})$, where $J \sim SpikeSlab(\zeta ',\sigma _{j}^{2'})$. The value of $P_{i}$ is

    $$\begin{aligned} \frac{ \frac{\zeta '}{\sqrt{\sigma _{v}^{2'}}}\exp (-v_{i}^{2}/(2\sigma _{v}^{2})) }{\frac{\zeta '}{\sqrt{\sigma _{v}^{2'}}}\exp (-v_{i}^{2}/(2\sigma _{v}^{2'})) + \frac{1-\zeta '}{\sqrt{\sigma _{v}^{2'}+\sigma _{j}^{2'}}}\exp (-v_{i}^{2}/(2( \sigma _{v}^{2'}+\sigma _{j}^{2'})))}. \end{aligned}$$

  • Compute the simulated empirical mean $\bar{P}=\frac{1}{L}\sum _{i=1}^{L} P_{i}$.

  • Choose $\lambda '$ such that (5) is satisfied with $\mathbb {E}_{p(y_{2}|J_{2}=0)}Pr(J_{2}=0|Y_{2})$ approximated as $\bar{P}$. This value is given below

    $$\begin{aligned} \lambda ' =\frac{\text{ erf }^{-1}(\bar{P})\sqrt{2\sigma _{v}^{2'}}}{\sigma _{v}^{2'}} \end{aligned}$$

    where $\text{ erf }^{-1}()$ is the inverse error function.

• 4. Set $\tilde{\lambda }_{k}=\lambda '$

• 5. Goto step 1

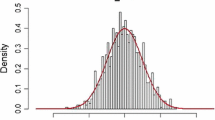
Examples of histograms of samples obtained using the above procedures are shown in Fig. 5. Once we obtain samples of $\lambda$ we fit a smooth distribution to the sampled data. Since the gamma distribution is a conjugate prior to the Laplace distribution a gamma distribution is a convenient choice for $q(\lambda )$. Furthermore examination of Fig. 5 indicates that a gamma distribution is a reasonable approximation. Thus we choose

$$\begin{aligned} q(\lambda ) = \frac{\beta _{\lambda }^{\alpha _{\lambda }}}{\varGamma _{f}(\alpha _{\lambda })} \lambda ^{\alpha _{\lambda }-1}\exp \left( -\lambda \beta _{\lambda }\right) \end{aligned}$$

where $\varGamma _{f}()$ is the gamma function. Here $\alpha _{\lambda }$ and $\beta _{\lambda }$ can be selected using maximum likelihood or method of moments.

Since $q(\lambda )$ develops a singularity near zero for large values of $\beta _{\lambda }$ we shall impose a prior of $\lambda ^{-1}$ rather than $\lambda$. We denote this prior as $q_{inv}(\lambda ^{-1})$. Since $\lambda$ is gamma distributed with shape $\alpha _{\lambda }$ and rate $\beta _{\lambda }$ it follows that $q_{inv}(\lambda ^{-1})$ is the inverse gamma distribution with shape $\alpha _{\lambda }$ and scale $\beta _{\lambda }$

$$\begin{aligned} q_{inv}(\lambda ^{-1})=\frac{\beta _{\lambda }^{\alpha _{\lambda }}}{\varGamma _{f} (\alpha _{\lambda })}(\lambda ^{-1})^{-\alpha _{\lambda }-1}\exp \left( -\frac{\beta _{\lambda }}{\lambda ^{-1}}\right) . \end{aligned}$$

Fig. 5

Normalized histograms of $\lambda$ samples. In all experiments $\sigma _{j}^{2} \sim IG(10,0.0011)$, $\zeta \sim \text{ Beta }(5,1.0201)$, $\sigma _{v}^{2} \sim IG(5,\beta _{v})$