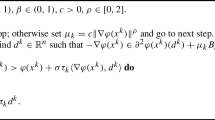Abstract
We consider a class of nonconvex nonsmooth optimization problems whose objective is the sum of a smooth function and a finite number of nonnegative proper closed possibly nonsmooth functions (whose proximal mappings are easy to compute), some of which are further composed with linear maps. This kind of problems arises naturally in various applications when different regularizers are introduced for inducing simultaneous structures in the solutions. Solving these problems, however, can be challenging because of the coupled nonsmooth functions: the corresponding proximal mapping can be hard to compute so that standard first-order methods such as the proximal gradient algorithm cannot be applied efficiently. In this paper, we propose a successive difference-of-convex approximation method for solving this kind of problems. In this algorithm, we approximate the nonsmooth functions by their Moreau envelopes in each iteration. Making use of the simple observation that Moreau envelopes of nonnegative proper closed functions are continuous difference-of-convex functions, we can then approximately minimize the approximation function by first-order methods with suitable majorization techniques. These first-order methods can be implemented efficiently thanks to the fact that the proximal mapping of each nonsmooth function is easy to compute. Under suitable assumptions, we prove that the sequence generated by our method is bounded and any accumulation point is a stationary point of the objective. We also discuss how our method can be applied to concrete applications such as nonconvex fused regularized optimization problems and simultaneously structured matrix optimization problems, and illustrate the performance numerically for these two specific applications.


Similar content being viewed by others
Notes
These follow from (i) and [25, Corollary 8.10].
These follow from (i) and [25, Corollary 8.10].
To see this, recall from [15, Proposition 3.1] that an element \({\varvec{\zeta }}^*\) of \(\mathbf{proj}_{{\varOmega }}({\varvec{y}})\) can be obtained as
$$\begin{aligned} \zeta ^*_i = {\left\{ \begin{array}{ll} {\tilde{\zeta }}^*_i &{} \mathrm{if}\ i \in I^*,\\ 0 &{} \mathrm{otherwise}, \end{array}\right. } \end{aligned}$$where \({\tilde{\zeta }}^*_i = {\hbox {argmin}}\{\frac{1}{2}(\zeta _i - y_i)^2:\; 0\le \zeta _i\le \tau \} = \max \{\min \{y_i,\tau \},0\}\), and \(I^*\) is an index set of size k corresponding to the k largest values of \(\{\frac{1}{2} y_i^2 - \frac{1}{2}({\tilde{\zeta }}^*_i - y_i)^2\}_{i=1}^n = \{\frac{1}{2} y_i^2 - \frac{1}{2}(\min \{\max \{y_i - \tau ,0\},y_i\})^2\}_{i=1}^n\). Since the function \(t\mapsto \frac{1}{2}t^2 - \frac{1}{2}(\min \{\max \{t - \tau ,0\},t\})^2\) is nondecreasing, we can let \(I^*\) correspond to any k largest entries of \({\varvec{y}}\).
To see this, recall from [16, Corollary 2.3] and [15, Proposition 3.1] that an element \({\varvec{Y}} \in \mathbf{proj}_{{\tilde{{\varXi }}}_k}({\varvec{W}})\) can be computed as \({\varvec{Y}} = {\varvec{U}} \mathrm {Diag}({\varvec{\zeta }}^*){\varvec{V}}^\top \), where
$$\begin{aligned} \zeta ^*_i = {\left\{ \begin{array}{ll} {\tilde{\zeta }}^*_i &{} \mathrm{if}\ i \in I^*,\\ 0 &{} \mathrm{otherwise}, \end{array}\right. } \end{aligned}$$where \({\tilde{\zeta }}^*_i = {\hbox {argmin}}\{\frac{1}{2}(\zeta _i - \sigma _i)^2:\; |\zeta _i|\le \tau \} = \min \{\sigma _i,\tau \}\), and \(I^*\) is an index set of size k corresponding to the k largest values of \(\{\frac{1}{2}\sigma _i^2 - \frac{1}{2}({\tilde{\zeta }}^*_i - \sigma _i)^2\}_{i=1}^n = \{\frac{1}{2}\sigma _i^2 - \frac{1}{2}(\max \{0,\sigma _i - \tau \})^2\}_{i=1}^n\). Since \(t\mapsto \frac{1}{2}t^2 - \frac{1}{2}(\max \{0,t - \tau \})^2\) is nondecreasing for nonnegative t, we can take \(I^*\) to correspond to any k largest singular values.
To see this, recall from [16, Proposition 2.8] and [15, Proposition 3.1] that an element \({\varvec{Y}} \in \mathbf{proj}_{{\tilde{{\varPi }}}_k}({\varvec{W}})\) can be computed as \({\varvec{Y}} = {\varvec{U}} \mathrm {Diag}({\varvec{\zeta }}^*){\varvec{V}}^\top \), where
$$\begin{aligned} \zeta ^*_i = {\left\{ \begin{array}{ll} {\tilde{\zeta }}^*_i &{} \mathrm{if}\ i \in I^*,\\ 0 &{} \mathrm{otherwise}, \end{array}\right. } \end{aligned}$$where \({\tilde{\zeta }}^*_i = {\hbox {argmin}}\{\frac{1}{2}(\zeta _i - \lambda _i)^2:\; 0\le \zeta _i\le \tau \} = \max \{\min \{\lambda _i,\tau \},0\}\), and \(I^*\) is an index set of size k corresponding to the k largest values of \(\{\frac{1}{2}\lambda _i^2 - \frac{1}{2}({\tilde{\zeta }}^*_i - \lambda _i)^2\}_{i=1}^n = \{\frac{1}{2}\lambda _i^2 - \frac{1}{2}(\min \{\max \{\lambda _i - \tau ,0\},\lambda _i\})^2\}_{i=1}^n\). Since the function \(t\mapsto \frac{1}{2}t^2 - \frac{1}{2}(\min \{\max \{t - \tau ,0\},t\})^2\) is nondecreasing, we can let \(I^*\) correspond to any k largest entries of \({\varvec{\lambda }}\).
This refers to the total number of inner iterations.
This refers to the total number of inner iterations.
References
Ahn, M., Pang, J.S., Xin, J.: Difference-of-convex learning: directional stationarity, optimality, and sparsity. SIAM J. Optim. 27, 1637–1665 (2017)
Asplund, E.: Differentiability of the metric projection in finite dimensional Euclidean space. Proc. Am. Math. Soc. 38, 218–219 (1973)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, Berlin (2011)
Becker, S., Candès, E.J., Grant, M.: Templates for convex cone problems with applications to sparse signal recovery. Math. Progr. Comput. 3, 165–218 (2011)
Borsdorf, R., Higham, N.J., Raydan, M.: Computing a nearest correlation matrix with factor structure. SIAM J. Matrix Anal. Appl. 31, 2603–2622 (2010)
Brodie, J., Daubechies, I., De Mol, C., Giannone, D., Loris, I.: Sparse and stable Markowitz portfolios. Proc. Natl. Acad. Sci. 106, 12267–12272 (2009)
Candès, E.J., Recht, B.: Exact matrix completion via convex optimization. Found. Comput. Math. 9, 717–772 (2009)
Chen, C., Li, X., Tolman, C., Wang, S., Ye, Y.: Sparse portfolio selection via quasi-norm regularization. arXiv:1312.6350, (2013)
Eckstein, J., Bertsekas, D.P.: On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Progr. 55, 293–318 (1992)
Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximations. Comput. Math. Appl. 2, 17–40 (1976)
Gao, Y., Sun, D.: A majorized penalty approach for calibrating rank constrained correlation matrix problems, Technical report, National University of Singapore (2010)
Gong, P., Zhang, C., Lu, Z., Huang, J., Ye, J.: A general iterative shrinkage and thresholding algorithm for non-convex regularized optimization problems. In: Proceedings of the 30th International Conference on Machine Learning, 37–45 (2013)
Li, G., Pong, T.K.: Global convergence of splitting methods for nonconvex composite optimization. SIAM J. Optim. 25, 2434–2460 (2015)
Lu, Z., Li, X.: Sparse recovery via partial regularization: models, theory and algorithms. arXiv:1511.07293 (2015)
Lu, Z., Zhang, Y.: Sparse approximation via penalty decomposition methods. SIAM J. Optim. 23, 2448–2478 (2013)
Lu, Z., Zhang, Y., Li, X.: Penalty decomposition methods for rank minimization. Optim. Methods Softw. 30, 531–558 (2015)
Lucet, Y.: Fast Moreau envelope computation I: numerical algorithms. Numer. Algorithms 43, 235–249 (2006)
Markovsky, I.: Structured low-rank approximation and its applications. Automatica 44, 891–909 (2008)
Markowitz, H.: Portfolio selection. J. Financ. 7, 77–91 (1952)
Nesterov, Y.: Smooth minimization of non-smooth functions. Math. Progr. 103, 127–152 (2005)
Parekh, A., Selesnick, I.W.: Convex fused Lasso denoising with non-convex regularization and its use for pulse detection. In: Proceedings of IEEE Signal Processing in Medicine and Biology Symposium, 1–6 (2015)
Recht, B., Fazel, M., Parrilo, P.A.: Guaranteed minimum-rank solutions for linear matrix equations via nuclear norm minimization. SIAM Rev 52, 471–501 (2010)
Richard, E., Savalle, P.-A., Vayatis, N.: Estimation of simultaneously sparse and low rank matrices. arXiv:1206.6474 (2012)
Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton (1970)
Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis. Springer, Berlin (1998)
Slawski, M., Hein, M.: Non-negative least squares for high-dimensional linear models: consistency and sparse recovery without regularization. Electron. J. Stat. 7, 3004–3056 (2013)
Thiao, M., Pham, D.T., Le Thi, H.A.: A DC programming approach for sparse eigenvalue problem. In: Proceedings of the 27th International Conference on Machine Learning, 1063–1070 (2010)
Tibshirani, R.: Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B 58, 267–288 (1996)
Tibshirani, R., Taylor, J.: The solution path of the generalized Lasso. Ann. Stat. 39, 1335–1371 (2011)
Tono, K., Takeda, A., Gotoh, J.: Efficient DC algorithm for constrained sparse optimization. arXiv:1701.08498 (2017)
Wright, S.J., Nowak, R.D., Figueiredo, M.A.T.: Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 57, 2479–2493 (2009)
Yu, Y.L.: Better approximation and faster algorithm using the proximal average. Adv. Neural Inf. Process. Syst. 26, 458–466 (2013)
Yu, Y.L., Zheng, X., Marchetti-Bowick, M., Xing, E.: Minimizing nonconvex non-separable functions. In: Proceedings of the 18th International Conference on Artificial Intelligence and Statistics 38, 1107–1115 (2015)
Author information
Authors and Affiliations
Corresponding author
Additional information
Ting Kei Pong is supported in part by Hong Kong Research Grants Council PolyU153085/16p. Akiko Takeda is supported by Grant-in-Aid for Scientific Research (C), 15K00031.
A Convergence of an NPG method with majorization
A Convergence of an NPG method with majorization
In this appendix, we consider the following optimization problem:
where h is an \(L_h\)-smooth function, P is a proper closed function with \(\inf P > -\infty \) and g is a continuous convex function. We assume in addition that there exists \({\varvec{x}}^0\in \mathrm{dom}\,P\) so that F is continuous in \({\varOmega }({\varvec{x}}^0):= \{{\varvec{x}}:\; F({\varvec{x}})\le F({\varvec{x}}^0)\}\) and the set \({\varOmega }({\varvec{x}}^0)\) is compact. As a consequence, it holds that \(\inf F > -\infty \).
In Algorithm 2 below, we describe an algorithm, the nonmonotone proximal gradient method with majorization (\(\hbox {NPG}_{\mathrm{major}}\)), for solving (44). We first show that the line-search criterion is well-defined.

Proposition 1
For each t, the condition (46) is satisfied after at most
inner iterations, which is independent of t. Consequently, \(\{{\bar{L}}_t\}\) is bounded.
Proof
For each t and \(L > 0\), let \({\varvec{u}}^t_L\) be an arbitrarily fixed element in
Then we have
where the first inequality holds because of the \(L_h\)-smoothness of h, the convexity of g and the fact that \({\varvec{\zeta }}^t\in \partial g({\varvec{x}}^t)\), and the last inequality follows from the definition of \({\varvec{u}}^t_L\) as a minimizer. Thus, at the t-th iteration, the criterion (46) is satisfied by \({\varvec{u}} = {\varvec{u}}^t_L\) whenever \(L \ge L_h + c\). Since we have
we conclude that (46) must be satisfied at or before the \({\tilde{n}}\)-th inner iteration. Consequently, we have \({\bar{L}}_t \le \tau ^{{\tilde{n}}}L_{\max }\) for all t. \(\square \)
The convergence of \(\hbox {NPG}_{\mathrm{major}}\) can now be proved similarly as in [31, Lemma 4].
Proposition 2
Let \(\{{\varvec{x}}^t\}\) be the sequence generated by \(\hbox {NPG}_{\mathrm{major}}\). Then \(\Vert {\varvec{x}}^{t+1} - {\varvec{x}}^t\Vert \rightarrow 0\).
Rights and permissions
About this article
Cite this article
Liu, T., Pong, T.K. & Takeda, A. A successive difference-of-convex approximation method for a class of nonconvex nonsmooth optimization problems. Math. Program. 176, 339–367 (2019). https://doi.org/10.1007/s10107-018-1327-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-018-1327-8