Distributionally robust shortfall risk optimization model and its approximation

Abstract

Utility-based shortfall risk measures (SR) have received increasing attention over the past few years for their potential to quantify the risk of large tail losses more effectively than conditional value at risk. In this paper, we consider a distributionally robust version of the shortfall risk measure (DRSR) where the true probability distribution is unknown and the worst distribution from an ambiguity set of distributions is used to calculate the SR. We start by showing that the DRSR is a convex risk measure and under some special circumstance a coherent risk measure. We then move on to study an optimization problem with the objective of minimizing the DRSR of a random function and investigate numerical tractability of the optimization problem with the ambiguity set being constructed through $\phi$-divergence ball and Kantorovich ball. In the case when the nominal distribution in the balls is an empirical distribution constructed through iid samples, we quantify convergence of the ambiguity sets to the true probability distribution as the sample size increases under the Kantorovich metric and consequently the optimal values of the corresponding DRSR problems. Specifically, we show that the error of the optimal value is linearly bounded by the error of each of the approximate ambiguity sets and subsequently derive a confidence interval of the optimal value under each of the approximation schemes. Some preliminary numerical test results are reported for the proposed modeling and computational schemes.

1 Introduction

Quantitative measure of risk is a key element for financial institutions and regulatory authorities. It provides a way to compare different financial positions. A financial position can be mathematically characterized by a random variable $Z: (\varOmega ,\mathscr {F},P) \rightarrow \mathrm{I\!R}$, where $\varOmega$ is a sample space with sigma algebra $\mathscr {F}$ and P is a probability measure. A risk measure $\rho$ assigns to Z a number that signifies the risk of the position. A good risk measure should have some virtues, such as being sensitive to excessive losses, penalizing concentration and encouraging diversification, and supporting dynamically consistent risk managements over multiple horizons [15].

Artzner et al. [1] considered the axiomatic characterizations of risk measures and first introduced the concept of coherent risk measure, which satisfies: (a) positive homogeneity ($\rho (\alpha Z)=\alpha \rho (Z)$ for $\alpha \ge 0$); (b) subadditivity ($\rho (Z+Y) \le \rho (Z)+ \rho (Y)$); (c) monotonicity (if $Z \ge Y$, then $\rho (Z) \le \rho (Y)$); (d) translation invariance (if $m \in \mathrm{I\!R}$, then $\rho (Z+m)=\rho (Z)-m$). Frittelli and Rosazza Gianin [12], Heath [17] and Föllmer and Schied [9] extended the notion of coherent risk measure to convex risk measure by replacing positive homogeneity and subadditivity with convexity, that is, $\rho (\alpha Z+(1-\alpha ) Y) \le \alpha \rho (Z) +(1-\alpha ) \rho (Y)$, for all $\alpha \in [0,1]$. Obviously positive homogeneity and subadditivity imply convexity but not vice versa. In other words, a coherent risk measure is a convex risk measure but conversely it may not be true.

A well-known coherent risk measure is conditional value at risk (CVaR) defined by $\text{ CVaR }_{\alpha }(Z):=\frac{1}{\alpha } \int _0^{\alpha } \text{ VaR }_{\lambda } (Z) d \lambda$, where $\text{ VaR }_{\lambda } (Z)$ denotes the value at risk (VaR) which in this context is the smallest amount of cash that needs to be added to Z such that the probability of the financial position falling into a loss does not exceed a specified level $\lambda$, that is, $\text{ VaR }_{\lambda }(Z):=\inf \{t \in \mathrm{I\!R}: P(Z+t < 0) \le \lambda \}$. In a financial context, CVaR has a number of advantages over the commonly used VaR, and CVaR has been proposed as the primary tool for banking capital regulation in the draft Basel III standard [2]. However, CVaR has a couple of deficiencies.

One is that CVaR is not invariant under randomization, a property which is closely related to the weak dynamic consistency of risk measurements, that is, if $\text{ CVaR }_{\alpha }(Z_i) \le 0$, for $i=1,2$ and $Z:=\left\{ \begin{array}{ll} Z_1, &{}\text{ with } \text{ probability }\,p,\\ Z_2, &{}\text{ with } \text{ probability }\,1-p,\\ \end{array} \right.$ for $p \in (0,1)$, then we do not necessarily have $\text{ CVaR }_{\alpha }(Z)\le 0$, see [26, Example 3.4]. The other is that CVaR is not particularly sensitive to heavy tailed losses [15, Sect. 5]. Here, we illustrate this by a simple example. Let

$$\begin{aligned} X_1:= & {} {\left\{ \begin{array}{ll} 100, &{}p_1= 98\%\\ -100, &{}p_2=1\%\\ -200, &{}p_3=1\% \end{array}\right. },\nonumber \\ X_2:= & {} {\left\{ \begin{array}{ll} 100, &{}p_1= 98\%\\ -1,&{}p_2=1\%\\ -299, &{}p_3=1\% \end{array}\right. },\nonumber \\ X_3:= & {} {\left\{ \begin{array}{ll} 100, &{}p_1= 98\%\\ 99, &{}p_2=1\%\\ -399, &{}p_3=1\% \end{array}\right. }. \end{aligned}$$

(1)

It is easy to calculate that $\text{ CVaR }_{0.02}(X_1)=\text{ CVaR }_{0.02}(X_2)=\text{ CVaR }_{0.02}(X_3)=150$.

To overcome the deficiencies, a special category of convex risk measure, called utility-based shortfall risk measure (abbreviated as SR hereafter) was introduced by Föllmer and Schied [9] and attracted more and more attention in recent years, see [7, 15, 18]. Let $l:\mathrm{I\!R}\rightarrow \mathrm{I\!R}$ be a convex, increasing and non-constant function. Let $\lambda$ be a pre-specified constant in the interior of the range of l to reveal the risk level. The SR of a financial position Z is defined as

$$\begin{aligned} \text{(SR) } \quad \text{ SR }_{l,\lambda }^{P}(Z):=\inf \{t\in \mathrm{I\!R}:t+Z \in {\mathcal {A}}_P\}, \end{aligned}$$

(2)

where ${\mathcal {A}}_P:=\{Z \in L^{\infty }:{\mathbb {E}}_P[l(-Z(\omega ))]\le \lambda \}$ is called the acceptance set and $L^{\infty }$ denotes the set of bounded random variables. From the definition, we can see that the SR is the smallest amount of cash that must be added to the position Z to make it acceptable, i.e., $t+Z \in {\mathcal {A}}_P$. Observe that when $l(\cdot )$ takes a particular characteristic function of the form $\mathbb {1}_{(0,+\infty )}(\cdot )$, that is $\mathbb {1}_{(0,+\infty )}(z)=1$ if $z \in (0,+\infty )$, and 0 otherwise, in such a case $\text{ SR }_{l,\lambda }^{P}(Z)$ coincides with $\text{ VaR }_{\lambda }(Z)$. Of course, here l is nonconvex.

Compared to CVaR, SR not only satisfies convexity, but also satisfies invariance under randomization and can be used more appropriately for dynamic measurement of risks over time. To see invariance under randomization, we note that SR defined as in (2) is a function on the space of random variables, it can also be represented as a function on the space of probability measures, see [26, Remark 2.1]. In the latter case, the acceptance set can be characterized by ${\mathcal {N}}:=\{\mu \in \mathscr {P}(C): \int _C l(-x) \mu (d x)\le \lambda \}$, where $\mathscr {P}(C)$ denotes the space of probability measures with support being contained in a compact set $C \subset \mathrm{I\!R}$. If $\mu , \nu \in {\mathcal {N}}$, i.e., $\int _C l(-x) \mu (d x)\le \lambda , \int _C l(-x) \nu (d x)\le \lambda$, then for any $\alpha \in (0,1)$, $\int _C l(-x) (\alpha \mu +(1-\alpha )\nu )(d x)\le \lambda$, which means $\alpha \mu +(1-\alpha )\nu \in {\mathcal {N}}$. Moreover, the SR is found to be more sensitive to financial losses from extreme events with heavy tailed distributions, see [15, Sect. 5]. Indeed, if we set $l(z)=e^z$ and $\lambda =e$, then we can easily calculate the shortfall risk values of $X_1,X_2$ and $X_3$ in (1) with $\text{ SR }_{l,\lambda }^P (X_1) \approx 194, \text{ SR }_{l,\lambda }^P(X_2) \approx 293,$ and $\text{ SR }_{l,\lambda }^P(X_3) \approx 393$. Furthermore, if we choose $l(z)=e^{\beta z}$ with $\beta >0$, the resulting SR coincides, up to an additive constant, with the entropic risk measure, that is,

$$\begin{aligned} \text{ SR }_{l,\lambda }^P(Z) =\inf \{t\in \mathrm{I\!R}: {\mathbb {E}}_P[e^{-\beta (Z+t)}] \le \lambda \} =\frac{1}{\beta } \left( \log {\mathbb {E}}_P[e^{-\beta Z}]-\log \lambda \right) . \end{aligned}$$

In the case when $l(z)=z^{\alpha } \mathbb {1}_{[0,+\infty )}(z)$ with $\alpha \ge 1$, the associated risk measure focuses on downside risk only and thus neglects the tradeoff between gains and losses.

Dunkel and Weber [7] are perhaps the first to discuss the computational aspects of SR. They characterized SR as a stochastic root finding problem and proposed the stochastic approximation (SA) method combined with importance sampling techniques to calculate it. Hu and Zhang [18] proposed an alternative approach by reformulating SR as the optimal value of a stochastic optimization problem and applying the well-known sample average approximation (SAA) method to solve the latter when either the true probability distribution is unknown or it is prohibitively expensive to compute the expected value of the underlying random functions. A detailed asymptotic analysis of the optimal values obtained from solving the sample average approximated problem was also provided.

In some practical applications, however, the true probability distribution may be unknown and it is expensive to collect a large set of samples or the samples are not trustworthy. However, it might be possible to use some partial information such as empirical data, computer simulation, prior moments or subjective judgements to construct a set of distributions which contains or approximates the true probability distribution in good faith. Under these circumstances, it might be reasonable to consider a distributionally robust version of (2) in order to hedge the risk arising from ambiguity of the true probability distribution,

$$\begin{aligned} (\text{ DRSR }) \quad \text{ SR }_{l,\lambda }^{{\mathcal {P}}}(Z):=\inf \{t\in \mathrm{I\!R}:t+Z \in {\mathcal {A}}_{{\mathcal {P}}}\}, \end{aligned}$$

(3)

where ${\mathcal {A}}_{{\mathcal {P}}}:=\{Z \in L^{\infty }: \sup _{P \in {\mathcal {P}}} {\mathbb {E}}_P[l(-Z)]\le \lambda \}$, and ${\mathcal {P}}$ is a set of probability distributions. Föllmer and Schied seem to be the first to consider the notion of distributionally robust SR (DRSR). In [10, Corollary 4.119], they established a robust representation theorem for DRSR. More recently, Wiesemann et al. [27] demonstrated how a DRSR optimization problem may be reformulated as a tractable convex programming problem when l is piecewise affine and the ambiguity set is constructed through some moment conditions, see [27, Example 6] for details.

In this paper, we take on the research by giving a more comprehensive treatment of DRSR. We start by looking into the properties of DRSR and then move on to discuss some optimization problems associated with DRSR. Specifically, for a loss $c(x,\xi )$ associated with decision vector $x\in X \subset \mathrm{I\!R}^n$ and random vector $\xi \in \mathrm{I\!R}^k$, we consider an optimization problem which aims to minimize the distributionally robust shortfall risk measure of the random loss:

$$\begin{aligned} \text{(DRSRP) }\quad \begin{array}{cl} \displaystyle \min _{x \in X}&\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(-c(x,\xi )), \end{array} \end{aligned}$$

(4)

where $\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(\cdot )$ is defined as in (3). We present a detailed discussion on (DRSRP) including tractable reformulation for the problem when the ambiguity set has a specific structure.

As far as we are concerned, the main contribution of the paper can be summarized as follows. First, we demonstrate that DRSR is the worst-case SR (Proposition 1) and hence it is a convex risk measure. Second, we investigate tractability of (DRSRP) by considering particular cases where the ambiguity set ${\mathcal {P}}$ is constructed respectively through $\phi$-divergence ball and Kantorovich ball. Since the structure of ${\mathcal {P}}$ often involves sample data, we analyse convergence of the ambiguity set as the sample size increases (Propositions 3 and 5). To quantify how the errors arising from the ambiguity set propagate to the optimal value of (DRSRP), we then show under some moderate conditions that the error of the optimal value is linearly bounded by the error of the ambiguity set and subsequently derive finite sample guarantee (Theorem 1) and confidence intervals for the optimal value of (DRSRP) associated with the ambiguity sets (Theorem 2 and Corollary 1). Finally, as an application, we apply the (DRSRP) model to a portfolio management problem and carry out various out-of-sample tests on the numerical schemes for the (DRSRP) model with simulated data and real data (Sect. 5).

The rest of the paper is organised as follows. In Sect. 2, we present the properties of DRSR, that is, it is a convex risk measure and it is the worst-case SR. In Sect. 3, we derive the formulation of (DRSRP) when the ambiguity set is constructed through $\phi$-divergence ball and Kantorovich ball and then establish the convergence of ambiguity sets as sample size increases. In Sect. 4, the finite sample guarantees on the quality of the optimal solutions and convergence of the optimal values as the sample size increases are discussed. In Sect. 5, we report results of numerical experiments.

Throughout the paper, we use $\mathrm{I\!R}^n$ to represent n dimensional Euclidean space and $\mathrm{I\!R}^n_+$ nonnegative orthant. Given a norm $\Vert \cdot \Vert$ in $\mathrm{I\!R}^n$, the dual norm $\Vert \cdot \Vert _{*}$ is defined by $\Vert y\Vert _{*}:=\sup _{\Vert z\Vert \le 1}\langle y, z\rangle .$ Let $d(x,A):=\inf _{x'\in A}\Vert x-x'\Vert$ be the distance from a point x to a set $A \subset \mathrm{I\!R}^n$. For two compact sets $A,B\subset \mathrm{I\!R}^n$, we write $\mathbb {D}(A,B):=\sup _{x\in A}d(x,B)$ for the deviation of A from B and $\mathbb {H}(A,B):=\max \{\mathbb {D}(A,B),$$\mathbb {D}(B,A)\}$ for the Hausdorff distance between A and B. We use $\mathbb {B}$ to denote the unit ball in a matrix or vector space. Finally, for a sequence of subsets $\{S_N\}$ in a metric space, denote by $\limsup _{N \rightarrow \infty } S_N$ its outer limit, that is,

$$\begin{aligned} \limsup _{N \rightarrow \infty } S_N:=\{x: \exists \,x_{N_k} \in S_{N_k} \text{ such } \text{ that }\, x_{N_k} \rightarrow x\, \text{ as }\, k \rightarrow \infty \}. \end{aligned}$$

2 Properties of DRSR

In this section, we investigate the properties of DRSR. It is easy to observe that $\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(Z)$ is the optimal value of the following minimization problem:

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{t \in \mathrm{I\!R}} &{}t\\ \text{ s.t. } &{}\displaystyle \sup _{P\in {\mathcal {P}}}{\mathbb {E}}_P[l(-Z-t)]\le \lambda . \end{array} \end{aligned}$$

(5)

The following proposition states that the DRSR is the worst-case SR and it preserves convexity of SR.

Proposition 1

Let $\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(Z)$ be defined as in (3), $Z\in L^{\infty }$ and $l:\mathrm{I\!R}\rightarrow \mathrm{I\!R}$ be a convex, increasing and non-constant function, let $\lambda$ be a pre-specified constant in the range of l. Then $\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(Z)$ is finite,

$$\begin{aligned} \text{ SR }_{l,\lambda }^{{\mathcal {P}}}(Z)=\sup _{P\in {\mathcal {P}}} \text{ SR }_{l,\lambda }^P(Z), \end{aligned}$$

(6)

and $\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(Z)$ is a convex risk measure.

Proof

Since Z is bounded, then there exist constants $\alpha ,\beta$ such that $Z(\omega )\in [\alpha ,\beta ]$ for all $\omega \in \varOmega$. Thus

$$\begin{aligned} l(-\beta -t) \le \sup _{P\in {\mathcal {P}}}{\mathbb {E}}_P[l(-Z-t)]\le l(-\alpha -t), \forall t\in \mathrm{I\!R}. \end{aligned}$$

Since $l(-\beta -t)\rightarrow \infty$ as $t\rightarrow -\infty$ and $l(-\alpha -t)\le \lambda$ for t sufficiently large, we conclude that the feasible set of problem (5) is bounded. To show equality (6), we note that

$$\begin{aligned} \hat{t}:= & {} \sup _{P\in {\mathcal {P}}} \text{ SR }_{l,\lambda }^P(Z) \le \inf _t \sup _{P\in {\mathcal {P}}} \{t\in \mathrm{I\!R}: {\mathbb {E}}_P [l(-Z-t)] \le \lambda \}\\\le & {} \inf _t \{t\in \mathrm{I\!R}: \sup _{P\in {\mathcal {P}}} {\mathbb {E}}_P[l(-Z-t)] \le \lambda \} =\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(Z)=: t^*. \end{aligned}$$

To show the converse inequality, note that $\hat{t} \ge \text{ SR }_{l,\lambda }^P(Z), \forall P\in {\mathcal {P}}.$ Thus

$$\begin{aligned} {\mathbb {E}}_P[l(-Z-\hat{t})] \le \lambda , \forall P\in {\mathcal {P}}, \end{aligned}$$

which implies $\hat{t}$ is a feasible solution of (5) and hence $t^*\le \hat{t}$. $\square$

Remark 1

It may be helpful to make some comments on Proposition 1.

• (i) The relationship established in (6) means that DRSR is the worst-case SR. This observation allows one to calculate DRSR via SR for each $P\in {\mathcal {P}}$ if it is easy to do so. Moreover, Giesecke et al. [15] showed that SR is a coherent risk measure if and only if the loss function l takes a specific form:

  $$\begin{aligned} l(z):=\lambda -\alpha [z]_- +\beta [z]_+, \,\beta \ge \alpha \ge 0, \end{aligned}$$

  where $[z]_-$ denotes the negative part of z and $[z]_+$ denotes the positive part. In this case, the SR gives rise to an expectile, see [3, Theorem 4.9]. Using this result, we can easily show through equation (6) that $\text{ DRSR }$ is a coherent risk measure when l takes the specific form in that the operation $\sup _{P\in {\mathcal {P}}}$ preserves positive homogeneity and subadditivity.

• (ii) The restriction of Z to $L^{\infty }$ implies that the support¹ of the probability distribution of Z is bounded. This condition may be relaxed to the case when there exist $t_l, t_u \in \mathrm{I\!R}$ such that $\sup _{P \in {\mathcal {P}}} {\mathbb {E}}_P[l(-Z-t_l)] >\lambda$ and $\sup _{P \in {\mathcal {P}}} {\mathbb {E}}_P[l(-Z-t_u)] < \lambda$, see [18].

We now move on to discuss the property of DRSR when it is applied to a random function. This is to pave a way for us to develop full investigation on (DRSRP) in Sects. 3 and 4. To this end, we need to make some assumptions on the random function $c(\cdot ,\cdot )$ and the loss function $l(\cdot )$. Throughout this section, we use $\varXi$ to denote the image space of random variable $\xi (\omega )$ and $\mathscr {P}(\varXi )$ to denote the set of all probability measures defined on the measurable space $(\varXi , \mathscr {B})$ with Borel sigma algebra $\mathscr {B}$. To ease notation, we will use $\xi$ to denote either the random vector $\xi (\omega )$ or an element of $\mathrm{I\!R}^k$ depending on the context.

Assumption 1

Let X, $l(\cdot )$ and $c(\cdot ,\cdot )$ be defined as in (DRSRP) (4). We assume the following. (a) X is a convex and compact set and $\varXi$ is a compact set, (b) l is convex, increasing, non-constant and Lipschitz continuous with modulus L, (c) $c(\cdot ,\xi )$ is finite valued, convex w.r.t. $x \in X$ for each $\xi \in \varXi$ and there exists a positive constant $\kappa$ such that

$$\begin{aligned} |c(x,\xi )-c(x,\xi ')| \le \kappa \Vert \xi -\xi '\Vert , \forall x\in X, \xi ,\xi '\in \varXi . \end{aligned}$$

The proposition below summarises some important properties of $l(c(x,\xi )-t)$ and $\displaystyle \sup \nolimits _{P\in {\mathcal {P}}}{\mathbb {E}}_P[l(c(x,\xi )-t)]-\lambda$ as a function of (x, t).

Proposition 2

Let $g(x,t,\xi ):=l(c(x,\xi )-t)$ and $v(x,t):=\displaystyle \sup \nolimits _{P\in {\mathcal {P}}}{\mathbb {E}}_P[{g(x,t,\xi )}]-\lambda$. The following assertions hold.

• (i) Under Assumption 1 (b) and (c), $g(\cdot ,\cdot ,\xi )$ is convex w.r.t. (x, t) for each fixed $\xi \in \varXi$, $g(x,t,\cdot )$ is uniformly Lipschitz continuous w.r.t. $\xi$ with modulus $L \kappa$, and v(x, t) is a convex function w.r.t. (x, t).

• (ii) If, in addition, Assumption 1 (a) holds and $\lambda$ is a pre-specified constant in the interior of the range of l, then there exist a point $(x_0,t_0) \in X \times \mathrm{I\!R}$ and a constant $\eta >0$ such that

  $$\begin{aligned} \displaystyle \sup _{P\in {\mathcal {P}}}{\mathbb {E}}_P[l(c(x_0,\xi )-t_0)]-\lambda <-\eta \end{aligned}$$

  (7)

  and $\text{(DRSRP) }$ has a finite optimal value.

Proof

• Part (i). It is well known that the composition of a convex function by a monotonic increasing convex function preserves convexity. The remaining claims can also be easily verified.

• Part (ii). Since $c(x,\xi )$ is finite valued and convex in x, it is continuous in x for each fixed $\xi$. Together with its uniform continuity in $\xi$, we are able to show that $c(x,\xi )$ is continuous over $X\times \varXi$. By the boundedness of X and $\varXi$, there is a positive constant $\alpha$ such that $c(x,\xi )\le \alpha$ for all $(x,\xi )\in X\times \varXi$. With the boundedness of c and the monotonic increasing, convex and non-constant property of l, we can easily show Part (ii) analogous to the proof of the first part of Proposition 1. We omit the details. $\square$

3 Structure of (DRSRP’) and approximation of the ambiguity set

In this section, we investigate the structure and numerical solvability of (DRSRP). Using the formulation (5) for DRSR, we can reformulate (DRSRP) as

$$\begin{aligned} {\hbox {(DRSRP')}} \quad \begin{array}{cl} \displaystyle \min _{x \in X,t \in T} &{} t\\ \text{ s.t. } \quad &{} \displaystyle \sup _{P\in {\mathcal {P}}}{\mathbb {E}}_P[l(c(x,\xi )-t)]\le \lambda , \end{array} \end{aligned}$$

(8)

where T is a compact set in $\mathrm{I\!R}$ which contains $t_0$ defined as in (7) and its existence is ensured by Proposition 2 under some moderate conditions. Obviously, the structure of (DRSRP’) is determined by the distributionally robust constraint. The latter relies heavily on the concrete structure of the ambiguity set ${\mathcal {P}}$ and the loss function l.

In the literature of distributionally robust optimization, various statistical methods have been proposed to build ambiguity sets based on available information of the underlying uncertainty, see for instance [27, 28] and the references therein. Here we consider $\phi$-divergence ball and Kantorovich ball approaches and discuss tractable formulations of the corresponding (DRSRP’).

3.1 Ambiguity set constructed through $\phi$-divergence

Let us now consider the case that the only available information about the random vector $\xi$ is its empirical data and the size of such data is limited (not very large). In stochastic programming, a well-known approach in such situation is to use empirical distribution constructed through the data to approximate the true probability distribution. However, if the sample size is not big enough or there is a reason from computational point of view to use a small size of empirical data (e.g., in multistage decision-making problems), then the quality of such approximation may be compromised. $\phi$-divergence is subsequently proposed to address this dilemma.

Let $p=(p_1,\ldots ,p_M)^T \in \mathrm{I\!R}^M_+$ and $q=(q_1,\ldots ,q_M)^T \in \mathrm{I\!R}^M_+$ be two probability vectors, that is, $\sum _{i=1}^M p_i =1$ and $\sum _{i=1}^M q_i=1$. The so-called $\phi$-divergence between p and q is defined as $I_{\phi }(p,q) :=\sum _{i=1}^M q_i \phi \left( \frac{p_i}{q_i}\right)$, where $\phi (t)$ is a convex function for $t \ge 0$, $\phi (1)=0$, $0 \phi (a/0):= a \lim _{t \rightarrow \infty } \phi (t)/t$ for $a>0$ and $0 \phi (0/0):=0$. In this subsection, we consider some common $\phi$-divergences which are defined as follows.

• (a) Kullback-Leibler: $I_{\phi _{KL}}(p,q)=\sum _i p_i \log \left( \frac{p_i}{q_i}\right)$ with $\phi _{KL}(t)=t \log t-t+1$;

• (b) Burg entropy: $I_{\phi _B}(p,q)=\sum _i q_i \log \left( \frac{q_i}{p_i}\right)$ with $\phi _B(t)=-\log t+t-1$;

• (c) J-divergence: $I_{\phi _J}(p,q)=\sum _i (p_i-q_i) \log \left( \frac{p_i}{q_i}\right)$ with $\phi _J(t)=(t-1) \log t$;

• (d) $\chi ^2$-distance: $I_{\phi _{\chi ^2}}(p,q)=\sum _i \frac{(p_i-q_i)^2}{p_i}$ with $\phi _{\chi ^2}(t)=\frac{1}{t} (t-1)^2$;

• (e) Modified $\chi ^2$-distance: $I_{\phi _{m\chi ^2}}(p,q)=\sum _i \frac{(p_i-q_i)^2}{q_i}$ with $\phi _{m\chi ^2}(t)= (t-1)^2$;

• (f) Hellinger distance: $I_{\phi _H}(p,q)=\sum _i (\sqrt{p_i}-\sqrt{q_i})^2$ with $\phi _H(t)=(\sqrt{t}-1)^2$;

• (g) Variation distance: $I_{\phi _V}(p,q)=\sum _i |p_i-q_i|$ with $\phi _V(t)=|t-1|$.

Lemma 1

(Relationships between $\phi$-divergences) For two probability vectors $p,q \in \mathrm{I\!R}^M_+$, the following inequalities hold.

• (i) $I_{\phi _V}(p,q) \le \min \left( \sqrt{2I_{\phi _{KL}}(p,q)}, \sqrt{2I_{\phi _{B}}(p,q)},\sqrt{I_{\phi _{J}}(p,q)}, \sqrt{I_{\phi _{\chi ^2}}(p,q)},\right.$

  $\left. \sqrt{I_{\phi _{m\chi ^2}}(p,q)}\right) ;$

• (ii) $I_{\phi _H}(p,q) \le I_{\phi _V}(p,q) \le 2\sqrt{I_{\phi _H}(p,q)}$.

We omit the proof as the results can be easily derived by the divergence functions $\phi$.

Let $\{\zeta ^1,\ldots , \zeta ^M\} \subset \varXi$ denote the M-distinct points in the support of $\xi$ and $\varXi _i$ denote the Voronoi partition of $\varXi$ centered at $\zeta ^i$ for $i=1,\ldots ,M$. Let $\xi ^1,\ldots ,\xi ^N$ be an iid sample of $\xi$ where $N>>M$ and $N_i$ denote the number of samples falling into area $\varXi _i$. Define empirical distribution

$$\begin{aligned} P_N(\cdot ) := \sum _{i=1}^M \frac{N_i}{N} \mathbb {1}_{\zeta ^i}(\cdot ), \end{aligned}$$

(9)

and ambiguity set

$$\begin{aligned} {\mathcal {P}}_N^M :=\left\{ \sum _{i=1}^M p_i \mathbb {1}_{\zeta ^i}(\cdot ): I_{\phi }(p,p_N)\le r, \sum _{i=1}^M p_i =1, p_i\ge 0, \forall i=1,\ldots ,M \right\} ,\qquad \end{aligned}$$

(10)

where $p_N= \left( \frac{N_1}{N},\ldots , \frac{N_M}{N} \right) ^T$. Using ${\mathcal {P}}_N^M$ for the ambiguity set in (DRSRP’), we can derive a dual formulation of (DRSRP’) as follows:

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x \in X,t \in T, \tau ,u} &{} t\\ \text{ s.t. } &{}\displaystyle \tau + r u +u \sum _{i=1}^M [p_N]_i \phi ^*(s_i)\le \lambda ,\\ &{}\displaystyle s_i \le \lim _{t \rightarrow \infty } \frac{\phi (t)}{t},\,\, i=1,\ldots ,M,\\ &{}s_i=[l(c(x,\zeta ^i)-t)-\tau ]/u, \,\, i=1,\ldots ,M,\\ &{}u \ge 0, \end{array} \end{aligned}$$

(11)

where $p_N$ is defined as in (10) and we write $[p_N]_i$ for the ith component of $p_N$, $\phi ^*$ denotes the Fenchel conjugate of $\phi$, i.e., $\phi ^*(s)=\sup _{t \ge 0} \{st-\phi (t)\}$, see similar formulation in [4]. Note that $u\sum _{i=1}^M [p_N]_i \phi ^*([l(c(x,\zeta ^i)-t)-\tau ]/u)$ is a convex function of $x,u,\tau$ and t, see [19]. Thus, problem (11) is a convex program.

It is important to note that the reformulation (11) relies heavily on the discrete structure of the nominal distribution. Note that it is possible to use a continuous distribution for the nominal distribution, in which case the summation in the first constraint of problem (11) will become ${\mathbb {E}}[\phi ^*([l(c(x,\zeta )-t)-\tau ]/u)]$ (before introducing new variables $s_i$). In such a case, we will need to use SAA approach to deal with the expected value.

The reallocation of the probabilities through Voronoi partition provides an effective way to reduce the scenarios of the discretized problem and hence the size of problem (11). It remains to be explained how the ambiguity set approximates the true probability distribution.

Let $\mathscr {L}$ denote the set of functions $h:\varXi \rightarrow \mathrm{I\!R}$ satisfying $|h(\xi _1)-h(\xi _2)|\le \Vert \xi _1-\xi _2\Vert$, and $P,Q \in \mathscr {P}(\varXi )$ be two probability measures. Recall that the Kantorovich metric (or distance) between P and Q, denoted by $\mathsf {dl}_K(P,Q)$, is defined by

$$\begin{aligned} \mathsf {dl}_K(P,Q):=\sup _{h \in \mathscr {L}} \left\{ \int _{\varXi } h(\xi )P (d \xi )- \int _{\varXi } h(\xi )Q (d \xi ) \right\} . \end{aligned}$$

Using the Kantorovich metric, we can define the deviation of a set of probability measures ${\mathcal {P}}$ from another set of probability measures ${\mathcal {Q}}$ by $\mathbb {D}_K({\mathcal {P}},{\mathcal {Q}}) := \sup _{P\in {\mathcal {P}}}\inf _{Q\in {\mathcal {Q}}} \mathsf {dl}_K(P,Q),$ and the Hausdorff distance between the two sets by $\mathbb {H}_K({\mathcal {P}},{\mathcal {Q}}) := \max \left\{ \mathbb {D}_K({\mathcal {P}},{\mathcal {Q}}), \mathbb {D}_K({\mathcal {Q}},{\mathcal {P}})\right\} .$ An important property of the Kantorovich metric is that it metrizes weak convergence of probability measures [5] when the support is bounded, that is, a sequence of probability measures $\{P_N\}$ converges to P weakly if and only if $\mathsf {dl}_K(P_N,P)\rightarrow 0$ as N tends to infinity.

Recall that for a given set of points $\{\zeta ^1,\ldots , \zeta ^M\}$, the Voronoi partition of $\varXi$ is defined as M subsets of $\varXi$, denoted by $\varXi _1,\ldots ,\varXi _M$, with $\bigcup _{i=1,\ldots ,M} \varXi _i=\varXi$ and $\varXi _i \subseteq \left\{ y\in \varXi :\Vert y-\zeta ^i\Vert =\min _{j=1,\ldots ,M} \Vert y-\zeta ^j\Vert \right\} .$ By [22, Lemma 4.9],

$$\begin{aligned} \mathsf {dl}_K\left( \sum _{i=1}^M P^*(\varXi _i) \mathbb {1}_{\zeta ^i}(\cdot ), P^* \right)= & {} \int \min _{1 \le i \le M} d(\xi ,\zeta ^i) d P^*\nonumber \\= & {} \sum _{i=1}^M \int _{\varXi _i} d(\xi ,\zeta ^i) d P^* \le \beta _M, \end{aligned}$$

(12)

where

$$\begin{aligned} \beta _M:= \max _{\xi \in \varXi } \min _{1 \le i \le M}d(\xi ,\zeta ^i). \end{aligned}$$

(13)

Using this, we can estimate the Kantorovich distance between ${\mathcal {P}}_N^M$ and the true probability distribution $P^*$.

Proposition 3

Let ${\mathcal {P}}_N^M$ be defined as in (10) and $P^*$ be the true probability distribution of $\xi$. Let $\beta _M$ be defined as in (13) and $\delta$ be a positive number such that $M \delta < 1$. If $\phi$ is chosen from one of the functions listed in (a)-(g) preceding Lemma 1, then with probability at least $1-M\delta$,

$$\begin{aligned} \mathbb {H}_K({\mathcal {P}}_N^M, P^*) \le \beta _M+\frac{D}{2} \max \{2\sqrt{r},r\}&+ \frac{D}{2} \varDelta (M,N,\delta ), \end{aligned}$$

(14)

where $\varDelta (M,N,\delta ):=\min \left( \frac{M}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) , 4+ \frac{1}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) \right)$, D is the diameter of $\varXi$, that is, $\sup \{\Vert \xi '-\xi ''\Vert : \xi ',\xi ''\in \varXi \}$, and r is defined as in (10). In the case when $\xi$ follows a discrete distribution with support $\{\zeta ^1,\ldots , \zeta ^M\}$, we have

$$\begin{aligned} \mathbb {H}_K({\mathcal {P}}_N^M, P^*) \le \frac{D}{2}\max \{2\sqrt{r},r\}+ {\frac{D}{2} \varDelta (M,N,\delta )} \end{aligned}$$

(15)

with probability at least $1-M\delta$.

Proof

By the triangle inequality of the Hausdorff distance with the Kantorovich metric,

$$\begin{aligned} \mathbb {H}_K({\mathcal {P}}_N^M, P^*) \le \sup _{P\in {\mathcal {P}}_N^M} \mathsf {dl}_K\left( P,\sum _{i=1}^M P^*(\varXi _i) \mathbb {1}_{\zeta ^i}(\cdot ) \right) + \mathsf {dl}_K\left( \sum _{i=1}^M P^*(\varXi _i) \mathbb {1}_{\zeta ^i}(\cdot ), P^* \right) . \end{aligned}$$

By (12), $\mathsf {dl}_K\left( \sum _{i=1}^M P^*(\varXi _i) \mathbb {1}_{\zeta ^i}(\cdot ), P^* \right) \le \beta _M.$ Moreover, it follows by [14, Theorem 4], the Kantorovich distance is bounded by D / 2 times the total variation distance, that is,

$$\begin{aligned} \mathsf {dl}_K\left( P,\sum _{i=1}^M P^*(\varXi _i) \mathbb {1}_{\zeta ^i}(\cdot )\right) \le \frac{D}{2} \sum _{i=1}^M \left| p_i-P^*(\varXi _i) \right| . \end{aligned}$$

Observe that

$$\begin{aligned} \sum _{i=1}^M \left| p_i-P^*(\varXi _i) \right|\le & {} \sum _{i=1}^M \left( \left| p_i-[p_N]_i\right| + \left| [p_N]_i-P^*(\varXi _i)\right| \right) \nonumber \\= & {} I_{\phi _V}(p,p_N) + \sum _{i=1}^M \left| [p_N]_i-P^*(\varXi _i)\right| . \end{aligned}$$

By Lemma 1,

$$\begin{aligned} I_{\phi _V}(P_N^M,p_N) \le \max \left\{ 2 \sqrt{I_{\phi }(P_N^M,p_N)}, I_{\phi _V}(P_N^M,p_N)\right\} \le \max \{2\sqrt{r},r\}. \end{aligned}$$

Thus, in order to show (14), it suffices to show

$$\begin{aligned} \sum _{i=1}^M \left| [p_N]_i-P^*(\varXi _i)\right| \le \varDelta (M,N,\delta ). \end{aligned}$$

(16)

Let $a \in \mathrm{I\!R}^M$ be a vector with $\Vert a\Vert _\infty :=\max _{1\le i \le M} |a_i|=1$, and $\phi _a(\xi ):= \sum _{i=1}^M a_i\mathbb {1}_{\varXi _i}(\xi )$. Then $\sup _{\xi \in \varXi }|\phi _a(\xi )|\le 1$ and it follows by [25, Theorem 3] that

$$\begin{aligned} \left| \frac{1}{N}\sum _{k=1}^N \phi _a(\xi ^k)-{\mathbb {E}}_{P^*}[\phi _a(\xi )]\right| \le \frac{1}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) \end{aligned}$$

(17)

with probability at least $1-\delta$ for the fixed a. In particular, if we set $a=e_i$, for $i=1,\ldots ,M$, where $e_i\in \mathrm{I\!R}^M$ is a vector with ith component being 1 and the rest being 0, then we obtain

$$\begin{aligned} \left| [p_N]_i-P^*(\varXi _i)\right| = \left| \frac{1}{N}\sum _{k=1}^N \phi _{e_i}(\xi ^k)-{\mathbb {E}}_{P^*}[\phi _{e_i}(\xi )]\right| \le \frac{1}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) \nonumber \\ \end{aligned}$$

(18)

with probability at least $1-\delta$ for each $i=1,\cdots ,M$. By Bouferroni’s inequality,

$$\begin{aligned} \sum _{i=1}^M \left| [p_N]_i-P^*(\varXi _i)\right| \le \frac{M}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) \end{aligned}$$

(19)

with probability at least $1-M\delta$ and hence we have shown (16) for the first part of its bound in $\varDelta (M,N,\delta )$.

To show the second part of the bound, we need a bit more complex argument to estimate the left hand side of (16). Let $A :=\{a\in \mathrm{I\!R}^M: \Vert a\Vert _\infty =1\}$. For a small positive number $\nu$ (less or equal to 2), let $A_k:=\{a^1,\cdots ,a^k\}$ be such that for any $a\in A$, there exists a point $a^i(a)\in A_k$ depending on a such that $\Vert a- a^i(a)\Vert _\infty \le \nu$, i.e., $A_k=\{a^1,\cdots ,a^k\}$ is a $\nu$-net of A. Observe that

$$\begin{aligned} \sum _{i=1}^M \left| [p_N]_i-P^*(\varXi _i)\right| = \sup _{\Vert a\Vert _\infty =1} |p_N^T a-{p^*}^T a|, \end{aligned}$$

(20)

where we write $p^*$ for the M-dimensional vector with i component $P^*(\varXi _i)$. Then

$$\begin{aligned} |p_N^T a-{p^*}^T a|\le & {} |p_N^T (a-a^i(a))|+ |p_N^T a^i(a) - {p^*}^Ta^i(a)| +| {p^*}^T a^i(a)-{p^*}^T a|\nonumber \\\le & {} 2\nu + |p_N^T a^i(a) - {p^*}^T a^i(a)|. \end{aligned}$$

By (17), for each $a^i$, $i=1,\cdots ,k$

$$\begin{aligned} |p_N^T a^i - {p^*}^T a^i| \le \frac{1}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) \end{aligned}$$

(21)

with probability at least $1-\delta$, thus inequality (21) holds uniformly for all $i=1,\cdots ,k$ with probability at least $1-k\delta$. This enables us to conclude that

$$\begin{aligned} \sum _{i=1}^M \left| [p_N]_i-P^*(\varXi _i)\right|= & {} \sup _{\Vert a\Vert _\infty =1}|p_N^T a-{p^*}^T a| \nonumber \\\le & {} 2\nu + \frac{1}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) \end{aligned}$$

(22)

with probability at least $1-k\delta$. Since when $\nu =2$, $A_k$ will be a trivial $\nu$-net, then we can set $k=M$ and obtain from (22) that

$$\begin{aligned} \sum _{i=1}^M \left| [p_N]_i-P^*(\varXi _i)\right| \le 4+ \frac{1}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) \end{aligned}$$

(23)

with probability at least $1-M\delta$. This completes the proof of (16) and hence inequality (14).

In the case when $\xi$ follows a discrete distribution with support $\{\zeta ^1,\ldots , \zeta ^M\}$,

$$\begin{aligned} \mathbb {H}_K({\mathcal {P}}_N^M, P^*) \le \sup _{P \in {\mathcal {P}}_N^M} \frac{D}{2}\left( I_{\phi _V}(P,p_N) + \sum _{i=1}^M \left| [p_N]_i-P^*(\varXi _i)\right| \right) . \end{aligned}$$

The rest follows from similar analysis for the proof of (14). $\square$

It might be helpful to make a few comments on the above technical results. First, if we set $\delta =\frac{1}{10M}$, then $1-\delta M =90\%$ and the third term at the right hand side of (14) is

$$\begin{aligned} \frac{D}{2}\min \left( \frac{M}{\sqrt{N}}\left( 2+\sqrt{2 \ln (10M)}\right) , 4+ \frac{1}{\sqrt{N}}\left( 2+\sqrt{2 \ln (10M)}\right) \right) . \end{aligned}$$

(24)

In order for the first part of (24) to be small, N must be significantly larger than M. The approach works for the case when there is a large data set which is not scattered evenly over $\varXi$, but rather they form clumps, locally dense areas, modes, or clusters. In the case that N is less than $(M-1)^2$, the second part of (24) is smaller than the first part, which means the second part provides a lower bound. Second, the true distribution in the local areas may be further described by moment conditions, see [20, 27]. Third, Pflug and Pichler proposed a practical way for identifying the optimal location of discrete points $\zeta ^1,\ldots ,\zeta ^M$ and computing the probability of each Voronoi partition, see [22, Algorithms 4.1–4.5]. Forth, the inequality (14) gives a bound for the Hausdorff distance of the true probability distribution $P^*$ and the ambiguity set ${\mathcal {P}}_N^M$, it does not indicate the true probability distribution $P^*$ being located in ${\mathcal {P}}_N^M$.

Since the ambiguity set ${\mathcal {P}}_N^M$ does not constitute any continuous distribution irrespective of $r>0$, then when the true probability distribution $P^*$ is continuous, $P^*$ lies outside ${\mathcal {P}}_N^M$ with probability 1. If the true probability distribution $P^*$ is discrete, Pardo [21] showed that the estimated $\phi$-divergence $\frac{2N}{\phi ''(1)} I_{\phi }(p^*,p_N)$ asymptotically follows a $\chi _{M-1}^2$-distribution with $M-1$ degrees of freedom, where $p^*$ denotes the probability vector corresponding to probability measure $P^*$ and M is the cardinality of $\varXi$ (the support of $P^*$), which means if we set

$$\begin{aligned} r:=\frac{\phi ''(1)}{2N} \chi _{M-1,1-\delta }^2, \end{aligned}$$

(25)

then with probability $1-\delta$, $I_{\phi }(p^*,p_N) \le r$. The latter indicates that the ambiguity set (10) lies in the $1-\delta$ confidence region.

For general $\phi$-divergences, we are unable to establish the quantitative convergence as in Proposition 3. However, if $P^*$ follows a discrete distribution with support $\{\zeta ^1,\ldots , \zeta ^M\}$, the following qualitative convergence result holds.

Proposition 4

[19, Proposition 2] Suppose that $\phi (t) \ge 0$ has a unique root at $t=1$ and the samples are independent and identically distributed from the true distribution $P^*$. Then $\mathbb {H}_K({\mathcal {P}}_N^M,P^*)\rightarrow 0, \text{ w.p.1 },$ as $N \rightarrow \infty$, where r is defined as in (25).

Note that in [19, Proposition 2] the convergence is established under the total variation metric, since the probability distributions here are discrete, the convergence is equivalent to that under the Kantorovich metric. We refer readers to [19] for the details of the proof.

3.2 Kantorovich ball

An alternative approach to the $\phi$-divergence ball is to consider Kantorovich ball centered at a nominal distribution, that is,

$$\begin{aligned} {\mathcal {P}}_N=\{P \in \mathscr {P} (\varXi ): \mathsf {dl}_K(P,P_N) \le r\}, \end{aligned}$$

(26)

where $P_N(\cdot )=\frac{1}{N} \sum _{i=1}^N \mathbb {1}_{\xi ^i}(\cdot )$ with $\xi ^1,\ldots ,\xi ^N$ being iid samples of $\xi$. Differing from the $\phi$-divergence ball, the Kantorovich ball contains both discrete and continuous distributions. In particular, if there exists a positive number $a>0$ such that

$$\begin{aligned} \theta :=\int _{\varXi } \exp (\Vert \xi \Vert ^a) P^* (d \xi ) < \infty , \end{aligned}$$

(27)

then for any $r>0$, there exist positive constants $C_1$ and $C_2$ such that

$$\begin{aligned} \text{ Prob }(\mathsf {dl}_K(P^*,P_N) \ge r) \le \left\{ \begin{array}{ll} C_1\exp (-C_2 N r^{\max \{k,2\}}) &{}\text{ if }\, r \le 1,\\ \exp (-C_2 N r^a) &{}\text{ if }\, r > 1,\\ \end{array} \right. \end{aligned}$$

(28)

for all $N \ge 1$, $k\ne 2$, where $C_1$ and $C_2$ are positive constants only depending on a, $\theta$ and k, “Prob” is a probability distribution over space $\varXi \times \cdots \times \varXi$ (N times) with Borel-sigma algebra $\mathscr {B} \otimes \cdots \otimes \mathscr {B}$, and k is the dimension of $\xi$, see [11] for details. By setting the right hand side of the above inequality to $\delta$ and solving for r, we may set

$$\begin{aligned} r_N(\delta ):= \left\{ \begin{array}{ll} \left( \frac{\log (C_1\delta ^{-1})}{C_2 N}\right) ^{1/{\max \{k,2\}}} &{}\text{ if }\,N \ge \frac{\log (C_1\delta ^{-1})}{C_2},\\ \left( \frac{\log (C_1\delta ^{-1})}{C_2 N}\right) ^{1/a} &{}\text{ if }\,N < \frac{\log (C_1\delta ^{-1})}{C_2}, \end{array} \right. \end{aligned}$$

(29)

and consequently the ambiguity set (26) contains the true probability distribution $P^*$ with probability $1- \delta$ when $r=r_N(\delta )$.

In [8, 13, 29], the dual formulation of distributionally robust optimization problem with the ambiguity set (26) has been established. Based on these results, the dual of (DRSRP’) can be written as

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x \in X,t \in T,\eta ,s} &{}t\\ \text{ s.t. } &{}\displaystyle \eta r+\frac{1}{N} \sum _{i=1}^N s_i \le \lambda ,\\ &{}\displaystyle \sup _{\xi \in \varXi } \left[ l(c(x,\xi )-t)-\eta \Vert \xi -\xi ^i\Vert \right] \le s_i, i=1,\ldots ,N. \end{array} \end{aligned}$$

(30)

In the case when $c(x,\xi )=-x^T\xi$, $\varXi =\{\xi \in \mathrm{I\!R}^k: G \xi \le d\}$ and

$$\begin{aligned} l(c(x,\xi )-t)= \displaystyle \max _{j=1,\ldots ,K} a_j(-x^T \xi -t)+b_j= \displaystyle \max _{j=1,\ldots ,K} \langle -a_j x,\xi \rangle -a_j t+b_j, \end{aligned}$$

problem (30) can be recast as

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x \in X,t \in T,\eta ,s,\gamma _{ij}} &{}t\\ \text{ s.t. } &{}\displaystyle \eta r+\frac{1}{N} \sum _{i=1}^N s_i \le \lambda ,\\ &{}b_j-a_j t-\langle a_j x,\xi _i \rangle +\langle \gamma _{ij}, d-G \xi ^i \rangle \le s_i,\\ &{} i=1,\ldots , N, j=1,\ldots , K,\\ &{}\Vert G^T \gamma _{ij}+a_j x\Vert _*\le \eta ,\, i=1,\ldots , N, j=1,\ldots , K,\\ &{}\gamma _{ij} \ge 0, \, i=1,\ldots , N, j=1,\ldots , K. \end{array} \end{aligned}$$

The proposition below gives a bound for the Hausdorff distance of ${\mathcal {P}}_N$ and $P^*$ under the Kantorovich metric.

Proposition 5

Let ${\mathcal {P}}_N$ be defined as in (26) and $P^*$ denote the true probability distribution. Let $r_N(\delta )$ be defined as in (29). If the radius of the Kantorovich ball in (26) is equal to $r_N(\delta )$, then with probability at least $1-\delta$,

$$\begin{aligned} \mathbb {H}_K({\mathcal {P}}_N,P^*) \le 2r_N(\delta ). \end{aligned}$$

(31)

Proof

We first prove that

$$\begin{aligned} \mathbb {H}_K({\mathcal {P}}_N, P^*)\le \mathsf {dl}_K(P_N,P^*) +r. \end{aligned}$$

(32)

To see this, for any $P' \in {\mathcal {P}}_N$, we have

$$\begin{aligned} \mathsf {dl}_K(P',P^*) \le \mathsf {dl}_K(P',P_N)+\mathsf {dl}_K(P_N,P^*) \le r +\mathsf {dl}_K(P_N,P^*), \end{aligned}$$

which implies $\mathbb {D}_K({\mathcal {P}}_N,P^*) \le r +\mathsf {dl}_K(P_N,P^*).$ On the other hand,

$$\begin{aligned} \mathbb {D}_K(P^*,{\mathcal {P}}_N)= \inf _{Q \in {\mathcal {P}}_N} \mathsf {dl}_K(P^*,Q) \le \mathsf {dl}_K(P^*,P') \le r+\mathsf {dl}_K(P_N,P^*). \end{aligned}$$

A combination of the last two inequalities yields (32).

Let us now estimate the first term in (32), i.e., $\mathsf {dl}_K(P_N,P^*)$. By the definition of $r_N(\delta )$, we have with probability $1-\delta$, $\mathsf {dl}_K(P_N,P^*) \le r_N(\delta )$. The conclusion follows. $\square$

In the case when the centre of the Kantorovich ball $P_N$ in (26) is replaced by that defined as in (9), we have

$$\begin{aligned} \mathbb {H}_K({\mathcal {P}}_N,P^*) \le \beta _M+ r+\frac{D}{2}\varDelta (M,N,\delta ) \end{aligned}$$

(33)

with probability at least $1-M\delta$, where $\varDelta (M,N,\delta )$ is defined as in Proposition 3. To see this, we can use the triangle inequality of the Hausdorff distance with the Kantorovich metric to derive

$$\begin{aligned}&\mathbb {H}_K({\mathcal {P}}_N, P^*) \nonumber \\&\quad \le \sup _{P\in {\mathcal {P}}_N} \mathsf {dl}_K\left( P,\sum _{j=1}^M P^*(\varXi _j) \mathbb {1}_{\zeta ^j}(\cdot ) \right) + \mathsf {dl}_K\left( \sum _{j=1}^M P^*(\varXi _j) \mathbb {1}_{\zeta ^j}(\cdot ), P^* \right) .\qquad \end{aligned}$$

(34)

Since

$$\begin{aligned} \mathsf {dl}_K\left( P,\sum _{j=1}^M P^*(\varXi _j) \mathbb {1}_{\zeta ^j}(\cdot )\right)\le & {} \mathsf {dl}_K\left( P,P_N\right) +\mathsf {dl}_K\left( P_N,\sum _{j=1}^M P^*(\varXi _j) \mathbb {1}_{\zeta ^j}(\cdot )\right) \nonumber \\\le & {} r + \frac{D}{2}\sum _{j=1}^M \left| [p_N]_j-P^*(\varXi _j)\right| , \end{aligned}$$

(35)

we establish (33) by combining (34), (35), (12), (19) and (23).

Before concluding this section, we note that it is possible to use other statistical methods for constructing the ambiguity sets such as moment conditions and mixture distribution, we omit them due to limitation of the length of the paper, interested readers may find them in [16] and references therein.

4 Convergence of (DRSRP’)

In Sect. 3, we discussed two approaches for constructing the ambiguity set of the (DRSRP’) model, each of which is defined through iid samples.

Let us rewrite the model with ${\mathcal {P}}$ being replaced by ${\mathcal {P}}_N$:

$$\begin{aligned} {\hbox {(DRSRP'-N)}} \quad \left\{ \begin{array}{cl} \displaystyle \min _{X \in X, t \in T} &{}t\\ \text{ s.t. } &{}\displaystyle \sup _{P\in {\mathcal {P}}_N}{\mathbb {E}}_P[l(c(x,\xi )-t)]\le \lambda , \end{array} \right. \end{aligned}$$

(36)

to explicitly indicate the dependence of the samples. In this section, we investigate finite sample guarantees on the quality of the optimal solutions obtained from solving ${\hbox {(DRSRP'-N)}}$, a concept proposed by Esfahani and Kuhn [8], as well as convergence of the optimal values as the sample size increases.

Let $x_N$ be a solution of distributionally robust shortfall risk minimization problem (DRSRP’N), let ${\vartheta }_N$ be the optimal value and $S_N$ the corresponding optimal solution set. The out-of-sample performance of $x_N$ is defined as $\text{ SR }^{P^*}_{l,\lambda }(-c(x_N,\xi ))$, where $P^*$ is the true probability distribution. Since $P^*$ is unknown, the exact out-of-sample performance of $x_N$ cannot be computed, but we may seek its upper bound $\vartheta _N$ such that

$$\begin{aligned} \text{ Prob }(\text{ SR }^{P^*}_{l,\lambda }(-c(x_N,\xi )) \le {\vartheta }_N) \ge 1-\delta , \end{aligned}$$

(37)

where $\delta \in (0,1)$. Following the terminology of Esfahani and Kuhn [8], we call $\delta$ a significance parameter and $\vartheta _N$ the certificate for the out-of-sample performance. The probability on the left-hand side of (37) indicates ${\vartheta }_N$’s reliability. The following theorem states that the finite sample guarantee condition is fulfilled for the ambiguity sets discussed in Sect. 3, that is, when the size of the ambiguity sets are chosen carefully, the certificate ${\vartheta }_N$ can provide a $1-\delta$ confidence bound of the type (37) on the out-of-sample performance of $x_N$.

Theorem 1

(Finite sample guarantee) The following assertions hold:

• (i) Suppose the true probability distribution $P^*$ is discrete, i.e., $\varXi =\{\zeta ^1,\ldots ,\zeta ^M\}$. Let ${\mathcal {P}}_N^M$ be defined as (10) with r being given as (25), then with ${\mathcal {P}}_N={\mathcal {P}}_N^M$, the finite sample guarantee (37) holds.

• (ii) Let ${\mathcal {P}}_N$ be defined as in (26) with $r=r_N(\delta )$ being given in (29). Under condition (27), the finite sample guarantee (37) holds.

Proof

The results follow straightforwardly from (25), (28), (29) and the definition of finite sample guarantee. $\square$

We now move on to investigate convergence of ${\vartheta }_N$ and $S_N$. From the discussion in Sect. 3, we know that $\mathbb {H}_K({\mathcal {P}}_N,P^*)\rightarrow 0$. However, to broaden the coverage of the convergence results, we present them by considering a slightly more general case with $P^*$ being replaced by a set ${\mathcal {P}}^*$.

Theorem 2

(Convergence of the optimal values and optimal solutions) Let ${\mathcal {P}}^*\subset \mathscr {P}(\varXi )$ be such that $\lim _{N\rightarrow \infty } \mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}^*)=0.$ Let ${\vartheta }^*$ denote the optimal value of ${\hbox {(DRSRP')}}$ with ${\mathcal {P}}$ being replaced by ${\mathcal {P}}^*$. Let $S^*$ be the corresponding optimal solutions. Under Assumption 1,

$$\begin{aligned} |{\vartheta }_N-{\vartheta }^*| \le \frac{2 D_XL \kappa }{\eta } \mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}^*) \end{aligned}$$

(38)

for N sufficiently large and

$$\begin{aligned} \displaystyle \limsup _{N \rightarrow \infty } S_N=S^*, \end{aligned}$$

(39)

where $D_X$ denotes the diameter of X, $\eta$ is defined as in Proposition 2, and $L, \kappa$ are defined as in Assumption 1.

Proof

Let $v^*(x,t):=\sup _{P\in {\mathcal {P}}^*}{\mathbb {E}}_P[l(c(x,\xi )-t)]- \lambda$ and $v_N(x,t):=\sup _{P\in {\mathcal {P}}_N}$${\mathbb {E}}_P[l(c(x,\xi )-t)]- \lambda .$ Let $g(x,t,\xi ):=l(c(x,\xi )-t)$. By the definition,

$$\begin{aligned} v_N(x,t)-v^*(x,t)= & {} \sup _{P\in {\mathcal {P}}_N}{\mathbb {E}}_P[g(x,t,\xi )]-\sup _{Q\in {\mathcal {P}}^*}{\mathbb {E}}_Q[g(x,t,\xi )]\\= & {} \sup _{P\in {\mathcal {P}}_N} \inf _{Q\in {\mathcal {P}}^*} ({\mathbb {E}}_P[g(x,t,\xi )]-{\mathbb {E}}_Q[g(x,t,\xi )])\\\le & {} \sup _{P\in {\mathcal {P}}_N} \inf _{Q\in {\mathcal {P}}^*} L\kappa \mathsf {dl}_K(P,Q)= L \kappa \mathbb {D}_K({\mathcal {P}}_N,{\mathcal {P}}^*), \end{aligned}$$

where the inequality is due to equi-Lipschitz continuity of g in $\xi$ and the definition of the Kantorovich metric. Likewise, we can establish

$$\begin{aligned} v^*(x,t)-v_N(x,t) \le L \kappa \mathbb {D}_K({\mathcal {P}}^*,{\mathcal {P}}_N). \end{aligned}$$

Combining the above two inequalities, we obtain

$$\begin{aligned} \displaystyle \sup _{x\in X, t\in T} |v_N(x,t)-v^*(x,t)| \le L\kappa \mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}^*). \end{aligned}$$

(40)

Let ${\mathcal {F}}^*:=\{(x,t) \in X \times T: v^*(x,t) \le \lambda \}$ and ${\mathcal {F}}_N:=\{(x,t) \in X \times T: v_N(x,t) \le \lambda \}$. By Proposition 2, $v^*$ and $v_N$ are convex on $X\times T$. Moreover, the Slater condition (7) allows us to apply Robinson’s error bound for the convex inequality system (see [23]), i.e., there exists a positive constant $C_1$ such that for any $(x,t) \in X \times T$, $d((x,t),{\mathcal {F}}^*) \le C_1[v^*(x,t)-\lambda ]_+$. Let $(x,t) \in {\mathcal {F}}_N$. The inequality above enables us to estimate

$$\begin{aligned} d((x,t),{\mathcal {F}}^*)\le & {} C_1[v^*(x,t)-\lambda ]_+\nonumber \\\le & {} C_1(|v^*(x,t)-v_N(x,t)|+[v_N(x,t)-\lambda ]_+)\nonumber \\= & {} C_1|v^*(x,t)-v_N(x,t)| \le C_1 L \kappa \mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}^*). \end{aligned}$$

(41)

The last inequality follows from (40) and Robinson’s error bound [23] ensures that the constant $C_1$ is bounded by $D_X/\eta$, where $D_X$ is the diameter of X. This shows $\mathbb {D}({\mathcal {F}}_N,{\mathcal {F}}^*) \le \frac{D_X L \kappa }{\eta } \mathbb {H}_K({\mathcal {P}}^*,{\mathcal {P}}_N).$ On the other hand, the uniform convergence of $v_N$ to v ensures $v_N(x_0,t_0)-\lambda <-\eta /2$ for N sufficiently large, which means the convex inequality $v_N(x,t) -\lambda \le 0$ satisfies the Slater condition. By applying Robinson’s error bound for the inequality, we obtain

$$\begin{aligned} d((x,t),{\mathcal {F}}_N) \le C_2|v^*(x,t)-v_N(x,t)| \le C_2L \kappa \mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}^*) \end{aligned}$$

(42)

for $(x,t) \in {\mathcal {F}}^*$ and N is sufficiently large, where $C_2$ is bounded by $2 D_X/\eta$. Combining (41) and (42), we obtain

$$\begin{aligned} {\mathbb {H}}({\mathcal {F}}_N,{\mathcal {F}}^*) \le \frac{2 D_XL \kappa }{\eta } \mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}^*). \end{aligned}$$

(43)

Let $(x^*,t^*)$ be an optimal solution to (DRSRP’) with ${\mathcal {P}}$ being replaced by ${\mathcal {P}}^*$ and $(x_N,t_N)$ the optimal solution of (DRSRP’-N). Note that ${\mathcal {F}}_N,{\mathcal {F}}^*\subset X\times T$. Let $\mathrm{\Pi }_T {\mathcal {F}}:= \{t\in T: \text{ there } \text{ exists } \; x\in X \; \text{ such } \text{ that }\; (x,t) \in {\mathcal {F}}\}.$ Since $t_N =\min \{ t: t\in \mathrm{\Pi }_T {\mathcal {F}}_N\}$ and $t^* =\min \{ t: t\in \mathrm{\Pi }_T {\mathcal {F}}^*\}$, then

$$\begin{aligned} |t_N-t^*| \le {\mathbb {H}}({\mathrm{\Pi }_T {\mathcal {F}}_N},\mathrm{\Pi }_T {\mathcal {F}}^*). \end{aligned}$$

Thus

$$\begin{aligned} |{\vartheta }_N-{\vartheta }^*|=|t_N-t^*| \le {\mathbb {H}}({\mathrm{\Pi }_T {\mathcal {F}}_N},\mathrm{\Pi }_T {\mathcal {F}}^*) \le {\mathbb {H}}({{\mathcal {F}}_N},{\mathcal {F}}^*), \end{aligned}$$

which yields (38) via (43).

Now, we move on to show (39). Let $(x_N,t_N) \in S_N$. Since X and T are compact, there exist a subsequence $\{(x_{N_k},t_{N_k})\}$ and a point $(\hat{x},\hat{t})\in X\times T$ such that $(x_{N_k},t_{N_k})\rightarrow (\hat{x},\hat{t})$. It follows by (43) and (38) that $(\hat{x},\hat{t})\in {\mathcal {F}}^*$ and $\hat{t}= {\vartheta }^*$. This shows $(\hat{x},\hat{t}) \in S^*$. $\square$

Theorem 2 is instrumental in that it provides a unified quantitative convergence result for the optimal value of ${\hbox {(DRSRP'-N)}}$ in terms of $\mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}^*)$ when ${\mathcal {P}}_N$ is constructed in various ways discussed in Sect. 3. Based on the theorem and some quantitative convergence results about $\mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}^*)$, we can establish confidence intervals for the true optimal value ${\vartheta }^*$ in the following corollary.

Corollary 1

Under the assumptions in Theorem 2, the following assertions hold.

• (i) If ${\mathcal {P}}^*$ comprises the true probability distribution only and ${\mathcal {P}}_N$ is defined by (10), then under conditions of Proposition 3, ${\vartheta }^* \in [{\vartheta }_N-\varTheta , {\vartheta }_N+\varTheta ]$ with probability $1-M\delta$, where

  $$\begin{aligned} \varTheta :=\frac{2 D_XL \kappa }{\eta }[\beta _M+\frac{D}{2} (\max \{2\sqrt{r},r\} +\varDelta (M,N,\delta ))] \end{aligned}$$

  with $\varDelta (M,N,\delta )=\min \left( \frac{M}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) , 4+ \frac{1}{\sqrt{N}}\left( 2+\sqrt{2 \ln \frac{1}{\delta }}\right) \right)$, $\beta _M$ being defined as in (13) and D being the diameter of $\varXi$.

• (ii) If ${\mathcal {P}}^*$ comprises the true probability distribution only and ${\mathcal {P}}_N$ is defined by (26), then under conditions of Proposition 5,

  $$\begin{aligned} {\vartheta }^* \in \left[ {\vartheta }_N-\frac{4 D_XL \kappa r_N(\delta )}{\eta }, {\vartheta }_N+\frac{4 D_XL \kappa r_N(\delta )}{\eta }\right] \end{aligned}$$

  with probability $1-\delta$.

4.1 Extension

Now we turn to extend the convergence result to optimization problems with DRSR constraints:

$$\begin{aligned} \text{(DRSRCP) } \quad \begin{array}{cl} \displaystyle \min _{x \in X} &{}f(x)\\ \text{ s.t. } &{}\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(-c(x,\xi )) \le \gamma , \end{array} \end{aligned}$$

(44)

where decision maker wants to optimize an objective f(x) while requiring the DRSR risk level to be contained under threshold $\gamma$. By replacing ${\mathcal {P}}$ with ${\mathcal {P}}_N$, we may associate (DRSRCP) with

$$\begin{aligned} \text{(DRSRCP-N) } \quad \begin{array}{cl} \displaystyle \min _{x \in X} &{}f(x)\\ \text{ s.t. } &{}\text{ SR }_{l,\lambda }^{{\mathcal {P}}_N}(-c(x,\xi )) \le \gamma . \end{array} \end{aligned}$$

(45)

Tractable reformulation of problem (DRSRCP) or $\text{(DRSRCP-N) }$ may be derived as we did in Sect. 3. In what follows, we establish a theoretical quantitative convergence result for $\text{(DRSRCP-N) }$.

Let $\hat{{\mathcal {F}}}$, $\hat{S}$ and $\hat{{\vartheta }}$ denote respectively the feasible set, the set of the optimal solutions and the optimal value of (DRSRCP). Likewise, we define $\hat{{\mathcal {F}}}_N$, $\hat{S}_N$ and $\hat{{\vartheta }}_N$ for its approximate problem $\text{(DRSRCP-N) }$.

Theorem 3

Let Assumption 1 hold. Suppose that there exists $x_0 \in X$ such that

$$\begin{aligned} \text{ SR }_{l,\lambda }^{{\mathcal {P}}}(-c(x_0,\xi )) < \gamma \end{aligned}$$

and $\mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}})\rightarrow 0$ as $N\rightarrow \infty$. Then the following assertions hold.

• (i) There is a constant $C>0$ such that

  $$\begin{aligned} {\mathbb {H}}(\hat{{\mathcal {F}}}_N,\hat{{\mathcal {F}}}) \le C\mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}}) \end{aligned}$$

  for N sufficiently large.

• (ii) $\displaystyle \lim \nolimits _{N \rightarrow \infty } \hat{{\vartheta }}_N=\hat{{\vartheta }}\,\text{ and }\, \displaystyle \limsup \nolimits _{N\rightarrow \infty } \hat{S}_N =\hat{S}.$

• (iii) If, in addition, f is Lipschitz continuous with modulus $\beta$, then

  $$\begin{aligned} |\hat{{\vartheta }}_N-\hat{{\vartheta }}| \le \beta {\mathbb {H}}(\hat{{\mathcal {F}}}_N,\hat{{\mathcal {F}}}). \end{aligned}$$

  (46)

  Moreover, if $\text{(DRSRCP) }$ satisfies the second order growth condition at the optimal solution set $\hat{S}$, i.e., there exist positive constants $\alpha$ and $\varepsilon$ such that

  $$\begin{aligned} f(x)-\hat{{\vartheta }} \ge \alpha d(x,\hat{S})^2,\, \forall x \in \hat{{\mathcal {F}}} \cap (\hat{S}+\varepsilon \mathbb {B}), \end{aligned}$$

  then

  $$\begin{aligned} \mathbb {D}(\hat{S}_N,\hat{S}) \le \max \left\{ 2C, \sqrt{8C\beta /\alpha }\right\} \sqrt{\mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}})} \end{aligned}$$

  (47)

  when N is sufficiently large.

Proof

• Part (i) can be established through an analogous proof of Theorem 2. We omit the details.

• Part (ii). First we rewrite (DRSRCP) and (DRSRCP-N) as

  $$\begin{aligned} \displaystyle \inf _{x \in \mathrm{I\!R}^n} \tilde{f}(x):=f(x)+\delta _{\hat{{\mathcal {F}}}}(x) \quad \text{ and } \quad \displaystyle \inf _{x \in \mathrm{I\!R}^n} \tilde{f}_N(x):=f(x)+\delta _{\hat{{\mathcal {F}}}_N}(x), \end{aligned}$$

  where $\delta _{\hat{{\mathcal {F}}}}(x)$ is the indicator function of $\hat{{\mathcal {F}}}$, i.e., $\delta _{\hat{{\mathcal {F}}}}(x):= \left\{ \begin{array}{ll} 0, &{}\text{ if }\, x\in \hat{{\mathcal {F}}},\\ +\infty , &{}\text{ if }\, x\notin \hat{{\mathcal {F}}}. \end{array} \right.$ Note that the epigraph of $\delta _{\hat{{\mathcal {F}}}}(\cdot )$ is defined as

  $$\begin{aligned} \text{ epi }\,\delta _{\hat{{\mathcal {F}}}}(\cdot ):=\{(x,\alpha ): \delta _{\hat{{\mathcal {F}}}}(x) \le \alpha \}=\hat{{\mathcal {F}}} \times \mathrm{I\!R}_+. \end{aligned}$$

  The convergence of $\hat{{\mathcal {F}}}_N$ to $\hat{{\mathcal {F}}}$ implies $\displaystyle \lim \nolimits _{N \rightarrow \infty } \text{ epi }\,\delta _{\hat{{\mathcal {F}}}_N}(\cdot )=\text{ epi }\,\delta _{\hat{{\mathcal {F}}}}(\cdot ),$ and through [24, Definition 7.39] that $\delta _{\hat{{\mathcal {F}}}_N}(\cdot )$ epiconverges to $\delta _{\hat{{\mathcal {F}}}}(\cdot )$. Furthermore, it follows from [24, Theorem 7.46] that $\tilde{f}_N$ epiconverges to $\tilde{f}$. Since f is continuous and $\hat{{\mathcal {F}}}$ and $\hat{{\mathcal {F}}}_N$ are compact sets, then any sequence $\{x_N\}$ in $\hat{S}_N$ has a subsequence converging to $\overline{x}$. By [6, Proposition 4.6], $\displaystyle \lim \nolimits _{N \rightarrow \infty } \hat{{\vartheta }}_N=\hat{{\vartheta }}$ and $\overline{x}\in \hat{S}$.

In what follows, we show Part (iii). Let $x_N \in \hat{S}_N$ and $x^* \in \hat{S}$. By the definition of $\mathbb {D}(\hat{{\mathcal {F}}}_N,\hat{{\mathcal {F}}})$, there exists $x_N' \in \hat{{\mathcal {F}}}$ such that $d(x_N,x_N') \le \mathbb {D}(\hat{{\mathcal {F}}}_N,\hat{{\mathcal {F}}})$. Moreover, by the Lipschitz continuity of f, we have

$$\begin{aligned} f(x^*) \le f(x_N')\le & {} f(x_N) +|f(x_N)-f(x_N')| \le f(x_N) +\beta \Vert x_N-x_N'\Vert \\\le & {} f(x_N) +\beta \mathbb {D}(\hat{{\mathcal {F}}}_N,\hat{{\mathcal {F}}}). \end{aligned}$$

Exchanging the role of $x_N$ and $x^*$, we have $f(x_N) \le f(x^*) +\beta \mathbb {D}(\hat{{\mathcal {F}}},\hat{{\mathcal {F}}}_N).$ A combination of the two inequalities yields (46).

Next, we show (47). Let $x_N \in \hat{S}_N$ and $\overline{x} \in \hat{S}$. By the second order growth condition,

$$\begin{aligned} f(x_N)-f(\mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N))= & {} f(x_N)-f(\overline{x})-(f(\mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N))-f(\overline{x}))\\\le & {} f(\mathrm{\Pi }_{\hat{{\mathcal {F}}}_N}(\overline{x}))-f(\overline{x})-\alpha d(\mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N),\hat{S})^2, \end{aligned}$$

where $\mathrm{\Pi }_{\hat{S}}(a)$ denotes the orthogonal projection of vector a on set $\hat{S}$, that is, $\mathrm{\Pi }_{\hat{S}}(a) \in \arg \min _{s\in \hat{S}} \Vert s-a\Vert$. By the Lipschitz continuity of f, the inequality implies

$$\begin{aligned} d(\mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N),\hat{S}) \le \sqrt{(\beta /\alpha )(\Vert \mathrm{\Pi }_{\hat{{\mathcal {F}}}_N}(\overline{x})-\overline{x}\Vert +\Vert \mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N)-x_N\Vert ) }. \end{aligned}$$

Therefore,

$$\begin{aligned} d(x_N,\hat{S})\le & {} \Vert x_N-\mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N)\Vert +d(\mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N),\hat{S})\nonumber \\\le & {} \Vert x_N-\mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N)\Vert + \sqrt{(\beta /\alpha )(\Vert \mathrm{\Pi }_{\hat{{\mathcal {F}}}_N}(\overline{x})-\overline{x}\Vert +\Vert \mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N)-x_N\Vert ) }.\nonumber \\ \end{aligned}$$

(48)

Since $\max \left\{ \max _{x_N\in \hat{S}_N} \Vert x_N-\mathrm{\Pi }_{\hat{{\mathcal {F}}}}(x_N)\Vert , \max _{\overline{x}\in \hat{S}} \Vert \mathrm{\Pi }_{\hat{{\mathcal {F}}}_N}(\overline{x})-\overline{x}\Vert \right\} \le {\mathbb {H}}(\hat{{\mathcal {F}}}_N,\hat{{\mathcal {F}}}),$ we have from inequality (48) and Part (i),

$$\begin{aligned} d(x_N,\hat{S}) \le \max \left\{ C, \sqrt{2C\beta /\alpha }\right\} \left[ \mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}})+\sqrt{\mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}})}\right] . \end{aligned}$$

The last inequality implies (47) in that $x_N$ is arbitrarily chosen from $\hat{S}_N$ and $\mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}})\le \sqrt{\mathbb {H}_K({\mathcal {P}}_N,{\mathcal {P}})}$ when N sufficiently large. $\square$

Analogous to Corollary 1, we can derive confidence intervals and regions for the optimal values with different ${\mathcal {P}}_N$.

5 Application in portfolio optimization

In this section, we apply the (DRSRP) model to decision-making problems in portfolio optimization. Let $\xi _i$ denote the rate of return from investment on stock i and $x_i$ denote the capital invested in the stock i for $i=1,\ldots ,d$. The total return from the investment of the d stocks is $x^T\xi$, where we write $\xi$ for $(\xi _1,\xi _2,\ldots ,\xi _d)^T$ and x for $(x_1,x_2,\ldots ,x_d)^T$. We consider a situation where the investor’s decision on allocation of the capital is based on minimization of the distributionally robust shortfall risk of $x^T\xi$, that is, $\text{ SR }_{l,\lambda }^{{\mathcal {P}}}(x^T\xi )$ for some specified $l,\lambda$ and ${\mathcal {P}}$, that is, the investor finds an optimal decision $x^*$ by solving

$$\begin{aligned} \begin{array}{cl} \displaystyle \min _{x \in X,t \in \mathrm{I\!R}} &{} t\\ \text {s.t.} &{}\displaystyle \sup _{P\in {\mathcal {P}}}{\mathbb {E}}_P[l(-x^T\xi -t)]\le \lambda . \end{array} \end{aligned}$$

(49)

We have undertaken numerical experiments on problem (49) from different perspectives ranging from efficiency of computational schemes as we discussed in Sect. 3, the out-of-sample performance of the optimal portfolio and the growth of the total portfolio value over a specified time horizon using different optimal strategies.

Our main numerical experiments focus on problem (49) with the ambiguity set being defined through the Kantorovich ball. We report the details in Example 1.

Example 1

Let $\xi ^1,\ldots ,\xi ^N$ be iid samples of $\xi$ and $P_N$ be the nominal distribution constructed through the samples, that is, $P_N(\cdot )=\frac{1}{N} \sum _{i=1}^N \mathbb {1}_{\xi ^i}(\cdot ).$ The ambiguity set is defined respectively as

$$\begin{aligned} {\mathcal {P}}_N=\{P \in \mathscr {P} (\mathrm{I\!R}^d): \mathsf {dl}_K(P,P_N) \le r\}. \end{aligned}$$

(50)

To simplify the tests, we consider a specific piecewise affine loss function $l(z)=\max \{0.05 z+1, z+0.1, 4 z+2\}.$ We set $\lambda =1$ and let the total number of stocks d be fixed at 10. We follow Esfahani and Kuhn [8] to generate the iid samples by assuming that the rate of return $\xi _i$ is decomposable into a systematic risk factor $\psi \sim \mathcal{N}(0,2\%)$ common to all stocks and an unsystematic risk factor $\zeta _i \sim \mathcal{N}(i\times 3\%,i\times 2.5\%)$ specific to stock i, that is, $\xi _i=\psi +\zeta _i$, for $i=1,\ldots ,d$.

Based on the discussion in Sect. 3.2, problem (49) can be reformulated through dual formulation as

$$\begin{aligned} \begin{array}{ccl} J_N(r):=&{}\displaystyle \min _{x \in X,t \in \mathrm{I\!R},\eta ,s} &{}t\nonumber \\ &{}\text{ s.t. } &{}\displaystyle \eta r+\frac{1}{N} \sum _{i=1}^N s_i \le 1,\nonumber \\ &{} &{}b_j-a_j t-\langle a_j x,\xi ^i \rangle \le s_i, \; \text{ for }\; i=1,\ldots ,N, j=1,2,3,\nonumber \\ &{} &{}\Vert a_j x\Vert _{*}\le \eta , \; \text{ for }\; j=1,2,3.\nonumber \end{array}\nonumber \\ \end{aligned}$$

(51)

We use $\Vert \cdot \Vert$ to denote 1-norm and thus $\Vert \cdot \Vert _*$ is the $\infty$-norm. Following the terminology of Esfahani and Kuhn [8], we call $J_N(r)$ the certificate.

In the first set of experiments, we investigate the impact of the radius of the Kantorovich ball r on the out-of-sample performance of the optimal portfolio. For any fixed portfolio $x_N(r)$ obtained from problem (51), the out-of-sample performance is defined as $J(x_N(r)):=\text{ SR }^{P^*}_{l,\lambda }(x_N(r)^T\xi ),$ which can be computed from theoretical point of view since the true probability distribution $P^*$ is known by design although in the experiment we will generate a set of validation samples of size $2\times 10^5$ to do the evaluation. Following the same strategy as in [8], we generate the training datasets of cardinality $N \in \{30,300,3000\}$ to solve problem (51) and then use the same validation samples to evaluate $J(x_N(r))$. Each of the experiments is carried out through 200 simulation runs.

Figure 1 depicts the tubes between the 20 and $80\%$ quantiles (shaded areas) and the means (solid lines) of the out-of-sample performance $J(x_N(r))$ as a function of radius r, the dashed lines represent the empirical probability of the event $J(x_N(r)) \le J_N(r)$ with respect to 200 independent runs which is called reliability in Esfahani and Kuhn [8]. It is clear that the reliability is nondecreasing in r and this is because the true probability distribution $P^*$ is located in ${\mathcal {P}}_N$ more likely as r grows and hence the event $J(x_N(r)) \le J_N(r)$ happens more likely. The out-of-sample performance of the portfolio improves (decreases) first and then deteriorates (increases).

In the second set of experiments, we investigate convergence of the out-of-sample performance, the certificate and the reliability of the DRO approach (51) and the SAA approach as the size of sample increases. Note that SAA corresponds to the case when the radius r of the Kantorovich ball is zero. In all of the tests we use cross validation method in [8] to select the Kantorovich radius from the discrete set $\{\{5,6,7,8,9\}\times 10^{-3},\{0,1,2,\ldots ,9\}\times 10^{-2},\{0,1,2,\ldots ,9\}\times 10^{-1}\}$. We have verified that refining or extending the above discrete set has only a marginal impact on the results.

Fig. 1

Out-of-sample performance $J(x_N(r))$ (left axis, solid line and shade area) and reliability Prob$(J(x_N(r)) \le J_N(r))$ (right axis and dashed line) based on 200 independent runs. a$N=30$ training samples, b$N=300$ training samples, c$N=3000$ training samples

Fig. 2

a Out-of-sample performance $J(x_N)$, b certificate $J_N$, and c reliability Prob$(J(x_N) \le J_N)$ for the Kantorovich and SAA solutions of N

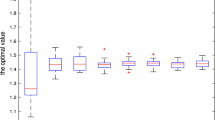
Figure 2a shows the tubes between the 20 and $80\%$ quantiles (shaded areas) and the means (solid lines) of the out-of-sample performance $J(x_N)$ as a function of the sample size N based on 200 independent simulation runs, where $x_N$ is the minimizer of (51) and its SAA counterpart ($r=0$). The constant dashed line represents the optimal value of the SAA problem with $N=10^6$ samples which is regarded as the optimal value of the original problem with the true probability distribution. It is observed that the DRO model (51) outperforms the SAA model in terms of out-of-sample performance. Figure 2b depicts the optimal values of the DRO model and the SAA counterpart, which is the in-sample estimate of the obtained portfolio performance. Both of the approaches display asymptotic consistency, which is consistent with the out-of-sample and in-sample results. Figure 2c describes the empirical probability of the event $J(x_N) \le J_N$ with respect to 200 independent runs, where $x_N$ is the optimal value of the DRO model or SAA model, and $J_N$ are the optimal value of the corresponding problems. It is clear that the performance of the DRO model is better than that of the SAA model.

Example 2

In the last experiment, we evaluate the performance of problem (49) with the ambiguity set being constructed through the KL-divergence ball and the Kantorovich ball, we have also undertaken tests on problem (49) with 10 stocks (Apple Inc., Amazon.com, Inc., Baidu Inc., Costco Wholesale Corporation, DISH Network Corp., eBay Inc., Fox Inc., Alphabet Inc Class A, Marriott International Inc., QUALCOMM Inc.) where their historical data are collected from National Association of Securities Deal Automated Quotations (NASDAQ) index over 4 years (from 3rd May 2011 to 23rd April 2015) with total of 1000 records on the historical stock returns.

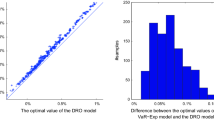
We have carried out out-of-sample tests with a rolling window of 500 days, that is, we use the first 500 data to calculate the optimal portfolio strategy for day 501 and then move on a rolling basis. The radiuses in the two ambiguity sets are selected through the cross validation method. Figure 3 depicts the performance of three models over 500 trading days. It seems that the KL-divergence model and SAA model perform similarly, whereas the Kantorovich model outperforms the both over most of the time period.

Fig. 3

Wealth evolution with the trading times