Abstract
We introduce a concept of dual consistency of systems of linear inequalities with full generality. We show that a cardinality constrained polytope is represented by a certain system of linear inequalities if and only if the systems of linear inequalities associated with the cardinalities are dual consistent. Typical dual consistent systems of inequalities are those which describe polymatroids, generalized polymatroids, and dual greedy polyhedra with certain choice functions. We show that the systems of inequalities for cardinality-constrained ordinary bipartite matching polytopes are not dual consistent in general, and give additional inequalities to make them dual consistent. Moreover, we show that ordinary systems of inequalities for the cardinality-constrained (poly)matroid intersection are not dual consistent, which disproves a conjecture of Maurras, Spiegelberg, and Stephan about a linear representation of the cardinality-constrained polymatroid intersection.


Similar content being viewed by others
Notes
A cardinality constraint in an ordinary sense has the normal vector of all ones, but we consider any non-zero vector \(z_0\) in general.
Note that \(P^{c_1}_{f_1}\) instead of \(P^{c_2}_{f_2}\) works as well.
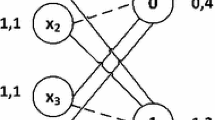
Note that for three sets \(A\), \(B\), and \(C\) with \(A\cap B\ne \emptyset \) and \(B\cap C\ne \emptyset \) we may have \(A\cap C=\emptyset \), which explains the possible non-transitivity. See bipartite matching polytopes discussed in Sect. 4.2 as such an example.
References
Camion, P., Maurras, J.: Polytopes à sommets dans l’ensemble \(\{0,1\}^n\). Cahiers du Centre d’Études de Recherche Opérationnelle 24, 107–120 (1982)
Edmonds, J.: Submodular functions, matroids, and certain polyhedra. In: Guy, R., Hanani, H., Sauer, N., Schönheim, J. (eds.) Proceedings of the Calgary International Conference on Combinatorial Structures and Their Applications. Gordon and Breach, New York, (1970), pp. 69–87; also. In: Combinatorial Optimization-Eureka, You Shrink! (M. Jünger, G. Reinelt and G. Rinaldi, eds., Lecture Notes in Computer Science 2570, Springer, Berlin, 2003), pp. 11–26.
Fujishige, S.: Dual greedy polyhedra, choice functions, and abstract convex geometries. Discrete Optimization 1, 41–49 (2004)
Fujishige, S.: Submodular Functions and Optimization. (Annals of Discrete Mathematics 58), 2nd edn. Elsevier, NY (2005)
Grötschel, M.: Cardinality homogeneous set systems, cycles in matroids, and associated polytopes. In: Grötschel, M. (eds.) The sharpest cut. The impact of Manfred Padberg and his work, MPS-SIAM Series on Optimization vol. 4, pp. 199–216 (2004)
Kaibel, V., Stephan, R.: On cardinality constrained cycle and path polytopes. Mathematical Programming Ser. A 123, 371–394 (2010)
Maurras, J.F.: An example of dual polytopes in the unit hypercube. Annals of Discrete Mathematics 1, 391–392 (1977)
Maurras, J.F., Spiegelberg, I., Stephan, R.: On cardinality constrained polymatroids. Discrete Applied Mathematics (2011). doi:10.1016/j.dam.2011.10.007
Maurras, J.F., Stephan, R.: On the cardinality constrained matroid polytope. Networks 57, 240–246 (2011)
Santos, F.: A counterexample to the Hirsch conjecture. ArXiv:1006.2814v3[math.CO] 8 Nov 2011
Stephan, R.: Cardinality constrained combinatorial optimization: Complexity and polyhedra. Discrete Optimization 7, 99–113 (2010)
Stephan, R., Spiegelberg, I.: On cardinality constrained polymatroids. Electronic Notes in Discrete Mathematics 36, 1017–1024 (2010)
Acknowledgments
The first author’s research was supported by JSPS Grant-in-Aid for Scientific Research (B) 25280004. The second author’s research was done when he was working at the Research Institute for Discrete Mathematics, University of Bonn. The present research was partly supported due to the “General Agreement for Cooperation between Hausdorff Center for Mathematics, University of Bonn and Research Institute for Mathematical Sciences, Kyoto University”. The authors thank the two anonymous referees for their useful comments that improved the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Fujishige, S., Maßberg, J. Dual consistent systems of linear inequalities and cardinality constrained polytopes. Math. Program. 150, 35–48 (2015). https://doi.org/10.1007/s10107-014-0748-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-014-0748-2