A stability analysis of landslides based on random fields, part II: base circle slope

Abstract

In this paper, the stability of base circle slopes is analyzed based on the theory of random fields. The closed-form solution of the safety factor and the failure probability of base circle slopes are obtained using the integration method. The effects of the spatial variation of the mechanical parameters of soils on the stability of base circle slopes are investigated. The mean values of the safety factor and the failure probability of base circle slopes are determined. The effects of spatial correlation length on the failure probability of base circle slopes are studied. The results show that for homogeneous slopes, the accuracy of the vertical integration model is greater than that of the horizontal integration model. For layered slopes, the effectiveness of the horizontal integration method is validated by a Monte Carlo simulation. Therefore, the horizontal integration model is more suitable for the layered slopes than the vertical integration model.

Appendices

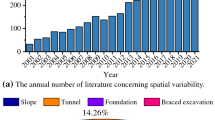
Appendix 1

Here, to consider the possible correlation between cohesion and the friction coefficient, a random field correlation function is written as

$$ E\left[ \tan \varphi (x) \tan \varphi \left({x}^{\hbox{'}}\right)\right]={\mu}_{\tan \varphi}^2+{C}_{\tan \varphi}\left( x-{x}^{\hbox{'}}\right) $$

(34)

$$ E\left[ c(x) c\left({x}^{\hbox{'}}\right)\right]={\mu}_c^2+{C}_c\left( x-{x}^{\hbox{'}}\right) $$

(35)

$$ E\left[ \tan \varphi (x) c\left({x}^{\hbox{'}}\right)\right]={\mu}_{\tan \varphi}{\mu}_c+{C}_{\mathrm{c}- \tan \varphi}\left( x-{x}^{\hbox{'}}\right) $$

(36)

The autocorrelation of the respective random fields can be expressed by Eq. (34) and (35). The cross-correlation between the two random fields can be expressed by Eq. (36). It is assumed that the corresponding covariance function is a general Markov form (Fenton and Griffiths 2008; Huang et al. 2016; Gravanis et al. 2014).

$$ {C}_{\tan \varphi}(x)={\sigma}_{\tan \varphi}^2 \exp \left[-\frac{2\left| x\right|}{\theta_{\tan \varphi}}\right] $$

(37)

$$ {C}_c(x)={\sigma}_c^2 \exp \left[-\frac{2\left| x\right|}{\theta_c}\right] $$

(38)

$$ {C}_{\mathrm{c}- \tan \varphi}(x)={\rho}_{\mathrm{c}- \tan \varphi}{\sigma}_c{\sigma}_{\tan \varphi} \exp \left[-\frac{2\left| x\right|}{\theta_{\mathrm{c}- \tan \varphi}}\right] $$

(39)

where σ_tanφ and σ_c are respectively the point variances of the friction coefficient and cohesion, and θ_tanφ and θ_c are the respective correlation lengths. The parameter ρ_{c − tan φ} is the correlation coefficient, and θ_{c − tan φ} is the cross-correlation length. Then, the variance of the safety factor F of the base circle slope based on the horizontal integration model can be explicitly expressed as

$$ \begin{array}{l} E\left[{F}^2\right]=\frac{4{r}^2}{{Q_1}^2}\left\{{U}_1^2{\mu}_{1, \tan \varphi}^2+{U}_2^2{\mu}_{2, \tan \varphi}^2+{U}_3^2{\mu}_{3, \tan \varphi}^2+2{\mathrm{U}}_1{U}_2{\mu}_{1, \tan \varphi}{\mu}_{2, \tan \varphi}+2{\mathrm{U}}_1{U}_3{\mu}_{1, \tan \varphi}{\mu}_{3, \tan \varphi}\right.\hfill \\ {}\kern3em +2{\mathrm{U}}_2{U}_3{\mu}_{2, \tan \varphi}{\mu}_{3, \tan \varphi}+{\sigma}_{1, \tan \varphi}^2{\int}_{\theta_E}^0 d\theta {\int}_{\theta_E}^0{d\theta}^{\hbox{'}}{t}_1\left(\theta \right){t}_1\left({\theta}^{\hbox{'}}\right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\tan \varphi}}\right]\hfill \\ {}\kern3em +{\sigma}_{2, \tan \varphi}^2{\int}_0^{\theta_D} d\theta {\int}_0^{\theta_D}{d\theta}^{\hbox{'}}{t}_2\left(\theta \right){t}_2\left({\theta}^{\hbox{'}}\right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\tan \varphi}}\right]\hfill \\ {}\kern3em +\left.{\sigma}_{3, \tan \varphi}^2{\int}_{\theta_D}^{\theta_B} d\theta {\int}_{\theta_D}^{\theta_B}{d\theta}^{\hbox{'}}{t}_3\left(\theta \right){t}_3\left({\theta}^{\hbox{'}}\right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\tan \varphi}}\right]\right\}\hfill \\ {}\kern3em +\frac{4{r}^2}{\gamma^2{Q_1}^2}\left\{{\mu}_c^2{\left({\theta}_B-{\theta}_E\right)}^2+{\sigma}_c^2{\int}_{\theta_E}^{\theta_B} d\theta {\int}_{\theta_E}^{\theta_B}{d\theta}^{\hbox{'}} \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_c}\right]\right\}\hfill \\ {}\kern3em +\frac{8{r}^2}{\gamma {Q_1}^2}\left\{{\mu}_c\left({\mathrm{U}}_1{\mu}_{1, \tan \varphi}+{\mathrm{U}}_2{\mu}_{2, \tan \varphi}+{U}_3{\mu}_{3, \tan \varphi}\right)\left({\theta}_B-{\theta}_E\right)\right.\hfill \\ {}\kern3em +{\rho}_{c- \tan \varphi}{\sigma}_c{\sigma}_{1, \tan \varphi}{\int}_{\theta_E}^0 d\theta {\int}_{\theta_E}^0{d\theta}^{\hbox{'}}{t}_1\left(\theta \right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\mathrm{c}- \tan \varphi}}\right]\hfill \\ {}\kern3.25em +{\rho}_{c- \tan \varphi}{\sigma}_c{\sigma}_{2, \tan \varphi}{\int}_0^{\theta_D} d\theta {\int}_0^{\theta_D}{d\theta}^{\hbox{'}}{t}_2\left(\theta \right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\mathrm{c}- \tan \varphi}}\right]\hfill \\ {}\kern3em + \left.{\rho}_{c- \tan \varphi}{\sigma}_c{\sigma}_{3, \tan \varphi}{\int}_{\theta_D}^{\theta_B} d\theta {\int}_{\theta_D}^{\theta_B}{d\theta}^{\hbox{'}}{t}_3\left(\theta \right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\mathrm{c}- \tan \varphi}}\right]\right\}\hfill \end{array} $$

(40)

The variance of the safety factor F of the base circle slope based on the horizontal integration model can be obtained by the following expression:

$$ {s}_F^2\equiv Var\left[ F\right]=\frac{4{r}^2}{{Q_1}^2}{s}_{\tan \varphi}^2+\frac{4{r}^2}{\gamma^2{Q_1}^2}{s}_c^2+\frac{8{r}^2}{\gamma {Q_1}^2}{s}_{c- \tan \varphi}^2 $$

(41)

where

$$ \begin{array}{l}{s}_{\tan \varphi}^2={\sigma}_{1, \tan \varphi}^2\left[{T}_1\left({\theta}_E\right){T}_2\left({\theta}_E\right)+\frac{4 kr}{\left({k}^2+1\right)\left({k}^2+9\right)}{T}_1\left({\theta}_E\right){e}^{k{\theta}_E}-\frac{4{k}^2{r}^2}{{\left({k}^2+1\right)}^2{\left({k}^2+9\right)}^2}+{R}_1{I}_1+{R}_2{I}_2\right]\hfill \\ {}\kern2em +{\sigma}_{2, \tan \varphi}^2\left[{T}_1\left({\theta}_D\right){T}_2\left({\theta}_D\right)-\frac{4 kr}{\left({k}^2+1\right)\left({k}^2+9\right)}{T}_2\left({\theta}_D\right){e}^{- k{\theta}_D}-\frac{4{k}^2{r}^2}{{\left({k}^2+1\right)}^2{\left({k}^2+9\right)}^2}+{R}_3{I}_3+{R}_4{I}_4\right]\hfill \\ {}\kern2.5em +{\sigma}_{3, \tan \varphi}^2\left[{T}_3\left({\theta}_D\right){T}_4\left({\theta}_D\right)+{T}_3\left({\theta}_B\right){T}_4\left({\theta}_B\right)-2{T}_3\left({\theta}_D\right){T}_4\left({\theta}_B\right){e}^{k\left({\theta}_D-{\theta}_B\right)}\right.\hfill \\ {}\left.\kern2.5em +{R}_5{I}_5+{R}_6{I}_6+{R}_7{I}_7+{R}_8{I}_8+{R}_9{I}_9+{R}_{10}{I}_{10}+{R}_{11}{I}_{11}+{R}_{12}{I}_{12}\right]\hfill \end{array} $$

(42)

$$ {s}_c^2={\sigma}_c^2\frac{2}{k_1^2}\left[{e}^{k_1\left({\theta}_E-{\theta}_B\right)}+{k}_1\left({\theta}_B-{\theta}_E\right)-1\right] $$

(43)

$$ \begin{array}{l}{s}_{c- \tan \varphi}^2={\rho}_{\mathrm{c}- \tan \varphi}{\sigma}_c{\sigma}_{1, \tan \varphi}\frac{1}{k_2}\left[2{U}_1+{T}_6\left({\theta}_E\right)+\frac{2{k}_2 r}{\left({k}_2^2+1\right)\left({k}_2^2+9\right)}\left({e}^{k_2{\theta}_E}-1\right)+{T}_5\left({\theta}_E\right){e}^{k_2{\theta}_E}\right]\hfill \\ {}\kern2em +{\rho}_{\mathrm{c}- \tan \varphi}{\sigma}_c{\sigma}_{2, \tan \varphi}\frac{1}{k_2}\left[2{U}_2-{T}_5\left({\theta}_D\right)+\frac{2{k}_2 r}{\left({k}_2^2+1\right)\left({k}_2^2+9\right)}\left({e}^{-{k}_2{\theta}_D}-1\right)-{T}_6\left({\theta}_D\right){e}^{-{k}_2{\theta}_D}\right]\hfill \\ {}\kern2.5em +{\rho}_{\mathrm{c}- \tan \varphi}{\sigma}_c{\sigma}_{3, \tan \varphi}\frac{1}{k_2}\left[2{U}_3+{T}_8\left({\theta}_D\right)-{T}_7\left({\theta}_B\right)+\left({T}_7\left({\theta}_D\right)-{T}_8\left({\theta}_B\right)\right){e}^{k_2\left({\theta}_D-{\theta}_B\right)}\right]\hfill \end{array} $$

(44)

$$ {T}_1\left(\theta \right)=\frac{r}{k^2+9}\times \left[ k{ \sin}^2\theta \cos \theta -3 \sin \theta { \cos}^2\theta +\frac{\left({k}^2+3\right) \sin \theta +2 k \cos \theta}{k^2+1}\right] $$

(45)

$$ {T}_2\left(\theta \right)=\frac{r}{k^2+9}\times \left[- k{ \sin}^2\theta \cos \theta -3 \sin \theta { \cos}^2\theta +\frac{\left({k}^2+3\right) \sin \theta -2 k \cos \theta}{k^2+1}\right] $$

(46)

$$ \begin{array}{l}{T}_3\left(\theta \right)=\frac{a- b \cot \beta}{k^2+4}\left( k \sin \theta \cos \theta -{ \cos}^2\theta +{ \sin}^2\theta \right)\hfill \\ {}\kern2em +\frac{r}{k^2+9}\times \left[\left( k \cot \beta -3\right) \sin \theta { \cos}^2\theta \left.+\left( k+3 \cot \beta \right){ \sin}^2\theta \cos \theta \right]\right.\hfill \\ {}\kern2em +\frac{r\left({k}^2+2\mathrm{k} \cot \beta +3\right) \sin \theta - r\left({k}^2 \cot \beta -2\mathrm{k}+3 \cot \beta \right) \cos \theta}{\left({k}^2+1\right)\left({k}^2+9\right)}\hfill \end{array} $$

(47)

$$ \begin{array}{l}{T}_4\left(\theta \right)=\frac{b \cot \beta - a}{k^2+4}\left( k \sin \theta \cos \theta +{ \cos}^2\theta -{ \sin}^2\theta \right)\hfill \\ {}\kern2em +\frac{r}{k^2+9}\times \left[-\left( k \cot \beta +3\right) \sin \theta { \cos}^2\theta \left.-\left( k-3 \cot \beta \right){ \sin}^2\theta \cos \theta \right]\right.\hfill \\ {}\kern2em +\frac{r\left({k}^2-2\mathrm{k} \cot \beta +3\right) \sin \theta - r\left({k}^2 \cot \beta +2\mathrm{k}+3 \cot \beta \right) \cos \theta}{\left({k}^2+1\right)\left({k}^2+9\right)}\hfill \end{array} $$

(48)

$$ {T}_5\left(\theta \right)=\frac{r}{{k_2}^2+9}\left[{k}_2{ \sin}^2\theta \cos \theta -3 \sin \theta { \cos}^2\theta \left.+\frac{\left({k_2}^2+3\right) \sin \theta +2{\mathrm{k}}_2 \cos \theta}{{k_2}^2+1}\right]\right. $$

(49)

$$ {T}_6\left(\theta \right)=\frac{r}{{k_2}^2+9}\left[-{k}_2{ \sin}^2\theta \cos \theta -3 \sin \theta { \cos}^2\theta \left.+\frac{\left({k_2}^2+3\right) \sin \theta -2{\mathrm{k}}_2 \cos \theta}{{k_2}^2+1}\right]\right. $$

(50)

$$ \begin{array}{l}{T}_7\left(\theta \right)=\frac{a- b \cot \beta}{{k_2}^2+4}\left({k}_2 \sin \theta \cos \theta -{ \cos}^2\theta +{ \sin}^2\theta \right)\hfill \\ {}\kern2em +\frac{r}{{k_2}^2+9}\left[\left({k}_2 \cot \beta -3\right) \sin \theta { \cos}^2\theta \left.+\left({k}_2+3 \cot \beta \right){ \sin}^2\theta \cos \theta \right]\right.\hfill \\ {}\kern2em +\frac{r\left({k_2}^2+2{\mathrm{k}}_2 \cot \beta +3\right) \sin \theta - r\left({k_2}^2 \cot \beta -2{\mathrm{k}}_2+3 \cot \beta \right) \cos \theta}{\left({k_2}^2+1\right)\left({k_2}^2+9\right)}\hfill \end{array} $$

(51)

$$ \begin{array}{l}{T}_8\left(\theta \right)=\frac{b \cot \beta - a}{{k_2}^2+4}\left({k}_2 \sin \theta \cos \theta +{ \cos}^2\theta -{ \sin}^2\theta \right)\hfill \\ {}\kern2em +\frac{r}{{k_2}^2+9}\left[-\left({k}_2 \cot \beta +3\right) \sin \theta { \cos}^2\theta \left.-\left({k}_2-3 \cot \beta \right){ \sin}^2\theta \cos \theta \right]\right.\hfill \\ {}\kern2em +\frac{r\left({k_2}^2-2{\mathrm{k}}_2 \cot \beta +3\right) \sin \theta - r\left({k_2}^2 \cot \beta +2{\mathrm{k}}_2+3 \cot \beta \right) \cos \theta}{\left({k_2}^2+1\right)\left({k_2}^2+9\right)}\hfill \end{array} $$

(52)

$$ \left\{\begin{array}{l}{R}_1={R}_3=\frac{{ k r}^2}{8\left({k}^2+9\right)}\kern1em \\ {}{R}_2={R}_4=\frac{{ k r}^2}{2\left({k}^2+1\right)\left({k}^2+9\right)}\kern0.75em \end{array}\right. $$

(53)

$$ \left\{\begin{array}{l}\kern0.5em {I}_1=-{\theta}_E+\frac{1}{4} \sin 2{\theta}_E+\frac{1}{4} \sin 4{\theta}_E-\frac{1}{12} \sin 6{\theta}_E\\ {}{I}_2=-{\theta}_E+\frac{1}{4} \sin 4{\theta}_E\kern0.75em \end{array}\right. $$

(54)

$$ \left\{\begin{array}{l}\kern0.5em {I}_3={\theta}_D-\frac{1}{4} \sin 2{\theta}_D-\frac{1}{4} \sin 4{\theta}_D+\frac{1}{12} \sin 6{\theta}_D\\ {}{I}_4={\theta}_D-\frac{1}{4} \sin 4{\theta}_D\kern0.75em \end{array}\right. $$

(55)

$$ \left\{\begin{array}{l}{R}_5=-\frac{4 kr\left( a- b \cot \beta \right)}{3\left({k}^2+1\right)\left({k}^2+9\right)},\kern0.5em {R}_6=\frac{4 kr \cot \beta \left( a- b \cot \beta \right)}{3\left({k}^2+1\right)\left({k}^2+9\right)}\ \\ {}{R}_7=\frac{{k r}^2 \cot \beta}{\left({k}^2+1\right)\left({k}^2+9\right)}\kern0.75em \\ {}{R}_8=\frac{k{\left( a- b \cot \beta \right)}^2}{4\left({k}^2+4\right)}+\frac{{k r}^2\left({k}^2+5\right)\left(1+{ \cot}^2\beta \right)}{8\left({k}^2+1\right)\left({k}^2+9\right)}\kern0.5em \\ {}{R}_9=2 kr \cot \beta \left( a- b \cot \beta \right)\left(\frac{1}{k^2+4}+\frac{1}{k^2+9}\right)\\ {}{R}_{10}=2 kr\left( a- b \cot \beta \right)\left(\frac{1}{k^2+4}+\frac{1}{k^2+9}\right)\kern0.5em \\ {}{R}_{11}=\frac{{k r}^2 \cot \beta}{k^2+9},{R}_{12}=\frac{{k r}^2\left({ \cot}^2\beta -1\right)}{32\left({k}^2+9\right)}\end{array}\right. $$

(56)

$$ \left\{\begin{array}{l}{I}_5=\left({ \cos}^3{\theta}_B-{ \cos}^3{\theta}_D\right),\kern0.5em {I}_6=\left({ \sin}^3{\theta}_B-{ \sin}^3{\theta}_D\right)\kern0.75em \\ {}{I}_7=\left({ \sin}^4{\theta}_B-{ \sin}^4{\theta}_D\right)-\left({ \cos}^4{\theta}_B-{ \cos}^4{\theta}_D\right)\kern0.75em \\ {}{I}_8=\left({\theta}_B-{\theta}_D\right)-\frac{1}{4}\left( \sin 4{\theta}_B- \sin 4{\theta}_D\right)\kern0.75em \\ {}{I}_9=\frac{1}{3}\left({ \sin}^3{\theta}_B-{ \sin}^3{\theta}_D\right)-\frac{1}{5}\left({ \sin}^5{\theta}_B-{ \sin}^5{\theta}_D\right)\\ {}{I}_{10}=\frac{1}{5}\left({ \cos}^5{\theta}_B-{ \cos}^5{\theta}_D\right)-\frac{1}{3}\left({ \cos}^3{\theta}_B-{ \cos}^3{\theta}_D\right)\kern0.5em \\ {}{I}_{11}=\left({ \sin}^4{\theta}_B-{ \sin}^4{\theta}_D\right)-\frac{2}{3}\left({ \sin}^6{\theta}_B-{ \sin}^6{\theta}_D\right)\\ {}{I}_{12}=\left( \sin 2{\theta}_B- \sin 2{\theta}_D\right)-\frac{1}{3}\left( \sin 6{\theta}_B- \sin 6{\theta}_D\right)\end{array}\right. $$

(57)

$$ k=\frac{2 r}{\theta_{\tan \varphi}} $$

(58)

$$ {k}_1=\frac{2 r}{\theta_c} $$

(59)

$$ {k}_2=\frac{2 r}{\theta_{c- \tan \varphi}} $$

(60)

Appendix 2

The variance of the safety factor F of the base circle slope based on the vertical integration model can be explicitly expressed.

$$ \begin{array}{l} E\left[{F}^2\right]=\frac{1}{{Q_2}^2}\left\{{\mathrm{U}}_4^2{\mu}_{4, \tan \varphi}^2+{\mathrm{U}}_5^2{\mu}_{5, \tan \varphi}^2+{\mathrm{U}}_6^2{\mu}_{6, \tan \varphi}^2+2{U}_4{U}_5{\mu}_{4, \tan \varphi}{\mu}_{5, \tan \varphi}+2{U}_4{U}_6{\mu}_{4, \tan \varphi}{\mu}_{6, \tan \varphi}+2{U}_5{U}_6\right.\\ {}\kern2.75em \times {\mu}_{5, \tan \varphi}{\mu}_{6, \tan \varphi}+{\sigma}_{4, \tan \varphi}^2{\int}_{\theta_E}^{\theta_I} d\theta {\int}_{\theta_E}^{\theta_I}{d\theta}^{\hbox{'}}\ {\mathrm{t}}_4\left(\theta \right){\mathrm{t}}_4\left({\theta}^{\hbox{'}}\right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\tan \varphi}}\right]+{\sigma}_{5, \tan \varphi}^2{\int}_{\theta_I}^{\theta_H} d\theta {\int}_{\theta_I}^{\theta_H}{d\theta}^{\hbox{'}}\ \\ {}\kern3em \left.{\mathrm{t}}_5\left(\theta \right){\mathrm{t}}_5\left({\theta}^{\hbox{'}}\right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\tan \varphi}}\right]+{\sigma}_{6, \tan \varphi}^2{\int}_{\theta_H}^{\theta_B} d\theta {\int}_{\theta_H}^{\theta_B}{d\theta}^{\hbox{'}}\ {\mathrm{t}}_6\left(\theta \right){\mathrm{t}}_6\left({\theta}^{\hbox{'}}\right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\tan \varphi}}\right]\right\}\\ {}\kern3em +\frac{1}{\gamma^2{Q_2}^2}\left\{{\mu}_c^2{\left({\theta}_B-{\theta}_E\right)}^2+{\sigma}_c^2{\int}_{\theta_E}^{\theta_B} d\theta {\int}_{\theta_E}^{\theta_B}{d\theta}^{\hbox{'}}\ \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_c}\right]\right\}\\ {}\kern2.75em +\frac{2}{\gamma {Q_2}^2}\left\{{\mu}_c\left({U}_4{\mu}_{4, \tan \varphi}+{U}_5{\mu}_{5, \tan \varphi}+{U}_6{\mu}_{6, \tan \varphi}\right)\left({\theta}_B-{\theta}_E\right)+{\rho}_{c- \tan \varphi}{\sigma}_c{\sigma}_{4, \tan \varphi}\right.\\ {}\kern2.75em {\int}_{\theta_E}^{\theta_I} d\theta {\int}_{\theta_E}^{\theta_I}{d\theta}^{\hbox{'}}\ {\mathrm{t}}_4\left(\theta \right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\mathrm{c}- \tan \varphi}}\right]+{\rho}_{c- \tan \varphi}{\sigma}_c{\sigma}_{5, \tan \varphi}{\int}_{\theta_I}^{\theta_H} d\theta {\int}_{\theta_I}^{\theta_H}{d\theta}^{\hbox{'}}\ {\mathrm{t}}_5\left(\theta \right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\mathrm{c}- \tan \varphi}}\right]\\ {}\kern2.5em +{\rho}_{c- \tan \varphi}{\sigma}_c{\sigma}_{6, \tan \varphi}{\int}_{\theta_H}^{\theta_B} d\theta {\int}_{\theta_H}^{\theta_B}{d\theta}^{\hbox{'}}\ {\mathrm{t}}_6\left(\theta \right) \exp \left[-\frac{2 r\left|\theta -{\theta}^{\hbox{'}}\right|}{\theta_{\mathrm{c}- \tan \varphi}}\right]\\ {}\kern2.75em \end{array} $$

(61)

The variance of the safety factor F of the base circle slope based on the vertical integration model can be written in the following form

$$ {S}_F^2\equiv Var\left[ F\right]=\frac{1}{{Q_2}^2}{S}_{\tan \varphi}^2+\frac{1}{\gamma^2{Q_2}^2}{S}_c^2+\frac{2}{\gamma {Q_2}^2}{S}_{\mathrm{c}- \tan \varphi}^2 $$

(62)

where

$$ \begin{array}{l}{S}_{\tan \varphi}^2={\sigma}_{4, \tan \varphi}^2\left[{T}_9\left({\theta}_E\right)\ {T}_{10}\left({\theta}_E\right)+{T}_9\left({\theta}_I\right)\ {T}_{10}\left({\theta}_I\right)-2{T}_9\left({\theta}_E\right)\ {T}_{10}\left({\theta}_I\right){e}^{k\left({\theta}_E-{\theta}_I\right)}\right.\hfill \\ {}\left.\kern2em +{R}_{13}{I}_{13}+{R}_{14}{I}_{14}+{R}_{15}{I}_{15}+{R}_{16}{I}_{16}+{R}_{17}{I}_{17}+{R}_{18}{I}_{18}+{R}_{19}{I}_{19}\right]\hfill \\ {}\kern2em +{\sigma}_{5, \tan \varphi}^2\left[{T}_{11}\left({\theta}_I\right)\ {T}_{12}\left({\theta}_I\right)+{T}_{11}\left({\theta}_H\right)\ {T}_{12}\left({\theta}_H\right)-2{T}_{11}\left({\theta}_I\right)\ {T}_{12}\left({\theta}_H\right){e}^{k\left({\theta}_I-{\theta}_H\right)}+{R}_{20}{I}_{20}+{R}_{21}{I}_{21}+{R}_{22}{I}_{22}\right.\hfill \\ {}\left.\kern2.5em +{R}_{23}{I}_{23}+{R}_{24}{I}_{24}+{R}_{25}{I}_{25}+{R}_{26}{I}_{26}+{R}_{27}{I}_{27}+{R}_{28}{I}_{28}+{R}_{29}{I}_{29}+{R}_{30}{I}_{30}+{R}_{31}{I}_{31}+{R}_{32}{I}_{32}\right]\hfill \\ {}\kern2em +{\sigma}_{6, \tan \varphi}^2\left[{T}_{13}\left({\theta}_H\right)\ {T}_{14}\left({\theta}_H\right)+{T}_{13}\left({\theta}_B\right)\ {T}_{14}\left({\theta}_B\right)-2{T}_{13}\left({\theta}_H\right)\ {T}_{14}\left({\theta}_B\right){e}^{k\left({\theta}_H-{\theta}_B\right)}\right.\hfill \\ {}\left.\kern2em +{R}_{33}{I}_{33}+{R}_{34}{I}_{34}+{R}_{35}{I}_{35}+{R}_{36}{I}_{36}+{R}_{37}{I}_{37}+{R}_{38}{I}_{38}+{R}_{39}{I}_{39}\right]\hfill \end{array} $$

(63)

$$ {S}_c^2={\sigma}_c^2\frac{2}{k_1^2}\left[{e}^{k_1\left({\theta}_E-{\theta}_B\right)}+{k}_1\left({\theta}_B-{\theta}_E\right)-1\right] $$

(64)

$$ \begin{array}{l}{S}_{c- \tan \varphi}^2={\rho}_{\mathrm{c}- \tan \varphi}{\sigma}_c{\sigma}_{4, \tan \varphi}\frac{1}{k_2}\left[2{U}_4-{T}_{15}\left({\theta}_I\right)+{T}_{16}\left({\theta}_E\right)+\left({T}_{15}\left({\theta}_E\right)-{T}_{16}\left({\theta}_I\right)\right){e}^{k_2\left({\theta}_E-{\theta}_I\right)}\right]\hfill \\ {}\kern2.5em +{\rho}_{\mathrm{c}- \tan \varphi}{\sigma}_c{\sigma}_{5, \tan \varphi}\frac{1}{k_2}\left[2{U}_5-{T}_{17}\left({\theta}_H\right)+{T}_{18}\left({\theta}_I\right)+\left({T}_{17}\left({\theta}_I\right)-{T}_{18}\left({\theta}_H\right)\right){e}^{k_2\left({\theta}_I-{\theta}_H\right)}\right]\hfill \\ {}\kern2.5em +{\rho}_{\mathrm{c}- \tan \varphi}{\sigma}_c{\sigma}_{6, \tan \varphi}\frac{1}{k_2}\left[2{U}_6-{T}_{19}\left({\theta}_B\right)+{T}_{20}\left({\theta}_H\right)+\left({T}_{19}\left({\theta}_H\right)-{T}_{20}\left({\theta}_B\right)\right){e}^{k_2\left({\theta}_H-{\theta}_B\right)}\right]\hfill \end{array} $$

(65)

$$ \begin{array}{l}{T}_9\left(\theta \right)=\frac{- b}{k}\left[{ \cos}^2\theta +\frac{2\left( k \sin \theta \cos \theta -{ \cos}^2\theta +{ \sin}^2\theta \right)}{k^2+4}\right]+\frac{r}{k}{ \cos}^3\theta \hfill \\ {}\kern2.5em +\frac{3 r}{k\left({k}^2+9\right)}\left[ k \sin \theta { \cos}^2\theta +3{ \sin}^2\theta \cos \theta +\frac{2 k \sin \theta -\left({k}^2+3\right) \cos \theta}{k^2+1}\right]\hfill \end{array} $$

(66)

$$ \begin{array}{l}{T}_{10}\left(\theta \right)=\frac{b}{k}\left[{ \cos}^2\theta -\frac{2\left( k \sin \theta \cos \theta +{ \cos}^2\theta -{ \sin}^2\theta \right)}{k^2+4}\right]-\frac{r}{k}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{3 r}{k\left({k}^2+9\right)}\left[ k \sin \theta { \cos}^2\theta -3{ \sin}^2\theta \cos \theta +\frac{2 k \sin \theta +\left({k}^2+3\right) \cos \theta}{k^2+1}\right]\hfill \end{array} $$

(67)

$$ \begin{array}{l}{T}_{11}\left(\theta \right)=\frac{a \tan \beta - b}{k}\left[{ \cos}^2\theta +\frac{2\left( k \sin \theta \cos \theta -{ \cos}^2\theta +{ \sin}^2\theta \right)}{k^2+4}\right]+\frac{r}{k}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{r}{k^2+9}\left(\frac{3}{k}+ \tan \beta \right)\left[ k \sin \theta { \cos}^2\theta +3{ \sin}^2\theta \cos \theta +\frac{2 k \sin \theta -\left({k}^2+3\right) \cos \theta}{k^2+1}\right]\hfill \end{array} $$

(68)

$$ \begin{array}{l}{T}_{12}\left(\theta \right)=\frac{b- a \tan \beta}{k}\left[{ \cos}^2\theta -\frac{2\left( k \sin \theta \cos \theta +{ \cos}^2\theta -{ \sin}^2\theta \right)}{k^2+4}\right]-\frac{r}{k}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{r}{k^2+9}\left(\frac{3}{k}- \tan \beta \right)\left[ k \sin \theta { \cos}^2\theta -3{ \sin}^2\theta \cos \theta +\frac{2 k \sin \theta +\left({k}^2+3\right) \cos \theta}{k^2+1}\right]\hfill \end{array} $$

(69)

$$ \begin{array}{l}{T}_{13}\left(\theta \right)=\frac{h- b}{k}\left[{ \cos}^2\theta +\frac{2\left( k \sin \theta \cos \theta -{ \cos}^2\theta +{ \sin}^2\theta \right)}{k^2+4}\right]+\frac{r}{k}{ \cos}^3\theta \hfill \\ {}\kern2em +\frac{3 r}{k\left({k}^2+9\right)}\left[ k \sin \theta { \cos}^2\theta +3{ \sin}^2\theta \cos \theta +\frac{2 k \sin \theta -\left({k}^2+3\right) \cos \theta}{k^2+1}\right]\hfill \end{array} $$

(70)

$$ \begin{array}{l}{T}_{14}\left(\theta \right)=\frac{b- h}{k}\left[{ \cos}^2\theta -\frac{2\left( k \sin \theta \cos \theta +{ \cos}^2\theta -{ \sin}^2\theta \right)}{k^2+4}\right]-\frac{r}{k}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{3 r}{k\left({k}^2+9\right)}\left[ k \sin \theta { \cos}^2\theta -3{ \sin}^2\theta \cos \theta +\frac{2 k \sin \theta +\left({k}^2+3\right) \cos \theta}{k^2+1}\right]\hfill \end{array} $$

(71)

$$ \begin{array}{l}{T}_{15}\left(\theta \right)=\frac{- b}{k_2}\left[{ \cos}^2\theta +\frac{2\left({k}_2 \sin \theta \cos \theta -{ \cos}^2\theta +{ \sin}^2\theta \right)}{{k_2}^2+4}\right]+\frac{r}{k_2}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{3 r}{k_2\left({k_2}^2+9\right)}\left[{k}_2 \sin \theta { \cos}^2\theta +3{ \sin}^2\theta \cos \theta +\frac{2{k}_2 \sin \theta -\left({k_2}^2+3\right) \cos \theta}{{k_2}^2+1}\right]\hfill \end{array} $$

(72)

$$ \begin{array}{l}{T}_{16}\left(\theta \right)=\frac{b}{k_2}\left[{ \cos}^2\theta -\frac{2\left({k}_2 \sin \theta \cos \theta +{ \cos}^2\theta -{ \sin}^2\theta \right)}{{k_2}^2+4}\right]-\frac{r}{k_2}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{3 r}{k_2\left({k_2}^2+9\right)}\left[{k}_2 \sin \theta { \cos}^2\theta -3{ \sin}^2\theta \cos \theta +\frac{2{k}_2 \sin \theta +\left({k_2}^2+3\right) \cos \theta}{{k_2}^2+1}\right]\hfill \end{array} $$

(73)

$$ \begin{array}{l}{T}_{17}\left(\theta \right)=\frac{a \tan \beta - b}{k_2}\left[{ \cos}^2\theta +\frac{2\left({k}_2 \sin \theta \cos \theta -{ \cos}^2\theta +{ \sin}^2\theta \right)}{{k_2}^2+4}\right]+\frac{r}{k_2}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{r}{{k_2}^2+9}\left(\frac{3}{k_2}+ \tan \beta \right)\left[{k}_2 \sin \theta { \cos}^2\theta +3{ \sin}^2\theta \cos \theta +\frac{2{k}_2 \sin \theta -\left({k_2}^2+3\right) \cos \theta}{{k_2}^2+1}\right]\hfill \end{array} $$

(74)

$$ \begin{array}{l}{T}_{18}\left(\theta \right)=\frac{b- a \tan \beta}{k_2}\left[{ \cos}^2\theta -\frac{2\left({k}_2 \sin \theta \cos \theta +{ \cos}^2\theta -{ \sin}^2\theta \right)}{{k_2}^2+4}\right]-\frac{r}{k_2}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{r}{{k_2}^2+9}\left(\frac{3}{k_2}- \tan \beta \right)\left[{k}_2 \sin \theta { \cos}^2\theta -3{ \sin}^2\theta \cos \theta +\frac{2{k}_2 \sin \theta +\left({k_2}^2+3\right) \cos \theta}{{k_2}^2+1}\right]\hfill \end{array} $$

(75)

$$ \begin{array}{l}{T}_{19}\left(\theta \right)=\frac{h- b}{k_2}\left[{ \cos}^2\theta +\frac{2\left({k}_2 \sin \theta \cos \theta -{ \cos}^2\theta +{ \sin}^2\theta \right)}{{k_2}^2+4}\right]+\frac{r}{k_2}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{3 r}{k_2\left({k_2}^2+9\right)}\left[{k}_2 \sin \theta { \cos}^2\theta +3{ \sin}^2\theta \cos \theta +\frac{2{k}_2 \sin \theta -\left({k_2}^2+3\right) \cos \theta}{{k_2}^2+1}\right]\hfill \end{array} $$

(76)

$$ \begin{array}{l}{T}_{20}\left(\theta \right)=\frac{b- h}{k_2}\left[{ \cos}^2\theta -\frac{2\left({k}_2 \sin \theta \cos \theta +{ \cos}^2\theta -{ \sin}^2\theta \right)}{{k_2}^2+4}\right]-\frac{r}{k_2}{ \cos}^3\theta \hfill \\ {}\kern3em +\frac{3 r}{k_2\left({k_2}^2+9\right)}\left[{k}_2 \sin \theta { \cos}^2\theta -3{ \sin}^2\theta \cos \theta +\frac{2{k}_2 \sin \theta +\left({k_2}^2+3\right) \cos \theta}{{k_2}^2+1}\right]\hfill \end{array} $$

(77)

$$ \left\{\begin{array}{l}{R}_{13}=\frac{6 rb\left({k}^2+3\right)}{k\left({k}^2+1\right)\left({k}^2+9\right)},{R}_{14}=\frac{b^2}{2 k\left({k}^2+4\right)}\\ {}{R}_{15}=\frac{b^2\left({k}^2+2\right)}{k\left({k}^2+4\right)}-\frac{3{r}^2\left({k}^2+3\right)}{k\left({k}^2+1\right)\left({k}^2+9\right)}\\ {}{R}_{16}=\frac{-2 rb}{k}\left(\frac{2}{k^2+4}+\frac{9}{k^2+9}\right),{R}_{17}=\frac{-4 rb\left({k}^2+3\right)}{k\left({k}^2+4\right)}\\ {}{R}_{18}=\frac{9{r}^2}{8 k\left({k}^2+9\right)},{R}_{19}=\frac{r^2}{8 k}\end{array}\right. $$

(78)

$$ \left\{\begin{array}{l}{I}_{13}=\left( \sin {\theta}_I- \sin {\theta}_E\right)-\frac{1}{3}\left({ \sin}^3{\theta}_I-{ \sin}^3{\theta}_E\right)\\ {}{I}_{14}=\left({\theta}_I-{\theta}_E\right)-\frac{1}{4}\left( \sin 4{\theta}_I- \sin 4{\theta}_E\right)\\ {}{I}_{15}=\frac{3}{4}\left({\theta}_I-{\theta}_E\right)+\frac{1}{2}\left( \sin 2{\theta}_I- \sin 2{\theta}_E\right)+\frac{1}{16}\left( \sin 4{\theta}_I- \sin 4{\theta}_E\right)\\ {}{I}_{16}=\frac{1}{3}\left({ \sin}^3{\theta}_I-{ \sin}^3{\theta}_E\right)-\frac{1}{5}\left({ \sin}^5{\theta}_I-{ \sin}^5{\theta}_E\right)\\ {}{I}_{17}=\frac{1}{5}\left({ \sin}^5{\theta}_I-{ \sin}^5{\theta}_E\right)-\frac{2}{3}\left({ \sin}^3{\theta}_I-{ \sin}^3{\theta}_E\right)+\left( \sin {\theta}_I- \sin {\theta}_E\right)\\ {}{I}_{18}=\left({\theta}_I-{\theta}_E\right)+\frac{1}{4}\left( \sin 2{\theta}_I- \sin 2{\theta}_E\right)-\frac{1}{4}\left( \sin 4{\theta}_I- \sin 4{\theta}_E\right)-\frac{1}{12}\left( \sin 6{\theta}_I- \sin 6{\theta}_E\right)\\ {}{I}_{19}=5\left({\theta}_I-{\theta}_E\right)+\frac{15}{4}\left( \sin 2{\theta}_I- \sin 2{\theta}_E\right)+\frac{3}{4}\left( \sin 4{\theta}_I- \sin 4{\theta}_E\right)+\frac{1}{12}\left( \sin 6{\theta}_I- \sin 6{\theta}_E\right)\end{array}\right. $$

(79)

$$ \left\{\begin{array}{l}{R}_{20}=-\frac{4 kr \tan \beta \left( a \tan \beta - b\right)}{3\left({k}^2+1\right)\left({k}^2+9\right)},{R}_{21}=\frac{6 r\left({k}^2+3\right)\left( a \tan \beta - b\right)}{k\left({k}^2+1\right)\left({k}^2+9\right)}\\ {}{R}_{22}=\frac{{\left( a \tan \beta - b\right)}^2}{k\left({k}^2+4\right)}+\frac{{k r}^2{ \tan}^2\beta}{\left({k}^2+1\right)\left({k}^2+9\right)},{R}_{23}=\frac{r^2 \tan \beta}{2 k\left({k}^2+1\right)}\\ {}{R}_{24}=\frac{\left({k}^2+2\right){\left( a \tan \beta - b\right)}^2}{k\left({k}^2+4\right)}-\frac{3{r}^2\left({k}^2+3\right)}{k\left({k}^2+1\right)\left({k}^2+9\right)}\\ {}{R}_{25}=\frac{4 r \tan \beta \left( a \tan \beta - b\right)}{k\left({k}^2+4\right)},{R}_{26}=\frac{2 r\left( a \tan \beta - b\right)}{k}\left(\frac{2}{k^2+4}+\frac{9}{k^2+9}\right)\\ {}{R}_{27}=-\frac{2 r\left(2{k}^2+3\right)\left({k}^2+6\right) \tan \beta \left( a \tan \beta - b\right)}{5 k\left({k}^2+4\right)\left({k}^2+9\right)}\\ {}{R}_{28}=\frac{4 r\left({k}^2+3\right)\left( a \tan \beta - b\right)}{k\left({k}^2+4\right)},{R}_{29}=\frac{3{r}^2 \tan \beta}{k\left({k}^2+9\right)}\\ {}{R}_{30}=\frac{9{r}^2}{8 k\left({k}^2+9\right)}+\frac{{k r}^2{ \tan}^2\beta}{8\left({k}^2+9\right)},{R}_{31}=-\frac{r^2\left(2{k}^2+9\right) \tan \beta}{3 k\left({k}^2+9\right)},{R}_{32}=\frac{r^2}{8 k}\end{array}\right. $$

(80)

$$ \left\{\begin{array}{l}{I}_{20}={ \cos}^3{\theta}_H-{ \cos}^3{\theta}_I,{I}_{21}=\frac{1}{3}\left({ \sin}^3{\theta}_H-{ \sin}^3{\theta}_I\right)-\left( \sin {\theta}_H- \sin {\theta}_I\right)\\ {}{I}_{22}=\frac{1}{2}\left({\theta}_H-{\theta}_I\right)-\frac{1}{8}\left( \sin 4{\theta}_H- \sin 4{\theta}_I\right),{I}_{23}={ \cos}^4{\theta}_H-{ \cos}^4{\theta}_I\\ {}{I}_{24}=\frac{3}{4}\left({\theta}_H-{\theta}_I\right)+\frac{1}{2}\left( \sin 2{\theta}_H- \sin 2{\theta}_I\right)+\frac{1}{16}\left( \sin 4{\theta}_H- \sin 4{\theta}_I\right)\\ {}{I}_{25}=\frac{1}{5}\left({ \cos}^5{\theta}_H-{ \cos}^5{\theta}_I\right)-\frac{1}{3}\left({ \cos}^3{\theta}_H-{ \cos}^3{\theta}_I\right)\\ {}{I}_{26}=\frac{1}{3}\left({ \sin}^3{\theta}_H-{ \sin}^3{\theta}_I\right)-\frac{1}{5}\left({ \sin}^5{\theta}_H-{ \sin}^5{\theta}_I\right),{I}_{27}={ \cos}^5{\theta}_H-{ \cos}^5{\theta}_I\\ {}{I}_{28}=\frac{1}{5}\left({ \sin}^5{\theta}_H-{ \sin}^5{\theta}_I\right)-\frac{2}{3}\left({ \sin}^3{\theta}_H-{ \sin}^3{\theta}_I\right)+\left( \sin {\theta}_H- \sin {\theta}_I\right)\\ {}{I}_{29}=\frac{3}{2}\left({ \sin}^4{\theta}_H-{ \sin}^4{\theta}_I\right)-\left({ \sin}^6{\theta}_H-{ \sin}^6{\theta}_I\right)\\ {}{I}_{30}=\left({\theta}_H-{\theta}_I\right)+\frac{1}{4}\left( \sin 2{\theta}_H- \sin 2{\theta}_I\right)-\frac{1}{4}\left( \sin 4{\theta}_H- \sin 4{\theta}_I\right)-\frac{1}{12}\left( \sin 6{\theta}_H- \sin 6{\theta}_I\right)\\ {}{I}_{31}={ \cos}^6{\theta}_H-{ \cos}^6{\theta}_I\\ {}{I}_{32}=5\left({\theta}_H-{\theta}_I\right)+\frac{15}{4}\left( \sin 2{\theta}_H- \sin 2{\theta}_I\right)+\frac{3}{4}\left( \sin 4{\theta}_H- \sin 4{\theta}_I\right)+\frac{1}{12}\left( \sin 6{\theta}_H- \sin 6{\theta}_I\right)\end{array}\right. $$

(81)

$$ \left\{\begin{array}{l}{R}_{33}=\frac{6 r\left({k}^2+3\right)\left( h- b\right)}{k\left({k}^2+1\right)\left({k}^2+9\right)},{R}_{34}=\frac{{\left( h- b\right)}^2}{2 k\left({k}^2+4\right)}\\ {}{R}_{35}=\frac{\left({k}^2+2\right){\left( h- b\right)}^2}{k\left({k}^2+4\right)}-\frac{3{r}^2\left({k}^2+3\right)}{k\left({k}^2+1\right)\left({k}^2+9\right)}\\ {}{R}_{36}=\frac{2 r\left( h- b\right)}{k}\left(\frac{2}{k^2+4}+\frac{9}{k^2+9}\right),{R}_{37}=\frac{4 r\left({k}^2+3\right)\left( h- b\right)}{k\left({k}^2+4\right)}\\ {}{R}_{38}=\frac{9{r}^2}{8 k\left({k}^2+9\right)},{R}_{39}=\frac{r^2}{8 k}\end{array}\right. $$

(82)

$$ \left\{\begin{array}{l}{I}_{33}=\frac{1}{3}\left({ \sin}^3{\theta}_B-{ \sin}^3{\theta}_H\right)-\left( \sin {\theta}_B- \sin {\theta}_H\right),{I}_{34}=\left({\theta}_B-{\theta}_H\right)-\frac{1}{4}\left( \sin 4{\theta}_B- \sin 4{\theta}_H\right)\\ {}{I}_{35}=\frac{3}{4}\left({\theta}_B-{\theta}_H\right)+\frac{1}{2}\left( \sin 2{\theta}_B- \sin 2{\theta}_H\right)+\frac{1}{16}\left( \sin 4{\theta}_B- \sin 4{\theta}_H\right)\ \\ {}{I}_{36}=\frac{1}{3}\left({ \sin}^3{\theta}_B-{ \sin}^3{\theta}_H\right)-\frac{1}{5}\left({ \sin}^5{\theta}_B-{ \sin}^5{\theta}_H\right)\\ {}{I}_{37}=\frac{1}{5}\left({ \sin}^5{\theta}_B-{ \sin}^5{\theta}_H\right)-\frac{2}{3}\left({ \sin}^3{\theta}_B-{ \sin}^3{\theta}_H\right)+\left( \sin {\theta}_B- \sin {\theta}_H\right)\\ {}{I}_{38}=\left({\theta}_B-{\theta}_H\right)+\frac{1}{4}\left( \sin 2{\theta}_B- \sin 2{\theta}_H\right)-\frac{1}{4}\left( \sin 4{\theta}_B- \sin 4{\theta}_H\right)-\frac{1}{12}\left( \sin 6{\theta}_B- \sin 6{\theta}_H\right)\\ {}{I}_{39}=5\left({\theta}_B-{\theta}_H\right)+\frac{15}{4}\left( \sin 2{\theta}_B- \sin 2{\theta}_H\right)+\frac{3}{4}\left( \sin 4{\theta}_B- \sin 4{\theta}_H\right)+\frac{1}{12}\left( \sin 6{\theta}_B- \sin 6{\theta}_H\right)\end{array}\right. $$

(83)