1 Introduction

Optical coherence tomography based on low-coherence interference (LCI) has been applied in a wide range of fields from medical to industrial. LCI can measure the path length distribution of scattered or reflected light from an object using a coherence gate. There are three types of LCI: time-domain LCI (TD-LCI), swept-source LCI (SS-LCI), and spectral-domain LCI (SD-LCI) [1, 2]. TD-LCI is not suitable for high-repetition-rate operation because it is necessary to use a mechanical actuator. SD-LCI and SS-LCI can operate at high repetition rates, typically several hundred kHz, but their repetition rates are limited by the sweep frequency of the light source in SS-LCI and by the acquisition rate of the spectrometer in SD-LCI.

On the other hand, time-stretch dispersive Fourier transformation (TS-DFT) has been studied, and this technique is capable of high-repetition-rate measurements above 1 MHz [3, 4]. TS-DFT is a spectroscopic technique for ultra-short pulses of light and measure the temporal profile of a time-stretched laser pulse by traveling through a dispersive medium such as an optical fiber. Since this technique can measure the spectrum of a single laser pulse, its repetition rate is equal to the repetition rate of the ultrashort-pulse laser, which is a type of broadband light source.

Recently, LCI with TS-DFT has been studied [5, 6]. For this method, it is important to measure the group delay and chirp rate for converting from a temporal waveform to a spectrum. In Ref. 5, the group velocity dispersion is measured by expensive equipment, such as an optical spectrum analyzer before measuring the sample, and then the wavelength is calibrated. LCI with TS-DFT measures not only a spectrum but also a spectral interferogram. In Ref. [6], one interferogram was used for calibrating and compensating for the nonlinearity of the chirp rate. There is a possibility of achieving a simpler calibration method by analyzing the spectral interferogram, similar to SD-LCI [7, 8].

In this paper, we developed a 10 MHz repetition-rate LCI system using TS-DFT, and we evaluated its basic characteristics. As a result, the nonlinearity of the chirp rate caused the degradation of the sensitivity and resolution of LCI. We proposed a simple method for calibrating and compensating for the nonlinearity of the chirp rate using interferograms for multiple path length. Thereby, the accuracy in determination nonlinearity of the chirp rate is improved. With this method, the characteristics of the developed system were improved.

2 Principle of LCI with TS-DFT and experimental setup

First, we explain the principle of TS-DFT. Figure 1 shows a schematic diagram of TS-DFT. When ultrashort pulses pass through an optical fiber, the temporal waveform of the laser pulses changes stretched due to the influence of chromatic dispersion while the pulses propagate in optical fiber. The dispersion coefficient of the optical fiber is expressed as

$$ \beta = \beta_{0} + \beta_{1} \varOmega + \frac{1}{2}\beta_{2} \varOmega^{2} + \cdots , $$
(1)

where \( \varOmega = \omega - \omega_{0} \), \( \omega_{0} \) is central angular frequency, \( \beta_{0} \) is group refractive index, \( \beta_{1} \) is group delay, \( \beta_{2} \) is group velocity dispersion. The electric field after propagation over distance z in the optical fiber is expressed as

$$ E\left( {z,t} \right) = \frac{1}{2\pi }\mathop \int \limits_{ - \infty }^{ + \infty } \tilde{E}\left( {0,\omega } \right)\exp \left[ {i\left( {\omega t - \beta z} \right)} \right]{\text{d}}\omega , $$
(2)

where \( \tilde{E} \) is complex number at z = 0, that is, the spectrum of the incident ultra-short pulse. In the case of sufficiently large dispersion, the electric field of the light is approximated as

$$ E\left( {z,t} \right) = \frac{1}{2\pi }\exp \left[ {i\left( {\omega_{0} T + \frac{{T^{2} }}{{2\beta_{2} z}}} \right)} \right]\tilde{E}\left( {0,\frac{T}{{\beta_{2} z}}} \right), , $$
(3)

and the ultra-short pulse is changed to a chirped pulse with a chirp rate of \( 1/\beta_{2} z \). Here, T is the shifted time by the propagation in the optical fiber and \( T = t - \beta_{1} z. \) The temporal profile is similar to the spectrum.

Fig. 1
figure 1

Schematic diagram of TS-DFT

Full size image

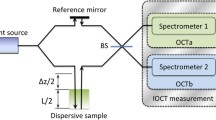
Figure 2 shows the principle of LCI with TS-DFT. The experimental system consists of an ultra-short pulse laser, a large-dispersion optical fiber, a 50:50 optical fiber coupler, a reference mirror, a signal mirror, a photodiode and oscilloscope. The electric fields of the reference light, Er, and the signal light, Es, at the optical detector are, respectively expressed as

$$ E_{\text{r}} \left( t \right) = E_{\text{r0}} \exp \left[ {i\left( {\omega_{0} T_{\text{r}} + \frac{{T_{\text{r}}^{2} }}{{2\beta_{2} z}}} \right)} \right]\tilde{E}\left( {0,\frac{{T_{\text{r}} }}{{\beta_{2} z}}} \right) $$
(4)

and

$$ E_{\text{s}} \left( t \right) = E_{\text{s0}} \exp \left[ {i\left( {\omega_{0} T_{\text{s}} + \frac{{T_{\text{s}}^{2} }}{{2\beta_{2} z}}} \right)} \right]\tilde{E}\left( {0,\frac{{T_{\text{s}} }}{{\beta_{2} z}}} \right) , $$
(5)

where \( T_{\text{r}} \; {\text{is}}\;{\text{the}}\;{\text{time}}\;{\text{of}}\;{\text{reference}}\;{\text{light}}, \;T_{\text{s}} \) is the time of signal light, the relationship between \( T_{\text{r}} \) and \( T_{\text{s}} \) is \( T_{\text{s}} = T_{\text{r}} - \Delta l/c \).

Fig. 2
figure 2

Experimental setup of LCI with TS-DFT

Full size image

\( \Delta l \) is the path length difference between the reference and signal light, and \( c \) is the speed of light. \( E_{\text{r0}} \) is the amplitude of reference light, \( E_{\text{s0}} \) is the amplitude of signal light. These light components interfere at the detector, and the intensity, I, is expressed as

$$ \begin{aligned} I\left( t \right) & = \left[ {E_{\text{r}} \left( t \right) + E_{\text{s}} \left( t \right)} \right]\left[ {E_{\text{r}} \left( t \right) + E_{\text{s}} \left( t \right)} \right]^{*} \\ & = \left( {E_{\text{r0}}^{2} + E_{\text{s0}}^{2} } \right)S\left( {T_{\text{r}} } \right) + 2E_{\text{r0}} E_{\text{s0}} S\left( {T_{\text{r}} } \right)Re\left\{ {\exp \left[ {i\left( {\frac{\Delta l}{{c\beta_{2} z}}T_{\text{r}} - \frac{{\Delta l^{2} }}{{2c^{2} \beta_{2} z}} + \omega_{0} \frac{\Delta l}{c}} \right)} \right]} \right\}, \\ \end{aligned} $$
(6)

where S is the power spectrum. In Eq. 6, we assumed\( {\text{S}}\left( {T_{\text{r}} } \right) = \left| {\tilde{E}\left( {0,\frac{{T_{\text{r}} }}{{\beta_{2} z}}} \right)} \right|^{2} \cong \left| {\tilde{E}\left( {0,\frac{{T_{\text{s}} }}{{\beta_{2} z}}} \right)} \right|^{2} \cong \tilde{E}\left( {0,\frac{{T_{\text{r}} }}{{\beta_{2} z}}} \right)\tilde{E}^{*} \left( {0,\frac{{T_{\text{s}} }}{{\beta_{2} z}}} \right) \cong \tilde{E}^{*} \left( {0,\frac{{T_{\text{r}} }}{{\beta_{2} z}}} \right)\tilde{E}\left( {0,\frac{{T_{\text{s}} }}{{\beta_{2} z}}} \right) \) because the time difference between reference and signal light is sufficiently smaller compared to the pulse width. The interference signal oscillates sinusoidally in time. The beat frequency is \( \Delta l/\beta_{2} z \) and is proportional to the path length, \( \Delta l \), and the chirp rate of the optical fiber, \( 1/\beta_{2} z \).

Here we explain the relation of the measurement range, resolution and repetition rate in LCI with TS-DFT. The measurement range is proportional to the bandwidth of the detectors and the chirp rate. The resolution is inversely proportional to the wavelength bandwidth of the light source. To achieve high resolution and wide measurement range, we need a light source with wide bandwidth and a time-stretcher with large chirp rate. However, the repetition rate must be chosen so that the chirped pulses do not overlap each other. We have set the center wavelength of 1550 nm, 100 nm wavelength bandwidth, 10 MHz repetition rate, and chirp rate of 1000 ps/nm as a goal of our system. For example, using a real-time oscilloscope with 16 GHz bandwidth, the measurement resolution and range are 10.6 μm and 38.4 mm, respectively.

Next, we explain the experimental system. A schematic diagram of the measurement system is shown in Fig. 2. The ultra-short pulse laser was a mode-locked laser diode with a repetition rate of 10 GHz, a wavelength of 1550 nm, and a pulse width below 1 ps. The laser pulse was amplified by an erbium-doped fiber amplifier. The bandwidth was expanded due to the nonlinear effect experienced when passing through a dispersion flat fiber. The repetition rate of 10 GHz was down-converted to 10 MHz by a LiNbO3 modulator. We prepared an ultrashort-pulse laser with a repetition rate of 10 MHz, a bandwidth of 20 nm from 1547 to 1567 nm, and a pulse width below 1 ps. This laser pulse was entered into a dispersion compensation fiber (DCF) with a length of 8.47 km, and the pulse width was stretched to 28 ns. Then the stretched pulse entered a fiber-optic Michelson interferometer. The interferometer consisted of a 50:50 optical fiber coupler, a reference mirror, a signal mirror, two collimator lenses, and an objective lens. The reference mirror of the interference system was mounted on a linear stage, and the path length could be adjusted with an accuracy of \( 20\;\upmu \) m in the range of 0–0.016 m. The optical signal was detected by a photodiode (PD: Agilent 83440B bandwidth DC-6 GHz) and recorded by a real-time oscilloscope (Tektronix DSA71604 16 GHz 50GS/s).

3 Basic characteristics of the developed system

Figure 3a and b show the 10 MHz interference signals recorded by the real-time oscilloscope. The horizontal axis is time and the vertical axis is signal intensity. The path length, \( \Delta l \), was set to 0.002 m by adjusting the reference mirror. The time range in Fig. 3a is from 0 to 2000 ns, and that in Fig. 3b shows the detail of one of these pulses. From Fig. 3a, it was confirmed that a pulse train was acquired at intervals of 100 ns. This means that all pulses at the 10 MHz repetition rate can be measured. From Fig. 3b, the interference signal is clearly observed. We confirm the interference fringe shown in Fig. 3b is stable, thought the envelope in Fig. 3a is unstable because each pulse shape changes in time. The developed system could measure the interference signal at a 10 MHz repetition rate.

Fig. 3
figure 3

Temporal waveform of interference signal. a Temporal range from 0 to 2000 ns. b A detail of temporal range from 1700 to 1800 ns

Full size image

Next, we show the path length difference estimated from measured interference signal. We obtained the beat frequency by taking the Fourier transformation of the interference signal. The path length difference was equal to the beat frequency divided by the chirp rate. Chirp rate was estimated to be 10,487 ps2 at the center wavelength of 1557 nm using the chromatic dispersion value of the DCF, namely, 1296 ps/nm.

Figure 4 shows the Fourier transform of the interference signals for \( \Delta l = \) 0.002 to 0.016 m. The horizontal axis represents the measured path length difference. The peak level of intensity indicates the measurement sensitivity, and full width at half maximum (FWHM) indicates the measurement resolution. From Fig. 4, it is clear that the peak positions of the Fourier transform almost agreed with the set path length difference. However, as \( \Delta l \) increased, the sensitivity decreased and the resolution degraded. We considered that the reason for this degradation was the nonlinearity of the chirp rate [5].

Fig. 4
figure 4

Fourier transform of interference signal

Full size image

4 Improvement of FFT signal characteristics

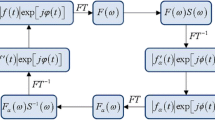
In this section, we discuss the improvement of the Fourier transform signal. In Eq. 6, we assumed that the chirp rate is linear. Taking the nonlinearity of the chirp rate into consideration, the intensity of the detected light is modified to

$$ I = \exp \left\{ {i\left[ {\left( {a_{1} \Delta l - b_{1} } \right)T + \left( {a_{2} \Delta l - b_{2} } \right)T^{2} } \right]} \right\}. $$
(7)

In this equation, we assume second-order chromatic dispersion and ignore the constant phase. Here, \( a_{1} {\text{and }}b_{1} \) are constants related to the beat frequency, \( a_{2} {\text{and }}b_{2} \) are constants related to the chirp of the beat frequency, where \( a_{1} {\text{and }}a_{2} \) are proportional to \( \Delta l \), and \( b_{1} {\text{and }}b_{2} \) are independent of \( \Delta l \). We can calculate the phase of the interference signal using a Hilbert transform

$$ \varphi = \left( {a_{1} \Delta l - b_{1} } \right)T + \left( {a_{2} \Delta l - b_{2} } \right)T^{2} \equiv B_{1} T + B_{2} T^{2} . $$
(8)

Figure 5 shows \( B_{1} {\text{and }}B_{2} \) which were obtained by polynomial fitting of the phase calculated using the Hilbert transform. The horizontal axis is the path length difference. It is clear that \( B_{1} {\text{and }}B_{2} \) are linear but not proportional. We calculated \( a_{1} = 1929\; {\text{ns}}^{ - 1} \;{\text{m}}^{ - 1} \) and \( a_{2} = 3.686\;{\text{ns}}^{ - 2} \;{\text{m}}^{ - 1} \) from the slope then \( b_{1} \; {\text{and}}\;b_{2} \) are not zero. It can be seen that the compensation is more accurate by evaluating from the gradients for multi path length.

Fig. 5
figure 5

Variation of the coefficients of the formula. a A graph plotted B1 against Δl. b A graph plotted B2 against Δl. In both graphs, filled circles and dotted lines represent measured values and linear approximations, respectively

Full size image

On the other hand, in terms of wave number \( k = 1/\lambda \), the intensity of the detected light is generally expressed by

$$ I = \exp \left\{ {i\left( {2\pi \Delta lk} \right)} \right\}. $$
(9)

Comparing Eq. 7 and Eq. 9, the relationship between wave number, k, and time, T, is

$$ k = \frac{{a_{1} }}{2\pi }T + \frac{{a_{2} }}{2\pi }T^{2} . $$
(10)

Using Eq. 10 we can covert the temporal axis of the measured interference signal to the k axis. Consequently, we can compensate for the chirp of the beat frequency. However, the sampling interval in wave number k is not constant. To execute the Fourier transformation, the wave number k has to be resampled so that the sampling interval is constant.

Figure 6 shows the Fourier transform of the interference signals after compensation of the nonlinearity of the chirp rate. It was confirmed that the sensitivity and the resolution was improved. We also confirmed that the maximum error of the measured path length was below 0.07 mm that was smaller than the resolution of measurement. Figures 7 show the comparison of (a) the sensitivity and (b) the resolution before and after compensation. From Fig. 7a, it was clear that the sensitivity was improved from 0.37 to 0.74 when \( \Delta l \) is 0.016 m. From Fig. 7b, it was clear that the resolution has improved from 0.90 mm to 0.15 mm when \( \Delta l \) is 0.016 m. Therefore, we greatly improved the degradation of the sensitivity and resolution by compensating for the nonlinearity of the chirp rate.

Fig. 6
figure 6

Fourier transform of interference signal

Full size image
Fig. 7
figure 7

Comparison of signal quality of Fourier transform. a A relationship between Δl and relative peak value of FFT. b A relationship between Δl and FWHM of FFT

Full size image

5 Conclusion

In the work, described in this paper, we developed an LCI measurement system using the TS-DFT technique and demonstrated 10 MHz measurement of an interference signal. The nonlinearity of the chirp rate affected the sensitivity and resolution of the measurement in this method. We proposed a novel and simple method for calibrating and compensating for the nonlinearity of the chirp rate using interferograms for multiple path length. With this method, the degradation of the sensitivity and resolution of the system was improved.