Skip to main content
SpringerLink
Log in

Fabric characterisation in transitional soils

  • Original Paper
  • Published:
Granular Matter Aims and scope Submit manuscript

Abstract

A “transitional” mode of soil behaviour implies that dense and loose samples do not converge towards the same volumes within the strains and stresses applied by simple oedometer and triaxial tests. As this behaviour involves soils with different gradings and mineralogies (e.g. gap graded, well graded and/or mixed mineralogies), identifying the factors responsible is difficult. Nevertheless, it has been previously speculated that strong forms of fabric that are difficult to break down as strains and stresses are applied, might be the common cause. This paper aims at investigating some elements of fabric at the microscale of transitional soils. A gap graded and two well graded mixtures with large amounts of non-plastic fines were investigated by oedometer and triaxial tests. As it would be difficult to identify experimentally many commonly used elements of fabric in these soils, e.g. the contact network, mercury intrusion porosimetry was used as a first step to characterise the evolution of pore size distributions (PSDs) of dense and loose samples undergoing the same stress paths, using the PSDs as a proxy of fabric. Multi-directional bender element testing was performed to confirm the isotropy of the elastic stiffness, from which it might be inferred that the fabric is also isotropic. Statistical parameters of the PSDs were calculated, the changes of which were related to the evolution of macroscale void ratios. The robust fabrics causing lack of convergence were characterised by a complex evolution of the PSDs, the initial differences of which could not be erased during conventional testing. This work also provided a simple method to examine the fabric of particularly well graded or gap graded materials, for which other techniques, such as CT or SEM, could not reveal the multi-scale nature of the fabric.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Abbreviations

G:

Elastic shear modulus

\(\hbox {G}_{\mathrm{hh}}\) :

Shear modulus calculated from horizontally propagated, horizontally polarised shear waves

\(\hbox {G}_{\mathrm{hv}}\) :

Shear modulus calculated from horizontally propagated, vertically polarised shear waves

\(\hbox {G}_{\mathrm{vh}}\) :

Shear modulus calculated from vertically propagated, horizontally polarised shear waves

LBS:

Leighton Buzzard sand

LMS:

Crushed limestone

PSD:

Pore size distribution

SPF:

Sand plastic fines (75% sand–25% kaolin)

\({\upgamma }\) :

Skewness of PSD

\({\upkappa }\) :

Kurtosis of PSD

\(\upmu \) :

Mean of PSD

\(\upsigma \) :

Standard deviation of PSD

References

  1. Coop, M.R.: Limitations of a Critical State framework applied to the behaviour of natural and “transitional” soils. In: Proceedings of 6th International Symposium on Deformation Characteristics of Geomaterials, IS-Buenos Aires, pp. 115–155 (2015)

  2. Ferreira, P.M., Bica, A.V.D.: Problems in identifying the effects of structure and critical state in a soil with a transitional behaviour. Géotechnique 56(7), 445–454 (2006)

    Article  Google Scholar 

  3. Altuhafi, F.N., Baudet, B.A., Sammonds, P.: The mechanics of subglacial sediment: an example of new "transitional behaviour". Can. Geotech. J. 47(7), 775–790 (2010)

    Article  Google Scholar 

  4. Coop, M.R., Cotecchia, F.: The compression of sediments at the archaeological site of Sibari. In: Proceedings of 11th ECSMFE-Copenhagen, vol. 1, pp. 19–26 (1995)

  5. Cotecchia, F., Chandler, R.J.: One-dimensional compression of a natural clay: structural changes and mechanical effects. In: Proceedings of the Second International Symposium on Hard Soils–Soft Rocks, Naples, pp. 103–114 (1998)

  6. Fearon, R.E., Coop, M.R.: Reconstitution: what makes an appropriate reference material? Géotechnique 50(4), 471–477 (2000)

    Article  Google Scholar 

  7. Atkinson, J.H., Fookes, P.G., Miglio, B.F., Pettifer, G.S.: Destructuring and disaggregation of Mercia Mudstone during full-face tunnelling. Q. J. Eng. Geol. Hydrogeol. 36(4), 293–303 (2003)

    Article  Google Scholar 

  8. Minh, N.H., Cheng, Y.P.: A DEM investigation of the effect of particle-size distribution on one-dimensional compression. Géotechnique 63(1), 44–53 (2013)

    Article  Google Scholar 

  9. Shipton, B., Coop, M.R.: Transitional behaviour in sands with plastic and non-plastic fines. Soils Found. 55(1), 1–16 (2015)

    Article  Google Scholar 

  10. Oda, M.: Initial fabrics and their relations to mechanical properties of granular material. Soils Found. 12(1), 17–36 (1972)

    Article  Google Scholar 

  11. Kuwano, R., Jardine, R.J.: On the applicability of cross-anisotropic elasticity to granular materials at very small strains. Géotechnique 52(10), 727–749 (2002)

    Article  Google Scholar 

  12. Yang, Z.X., Li, X.S., Yang, J.: Undrained anisotropy and rotational shear in granular soil. Géotechnique 57(4), 371–384 (2007)

    Article  Google Scholar 

  13. Delage, P., Lefebvre, G.: Study on the structure of a sensitive Champlain clay and of its evolution during consolidation. Can. Geotech. J. 21(1), 21–35 (1984)

    Article  Google Scholar 

  14. Carraro, J., Prezzi, M., Salgado, R.: Shear strength and stiffness of sands containing plastic and nonplastic fines. J. Geotech. Geoenviron. Eng. ASCE 135(9), 1167–1178 (2009)

    Article  Google Scholar 

  15. Hattab, M., Fleureau, J.-M.: Experimental study of kaolin particle orientation mechanism. Géotechnique 60(5), 323–332 (2010)

    Article  Google Scholar 

  16. Fonseca, J., O’Sullivan, C., Coop, M.R., Lee, P.D.: Quantifying the evolution of soil fabric during shearing using directional parameters. Géotechnique 63(6), 487–499 (2013)

    Article  Google Scholar 

  17. Fonseca, J., O’Sullivan, C., Coop, M.R., Lee, P.D.: Quantifying the evolution of soil fabric during shearing using scalar parameters. Géotechnique 63(10), 818–829 (2013)

    Article  Google Scholar 

  18. Nocilla, A., Coop, M.R., Colleselli, F.: The mechanics of an Italian silt: an example of “transitional” behaviour. Géotechnique 56(4), 261–271 (2006)

    Article  Google Scholar 

  19. Bruchon, J.-F., Pereira, J.-M., Vandamme, M., Lenoir, N., Delage, P., Bornert, M.: X-ray microtomography characterisation of the changes in statistical homogeneity of an unsaturated sand during imbibition. Géotech. Lett. 3(2), 84–88 (2013)

    Article  Google Scholar 

  20. Todisco, M.C.: Behaviour of non-convergent soils: effect of particle size, mineralogy and fabric. Ph.D. thesis, City University of Hong Kong (2016)

  21. Shipton, B., Coop, M.R.: On the compression behaviour of reconstituted soils. Soils Found. 52(4), 668–681 (2012)

    Article  Google Scholar 

  22. Takahashi, A., Jardine, R.J.: Assessment of standard research sand for laboratory testing. Q. J. Eng. Geol. Hydrogeol. 40(1), 93–103 (2007)

    Article  Google Scholar 

  23. Altuhafi, F.N., Coop, M.R.: Changes to particle characteristics associated with the compression of sands. Géotechnique 61(6), 459–471 (2011)

    Article  Google Scholar 

  24. Ladd, R.S.: Preparing test specimens using undercompaction. Geotech. Test. J. ASTM 14(4), 371–382 (1978)

    Google Scholar 

  25. Atkinson, J.H., Evans, J.S.: Discussion on: The measurement of soil stiffness in the triaxial apparatus, by Jardine, R. J., Symes, N. J. and Burland, J. B. Géotechnique 35(3), 378–382 (1985)

    Article  Google Scholar 

  26. Tatsuoka, F., Ishihara, M., Di Benedetto, H., Reiko, K.: Time-dependent shear deformation characteristics of geomaterials and their simulation. Soils Found. 42(2), 103–129 (2002)

    Article  Google Scholar 

  27. Li, P.Q., Baudet, B.A.: Strain rate dependence of the critical state line of reconstituted clays. Géotech. Lett. 6(1), 66–71 (2016)

    Article  Google Scholar 

  28. Bishop, A.W., Wesley, L.D.: A hydraulic triaxial apparatus for controlled stress path testing. Géotechnique 25(4), 99–112 (1975)

    Article  Google Scholar 

  29. Pennington, D.S., Nash, D.F.T., Lings, M.L.: Anisotropy of G\(_0\) shear stiffness in Gault clay. Géotechnique 47(3), 391–398 (1997)

    Article  Google Scholar 

  30. Abbiss, C.P.: Shear wave measurements of the elasticity of the ground. Géotechnique 31(1), 91–104 (1981)

    Article  Google Scholar 

  31. Washburn, E.W.: The dynamics of capillary flow. Phys. Rev. Lett. 17(3), 273–283 (1921)

    ADS  Google Scholar 

  32. Klock, G.O., Boersma, L., DeBacker, L.W.: Pore size distributions as measured by the mercury intrusion method and their use in predicting permeability. Soil Sci. Soc. Am. Proc. 33(1), 12–15 (1969)

    Article  ADS  Google Scholar 

  33. Diamond, S.: Pore size distribution in clays. Clays Clay Miner. 18, 7–23 (1970)

    Article  ADS  Google Scholar 

  34. Penumadu, D., Dean, J.: Compressibility effect in evaluating the pore-size distribution of kaolin clay using mercury intrusion porosimetry. Can. Geotech. J. 37(2), 393–405 (2000)

    Article  Google Scholar 

  35. Folk, R.L., Ward, W.C.: Brazos River bar: a study in the significance of grain size parameters. J. Sediment. Petrol. 27, 3–26 (1957)

    Article  ADS  Google Scholar 

  36. Pearson, K.: Editorial note to “Inequalities for moments of frequency functions and for various statistical constants”. Biometrika 21(1–4), 361–375 (1929)

  37. Jaky, J.: Pressure in silos. In: Proceedings of 2nd ICSMFE, Rotterdam, vol. 1, pp. 103–107 (1948)

  38. Juang, C.H., Holtz, R.D.: Fabric, pore size distribution, and permeability of sandy soils. J. Geotech. Eng. ASCE 112(9), 855–868 (1986)

    Article  Google Scholar 

  39. Arson, C., Pereira, J.-M.: Influence of damage on pore size distribution and permeability of rocks. Int. J. Numer. Anal. Methods Geomech. 37(8), 810–831 (2013)

    Article  Google Scholar 

  40. Pereira, J.-M., Arson, C.: Retention and permeability properties of damaged porous rocks. Comput. Geotech. 48, 272–82 (2013)

    Article  Google Scholar 

Download references

Acknowledgements

The work described in this paper was fully supported by a grant from the Research Grants Council of the Hong Kong Special Administrative Region, China (project no. CityU 112813). The authors are grateful to Prof. Pierre Delage for his valuable comments on MIP data and Dr. Madhusudhan for carrying out X-Ray CT scans at the University of Southampton. The technician Mr. Xavier Boulay and Baptiste Chabot are acknowledged for their technical support in conducting the MIP tests. Also, we would like to thank the reviewers for their constructive remarks which helped to improve the quality of the paper.

Author information

Authors and Affiliations

  1. Coffey Geotechnics, Atlantic House, Atlas Business Park, Manchester, UK formerly City University of Hong Kong, Hong Kong

    M. C. Todisco

  2. University College London, Chadwick Building, Gower Street, London, UK

    M. R. Coop

  3. Laboratoire Navier, UMR 8205, École des Ponts ParisTech, IFSTTAR, CNRS, Champs-sur-Marne, Paris, France

    J.-M. Pereira

Authors
  1. M. C. Todisco
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. R. Coop
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J.-M. Pereira
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. C. Todisco.

Ethics declarations

Conflict of interest

The authors certify that they have no affiliations with or involvement in any organization or entity with any financial or non-financial interest (such as personal or professional relationships, affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript.

Appendix

Appendix

1.1 Micro X-ray CT imaging

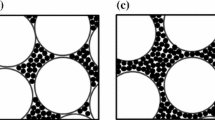
Visually, the micro X-ray CT scan images in Fig. 9 of dense and loose oedometer samples of LBS do not show significant differences in particle arrangement. The images also highlight a key problem for the use of CT to characterise the fabric of these soils. At the scale shown of \(900\,\upmu \hbox {m}\) across the image, there are insufficient larger particles and voids to be statistically reliable, and so much larger images would be needed. However, the sizes of the small particles and voids are already too small to be separated reliably by segmentation using existing methods within the resolution of the images, and this problem would be exacerbated for a larger image. For this reason, MIP testing was preferred.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Todisco, M.C., Coop, M.R. & Pereira, JM. Fabric characterisation in transitional soils. Granular Matter 20, 20 (2018). https://doi.org/10.1007/s10035-018-0786-1

Download citation

  • Received:

  • Published:

  • DOI: https://doi.org/10.1007/s10035-018-0786-1

Keywords

Search

Navigation